4.3相似三角形 课件

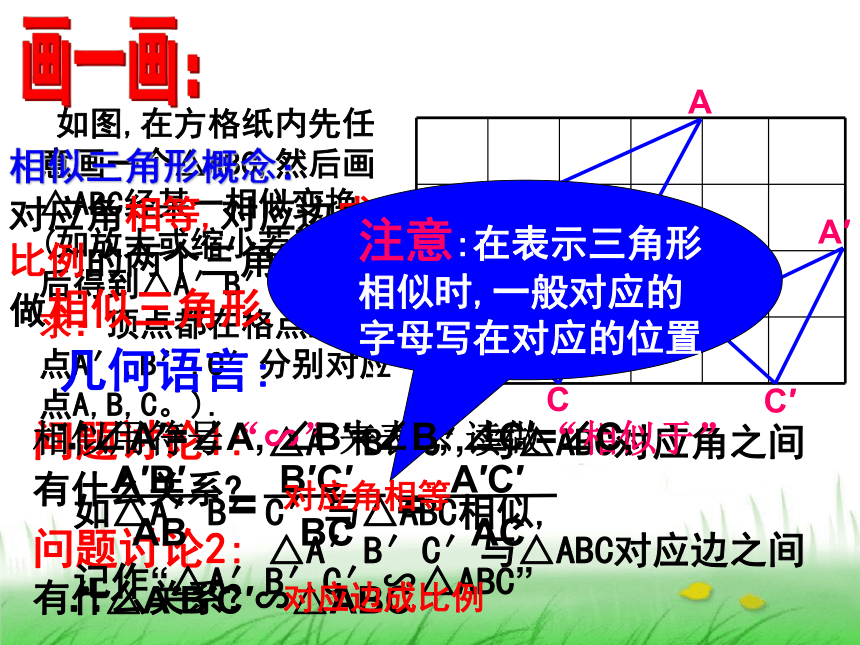
课件12张PPT。浙教版九（上）§第四章4.3相似三角形学科网 学科网 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(要求：顶点都在格点上，点A′,B′,C′分别对应点A,B,C。).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
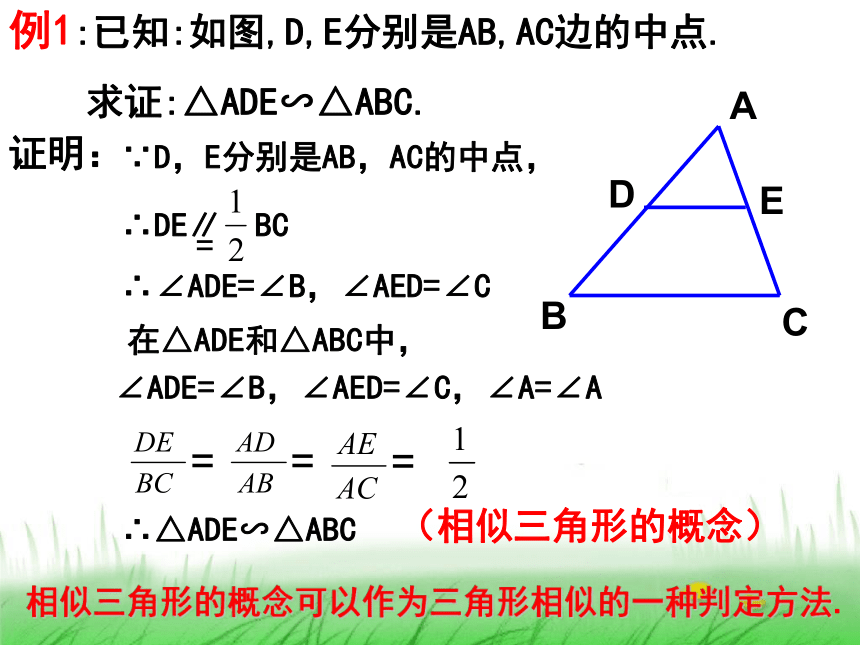
记作“△A′B′C′∽△ABC”几何语言:∴△A′B′C′∽△ABC画一画：相似三角形概念：对应角相等对应边成比例 １、两个全等三角形一定相似吗？为什么？ ２、两个直角三角形一定相似吗？为什么？辩一辩：相似，对应角相等，对应边成比例。不一定相似，有一个锐角相等的直角三角形相似。例1:已知:如图,D,E分别是AB,AC边的中点.
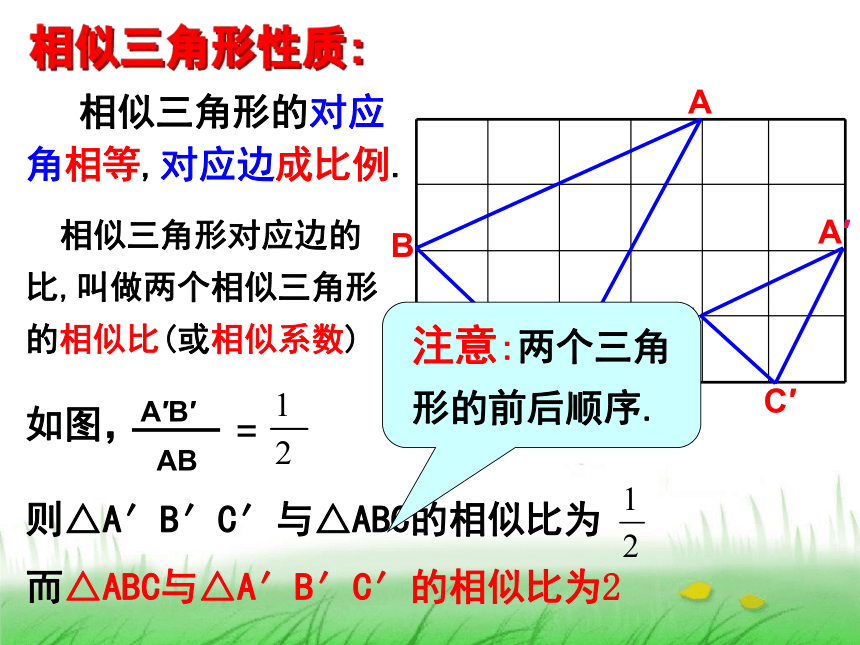
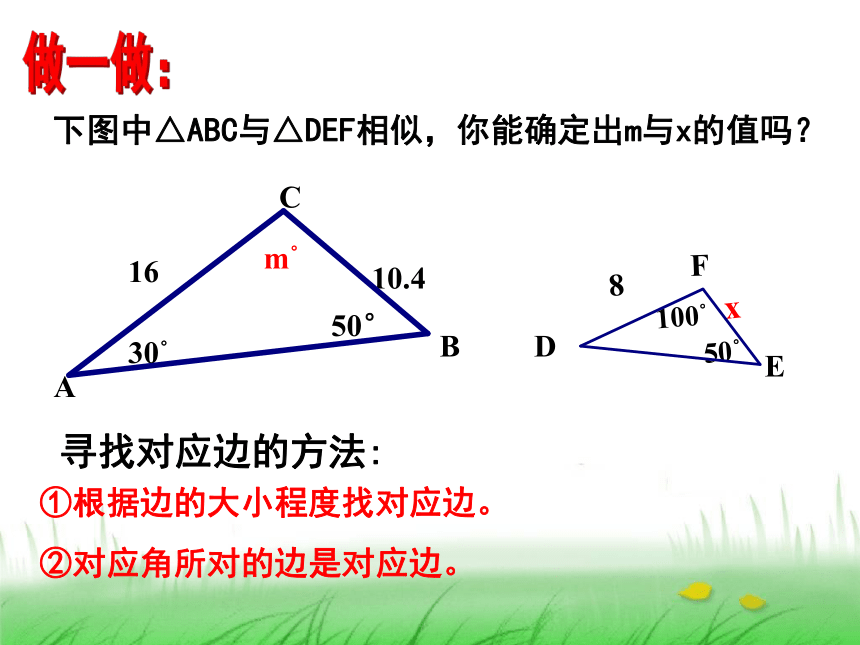
求证:△ADE∽△ABC.证明：∵D，E分别是AB，AC的中点，∴∠ADE=∠B，∠AED=∠C在△ADE和△ABC中，∠ADE=∠B，∠AED=∠C，∠A=∠A∴△ADE∽△ABC（相似三角形的概念）相似三角形的概念可以作为三角形相似的一种判定方法.Zx.xk 相似三角形的对应角相等,对应边成比例. 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数)而△ABC与△A′B′C′的相似比为2相似三角形性质:下图中△ABC与△DEF相似，你能确定出m与x的值吗？做一做：①根据边的大小程度找对应边。
②对应角所对的边是对应边。30°50°1610.4ABCm°寻找对应边的方法:如图,△ADE和△ABC相似,点D和点 B 是对应点。根据以下不同的图形分别说出△ADE与△ABC的对应角和对应边成比例的比例式。找一找：C例2、如图(1),D,E分别是△ABC的边BA、CA延长线上的
点, 点D与点B是对应点.△ADE ∽△ABC.
已知 AD﹕AB=1﹕2,BC=9cm,求DE的长. 变式1：如图(2),D,E分别是△ABC的边AB,AC上的点,点D
与点B是对应点. △ADE ∽△ABC.
已知AD﹕DB=1﹕2,BC=9cm,求DE的长.变式2如图(3),D,E分别是△ABC的AB,AC边上的点，
△ADE∽△ACB.已知∠ADE＝∠C，AD＝2cm,DB＝4cm,AC＝10cm,求AE的长.1.如图，D是AB上的一点。△ABC∽△ACD，且AD：AC＝2：3,
∠ADC= 65°, ∠B＝37 °.
（1）求∠ACB， ∠ACD的度数；
（2）写出△ABC与△ACD的对应边成比例的比例式，求出相似比。 2、如图，AB，CD相交于点0, △AOC∽△BOD 。
（1）如果OC：OD＝1：2,AC＝5,求BD的长；
（2）如果∠A＝35°, ∠AOC＝100°,求∠D的度数。65°37°练一练 小明打算制作两个相似的三角形框架，其中
一个三角形框架的三边长分别为4cm，6cm，9cm。
已知另一个三角形一条边长度为3cm，
则余下的那两条边的长度,你能帮助他确定吗？探究活动:1.概念：对应角相等, 对应边成比例的两个三角形,
叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上！
2.性质：相似三角形的对应角相等, 对应边对应成比例.

几何语言：
∵△ABC∽△DEF,
∴∠A=∠D,∠B=∠E,∠C=∠F.相似比：相似三角形对应边的比谈收获，共分享 相似图形 相似三角形 全等三角形 相似三角形一般特殊特殊一般1.本节课我们用相似三角形的知识解决了
了哪几种类型的题目？2.知识系统性