4.4 2-3相似三角形的判定方法二三 课件
文档属性
| 名称 | 4.4 2-3相似三角形的判定方法二三 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 790.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-15 19:57:16 | ||
图片预览




文档简介
课件19张PPT。4.4 两个三角形相似的判定
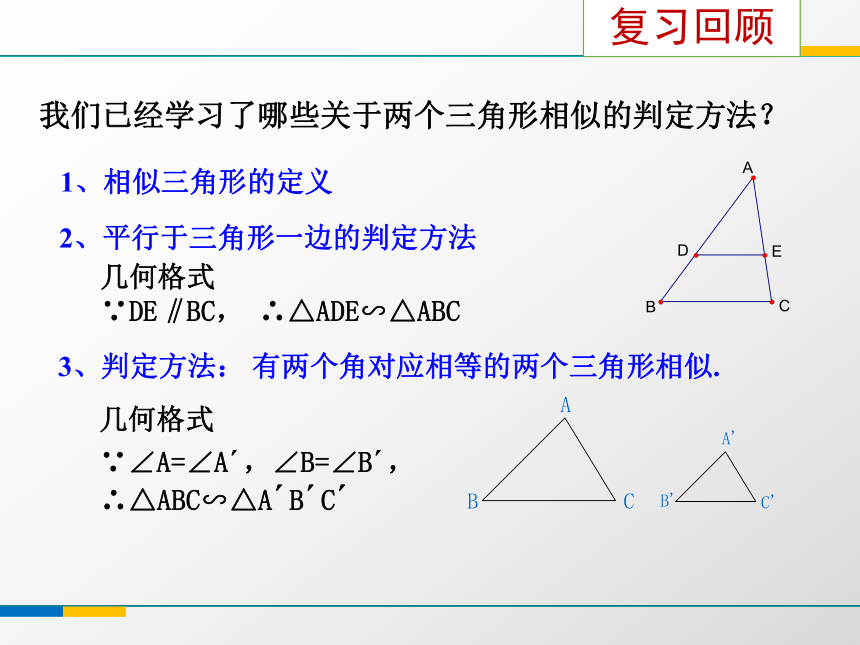
(第2-3课时)我们已经学习了哪些关于两个三角形相似的判定方法?2、平行于三角形一边的判定方法3、判定方法: 有两个角对应相等的两个三角形相似. 几何格式
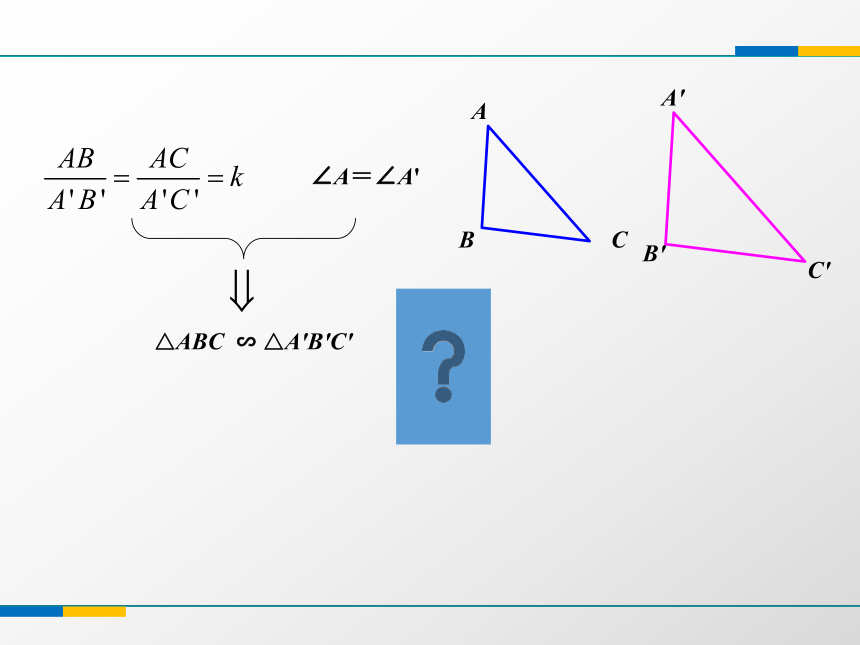
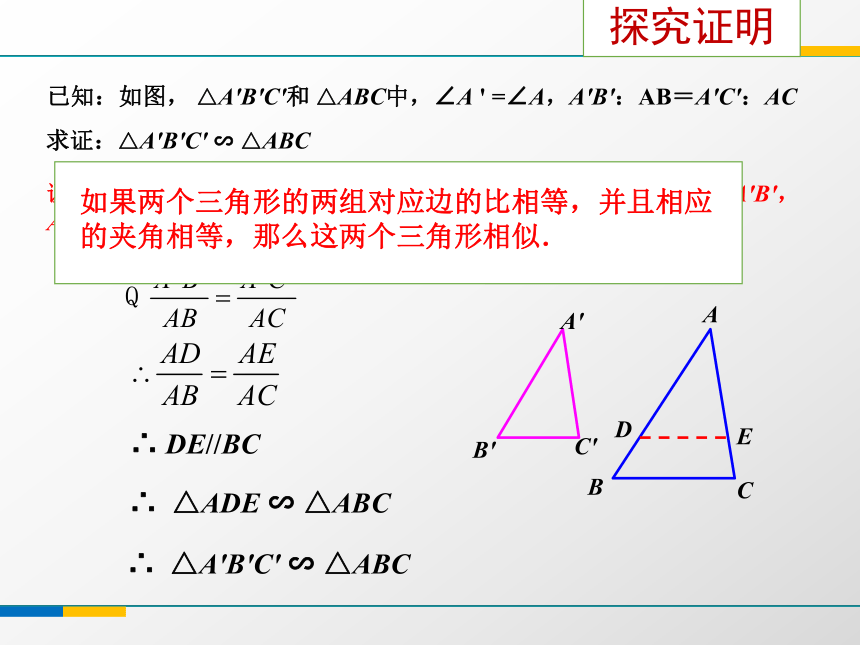
∵DE‖BC, ∴△ADE∽△ABC1、相似三角形的定义复习回顾∠A=∠A'△ABC ∽ △A'B'C'已知:如图, △A'B'C'和 △ABC中,∠A ' =∠A,A'B':AB=A'C':AC求证:△A'B'C' ∽ △ABC 证明:在△ABC 的边AB、AC(或它们的延长线)上别截取AD=A'B',AE=A'C',连结DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE ∴ DE//BC∴ △ADE ∽ △ABC∴ △A'B'C' ∽ △ABC A'B'C'ABCDE探究证明如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.例2 如图,用卡钳测量容器内径的示意图.现量得卡钳上A、D两点的距离为5cm, ,求容器的内径BC. 你能利用刚才所学的知识解决这个问题吗?提示:△AOD ∽ △BOC例题探究1.判 断
(1)有一个锐角相等的两个直角三角形相似.( )
(2)有一个角相等的两个等腰三角形相似.( )
(3)顶角相等的两个等腰三角形相似.( ) √√×课堂练习2.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30解: ∠A=∠A'∴△ABC∽△A'B'C'对于△ABC和△A'B'C',如果 ∠B=∠B',这
两个三角形一定相似吗?试着画画看. 不一定相似A 请任意画一个△ ABC,作△A′B′C′,使△A′B′C′的边长为原来的2倍.相似三角形的判定方法:三边对应成比例的两个三角形相似.问题:△ABC与△A′B′C′
相似吗?合作探究它的几何格式表示如下: ∴△ABC∽ △A′B′C′相似三角形的判定方法:三边对应成比例的两个三角形相似.两个等边三角形一定相似吗?△ABC与△A′B′C′都是等边三角形 是否有△ABC∽△A′B′C′ ?议一议例4 如图判断4×4方格中的两个三角形是否相似,并说明理由. 解:观察图形根据勾股定理我们可以计算出例题探究例5 你能利用本节所学的知识解决这个问题吗?1、下面每组的两个三角形是否相似?请说说你的理由:C⑴⑵ 做一做2、如图, D为⊿ ABC的边AB上一点若要使⊿ACD与⊿ABC相似, 可以添加什么条件? 你有几种添加条件的不同方法?
1. 根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30
(2)AB=10cm,BC=8cm,AC=16cm
A'B' =16cm,B'C' =12.8cm,A'C' =25.6cm解: (1)∠A=∠A'∴△ABC∽△A'B'C'∴△ABC∽△A'B'C'(2)课堂练习2、根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
(2)AB=4cm,BC=6cm,AC=8cm.
'B'=12cm,B'C'=18cm,A'C'=21cm解:(1)∵又 ∠A=∠A'∴ △ABC∽△A'B'C'(2)∵△ABC与△A'B'C'的三组对应边的比不等,它们不相似两三角形的相似比是多少?要使两三角形相似,不改变AC的长,A'C'的长应当改为多少? 两个三角形相似的判定方法:3. 两边对应成比例,且夹角相等的两个三角形相似.4. 三边对应成比例,两三角形相似.2. 有两个角对应相等的两个三角形相似.1. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.课堂小结对比记忆
(第2-3课时)我们已经学习了哪些关于两个三角形相似的判定方法?2、平行于三角形一边的判定方法3、判定方法: 有两个角对应相等的两个三角形相似. 几何格式
∵DE‖BC, ∴△ADE∽△ABC1、相似三角形的定义复习回顾∠A=∠A'△ABC ∽ △A'B'C'已知:如图, △A'B'C'和 △ABC中,∠A ' =∠A,A'B':AB=A'C':AC求证:△A'B'C' ∽ △ABC 证明:在△ABC 的边AB、AC(或它们的延长线)上别截取AD=A'B',AE=A'C',连结DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE ∴ DE//BC∴ △ADE ∽ △ABC∴ △A'B'C' ∽ △ABC A'B'C'ABCDE探究证明如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.例2 如图,用卡钳测量容器内径的示意图.现量得卡钳上A、D两点的距离为5cm, ,求容器的内径BC. 你能利用刚才所学的知识解决这个问题吗?提示:△AOD ∽ △BOC例题探究1.判 断
(1)有一个锐角相等的两个直角三角形相似.( )
(2)有一个角相等的两个等腰三角形相似.( )
(3)顶角相等的两个等腰三角形相似.( ) √√×课堂练习2.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30解: ∠A=∠A'∴△ABC∽△A'B'C'对于△ABC和△A'B'C',如果 ∠B=∠B',这
两个三角形一定相似吗?试着画画看. 不一定相似A 请任意画一个△ ABC,作△A′B′C′,使△A′B′C′的边长为原来的2倍.相似三角形的判定方法:三边对应成比例的两个三角形相似.问题:△ABC与△A′B′C′
相似吗?合作探究它的几何格式表示如下: ∴△ABC∽ △A′B′C′相似三角形的判定方法:三边对应成比例的两个三角形相似.两个等边三角形一定相似吗?△ABC与△A′B′C′都是等边三角形 是否有△ABC∽△A′B′C′ ?议一议例4 如图判断4×4方格中的两个三角形是否相似,并说明理由. 解:观察图形根据勾股定理我们可以计算出例题探究例5 你能利用本节所学的知识解决这个问题吗?1、下面每组的两个三角形是否相似?请说说你的理由:C⑴⑵ 做一做2、如图, D为⊿ ABC的边AB上一点若要使⊿ACD与⊿ABC相似, 可以添加什么条件? 你有几种添加条件的不同方法?
1. 根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30
(2)AB=10cm,BC=8cm,AC=16cm
A'B' =16cm,B'C' =12.8cm,A'C' =25.6cm解: (1)∠A=∠A'∴△ABC∽△A'B'C'∴△ABC∽△A'B'C'(2)课堂练习2、根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
(2)AB=4cm,BC=6cm,AC=8cm.
'B'=12cm,B'C'=18cm,A'C'=21cm解:(1)∵又 ∠A=∠A'∴ △ABC∽△A'B'C'(2)∵△ABC与△A'B'C'的三组对应边的比不等,它们不相似两三角形的相似比是多少?要使两三角形相似,不改变AC的长,A'C'的长应当改为多少? 两个三角形相似的判定方法:3. 两边对应成比例,且夹角相等的两个三角形相似.4. 三边对应成比例,两三角形相似.2. 有两个角对应相等的两个三角形相似.1. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.课堂小结对比记忆
同课章节目录
