4.5三角形中位线 课件

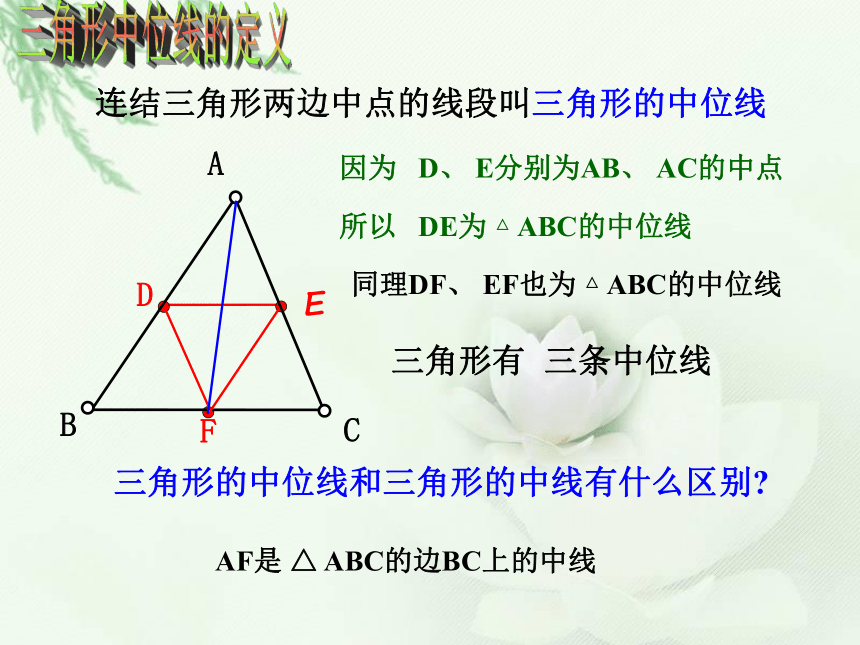
课件12张PPT。4.5三角形中位线三角形中位线的定义连结三角形两边中点的线段叫三角形的中位线三角形有 三条中位线因为 D、 E分别为AB、 AC的中点
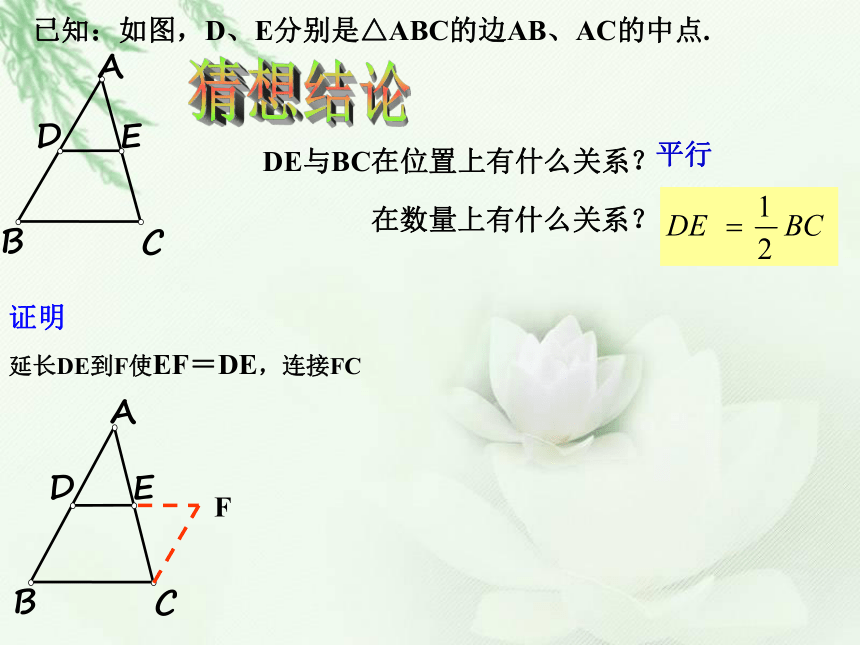
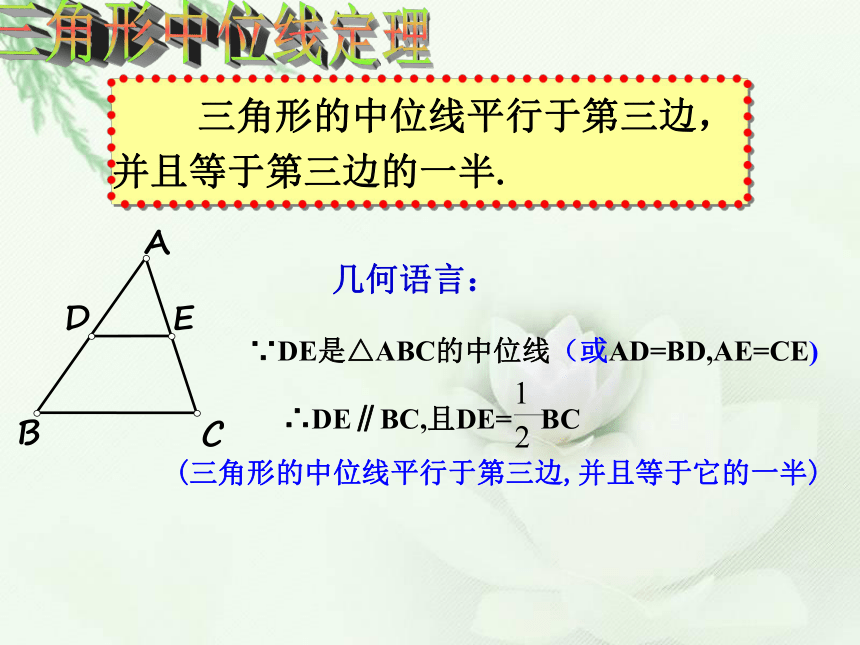
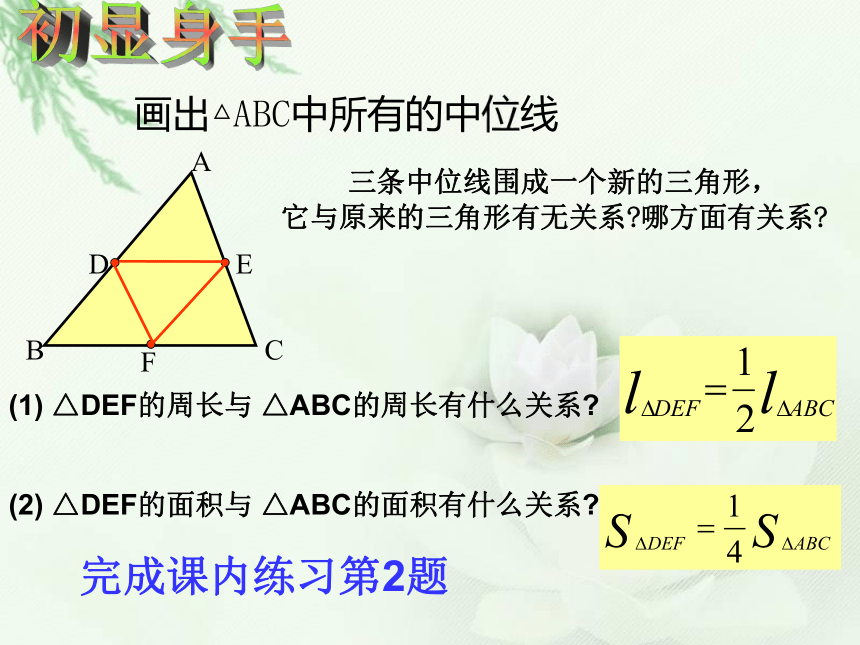
所以 DE为 △ ABC的中位线 三角形的中位线和三角形的中线有什么区别?同理DF、 EF也为 △ ABC的中位线EDFAF是 △ ABC的边BC上的中线猜想结论证明　DE与BC在位置上有什么关系？在数量上有什么关系？平行已知：如图，D、E分别是△ABC的边AB、AC的中点.延长DE到F使EF＝DE，连接FCF三角形中位线定理　　三角形的中位线平行于第三边，并且等于第三边的一半.几何语言：(三角形的中位线平行于第三边,并且等于它的一半)∵DE是△ABC的中位线（或AD=BD,AE=CE)∴DE∥BC,且DE= BC初显身手画出△ABC中所有的中位线 三条中位线围成一个新的三角形，
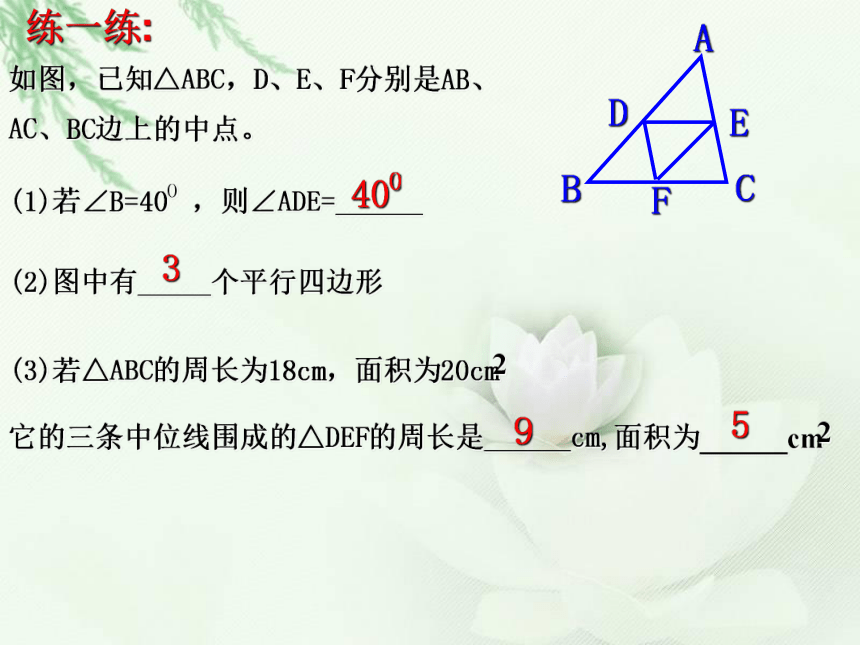
它与原来的三角形有无关系?哪方面有关系?(1) △DEF的周长与 △ABC的周长有什么关系?(2) △DEF的面积与 △ABC的面积有什么关系?完成课内练习第2题练一练:(1)若∠B=40O ，则∠ADE=______如图，已知△ABC，D、E、F分别是AB、AC、BC边上的中点。(3)若△ABC的周长为18cm，面积为20cm
它的三条中位线围成的△DEF的周长是______cm,面积为______cm
4009(2)图中有_____个平行四边形3225再显身手顺次连接任意四边形各边中点的线段
组成一个平行四边形 书上作业题3如图,DE是⊿ABC的中位线,AF是BC边上的中线,
DE和AF交于点O.求证:DE与AF互相平分.做一做
已知：如图，在四边形ABCD中，AB=CD，
M、N、P分别是AD、BC、 BD的中点。
求证：∠PNM=∠PMN想一想
已知：如图，△ABC是锐角三角形。分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN。D、E、F分别是MB、BC、CN的中点，连结DE、EF。求证：DE=EF　 布置作业:
1、作业本及分层作业本4.5 ,
2、预习4.6 校对作业题2已知: 如图,DE,EF是⊿ABC的两条中位线.
求证:四边形BFED是平行四边形.