1.3.1证明 练习题（含答案）

21世纪教育网 –中小学教育资源及组卷应用平台
证明——第一课时
班级：___________姓名：___________得分：__________
一、选择题
1、如图，下列推理中正确的是（　　）
A．若∠1=∠2，则AD∥BC
B．若∠1=∠2，则AB∥DC
C．若∠A=∠3，则AD∥BC
D．若∠3=∠4，则AB∥DC
2.如图，以下条件能判定EG∥HC的是（　　）
A．∠FEB=∠ECD B．∠AEG=∠DCH C．∠GEC=∠HCF D．∠HCF=∠AEG
3. 如图所示，CD⊥AB，垂足为D，点F是BC上任意一点，FE⊥AB，垂足为E，且∠CDG=∠BFE，∠AGD=80°，∠ACB的度数为（ ）．21世纪教育网版权所有
A.50° B.55° C.80° D.60°
4. 如图所示，两条直线AB、CD被第三条直线EF所截，∠1=75°，下列说法正确的（ ）
A．若∠4=75°，则AB∥CD
B．若∠4=105°，则AB∥CD
C．若∠2=75°，则AB∥CD
D．若∠2=155°，则AB∥CD
5. 如图： 已知∠1=40°，要使直线a∥b，则∠2=（ ）
A 50° B 40° C 140° D 150°
二、填空题
1、探照灯、锅形天线、汽车灯以及其它很多灯具都可以反射光线。如图所示是一探照灯灯碗，侧面看上去，从位于O点的灯泡发出的两束光线OB、OC经灯碗反射以后平行射出。如果图中∠ABO= a，∠DCO= ，则∠ BOC的度数为________。21教育网
2. 已知如图CD⊥AB于D，EF⊥AB于F，∠DGC=105°，∠BCG=75°，则∠1+∠2=________。
3. 如图所示，添上一个你认为适当的条件______时，a∥b．
4. 如图所示，一条公路两次转弯后，和原来的方向相同，如果第一次拐的角是36°，第二次拐的角是______度，根据______．21cnjy.com
5. 如图，给出下列三个论断：①∠B+∠D=180°；②AB∥CD；③BC∥DE．请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论栏中，使之成为一道由已知可得到结论的题目，并说明理由． www.21-cn-jy.com
已知，如图， _________ ，
结论： _________ ．
理由： _________ ．
三、解答题
1. 如图，∠1=30°，∠B=60°，AB⊥AC
（1）求∠DAB+∠B的度数．
（2）AD与BC平行吗？请说明理由．
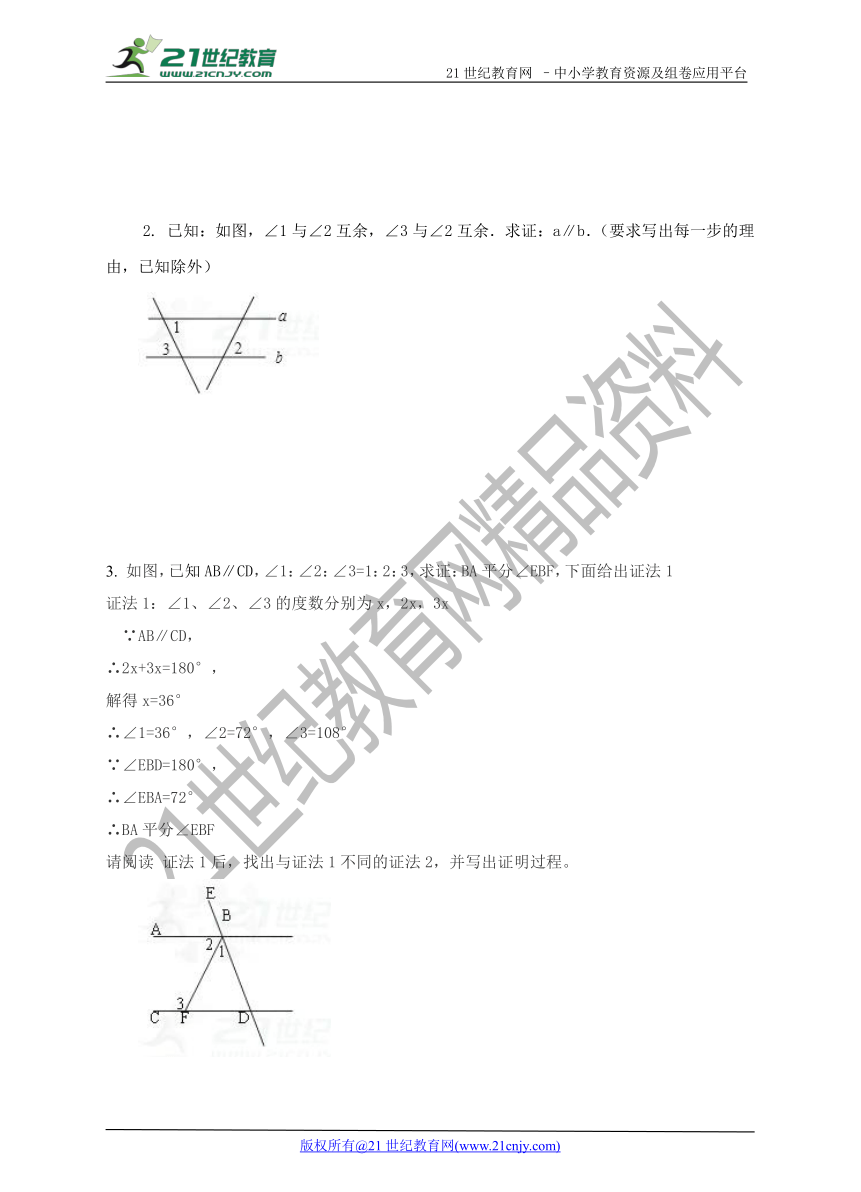
2. 已知：如图，∠1与∠2互余，∠3与∠2互余．求证：a∥b．（要求写出每一步的理由，已知除外）
3. 如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF，下面给出证法1
证法1：∠1、∠2、∠3的度数分别为x，2x，3x
∵AB∥CD，
∴2x+3x=180°，
解得x=36°
∴∠1=36°，∠2=72°，∠3=108°
∵∠EBD=180°，
∴∠EBA=72°
∴BA平分∠EBF
请阅读 证法1后，找出与证法1不同的证法2，并写出证明过程。21·cn·jy·com
四、应用题
实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．
（1）如图，一束光线m射到平面镜上，被a反射到平面镜b上，又被b镜反射，若被b反射出的光线n与光线m平行，且∠1=50°，则∠2=______°，∠3=______°；
（2）在（1）中，若∠1=55°，则∠3=______°，若∠1=40°，则∠3=______°；
（3）由（1）、（2）请你猜想：当两平面镜a、b的夹角∠3=______°时，可以使任何射到平面镜a上的光线m，经过平面镜a、b的两次反射后，入射光线m与反射光线n平行，请说明理由．2·1·c·n·j·y
参考答案
一、选择题
1、B
【解析】A、根据∠1=∠2不能推出AD∥BC，故本选项错误；
B、根据∠1=∠2能推出AB∥DC，故本选项正确；
C、根据∠A=∠3不能推出AD∥BC，故本选项错误；
D、根据∠3=∠4不能推出AB∥DC，故本选项错误．
故选B．
2、C
【解析】
A、如图，当∠FEB=∠ECD时，AB∥CD（同位角相等，两直线平行），故本选项错误；
B、如图，当∠AEG=∠DCH时，不能判定图中的哪两条直线平行，故本选项错误；
C、如图，当∠GEC=∠HCF时，EG∥HC（内错角相等，两直线平行），故本选项正确；
D、如图，当∠HCF=∠AEG时，不能判定图中的哪两条直线平行，故本选项错误；
故选：C．
3、C
【解析】证明：
∵FE⊥AB,CD⊥AB
∴CD‖EF
∴∠BCD=∠2
∵∠1=∠2
∴∠1=∠BCD
∴DG‖BC
∴∠ACB =∠3
∵∠3=80°
∴∠ACB =80°
4.B
【解析】解答：解：A、∵∠4=75°，
∴∠3=180°-75°=105°，
∴∠1≠∠3，
∴AB、CD不平行，
故此选项错误；
B、∵∠4=105°，
∴∠3=180°-105°=75°，
∴∠1=∠3，
∴AB、CD平行，
故此选项正确；
C、∵∠2=75°，
∴∠1=∠2，
又∵∠1、∠2是对顶角，
∴AB、CD不平行，
故此选项错误；
D、∵∠2=155°，
∴∠1≠∠2，
又∵∠1、∠2是对顶角，
∴∠1=∠2，
故此题矛盾，而AB、CD更不可能不平行，
故此选项错误．
故选B．
5.B
【解析】解：如图：∵直线a∥直线b，∠1=40°，
∴∠1=∠3=40°，
∴∠2=∠3=40°．
故选：B．
二、填空题
1、α+β
【解析】解：∠BOC的度数为α+β．
过O作直线EF∥AB，则EF∥CD，
∴∠1=∠ABO=α，∠2=∠DCO=β，
∴∠BOC=∠1+∠2=α+β．
2、180°
【解析】∵CD⊥AB，EF⊥AB，
∴DC∥EF，
∴∠DCB=∠BEF，
∵∠DGC=105°，∠BCG=75°，
∴∠DGC+∠BCG=180°，
∴BC∥GD，
∴∠2=∠DCB，
∴∠2=∠BEF，
∵∠1+∠BEF=180°，
∴∠1+∠2=180°．
3、∠1=∠5
【解析】答案不唯一．
∵∠1=∠5
∴a∥b（同位角相等，两直线平行）
故应填：∠1=∠5．
4. 36；两直线平行，内错角相等
【解析】根据题意得：a∥b，∠1=36°，
则可得：∠2=∠1=36°（两直线平行，内错角相等）．
故答案为：36；两直线平行，内错角相等．
5. ①②，③，平行线的判定与性质
【解析】解：如果∠B+∠D=180°，AB∥CD，那么BC∥DE．理由如下：
∵AB∥CD（已知），
∴∠B=∠C（两直线平行，内错角相等），
又∵∠B+∠D=180°（已知），
∴∠C+∠D=180°，
∴BC∥DE（同旁内角互补，两直线平行）．
故答案为：①②，③，平行线的判定与性质．
【】
三、解答题
1.【解析】
（1）∵AB⊥AC，
∴∠BAC=90°，
∵∠1=30°，∠B=60°，
∴∠DAB+∠B=180°；
（2）∵∠DAB+∠B=180°，
∴AD∥BC（同旁内角互补，两直线平行）．
2. 【解析】证明：∵∠1与∠2互余，
∴∠1+∠2=90°（余角定义），
∵∠3与∠2互余，
∴∠3+∠2=90°（余角定义），
∴∠1=∠3（等角的余角相等），
∴a∥b（内错角相等，两直线平行）．
3.【解析】解：设∠1、∠2、∠3的度数分别为x，2x，3x
则∠EBA=180°-3x，
∵AB∥CD，
∴∠2=180°-∠3=180°-3x，
∴∠EBA=∠2，
即BA平分∠EBF。
四、应用题
【解析】
（2）90°，90°．
由（1）可得∠3的度数都是90°；
（3）90°（2分）
理由：因为∠3=90°，
所以∠4+∠5=90°，
又由题意知∠1=∠4，∠5=∠6，
所以∠2+∠7=180°-（∠5+∠6）+180°-（∠1+∠4），
=360°-2∠4-2∠5，
=360°-2（∠4+∠5），
=180°．
由同旁内角互补，两直线平行，可知：m∥n．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)