1.4全等三角形 练习题（含答案）

21世纪教育网 –中小学教育资源及组卷应用平台
1.4 全等三角形
班级：___________姓名：___________得分：__________
一、选择题
1、已知下图中的两个三角形全等，则∠α度数是（ ）
A. 72° B. 60° C. 58° D. 50°
2. 已知，如图，△ABC≌△DEF，AC∥DF，BC∥EF．则不正确的等式是（　　）
A．AC=DF B．AD=BE C．DF=EF D．BC=EF
3. 在下列说法中，正确的是（　　）
A．如果两个三角形全等，则它们必是关于直线成轴对称的图形
B．如果两个三角形关于某直线成轴对称，那么它们是全等三角形
C．等腰三角形是关于底边中线成轴对称的图形
D．一条线段是关于经过该线段中点的直线成轴对称的图形
4. 如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55 °，则∠BDF等于（ ）21世纪教育网版权所有
A．55° B．60° C．70° D．90°
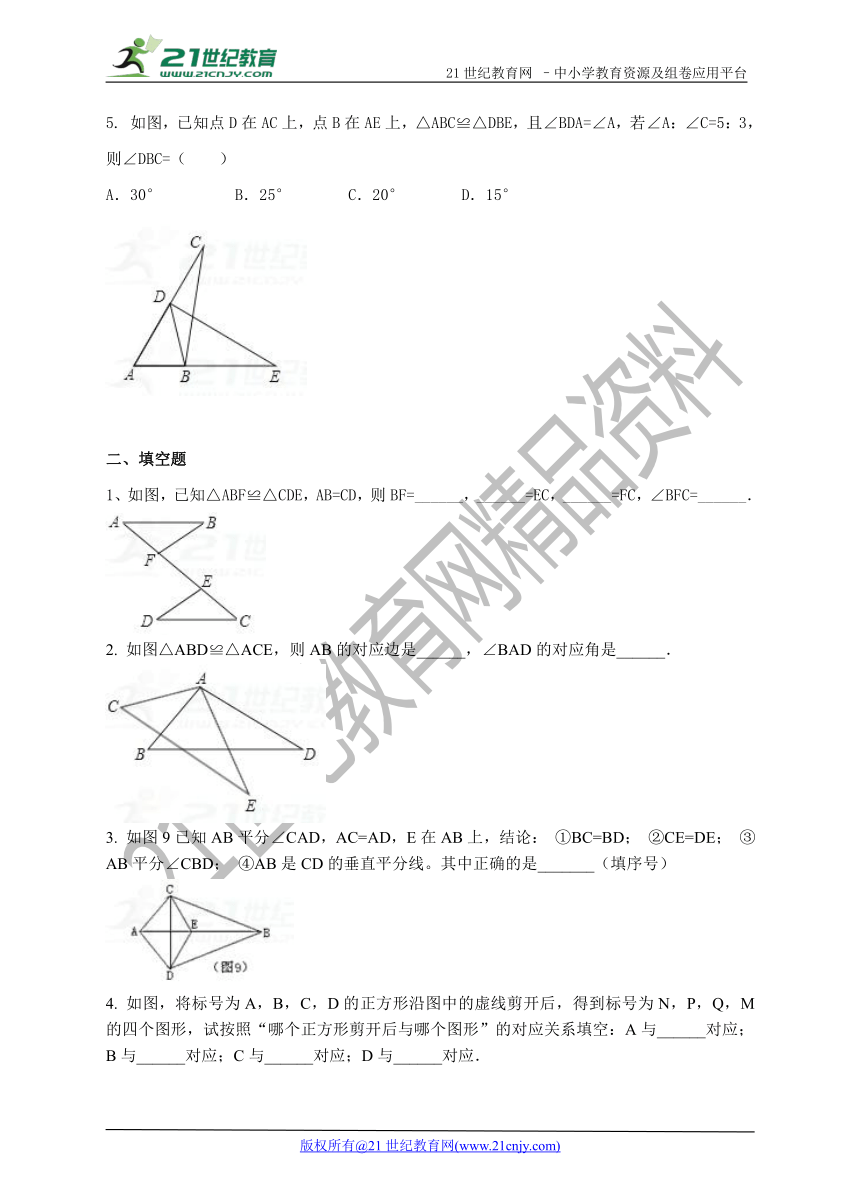
5. 如图，已知点D在AC上，点B在AE上，△ABC≌△DBE，且∠BDA=∠A，若∠A：∠C=5：3，则∠DBC=（　　）21·cn·jy·com
A．30° B．25° C．20° D．15°
二、填空题
1、如图，已知△ABF≌△CDE，AB=CD，则BF=______，______=EC，______=FC，∠BFC=______．
2. 如图△ABD≌△ACE，则AB的对应边是______，∠BAD的对应角是______．
3. 如图9已知AB平分∠CAD，AC=AD，E在AB上，结论： ①BC=BD； ②CE=DE； ③AB平分∠CBD； ④AB是CD的垂直平分线。其中正确的是_______（填序号）
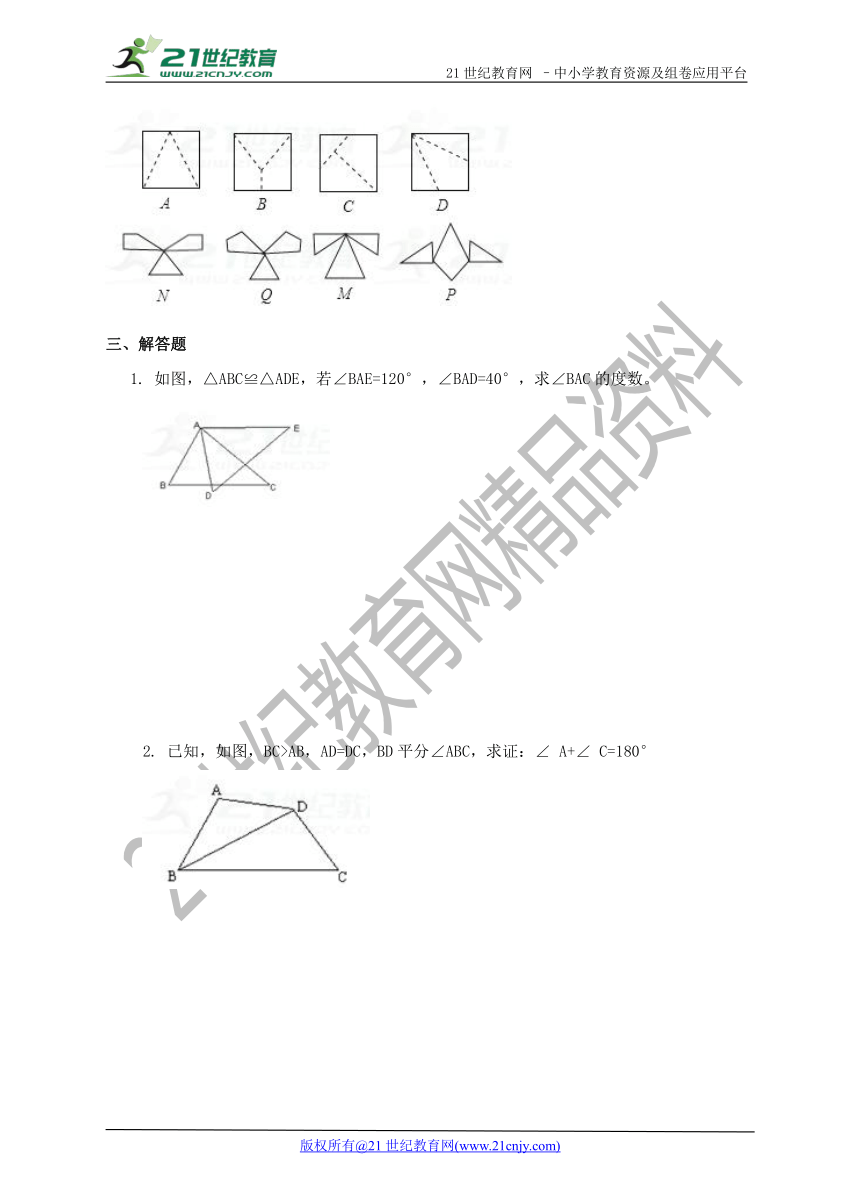
4. 如图，将标号为A，B，C，D的正方形沿图中的虚线剪开后，得到标号为N，P，Q，M的四个图形，试按照“哪个正方形剪开后与哪个图形”的对应关系填空：A与______对应；B与______对应；C与______对应；D与______对应．2·1·c·n·j·y
三、解答题
1. 如图，△ABC≌△ADE，若∠BAE=120°，∠BAD=40°，求∠BAC的度数。
2. 已知，如图，BC>AB，AD=DC，BD平分∠ABC，求证：∠ A+∠ C=180°
四、应用题
两组邻边分别相等的四边形我们称它为筝形。如图，在筝形ABCD中，AB=AD，BC=CD，AC、BD相交于点O。△ABC≌△ADCwww.21-cn-jy.com
（1）求证：AC是BD的垂直平分线；
（2）如果AC=6，BD=4，求筝形ABCD的面积
参考答案
一、选择题
1、D
【解析】由全等三角形的性质可知，α=50°
2、C
【解析】A、∵△ABC≌△DEF，∴AC=DF，故此结论正确；
B、∵△ABC≌△DEF，∴AB=DE；∵DB是公共边，∴AB-BD=DE-BD，即AD=BE；故此结论正确；
C、∵△ABC≌△DEF，∴AC=DF，故此结论DF=EF错误；
D、∵△ABC≌△DEF，∴BC=EF，故此结论正确；
故选C．
3、B
【解析】A、全等的三角形不一定是成轴对称，而成轴对称的两个三角形一定是全等的；故A错误．
B、成轴对称的两个三角形一定是全等的；故B正确．
C、等腰三角形是以底边中线所在直线为对称轴的轴对称图形或者说等腰三角形被中线所在直线分成的两个三角形成轴对称；故C错误．【来源：21·世纪·教育·网】
D、成轴对称的图形必须是两个，一个图形只能是轴对称图形；故D错误．
故选B．
4.C
【解析】∵D、E为△ABC两边AB、AC的中点，即DE是三角形的中位线．
∴DE∥BC
∴∠ADE=∠B=55°
∴∠EDF=∠ADE=55°
∴∠BDF=180-55-55=70°．
故选C．
5. C
【解析】由△ABC≌△DBE，
∴∠BDE=∠A=∠BDA，∠E=∠C，
∵∠A：∠C=5：3，
∴∠A：∠BDA：∠BDE：∠E=5：5：5：3，
又∠A+∠BDA+∠BDE+∠E=180°，
∴∠C=∠E=30°，∠BDE=∠A=∠BDA=50°，∠CDE=∠A+∠E=50°+30°=80°，
∴∠DBC=180°-∠C-∠CDE-∠BDE=180°-30°-80°-50°=20°．
故选C．
二、填空题
1、DE，AF, AE, ∠DEA
【解析】∵△ABF≌△CDE，
∴BF=DE，AF=EC，∠AFB=∠CED
∴AF+FE=EC+FE，180°-∠AFB=180°-∠CED，即：AE=FC，∠BFC=∠DEA．
2、AC；∠CAE
【解析】∵△ABD≌△ACE，
∴AB的对应边是AC，∠BAD的对应角是∠CAE；
故答案为：AC；∠CAE．
3、①②③④
【解析】先由AB平分∠CAD，AC=AD可知△ACD是等腰三角形，由等腰三角形三线合一的特点可知直线AB是线段CD的垂直平分线，再由线段垂直平分线的性质即可求解．
解：∵AC=AD，
∴△ACD是等腰三角形，
∵AB平分∠CAD，
∴AB是线段CD的垂直平分线，故④正确；
∵B、E两点在直线AB上，
∴BC=BD，CE=DE，故①②正确；
∵BC=BD，
∴△BCD是等腰三角形，
∵AB是线段CD的垂直平分线，
∴AB平分∠CBD，故③正确．
故答案为：①②③④．
4. M，N，Q，P
【】
三、解答题
1.【解析】
解：∵△ABC≌△ADE
∴∠BAC=∠DAE
∴∠DAC+∠DAB=∠DAC+∠EAC
∴∠BAD=∠EAC=40°
∵∠BAE=120°
∴∠DAC=40°
∴∠BAC=80°。
2. 【解析】
证明：作DE⊥BA，DF⊥BC
∵BD平分∠ABC
∴DE=DF
在Rt△ADE和Rt△CDF中
21教育网
四、应用题
【解析】（1）
∴∠BAO=∠DAO
，，即AC是BD的垂直平分线
（2）筝形ABCD的面积的面积+的面积

21cnjy.com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)