第1章 三角形的初步认识单元过关检测A卷
文档属性
| 名称 | 第1章 三角形的初步认识单元过关检测A卷 |  | |
| 格式 | zip | ||
| 文件大小 | 426.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-12 11:00:19 | ||
图片预览

文档简介
三角形的初步认识单元过关检测A卷
姓名:__________班级:__________学号:__________
、选择题(本大题共10小题)
1.若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
A.6 B.7 C.11 D.12
2.如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=3,则CF的长为( ) www.21-cn-jy.com
A.4 B.4.5 C.6 D.92·1·c·n·j·y
3.下列四个图形中,线段BE是△ABC的高的是( )
A. B. C. D.
4.下列图形中有稳定性的是( )
A. 正方形 B. 直角三角形 C. 长方形 D. 平行四边形www-2-1-cnjy-com
5.如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( )
A.145° B.150° C.155° D.160°
6.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )【来源:21cnj*y.co*m】
A.15° B.20° C.25° D.30°
8.如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
9.如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )
A. 30° B. 40° C. 50° D. 60°
10.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )【版权所有:21教育】
A.SSS B.SAS C.ASA D.AAS
、填空题(本大题共8小题)
11.如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA= .
12.造房子时,屋顶常用三角形结构,从数学角度来看,是应用了__________,而活动挂架则用了四边形的__________.21*cnjy*com
13.如图,a∥b ,∠1+∠2=75°,则∠3+∠4= ____________.
14.如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
15.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B= .
16.如图,BC∥EF,AC∥DF,添加一个条件 ,使得△ABC≌△DEF.
17.如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于__________度.
18.如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 .
、解答题(本大题共9小题)
如图,在△ABC中AD⊥BC,AE平分∠BAC交BC于E,∠B=300, ∠C=700 ,求∠EAD的度数。
,
20.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.21·世纪*教育网
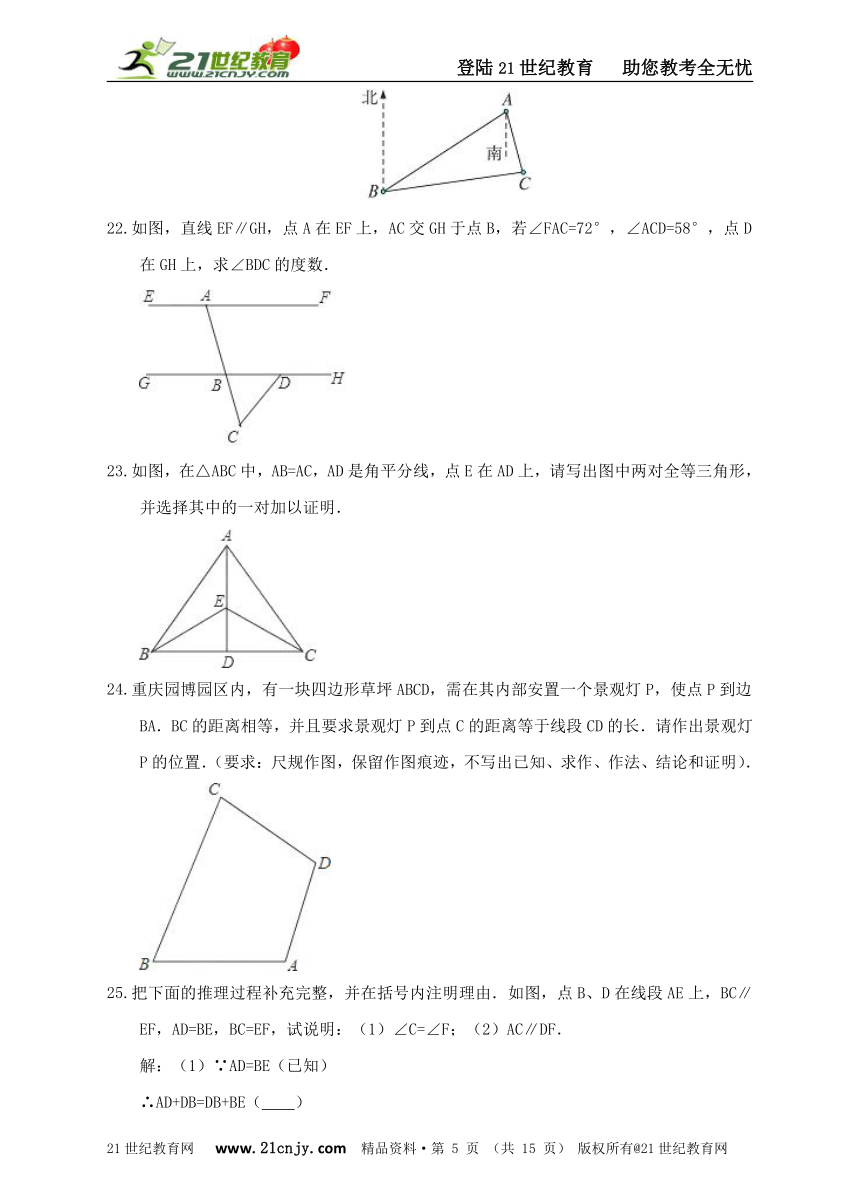
21.如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.2-1-c-n-j-y
22.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
23.如图,在△ABC中,AB=AC,AD是角平分线,点E在AD上,请写出图中两对全等三角形,并选择其中的一对加以证明.
24.重庆园博园区内,有一块四边形草坪ABCD,需在其内部安置一个景观灯P,使点P到边BA.BC的距离相等,并且要求景观灯P到点C的距离等于线段CD的长.请作出景观灯P的位置.(要求:尺规作图,保留作图痕迹,不写出已知、求作、作法、结论和证明).
25.把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠ ( )
又∵BC=EF(已知)
∴△ABC≌△DEF( )
∴∠C=∠F,∠A=∠FDE( )
∴AC∥DF( )
26.如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.
求证:BE=CF.
27.如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)求证:△ACD≌△BCE;
(2)若∠D=47°,求∠B的度数.
答案解析
、选择题
1.【分析】首先求出三角形第三边的取值范围,进而求出三角形的周长取值范围,据此求出答案.
解:设第三边的长为x,
∵三角形两边的长分别是2和4,
∴4﹣2<x<2+4,即2<x<6.
则三角形的周长:8<C<12,
C选项11符合题意,
故选C.
2.【分析】根据三角形重心的性质,求出FG=CG,然后即可求出CF的长解:∵点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,21cnjy.com
∴G为△ABC的重心,∴2FG=GC,
∵FG=3,∴GC=6,∴CF=9.
故选D..
3.【分析】根据三角形的高的定义,过顶点向对边作垂线,顶点与垂足之间的线段为三角形的高,观察各选项直接选择答案即可.21·cn·jy·com
解:线段BE是△ABC的高的图是选项D.
故选D.
4.解:B
5.【分析】根据三角形内角和定理求出x,再根据三角形的外角的等于不相邻的两个内角的和,即可解决问题.
解:在△ABC中,∵∠B+∠C+∠BAC=180°,∠BAC=x°,∠B=2x°,∠C=3x°,
∴6x=180,
∴x=30,
∵∠BAD=∠B+∠C=5x=150°,
故选B.
6.【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.
解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选A.
7.【分析】根据全等三角形对应角相等,∠A=∠BED=∠CED,∠ABD=∠EBD=∠C,根据∠BED+∠CED=180°,可以得到∠A=∠BED=∠CED=90°,再利用三角形的内角和定理求解即可.
解:∵△ADB≌△EDB≌△EDC
∴∠A=∠BED=∠CED,∠ABD=∠EBD=∠C
∵∠BED+∠CED=180°
∴∠A=∠BED=∠CED=90°
在△ABC中,∠C+2∠C+90°=180°
∴∠C=30°
故选D.
8.【分析】本题可以假设A.B、C、D选项成立,分别证明△ABC≌△DEF,即可解题.
解:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故D选项错误;【出处:21教育名师】
故选:C.
9.【分析】 根据直角三角形两锐角互余求出∠3,再利用“HL”证明Rt△ABC和Rt△ADC全等,根据全等三角形对应角相等可得∠2=∠3.
解答: 解:∵∠B=90°,∠1=30°,
∴∠3=90°﹣∠1=90°﹣30°=60°,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠2=∠3=60°.
故选D.
10.【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:C.
、填空题
11.【分析】根据三角形的重心到顶点的长度等于到对边中点的长度的2倍可得OD=AO,再根据等高的三角形的面积等于底边的比求出△AOB的面积.21教育名师原创作品
解:∵中线AD、BE相交于点O,
∴O是△ABC的重心,
∴OD=AO,
∵S△BOD=5,
∴S△AOB=2S△BOD=2×5=10.
故答案为:10.
12.解:三角形的稳定性 不稳定性
13.【分析】根据平行线的性质;三角形内角和定理求解
解:∵∠5=∠1+∠2=75°, a∥b,
∴∠3=∠6 ,
∴∠3+∠4=∠6+∠4=180°-75° =105°
14.【分析】先延长AP交直线b于C,再根据平行线的性质以及三角形的外角性质进行计算即可.
解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
15.【分析】根据全等三角形的性质求出∠C的度数,根据三角形内角和定理计算即可.
解:∵△ABC≌△A′B′C′,
∴∠C=∠C′=24°,
∴∠B=180°﹣∠A﹣∠B=120°,
故答案为:120°.
16.【分析】本题要判定△ABC≌△DEF,易证∠A=∠EDF,∠ABC=∠E,故添加AB=DE、BC=EF或AC=DF根据ASA.AAS即可解题.21世纪教育网版权所有
解:∵BC∥EF,
∴∠ABC=∠E,
∵AC∥DF,
∴∠A=∠EDF,
∵在△ABC和△DEF中,,
∴△ABC≌△DEF,
同理,BC=EF或AC=DF也可证△ABC≌△DEF.
故答案为AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可).
17.【分析】根据SSS证△BAD≌△CAD,根据全等得出∠BAD=∠CAD,∠B=∠C=20°,根据三角形的外角性质得出∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,求出∠BDC=∠B+∠C+∠BAC,代入求出即可.21教育网
【解答】解:过D作射线AF,
在△BAD和△CAD中,
,
∴△BAD≌△CAD(SSS),
∴∠BAD=∠CAD,∠B=∠C=20°,
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
∴∠BDC=∠B+∠C+∠BAC,
∵∠C=∠B=20°,∠BDC=120°,
∴∠BAC=80°.
故答案为:80.
18.【分析】直接根据角平分线的作法即可得出结论.
解:∵由作法可知,OC是∠AOB的平分线,
∴∠AOC=∠AOB=20°.
故答案为:20°.
、解答题
19.解:∵∠B=30°,∠C=70°
∴∠BAC=180°-(∠B+∠C)=80°
∵
∴∠BAE=∠BAC =40°
∴∠AED=∠BAE+∠B=70°
∵
∴∠EAD=90°-∠AED=20°
20.【分析】先根据三角形内角和定理,求得∠B+∠C=110°,再根据∠B=∠DEB,∠C=∠DFC,求得∠B+∠DEB+∠C+∠DFC=220°,最后根据三角形内角和,求得∠EDF即可.
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=110°,
∵∠B=∠DEB,∠C=∠DFC,
∴∠B+∠DEB+∠C+∠DFC=220°,
∵∠B+∠DEB+∠C+∠DFC+∠EDB+∠FDC=360°,
∴∠EDB+∠FDC=140°,
即∠EDF=180°﹣140°=40°
21.解:∵BD∥AE,
∴∠DBA=∠BAE=57°.
∴∠ABC=∠DBC-∠DBA=82°-57°=25°.
在△ABC中,∠BAC=∠BAE+∠CAE=57°+15°=72°,
∴∠C=180°-∠ABC-∠BAC=180°-25°-72°=83°.
22.【分析】由平行线的性质求出∠ABD=108°,由三角形的外角性质得出∠ABD=∠ACD+∠BDC,即可求出∠BDC的度数.【来源:21·世纪·教育·网】
解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
23.【分析】由AB=AC,AD是角平分线,即可利用(SAS)证出△ABD≌△ACD,同理可得出△ABE≌△ACE,△EBD≌△ECD.21*cnjy*com
解:△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.
以△ABE≌△ACE为例,证明如下:
∵AD平分∠BAC,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS).
24.【分析】首先画出∠ABC的角平分线,再以C为圆心,CD长为半径画弧,交BD于点P,P即为所求.
解:如图所示:
,
P点即为所求.
25.【分析】(1)由等式的性质、平行线的性质以及全等三角形的判定和性质即可得出结果;
(2)由同位角相等,即可得出结论.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( 等式的性质)
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠E( 两直线平行,同位角相等)
又∵BC=EF(已知)
∴△ABC≌△DEF( SAS)
∴∠C=∠F,∠A=∠FDE( 全等三角形的对应角相等);
故答案为:等式的性质;E; 两直线平行,同位角相等;SAS;全等三角形的对应角相等;
(2)∵∠A=∠FDE,
∴AC∥DF( 同位角相等,两直线平行 ).
故答案为:同位角相等,两直线平行.
26.【分析】 易证△BED≌△CFD,根据全等三角形对应边相等的性质即可解题.
解答: 解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF.
27.【分析】 (1)要使△ACD≌△BCE,已知C是线段AB的中点,所以有AC=BC,又因为CD平分∠ACE,CE平分∠BCD,所以∠ACD=∠BCE,故可根据SAS判定两三角形全等.
(2)由△ACD≌△BCE,得到∠D=∠E,根据平角的定义得到∠1+∠2+∠3=180°由∠1=∠2=∠3,得到∠1=∠2=∠3=60°,求得∠B=180°﹣∠3﹣∠E=73°.
解答: 解:(1)证明:∵C是线段AB的中点
∴AC=BC
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠D=∠E=47°,
∵∠1+∠2+∠3=180°,∠1=∠2=∠3,
∴∠1=∠2=∠3=60°,
∴∠B=180°﹣∠3﹣∠E=73°.
姓名:__________班级:__________学号:__________
、选择题(本大题共10小题)
1.若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
A.6 B.7 C.11 D.12
2.如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=3,则CF的长为( ) www.21-cn-jy.com
A.4 B.4.5 C.6 D.92·1·c·n·j·y
3.下列四个图形中,线段BE是△ABC的高的是( )
A. B. C. D.
4.下列图形中有稳定性的是( )
A. 正方形 B. 直角三角形 C. 长方形 D. 平行四边形www-2-1-cnjy-com
5.如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( )
A.145° B.150° C.155° D.160°
6.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )【来源:21cnj*y.co*m】
A.15° B.20° C.25° D.30°
8.如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
9.如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )
A. 30° B. 40° C. 50° D. 60°
10.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )【版权所有:21教育】
A.SSS B.SAS C.ASA D.AAS
、填空题(本大题共8小题)
11.如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA= .
12.造房子时,屋顶常用三角形结构,从数学角度来看,是应用了__________,而活动挂架则用了四边形的__________.21*cnjy*com
13.如图,a∥b ,∠1+∠2=75°,则∠3+∠4= ____________.
14.如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
15.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B= .
16.如图,BC∥EF,AC∥DF,添加一个条件 ,使得△ABC≌△DEF.
17.如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于__________度.
18.如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 .
、解答题(本大题共9小题)
如图,在△ABC中AD⊥BC,AE平分∠BAC交BC于E,∠B=300, ∠C=700 ,求∠EAD的度数。
,
20.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.21·世纪*教育网
21.如图,经测量,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向,求∠C的度数.2-1-c-n-j-y
22.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
23.如图,在△ABC中,AB=AC,AD是角平分线,点E在AD上,请写出图中两对全等三角形,并选择其中的一对加以证明.
24.重庆园博园区内,有一块四边形草坪ABCD,需在其内部安置一个景观灯P,使点P到边BA.BC的距离相等,并且要求景观灯P到点C的距离等于线段CD的长.请作出景观灯P的位置.(要求:尺规作图,保留作图痕迹,不写出已知、求作、作法、结论和证明).
25.把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠ ( )
又∵BC=EF(已知)
∴△ABC≌△DEF( )
∴∠C=∠F,∠A=∠FDE( )
∴AC∥DF( )
26.如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.
求证:BE=CF.
27.如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)求证:△ACD≌△BCE;
(2)若∠D=47°,求∠B的度数.
答案解析
、选择题
1.【分析】首先求出三角形第三边的取值范围,进而求出三角形的周长取值范围,据此求出答案.
解:设第三边的长为x,
∵三角形两边的长分别是2和4,
∴4﹣2<x<2+4,即2<x<6.
则三角形的周长:8<C<12,
C选项11符合题意,
故选C.
2.【分析】根据三角形重心的性质,求出FG=CG,然后即可求出CF的长解:∵点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,21cnjy.com
∴G为△ABC的重心,∴2FG=GC,
∵FG=3,∴GC=6,∴CF=9.
故选D..
3.【分析】根据三角形的高的定义,过顶点向对边作垂线,顶点与垂足之间的线段为三角形的高,观察各选项直接选择答案即可.21·cn·jy·com
解:线段BE是△ABC的高的图是选项D.
故选D.
4.解:B
5.【分析】根据三角形内角和定理求出x,再根据三角形的外角的等于不相邻的两个内角的和,即可解决问题.
解:在△ABC中,∵∠B+∠C+∠BAC=180°,∠BAC=x°,∠B=2x°,∠C=3x°,
∴6x=180,
∴x=30,
∵∠BAD=∠B+∠C=5x=150°,
故选B.
6.【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.
解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选A.
7.【分析】根据全等三角形对应角相等,∠A=∠BED=∠CED,∠ABD=∠EBD=∠C,根据∠BED+∠CED=180°,可以得到∠A=∠BED=∠CED=90°,再利用三角形的内角和定理求解即可.
解:∵△ADB≌△EDB≌△EDC
∴∠A=∠BED=∠CED,∠ABD=∠EBD=∠C
∵∠BED+∠CED=180°
∴∠A=∠BED=∠CED=90°
在△ABC中,∠C+2∠C+90°=180°
∴∠C=30°
故选D.
8.【分析】本题可以假设A.B、C、D选项成立,分别证明△ABC≌△DEF,即可解题.
解:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故D选项错误;【出处:21教育名师】
故选:C.
9.【分析】 根据直角三角形两锐角互余求出∠3,再利用“HL”证明Rt△ABC和Rt△ADC全等,根据全等三角形对应角相等可得∠2=∠3.
解答: 解:∵∠B=90°,∠1=30°,
∴∠3=90°﹣∠1=90°﹣30°=60°,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠2=∠3=60°.
故选D.
10.【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:C.
、填空题
11.【分析】根据三角形的重心到顶点的长度等于到对边中点的长度的2倍可得OD=AO,再根据等高的三角形的面积等于底边的比求出△AOB的面积.21教育名师原创作品
解:∵中线AD、BE相交于点O,
∴O是△ABC的重心,
∴OD=AO,
∵S△BOD=5,
∴S△AOB=2S△BOD=2×5=10.
故答案为:10.
12.解:三角形的稳定性 不稳定性
13.【分析】根据平行线的性质;三角形内角和定理求解
解:∵∠5=∠1+∠2=75°, a∥b,
∴∠3=∠6 ,
∴∠3+∠4=∠6+∠4=180°-75° =105°
14.【分析】先延长AP交直线b于C,再根据平行线的性质以及三角形的外角性质进行计算即可.
解:如图所示,延长AP交直线b于C,
∵a∥b,
∴∠C=∠1=35°,
∵∠APB是△BCP的外角,PA⊥PB,
∴∠2=∠APB﹣∠C=90°﹣35°=55°,
故答案为:55°.
15.【分析】根据全等三角形的性质求出∠C的度数,根据三角形内角和定理计算即可.
解:∵△ABC≌△A′B′C′,
∴∠C=∠C′=24°,
∴∠B=180°﹣∠A﹣∠B=120°,
故答案为:120°.
16.【分析】本题要判定△ABC≌△DEF,易证∠A=∠EDF,∠ABC=∠E,故添加AB=DE、BC=EF或AC=DF根据ASA.AAS即可解题.21世纪教育网版权所有
解:∵BC∥EF,
∴∠ABC=∠E,
∵AC∥DF,
∴∠A=∠EDF,
∵在△ABC和△DEF中,,
∴△ABC≌△DEF,
同理,BC=EF或AC=DF也可证△ABC≌△DEF.
故答案为AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可).
17.【分析】根据SSS证△BAD≌△CAD,根据全等得出∠BAD=∠CAD,∠B=∠C=20°,根据三角形的外角性质得出∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,求出∠BDC=∠B+∠C+∠BAC,代入求出即可.21教育网
【解答】解:过D作射线AF,
在△BAD和△CAD中,
,
∴△BAD≌△CAD(SSS),
∴∠BAD=∠CAD,∠B=∠C=20°,
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
∴∠BDC=∠B+∠C+∠BAC,
∵∠C=∠B=20°,∠BDC=120°,
∴∠BAC=80°.
故答案为:80.
18.【分析】直接根据角平分线的作法即可得出结论.
解:∵由作法可知,OC是∠AOB的平分线,
∴∠AOC=∠AOB=20°.
故答案为:20°.
、解答题
19.解:∵∠B=30°,∠C=70°
∴∠BAC=180°-(∠B+∠C)=80°
∵
∴∠BAE=∠BAC =40°
∴∠AED=∠BAE+∠B=70°
∵
∴∠EAD=90°-∠AED=20°
20.【分析】先根据三角形内角和定理,求得∠B+∠C=110°,再根据∠B=∠DEB,∠C=∠DFC,求得∠B+∠DEB+∠C+∠DFC=220°,最后根据三角形内角和,求得∠EDF即可.
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=110°,
∵∠B=∠DEB,∠C=∠DFC,
∴∠B+∠DEB+∠C+∠DFC=220°,
∵∠B+∠DEB+∠C+∠DFC+∠EDB+∠FDC=360°,
∴∠EDB+∠FDC=140°,
即∠EDF=180°﹣140°=40°
21.解:∵BD∥AE,
∴∠DBA=∠BAE=57°.
∴∠ABC=∠DBC-∠DBA=82°-57°=25°.
在△ABC中,∠BAC=∠BAE+∠CAE=57°+15°=72°,
∴∠C=180°-∠ABC-∠BAC=180°-25°-72°=83°.
22.【分析】由平行线的性质求出∠ABD=108°,由三角形的外角性质得出∠ABD=∠ACD+∠BDC,即可求出∠BDC的度数.【来源:21·世纪·教育·网】
解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
23.【分析】由AB=AC,AD是角平分线,即可利用(SAS)证出△ABD≌△ACD,同理可得出△ABE≌△ACE,△EBD≌△ECD.21*cnjy*com
解:△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.
以△ABE≌△ACE为例,证明如下:
∵AD平分∠BAC,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS).
24.【分析】首先画出∠ABC的角平分线,再以C为圆心,CD长为半径画弧,交BD于点P,P即为所求.
解:如图所示:
,
P点即为所求.
25.【分析】(1)由等式的性质、平行线的性质以及全等三角形的判定和性质即可得出结果;
(2)由同位角相等,即可得出结论.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( 等式的性质)
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠E( 两直线平行,同位角相等)
又∵BC=EF(已知)
∴△ABC≌△DEF( SAS)
∴∠C=∠F,∠A=∠FDE( 全等三角形的对应角相等);
故答案为:等式的性质;E; 两直线平行,同位角相等;SAS;全等三角形的对应角相等;
(2)∵∠A=∠FDE,
∴AC∥DF( 同位角相等,两直线平行 ).
故答案为:同位角相等,两直线平行.
26.【分析】 易证△BED≌△CFD,根据全等三角形对应边相等的性质即可解题.
解答: 解:∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF.
27.【分析】 (1)要使△ACD≌△BCE,已知C是线段AB的中点,所以有AC=BC,又因为CD平分∠ACE,CE平分∠BCD,所以∠ACD=∠BCE,故可根据SAS判定两三角形全等.
(2)由△ACD≌△BCE,得到∠D=∠E,根据平角的定义得到∠1+∠2+∠3=180°由∠1=∠2=∠3,得到∠1=∠2=∠3=60°,求得∠B=180°﹣∠3﹣∠E=73°.
解答: 解:(1)证明:∵C是线段AB的中点
∴AC=BC
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠D=∠E=47°,
∵∠1+∠2+∠3=180°,∠1=∠2=∠3,
∴∠1=∠2=∠3=60°,
∴∠B=180°﹣∠3﹣∠E=73°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
