1.5三角形全等的判定(3) 练习题(含答案)
文档属性
| 名称 | 1.5三角形全等的判定(3) 练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-12 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
三角形全等的判定(3)
班级:___________姓名:___________得分:__________
一、选择题
1、如图,△ABC中,点D在BC上,点E在AB上,BD=BE,下列四个条件中,不能使△ADB≌△CEB的条件是( )21教育网
A.AD=CE B.AE=CD C.∠BAC=∠BCA D.∠ADB=∠CEB
2. 小明不慎将三角形模具打碎为四块,若他只带其中一块到商店去,就能还配一块与原来一模一样的三角形模具,应带( )块去合适.21cnjy.com
A.A B.B C.C D.D
3. 如图所示,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还须补充的一个条件是( )
A.AB=DE B.∠ACE=∠DFB C.BF=EC D.∠ABC=∠DEF
4. 下面说法正确的是( )
A.有两边和一角对应相等的两个三角形全等
B.有两角和它们的夹边对应相等的两个三角形全等
C.两个等边三角形一定全等
D.两个等腰直角三角形一定全等
5. 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A. 边角边 B. 角边角 C. 边边边 D. 边边角
二、填空题
1、如图,若∠DAB=∠CBA,∠DBA=∠CAB,使△ABD≌△BAC,三角形全等的理由是______.
2. 如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是______.2·1·c·n·j·y
3. 填“一定”或“不一定”:
(1)两边对应相等的两个三角形______全等;
(2)一边一角对应相等的两个三角形______全等;
(3)两角对应相等的两个三角形______全等;
(4)三边对应相等的两个三角形______全等;
(5)两边和它们的夹角对应相等的两个三角形______全等;
(6)两边和其中一边的对角对应相等的两个三角形______全等;
(7)两角和它们的夹边对应相等的两个三角形______全等;
4. 初一(1)班的篮球拉拉队,为了在明天的比赛中给同学加油助威,每个人都提前制作了一面同一规格的三角形彩旗.小明放学回家后,发现自己的彩旗破损了一角,他想用彩纸重新制作一面彩旗(如图所示).于是小明挑选了其中的一块,准备用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形,你认为他作图的根据是______.(只要填写两个三角形全等的一个条件)【来源:21·世纪·教育·网】
三、证明题
1. 已知:如图,在正方形ABCD中,AE⊥BF,垂足为P,AE与CD交于点E,BF与AD交于点F,求证:AE=BF。21·世纪*教育网
2. 如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF。
四、探究题
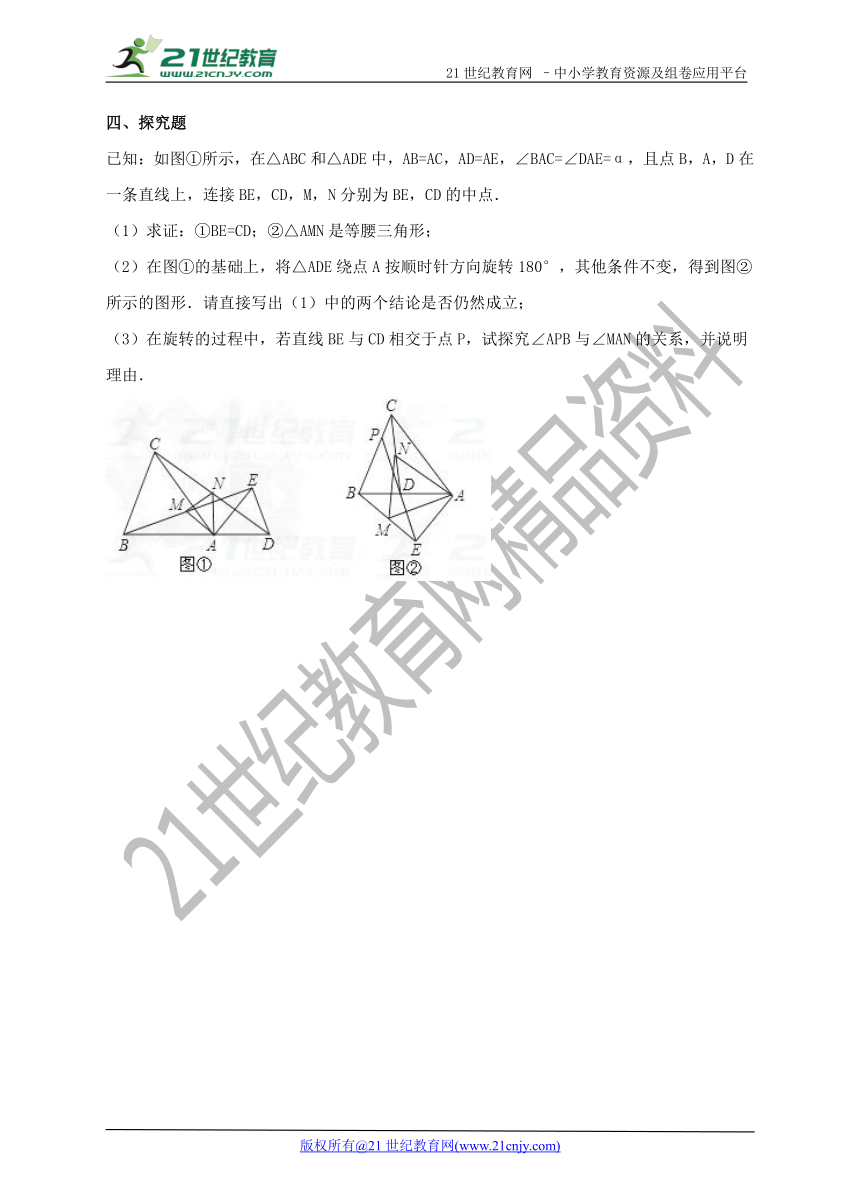
已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.21世纪教育网版权所有
(1)求证:①BE=CD;②△AMN是等腰三角形;
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;www.21-cn-jy.com
(3)在旋转的过程中,若直线BE与CD相交于点P,试探究∠APB与∠MAN的关系,并说明理由.
参考答案
一、选择题
1、A
【解析】已知△ADB和△CEB隐含条件∠B=∠B,
A、根据AD=CE,BD=BE和∠B=∠B不能推出两三角形全等,错误,故本选项正确;
B、∵AE=CD,BE=BD,
∴AB=BC,
∵在△ADB和△CEB中
AB=BC ∠B=∠B BD=BE ,
∴△ADB≌△CEB(SAS),正确,故本选项错误;
C、∵∠BAC=∠BCA,
∴AB=BC,
∵在△ADB和△CEB中
AB=BC ∠B=∠B BD=BE ,
∴△ADB≌△CEB(SAS),正确,故本选项错误;
D、∵在△ADB和△CEB中
∠B=∠B BD=BE ∠ADB=∠CEB ,
∴△ADB≌△CEB(ASA),正确,故本选项错误;
故选A.
2、D
【解析】A只保留了一个角及部分边,不能配成和原来一样的三角形玻璃;
B,C则只保留了部分边,不能配成和原来一样的三角形玻璃;
而D不但保留了一个完整的边还保留了两个角,所以应该带“D”去,根据全等三角形判定“ASA”可以配出一块和原来一样的三角形玻璃.21·cn·jy·com
故选D.
3、D
【解析】A、添加条件AB=DE,满足SSA无法判定两个三角形全等;
B、添加条件∠ACE=∠DFB,无法判定两个三角形全等;
C、添加条件BF=EC,无法判定两个三角形全等;
D、添加条件∠ABC=∠DEF后,符合ASA,能证明三角形全等.
故选D.
4.B
【解析】A、因为该角不一定是夹角,故错误;
B、符合全等三角形的判定方法ASA,故正确;
C、两个等边三角形的边不一定相等,故错误;
D、两个等腰直角三角形的边不一定相等,故错误.
故选B
5.B
【解析】∵BF⊥AB,DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA)
故选B.
二、填空题
1、ASA(或者角边角)
【解析】∵∠DAB=∠CBA,
AB为公共边
∠DBA=∠CAB
∴则△ABD≌△BAC (ASA)
2、∠A=∠B
【解析】添加的条件为∠A=∠B,理由为:
∵EC⊥AB,DF⊥AB,
∴∠ADF=∠BCE=90°,
在△AFD和△BEC中,
∠A=∠B AD=BC ∠ADF=∠BCE ,
∴△AFD≌△BEC(ASA).
3、不一定 不一定 不一定 一定 一定 不一定 一定
【解析】(1)两边对应相等的两个三角形不一定全等;
(2)一边一角对应相等的两个三角形不一定全等;
(3)两角对应相等的两个三角形不一定全等;
(4)三边对应相等的两个三角形一定全等(根据SSS可判定全等);
(5)两边和它们的夹角对应相等的两个三角形一定全等(根据SAS可判定全等);
(6)两边和其中一边的对角对应相等的两个三角形不一定全等;
(7)两角和它们的夹边对应相等的两个三角形一定全等(根据ASA可判定全等);
4. ASA
【解析】
如图所示:
根据已知两角和它们的夹边相等得出全等三角形,
故答案为:ASA.
三、解答题
1.【解析】
证明 :∵AE⊥BF ∠BAP=∠AED
∴∠ABF=∠DAE
∵AB=AD ∠FAB=∠EDA
∴△ABF≌△ADE
∴AE=BF
2. 【解析】
证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BC=EF,
∵∠ACB=∠F,
∵∠B=∠DEF,BC=EF,∠ACB=∠F
∴△ABC≌△DEF。(ASA)
四、探究题
②∵△ABE≌△ACD,
∴∠ABE=∠ACD,
BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,
即△AMN为等腰三角形.
(2)解:(1)中的两个结论仍然成立.
(3)证明:在图②中正确画出线段PD,
由(1)同理可证△ABM≌△ACN,
∴∠CAN=∠BAM,
∴∠BAC=∠MAN.
又∵∠BAC=∠DAE,
∴∠MAN=∠DAE=∠BAC.
∴△AMN,△ADE和△ABC都是顶角相等的等腰三角形.
∴△PBD和△AMN都为顶角相等的等腰三角形,
∴∠PBD=∠AMN,∠PDB=∠ANM,
∴△PBD∽△AMN.
∴∠APB=∠MAN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
三角形全等的判定(3)
班级:___________姓名:___________得分:__________
一、选择题
1、如图,△ABC中,点D在BC上,点E在AB上,BD=BE,下列四个条件中,不能使△ADB≌△CEB的条件是( )21教育网
A.AD=CE B.AE=CD C.∠BAC=∠BCA D.∠ADB=∠CEB
2. 小明不慎将三角形模具打碎为四块,若他只带其中一块到商店去,就能还配一块与原来一模一样的三角形模具,应带( )块去合适.21cnjy.com
A.A B.B C.C D.D
3. 如图所示,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还须补充的一个条件是( )
A.AB=DE B.∠ACE=∠DFB C.BF=EC D.∠ABC=∠DEF
4. 下面说法正确的是( )
A.有两边和一角对应相等的两个三角形全等
B.有两角和它们的夹边对应相等的两个三角形全等
C.两个等边三角形一定全等
D.两个等腰直角三角形一定全等
5. 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A. 边角边 B. 角边角 C. 边边边 D. 边边角
二、填空题
1、如图,若∠DAB=∠CBA,∠DBA=∠CAB,使△ABD≌△BAC,三角形全等的理由是______.
2. 如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是______.2·1·c·n·j·y
3. 填“一定”或“不一定”:
(1)两边对应相等的两个三角形______全等;
(2)一边一角对应相等的两个三角形______全等;
(3)两角对应相等的两个三角形______全等;
(4)三边对应相等的两个三角形______全等;
(5)两边和它们的夹角对应相等的两个三角形______全等;
(6)两边和其中一边的对角对应相等的两个三角形______全等;
(7)两角和它们的夹边对应相等的两个三角形______全等;
4. 初一(1)班的篮球拉拉队,为了在明天的比赛中给同学加油助威,每个人都提前制作了一面同一规格的三角形彩旗.小明放学回家后,发现自己的彩旗破损了一角,他想用彩纸重新制作一面彩旗(如图所示).于是小明挑选了其中的一块,准备用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形,你认为他作图的根据是______.(只要填写两个三角形全等的一个条件)【来源:21·世纪·教育·网】
三、证明题
1. 已知:如图,在正方形ABCD中,AE⊥BF,垂足为P,AE与CD交于点E,BF与AD交于点F,求证:AE=BF。21·世纪*教育网
2. 如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF。
四、探究题
已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.21世纪教育网版权所有
(1)求证:①BE=CD;②△AMN是等腰三角形;
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;www.21-cn-jy.com
(3)在旋转的过程中,若直线BE与CD相交于点P,试探究∠APB与∠MAN的关系,并说明理由.
参考答案
一、选择题
1、A
【解析】已知△ADB和△CEB隐含条件∠B=∠B,
A、根据AD=CE,BD=BE和∠B=∠B不能推出两三角形全等,错误,故本选项正确;
B、∵AE=CD,BE=BD,
∴AB=BC,
∵在△ADB和△CEB中
AB=BC ∠B=∠B BD=BE ,
∴△ADB≌△CEB(SAS),正确,故本选项错误;
C、∵∠BAC=∠BCA,
∴AB=BC,
∵在△ADB和△CEB中
AB=BC ∠B=∠B BD=BE ,
∴△ADB≌△CEB(SAS),正确,故本选项错误;
D、∵在△ADB和△CEB中
∠B=∠B BD=BE ∠ADB=∠CEB ,
∴△ADB≌△CEB(ASA),正确,故本选项错误;
故选A.
2、D
【解析】A只保留了一个角及部分边,不能配成和原来一样的三角形玻璃;
B,C则只保留了部分边,不能配成和原来一样的三角形玻璃;
而D不但保留了一个完整的边还保留了两个角,所以应该带“D”去,根据全等三角形判定“ASA”可以配出一块和原来一样的三角形玻璃.21·cn·jy·com
故选D.
3、D
【解析】A、添加条件AB=DE,满足SSA无法判定两个三角形全等;
B、添加条件∠ACE=∠DFB,无法判定两个三角形全等;
C、添加条件BF=EC,无法判定两个三角形全等;
D、添加条件∠ABC=∠DEF后,符合ASA,能证明三角形全等.
故选D.
4.B
【解析】A、因为该角不一定是夹角,故错误;
B、符合全等三角形的判定方法ASA,故正确;
C、两个等边三角形的边不一定相等,故错误;
D、两个等腰直角三角形的边不一定相等,故错误.
故选B
5.B
【解析】∵BF⊥AB,DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA)
故选B.
二、填空题
1、ASA(或者角边角)
【解析】∵∠DAB=∠CBA,
AB为公共边
∠DBA=∠CAB
∴则△ABD≌△BAC (ASA)
2、∠A=∠B
【解析】添加的条件为∠A=∠B,理由为:
∵EC⊥AB,DF⊥AB,
∴∠ADF=∠BCE=90°,
在△AFD和△BEC中,
∠A=∠B AD=BC ∠ADF=∠BCE ,
∴△AFD≌△BEC(ASA).
3、不一定 不一定 不一定 一定 一定 不一定 一定
【解析】(1)两边对应相等的两个三角形不一定全等;
(2)一边一角对应相等的两个三角形不一定全等;
(3)两角对应相等的两个三角形不一定全等;
(4)三边对应相等的两个三角形一定全等(根据SSS可判定全等);
(5)两边和它们的夹角对应相等的两个三角形一定全等(根据SAS可判定全等);
(6)两边和其中一边的对角对应相等的两个三角形不一定全等;
(7)两角和它们的夹边对应相等的两个三角形一定全等(根据ASA可判定全等);
4. ASA
【解析】
如图所示:
根据已知两角和它们的夹边相等得出全等三角形,
故答案为:ASA.
三、解答题
1.【解析】
证明 :∵AE⊥BF ∠BAP=∠AED
∴∠ABF=∠DAE
∵AB=AD ∠FAB=∠EDA
∴△ABF≌△ADE
∴AE=BF
2. 【解析】
证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BC=EF,
∵∠ACB=∠F,
∵∠B=∠DEF,BC=EF,∠ACB=∠F
∴△ABC≌△DEF。(ASA)
四、探究题
②∵△ABE≌△ACD,
∴∠ABE=∠ACD,
BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,
即△AMN为等腰三角形.
(2)解:(1)中的两个结论仍然成立.
(3)证明:在图②中正确画出线段PD,
由(1)同理可证△ABM≌△ACN,
∴∠CAN=∠BAM,
∴∠BAC=∠MAN.
又∵∠BAC=∠DAE,
∴∠MAN=∠DAE=∠BAC.
∴△AMN,△ADE和△ABC都是顶角相等的等腰三角形.
∴△PBD和△AMN都为顶角相等的等腰三角形,
∴∠PBD=∠AMN,∠PDB=∠ANM,
∴△PBD∽△AMN.
∴∠APB=∠MAN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
