1.5三角形全等的判定(2)练习题(含答案)
文档属性
| 名称 | 1.5三角形全等的判定(2)练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 428.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-12 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
三角形全等的判定(2)
班级:___________姓名:___________得分:__________
一、选择题
1、如图,在△ABC中,DE垂直平分AB,点E为垂足,FG垂直平分AC,点G为垂足,BC=5cm,则△ADF的周长等于( )21世纪教育网版权所有
A.4cm B.5cm C.6cm D.7cm
2. 如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
3. 在△ABC和△DEF中,已知AB=4cm,BC=6cm,∠B=60°,DE=6cm,DF=4cm,∠E+∠F=120°,则△ABC和△DEF的关系是( )21教育网
A.△ABC和△DEF不全等 B.△ABC≌△DEF
C.△ABC≌△FDE D.无法确定
4. 如图所示,梯形ABCD的对角线AC和BD相交于点O,OA=OD,AC=BD,则图中全等的三角形有( )21·cn·jy·com
A.1对 B.2对 C.3对 D.4对
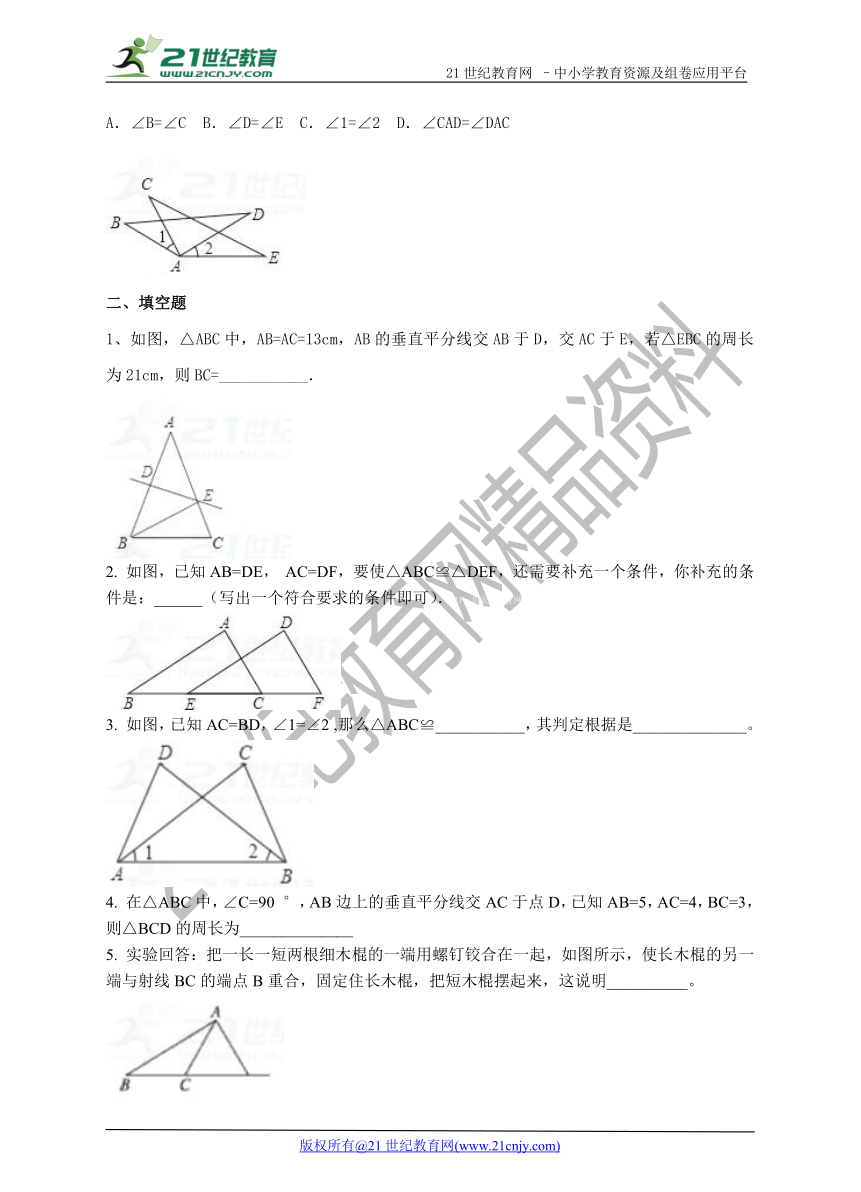
5. 如图,已知AB=AC,AD=AE,欲证△ABD≌△ACE,须补充的条件是( )
A.∠B=∠C B.∠D=∠E C.∠1=∠2 D.∠CAD=∠DAC
二、填空题
1、如图,△ABC中,AB=AC=13cm,AB的垂直平分线交AB于D,交AC于E,若△EBC的周长为21cm,则BC=___________.2·1·c·n·j·y
2. 如图,已知AB=DE, AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是:______(写出一个符合要求的条件即可).21·世纪*教育网
3. 如图,已知AC=BD,∠1=∠2 ,那么△ABC≌___________,其判定根据是______________。
4. 在△ABC中,∠C=90 °,AB边上的垂直平分线交AC于点D,已知AB=5,AC=4,BC=3,则△BCD的周长为______________【来源:21·世纪·教育·网】
5. 实验回答:把一长一短两根细木棍的一端用螺钉铰合在一起,如图所示,使长木棍的另一端与射线BC的端点B重合,固定住长木棍,把短木棍摆起来,这说明__________。
三、解答题
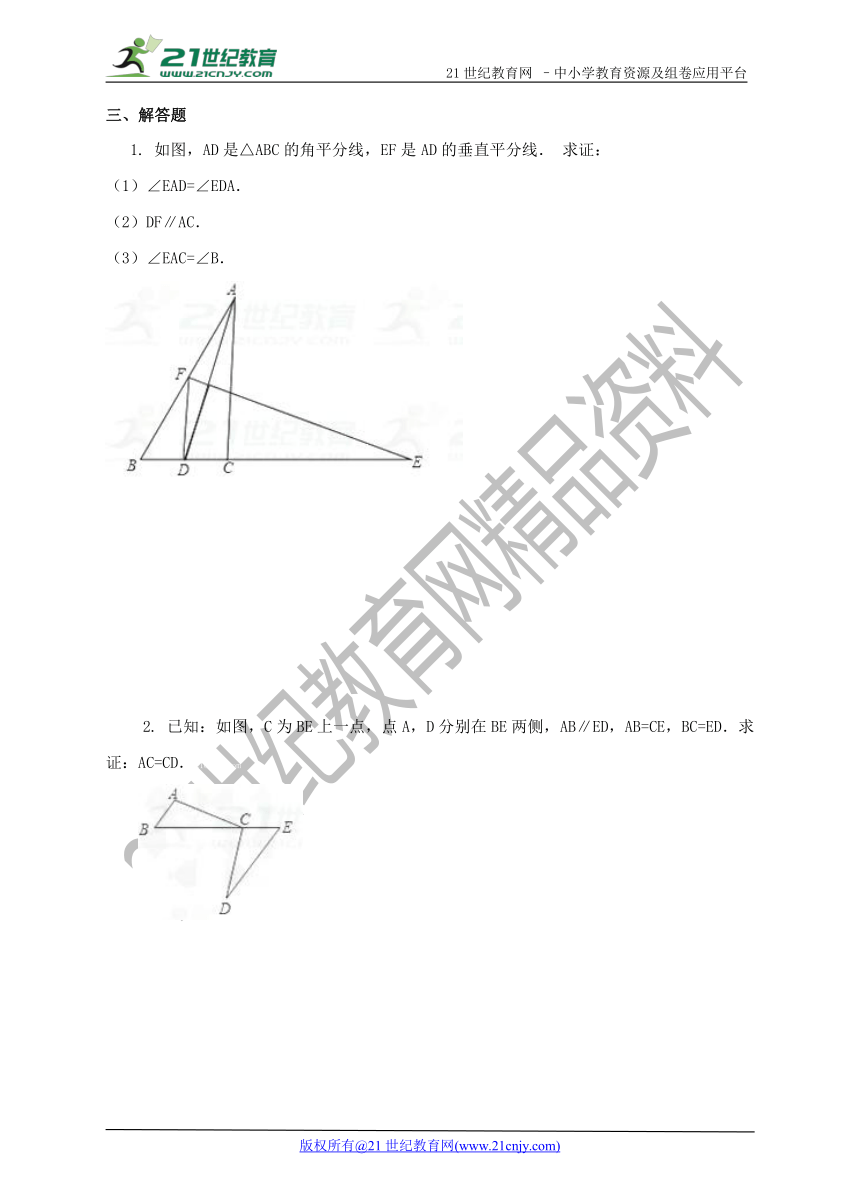
1. 如图,AD是△ABC的角平分线,EF是AD的垂直平分线. 求证:
(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
2. 已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.21cnjy.com
四、探究题
如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE,AE⊥CE,垂足分别为D、E,猜想图中线段DE、AE、DB之间的关系,并说明理由.www.21-cn-jy.com
参考答案
一、选择题
2、B
【解析】∵BC=BD+AD=BD+CD
∴AD=CD
∴点D在AC的垂直平分线上.
故选B.
3、C
【解析】∵∠E+∠F=120°,
∴∠D=60°,
在△BAC和△DFE中,
BA=DF ∠B=∠D BC=DE ,
∴△BAC≌△DFE(SAS).
故选C.
4.C
【解析】∵OA=OD,AC=BD,
∴OC=OB,∠AOB=∠DOC,
∴△ABO≌△DCO(SAS),∠OBC=∠OCB,
∴梯形ABCD为等腰梯形,
∴AB=DC,∠BAD=∠CDA,
∴△ABC≌△DCB(SAS),
△ABD≌△DCA(SAS);
∴图中全等的三角形有3对.
故选C.
5.C
【解析】∵AB=AC,AD=AE,
∠B=∠C不是已知两边的夹角,A不可以;
∠D=∠E不是已知两边的夹角,B不可以;
由∠1=∠2得∠BAD=∠CAE,符合SAS,可以为补充的条件;
∠CAD=∠DAC不是已知两边的夹角,D不可以;
故选C.
二、填空题
1、8cm
【解析】∵AB的垂直平分线交AB于D,
∴AE=BE
又△EBC的周长为21cm,
即BE+CE+BC=21
∴AE+CE+BC=21
又AE+CE=AC=13cm
所以BC=21-13=8cm.
2、∠A=∠D
【解析】∠A=∠D,
理由是:∵在△ABC和△DEF中,
AB=DE ∠A=∠D AC=DF ,
∴△ABC≌△DEF(SAS),
故答案为:∠A=∠D.
3、△BAD,SAS
【解析】在△ABC和△BAD中,
AC=BD
∠1=∠2
AB=BA(公共边)
所以,△ABC≌△BAD(SAS).
故答案为:△BAD,SAS.
4.7
【解析】解:如图,
∵DE是AB的垂直平分线,
∴BD=AD,
∴BD+CD=AD+CD=AC,
又∵C△BDC=BC+BD+CD=BC+AC,
∵BC=3,AC=4,
∴C△BDC=3+4=7.
故答案为:7.
5. 两边及其一边的对角对应相等,两个三角形不一定全等
【解析】由题意可知,两边及其一边的对角对应相等,两个三角形不一定全等
三、解答题
1.【解析】证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠BAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC;
(3)由(1)∠EAD=∠EDA,即∠ADE=∠CAD+∠EAC,
∵∠ADE=∠BAD+∠B,∠BAD=∠CAD,
∴∠EAC=∠B.
2. 【解析】证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
AB=CE,∠B=∠E,BC=ED
∴△ABC≌△CED.
∴AC=CD.
四、应用题
【解析】解:DE+AE=DB
∵∠ACB=90°,BD⊥CE
∴∠ACE+∠ECB=90°,
∠ECB+∠CBD=90°
∴∠ACE=∠CBD
又∵AE⊥CE
∴∠AEC=90°
在Rt△AEC和Rt△CDB中
AC=BC,∠AEC=∠CDB=90°,∠ACE=∠CBD
∴Rt△AEC≌Rt△CDB
∴AE=CD,EC=DB
又∵DE+DC=EC
∴DE+AE=DB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
三角形全等的判定(2)
班级:___________姓名:___________得分:__________
一、选择题
1、如图,在△ABC中,DE垂直平分AB,点E为垂足,FG垂直平分AC,点G为垂足,BC=5cm,则△ADF的周长等于( )21世纪教育网版权所有
A.4cm B.5cm C.6cm D.7cm
2. 如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上.
A.AB B.AC C.BC D.不能确定
3. 在△ABC和△DEF中,已知AB=4cm,BC=6cm,∠B=60°,DE=6cm,DF=4cm,∠E+∠F=120°,则△ABC和△DEF的关系是( )21教育网
A.△ABC和△DEF不全等 B.△ABC≌△DEF
C.△ABC≌△FDE D.无法确定
4. 如图所示,梯形ABCD的对角线AC和BD相交于点O,OA=OD,AC=BD,则图中全等的三角形有( )21·cn·jy·com
A.1对 B.2对 C.3对 D.4对
5. 如图,已知AB=AC,AD=AE,欲证△ABD≌△ACE,须补充的条件是( )
A.∠B=∠C B.∠D=∠E C.∠1=∠2 D.∠CAD=∠DAC
二、填空题
1、如图,△ABC中,AB=AC=13cm,AB的垂直平分线交AB于D,交AC于E,若△EBC的周长为21cm,则BC=___________.2·1·c·n·j·y
2. 如图,已知AB=DE, AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是:______(写出一个符合要求的条件即可).21·世纪*教育网
3. 如图,已知AC=BD,∠1=∠2 ,那么△ABC≌___________,其判定根据是______________。
4. 在△ABC中,∠C=90 °,AB边上的垂直平分线交AC于点D,已知AB=5,AC=4,BC=3,则△BCD的周长为______________【来源:21·世纪·教育·网】
5. 实验回答:把一长一短两根细木棍的一端用螺钉铰合在一起,如图所示,使长木棍的另一端与射线BC的端点B重合,固定住长木棍,把短木棍摆起来,这说明__________。
三、解答题
1. 如图,AD是△ABC的角平分线,EF是AD的垂直平分线. 求证:
(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
2. 已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.21cnjy.com
四、探究题
如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE,AE⊥CE,垂足分别为D、E,猜想图中线段DE、AE、DB之间的关系,并说明理由.www.21-cn-jy.com
参考答案
一、选择题
2、B
【解析】∵BC=BD+AD=BD+CD
∴AD=CD
∴点D在AC的垂直平分线上.
故选B.
3、C
【解析】∵∠E+∠F=120°,
∴∠D=60°,
在△BAC和△DFE中,
BA=DF ∠B=∠D BC=DE ,
∴△BAC≌△DFE(SAS).
故选C.
4.C
【解析】∵OA=OD,AC=BD,
∴OC=OB,∠AOB=∠DOC,
∴△ABO≌△DCO(SAS),∠OBC=∠OCB,
∴梯形ABCD为等腰梯形,
∴AB=DC,∠BAD=∠CDA,
∴△ABC≌△DCB(SAS),
△ABD≌△DCA(SAS);
∴图中全等的三角形有3对.
故选C.
5.C
【解析】∵AB=AC,AD=AE,
∠B=∠C不是已知两边的夹角,A不可以;
∠D=∠E不是已知两边的夹角,B不可以;
由∠1=∠2得∠BAD=∠CAE,符合SAS,可以为补充的条件;
∠CAD=∠DAC不是已知两边的夹角,D不可以;
故选C.
二、填空题
1、8cm
【解析】∵AB的垂直平分线交AB于D,
∴AE=BE
又△EBC的周长为21cm,
即BE+CE+BC=21
∴AE+CE+BC=21
又AE+CE=AC=13cm
所以BC=21-13=8cm.
2、∠A=∠D
【解析】∠A=∠D,
理由是:∵在△ABC和△DEF中,
AB=DE ∠A=∠D AC=DF ,
∴△ABC≌△DEF(SAS),
故答案为:∠A=∠D.
3、△BAD,SAS
【解析】在△ABC和△BAD中,
AC=BD
∠1=∠2
AB=BA(公共边)
所以,△ABC≌△BAD(SAS).
故答案为:△BAD,SAS.
4.7
【解析】解:如图,
∵DE是AB的垂直平分线,
∴BD=AD,
∴BD+CD=AD+CD=AC,
又∵C△BDC=BC+BD+CD=BC+AC,
∵BC=3,AC=4,
∴C△BDC=3+4=7.
故答案为:7.
5. 两边及其一边的对角对应相等,两个三角形不一定全等
【解析】由题意可知,两边及其一边的对角对应相等,两个三角形不一定全等
三、解答题
1.【解析】证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠BAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC;
(3)由(1)∠EAD=∠EDA,即∠ADE=∠CAD+∠EAC,
∵∠ADE=∠BAD+∠B,∠BAD=∠CAD,
∴∠EAC=∠B.
2. 【解析】证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
AB=CE,∠B=∠E,BC=ED
∴△ABC≌△CED.
∴AC=CD.
四、应用题
【解析】解:DE+AE=DB
∵∠ACB=90°,BD⊥CE
∴∠ACE+∠ECB=90°,
∠ECB+∠CBD=90°
∴∠ACE=∠CBD
又∵AE⊥CE
∴∠AEC=90°
在Rt△AEC和Rt△CDB中
AC=BC,∠AEC=∠CDB=90°,∠ACE=∠CBD
∴Rt△AEC≌Rt△CDB
∴AE=CD,EC=DB
又∵DE+DC=EC
∴DE+AE=DB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
