1.6尺规作图 练习题（含答案）

21世纪教育网 –中小学教育资源及组卷应用平台
尺规作图
班级：___________姓名：___________得分：__________
一、选择题
1、下列尺规作图的语句正确的是（　）
A．延长射线AB到点C
B．延长直线AB到点C
C．延长线段AB到点C，使BC=AB
D．延长线段AB到点C，使AC=BC
2. 如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：21教育网
（1）作线段BC=a；
（2）作线段BC的垂直平分线MN，MN与BC相交于点D；
（3）在直线MN上截取线段h；
（4）连接AB，AC，△ABC为所求的等腰三角形．
上述作法的四个步骤中，有错误的一步你认为是（　）
A．（1） B．（2） C．（3） D．（4）
3. 如图，点C落在∠AOB边上，用尺规作CN∥OA，其中弧FG的（　　）
A．圆心是C，半径是OD
B．圆心是C，半径是DM
C．圆心是E，半径是OD
D．圆心是E，半径是DM21·cn·jy·com
4. 下列作图属于尺规作图的是（　）
A．画线段MN=3cm
B．用量角器画出∠AOB的平分线
C．用三角尺作过点A垂直于直线L的直线
D．已知∠α，用没有刻度的直尺和圆规作∠AOB，使∠AOB=2∠α
5. 如图，已知线段AB，以下作图不可能的是（　　）
A. 在AB上取一点C，使AC=BC
B. 在AB的延长线上取一点C，使BC=AB
C. 在BA的延长线上取一点C，使BC=AB
D. 在BA的延长线上取一点C，使BC=2AB
二、填空题
1、作线段的垂直平分线的理论根据是______________和两点确定一条直线。
2. 已知∠A和线段AB，要作一个唯一的△ABC，还需给出一个条件是______．
3. 已知底边a和底边上的高h，在用尺规作图方法作这个等腰△CDE，使DE=a，CB=h时，需用到的作法有：21世纪教育网版权所有
①在MN上截取BC=h；②作线段DE=a；③作线段DE的垂直平分线MN，与DE交于点B；④连接CD，CE，△CDE就是所求的等腰三角形．www.21-cn-jy.com
则正确作图步骤的序号是______．
4. 根据图形把下列画图语句补充完整。
（1）如图1所示，在__________上截取_______________=a ；
（2）如图2所示，以点___________为圆心，以_______为半径作弧，交__________于点________。【来源：21·世纪·教育·网】
5. 画线段AB；延长线段AB到点C，使BC=2AB；反向延长AB到点D，使AD=AC，则线段CD=______AB．21cnjy.com
三、作图题
1. 读下面的语句，并画图形．
（1）P是直线AB外的一点，直线CD经过点P，且与直线AB平行；直线EF经过点P，且与AB垂直，垂足为点G；
（2）直线AB、CD是相交直线，点P是直线AB．CD外的一点，直线EF经过点P，且与直线AB平行，与直线CD相交于E．21·世纪*教育网
2. 如图，铁路OA和公路OB在我市相交于点O，在∠AOB的内部有工厂C和D，现要修建一个货物站P，要求P到OA、OB的距离相等，且PC=PD，请确定出点P的位置．（用尺规作图，不写作法，但要保留痕迹）2·1·c·n·j·y
四、探究题
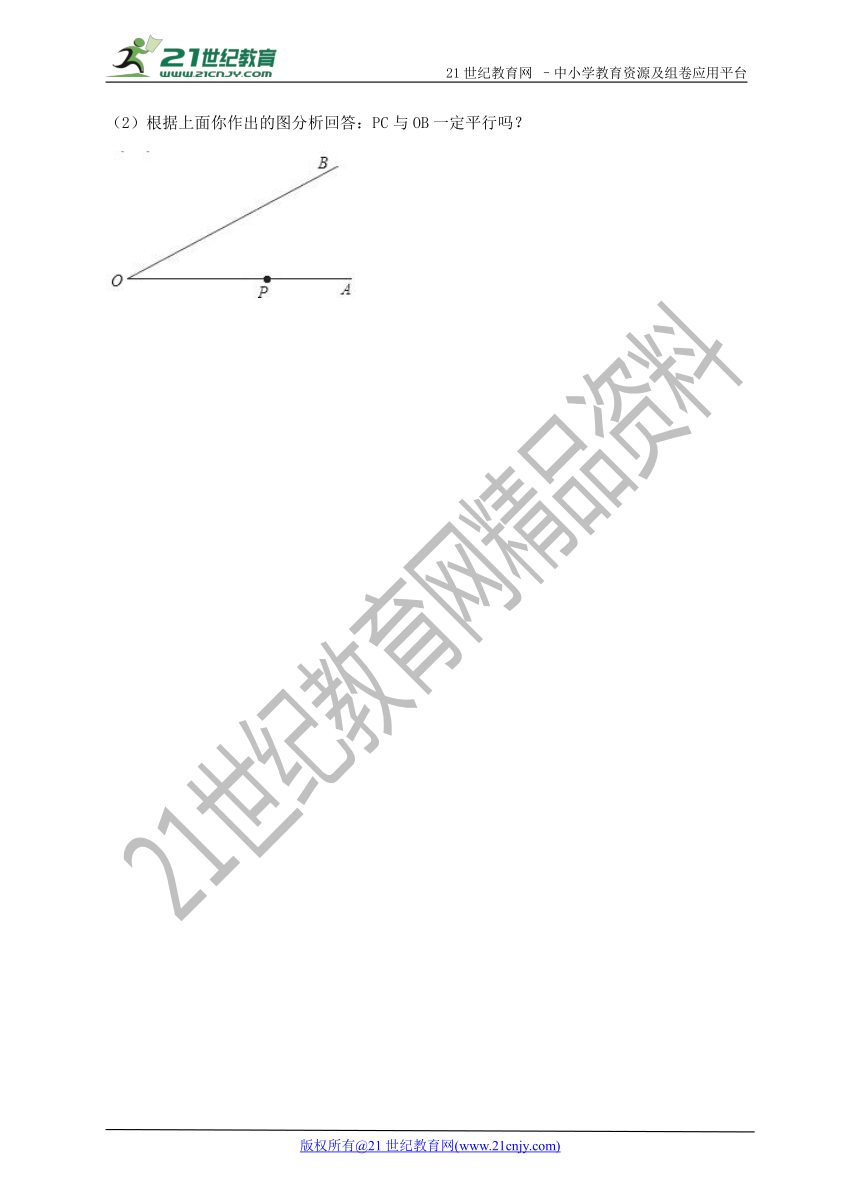
如图：（1）已知：∠AOB，点P在OA上，请以P为顶点，PA为一边作∠APC=∠O；（用尺规作图，不写作法，保留作图痕迹）2-1-c-n-j-y
（2）根据上面你作出的图分析回答：PC与OB一定平行吗？
参考答案
一、选择题
2、C
【解析】（3）在直线MN上截取线段h，带有随意性，与作图语言的准确性不相符．
3、D
【解析】图中要作CN∥OA，就是作∠NCB=∠AOD，
根据作一个角等于已知角的方法可得弧FG是以圆心是E，半径是DM所画的弧．
故选：D．
4.D
【解析】A、画线段MN=3cm，需要知道长度，而尺规作图中的直尺是没有长度的，错误；
B、用量角器画出∠AOB的平分线，量角器不在尺规作图的工具里，错误；
C、用三角尺作过点A垂直于直线L的直线，三角尺也不在作图工具里，错误；
D、正确．
故选D．
5.C
【解析】A、可能，只要做AB的垂直平分线即可；
B、可能，在AB的延长线上取一点C，使BC=AB；
C、不可能，因为BC始终大于AB；
D、可能，在BA的延长线上取一点C，使BC=2AB．
故选C．
二、填空题
1、到线段两端点距离相等的点,在这条线段的垂直平分线上
【解析】画垂直平分线的依据就是垂直平分线的性质，即到线段两端点距离相等的点,在这条线段的垂直平分线上www-2-1-cnjy-com
2、AC（或∠B）
【解析】因为全等三角形的判定有SAS，ASA，所以还需给出的条件是：已知AC（或∠B）．
3、②③①④
【解析】首先作线段DE=a；
然后作线段DE的垂直平分线MN，与DE交于点B；
再在MN上截取BC=h；
最后连接CD，CE，△CDE就是所求的等腰三角形，
故答案为：②③①④．
4. （1）射线OM，OA；（2）A，R，射线AB，M
【解析】根据作图的步骤，可知应该填（1）射线OM，OA；（2）A，R，射线AB，M
5. 6
【解析】（1）画线段AB；
（2）延长线段AB到点C，使BC=2AB；
（3）反向延长AB到点D，使AD=AC；
由图可知，BC=2AB，AD=AC=3AB，故CD=6AB．21*cnjy*com
【】
三、作图题
1.【解析】（1）如图所示：
（2）如图所示：
2. 【解析】作∠AOB的平分线、线段CD的垂直平分线，两线的交点就是所求．
四、探究题
【解析】（1）以∠O的顶点为圆心，以任意长为半径画弧，交∠O的两边于两点；以点P为圆心，刚才的半径为半径，交射线PA于一点，以这点为圆心，∠O两边上两点的距离为半径画弧，交前弧于一点，过这点作射线OC，∠APC，∠APC′就是所求的角；
（2）由（1）作出的图形可得PC与OB不一定平行．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)