八年级上册(浙教版)数学第一章三角形的初步知识 单元检测试卷(含答案)
文档属性
| 名称 | 八年级上册(浙教版)数学第一章三角形的初步知识 单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 212.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-24 16:31:05 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
八年级上册(浙教版)数学第一单元检测试卷
数学考试
姓名:__________
班级:__________考号:__________
题号
一
二
三
四
五
六
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前
xx
分钟收取答题卡
第Ⅰ卷
客观题
第Ⅰ卷的注释
一、单选题(共10题;共20分)
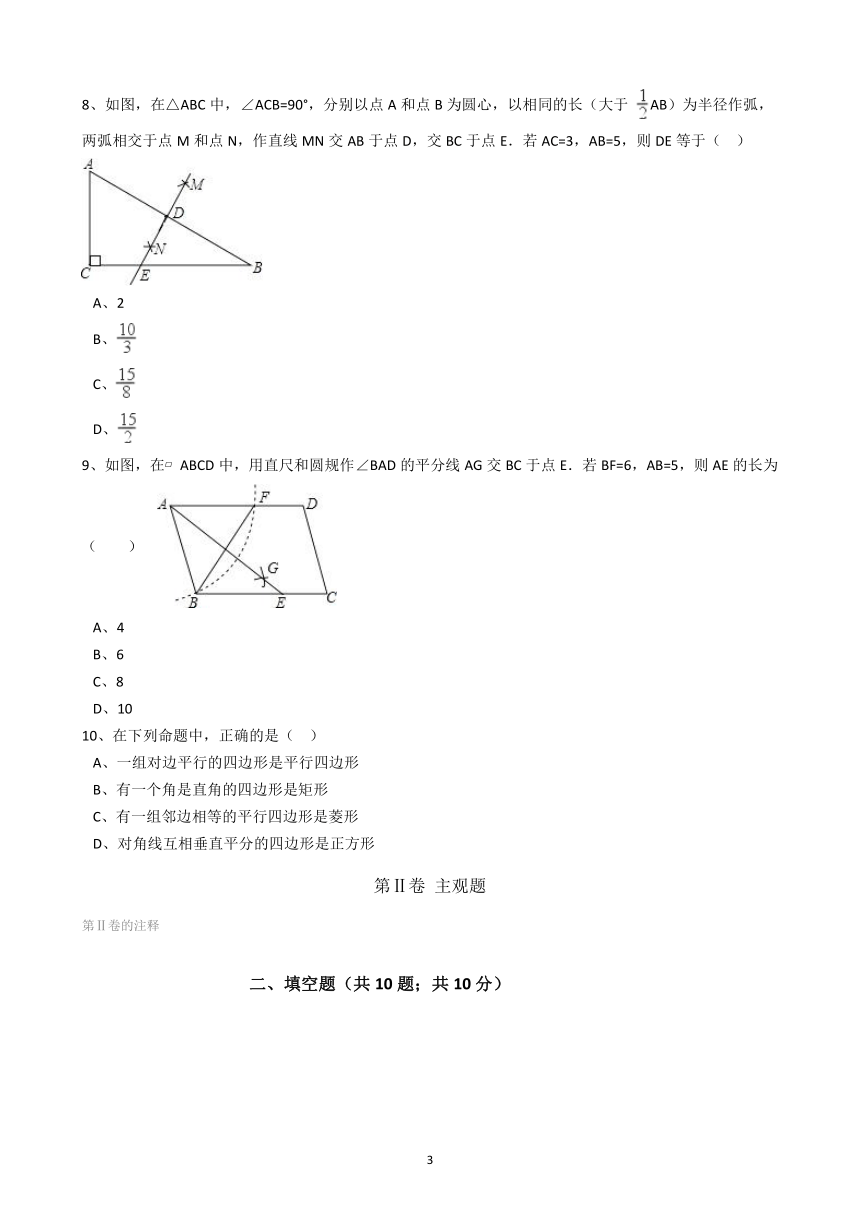
1、如图,已知在
中,
,
,
,点
是
的重心,则点
到
所在直线的距离等于(
)
A、
B、
C、
D、
2、如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是(
)
A、B、C、D、
3、如图,等腰三角形ABC中,AB=AC,BD是AC边上的高,若∠A=36°,则∠DBC的大小是(
)
A、18°
B、36°
C、54°
D、72°
4、如图,
,垂足为D,
,下列说法正确的是(
)
A、射线AC是
的角平分线
B、直线BD是
的边AD上的高
C、线段AC是
的中线
D、线段AD是
的边BC上的高
5、下列命题中,为真命题的是(
)
A、如果-2x>-2,那么x>1
B、如果a2=b2,那么a3=b3
C、面积相等的三角形全等
D、如果a∥b,b∥c,那么a∥c
6、下列命题中,错误的是(
).
A、平行四边形的对角线互相平分
B、菱形的对角线互相垂直平分
C、矩形的对角线相等且互相垂直平分
D、角平分线上的点到角两边的距离相等
7、如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数(
)
A、1对
B、2对
C、3对
D、4对
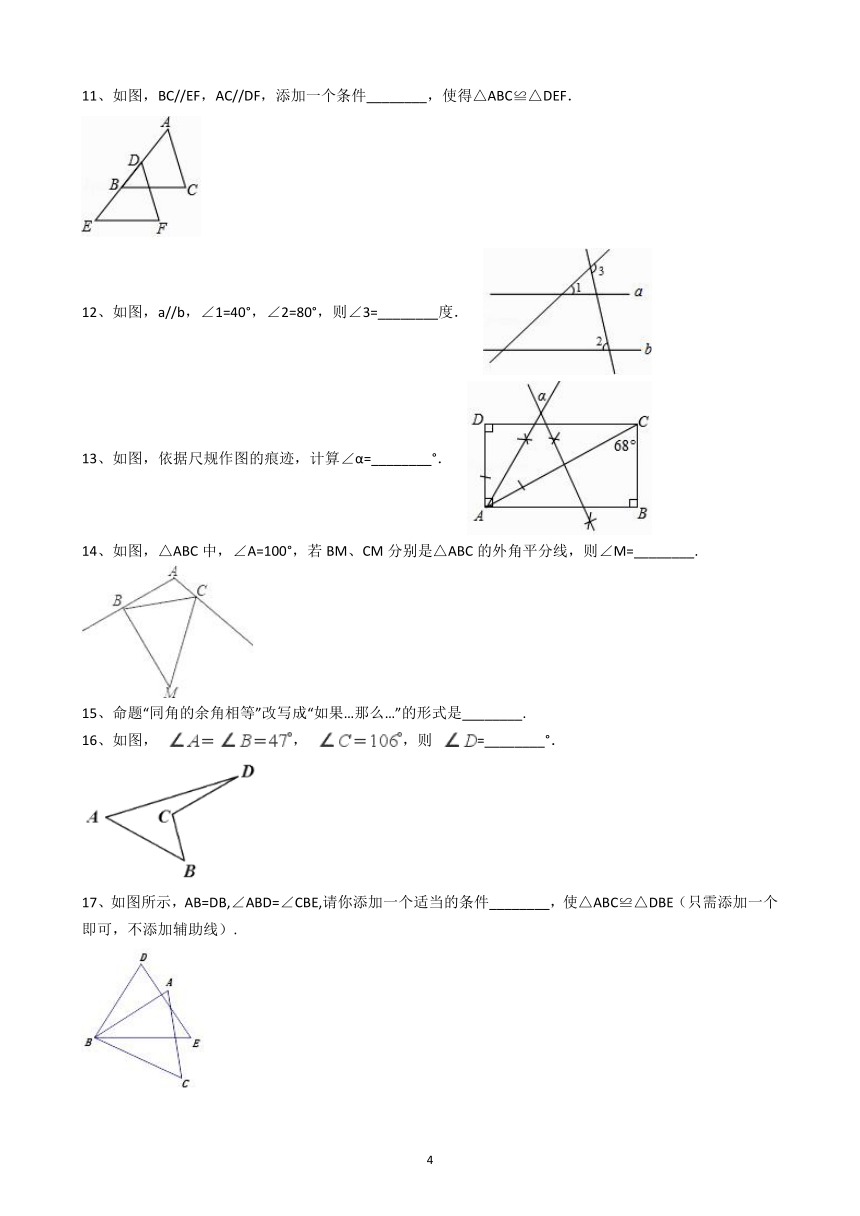
8、如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于(
)
A、2
B、
C、
D、
9、如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )
A、4
B、6
C、8
D、10
10、在下列命题中,正确的是(
)
A、一组对边平行的四边形是平行四边形
B、有一个角是直角的四边形是矩形
C、有一组邻边相等的平行四边形是菱形
D、对角线互相垂直平分的四边形是正方形
第Ⅱ卷
主观题
第Ⅱ卷的注释
二、填空题(共10题;共10分)
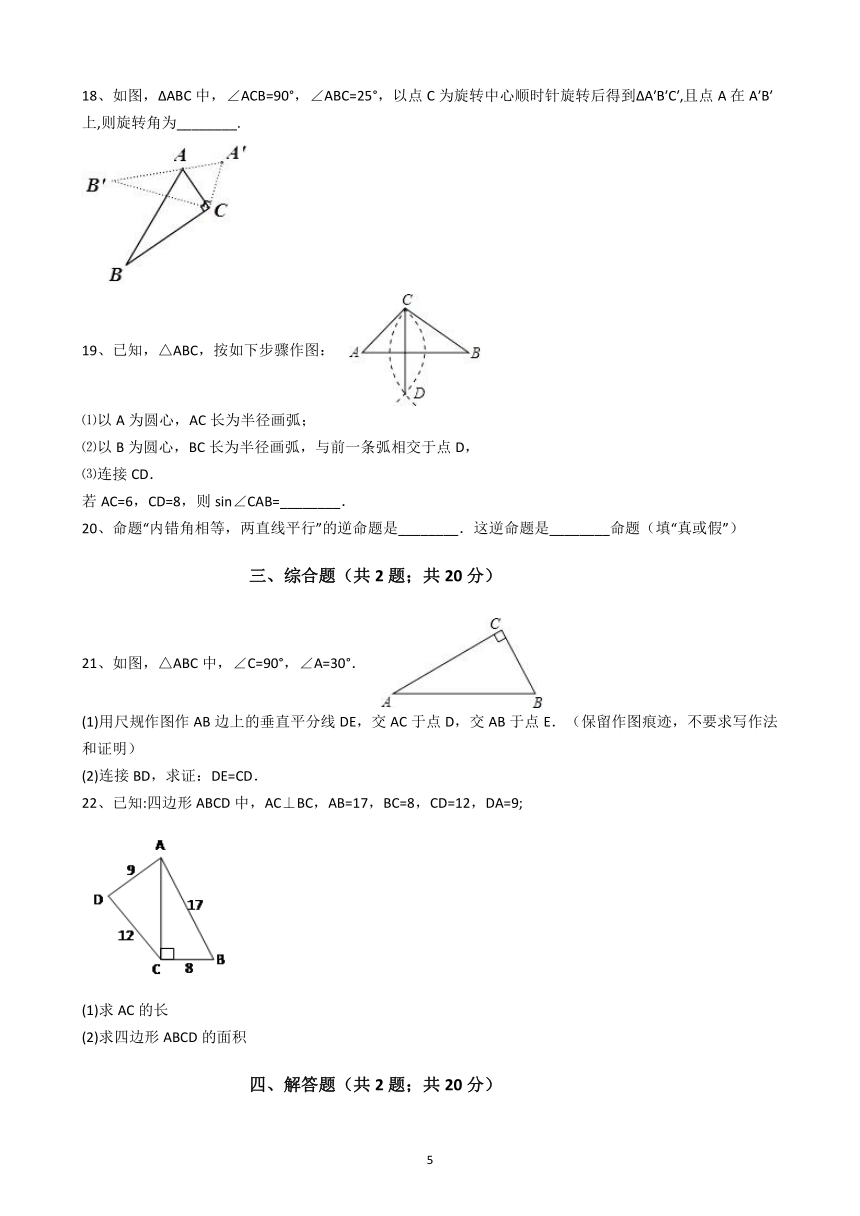
11、如图,BC//EF,AC//DF,添加一个条件________,使得△ABC≌△DEF.
12、如图,a//b,∠1=40°,∠2=80°,则∠3=________度.
13、如图,依据尺规作图的痕迹,计算∠α=________°.
14、如图,△ABC中,∠A=100°,若BM、CM分别是△ABC的外角平分线,则∠M=________.
15、命题“同角的余角相等”改写成“如果…那么…”的形式是________.
16、如图,
,
,则
=________°.
17、如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件________,使△ABC≌△DBE(只需添加一个即可,不添加辅助线).
18、如图,ΔABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到ΔA′B′C′,且点A在A′B′上,则旋转角为________.
19、已知,△ABC,按如下步骤作图:
⑴以A为圆心,AC长为半径画弧;
⑵以B为圆心,BC长为半径画弧,与前一条弧相交于点D,
⑶连接CD.
若AC=6,CD=8,则sin∠CAB=________.
20、命题“内错角相等,两直线平行”的逆命题是________.这逆命题是________命题(填“真或假”)
三、综合题(共2题;共20分)
21、如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
22、已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9;
(1)求AC的长
(2)求四边形ABCD的面积
四、解答题(共2题;共20分)
23、如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么?
24、如图,在△ABC中,AB
=AC,BD⊥AC,CE⊥AB,求证:BD=CE.
五、计算题(共5题;共25分)
25、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.
26、如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠B=24°,∠C=44°.求:∠DAE的度数.
27、已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,求∠B的度数.
28、如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
29、如图,∠A=65°,∠ABD=30°,∠ACB=72°,且CE平分∠ACB,求∠BEC的度数.
六、作图题(共1题;共5分)
30、作图题(尺规作图,不写作法,保留作图痕迹)
“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图),准备建立一个燃气中心站P
,
使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.
答案解析部分
一、单选题
1、【答案】A
【考点】全等三角形的判定与性质,相似三角形的判定与性质,等腰直角三角形
【解析】【解答】解:如图,连接CP并延长交AB于D,连接BP交AC于E,并延长到F,使EF=PE,
∵∠C=90°,AC=BC,AB=6,
∴AC=BC=3,
又∵P为△ABC的重心,
∴CD=AB=3.∠CDB=90°
在△AEF和△CEP中,
∵
∴△AEF≌△CEP.
∴∠FAD=90°,CP=AF=3-DP.
又∵CD‖FA,
∴△BPD∽△BFA.
∴=.
∴=.
∴PD=1.
故答案为A.
【分
析】如图,根据三角形的重心是三条中线的交点,根据等腰直角三角形可知CD=3,可连接CP并延长交AB于D,则∠FAD=90°,连接BP交AC于E,
并延长到F,使EF=PE,然后可知△A,可得EF≌△CEP,∠FAD=90°,CP=AF=3-DP,因此可根据两角对应相等的两三角形相似,可得
△BPD∽△BFA.即可求出PD.
2、【答案】A
【考点】三角形三边关系,正方形的性质
【解析】【解答】解:选项A不正确.理由正方形的边长为10,所以对角线=10
≈14,
因为15>14,所以这个图形不可能存在.
故选A.
【分析】利用勾股定理求出正方形的对角线为10
≈14,由此即可判定A不正确.
3、【答案】A
【考点】三角形内角和定理,等腰三角形的性质
【解析】【解答】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°
∵BD是AC边上的高,
∴BD⊥AC,
∴∠ADB=90°,
∴∠DBC=90°-72°=18°.
故选A.
4、【答案】D
【考点】三角形的角平分线、中线和高
【解析】【解答】解:三角形的角平分线、高线均为线段,故A、B错误;
线段AC是
的角平分线,故C错误;
由
可知,线段AD是
的边BC上的高,故D正确.
故选D.
5、【答案】D
【考点】命题与定理
【解析】【解答】解:A项如果-2x>-2,那么x<1,故为假命题;
B项当a与b的符号不同时,a2=b2时,a2≠b2
,
故为假命题;
C项由于“面积相等的三角形全等”的逆否命题“不全等的三角形面积不相等”显然为假,故为假命题.
D项平行于同一直线的两条直线平行,故为真命题,
故选D.
【分析】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫假命题.
判断命题的真假关键是要熟悉课本中的性质定理.
6、【答案】C
【考点】角平分线的性质,平行四边形的性质,菱形的性质,矩形的性质,命题与定理
【解析】【解答】解:A.根据平行四边形的性质可得,平行四边形的对角线互相平分,故A正确;
B.根据菱形的性质可得,菱形的对角线互相垂直平分,故B正确;
C.根据矩形的性质可得,矩形的对角线相等且互相平分,而不一定垂直,故C错误;
D.根据角平分线的性质可得,角平分线上的点到角的两边距离相等,故D正确
故选:C.
7、【答案】D
【考点】全等三角形的判定,平行四边形的性质
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).
8、【答案】C
【考点】线段垂直平分线的性质,勾股定理,作图—基本作图
【解析】【解答】解:在Rt△ACB中,由勾股定理得:BC=
=4,
连接AE,
从作法可知:DE是AB的垂直平分线,
根据性质得出AE=BE,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2
,
即32+(4﹣AE)2=AE2
,
解得:AE=
,
在Rt△ADE中,AD=
AB=
,由勾股定理得:DE2+(
)2=(
)2
,
解得:DE=
.
故选C.
【分析】根据勾股定理求出BC,根据线段垂直平分线性质求出AE=BE,根据勾股定理求出AE,再根据勾股定理求出DE即可.
9、【答案】C
【考点】等腰三角形的判定与性质,勾股定理,平行四边形的性质,作图—基本作图
【解析】【解答】解:连结EF,AE与BF交于点O,如图,
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=
BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=
=
=4,
∴AE=2AO=8.
故选C.
【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=
BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
10、【答案】C
【考点】命题与定理
【解析】【解答】解:A、应为两组对边平行的四边形是平行四边形;
B、有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;
C、符合菱形定义;
D、应为对角线互相垂直平分且相等的四边形是正方形.
故选:C.
【分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.两组对边平行的四边形是平行四边形;有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;有一组邻边相等的平行四边形是菱形;对角线互相垂直平分且相等的四边形是正方形.
二、填空题
11、【答案】AB=DE或BC=EF或AC=DF
【考点】全等三角形的判定
【解析】【解答】解:∵BC//EF,
∴∠ABC=∠E,
∵AC//DF,
∴∠A=∠EDF,
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF,
同理,BC=EF或AC=DF也可求证△ABC≌△DEF.
故答案为AB=DE或BC=EF或AC=DF均可.
【分析】本题要判定△ABC≌△DEF,易证∠A=∠EDF,∠ABC=∠E,故添加AB=DE、BC=EF或AC=DF根据ASA、AAS即可解题.
12、【答案】120
【考点】平行线的性质,三角形的外角性质
【解析】【解答】解:如图,∵a//b,∠2=80°,
∴∠4=∠2=80°(两直线平行,同位角相等)
∴∠3=∠1+∠4=40°+80°=120°.
故答案为120°.
【分析】先根据两直线平行,同位角相等,求出∠2的同位角的度数,再利用三角形的外角的性质求得∠3的度数.
13、【答案】56
【考点】作图—基本作图
【解析】【解答】解:∵四边形ABCD的矩形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=
∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°﹣34°=56°,
∴∠α=56°.
故答案为:56.
【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.
14、【答案】40°
【考点】角平分线的定义,三角形内角和定理,三角形的外角性质
【解析】【解答】解:∵∠A=100°,
∴∠ABC+∠ACB=180° ∠A=80°,
∴∠DBC+∠ECB=180° ∠ABC+180° ∠ACB=360° (∠ABC+∠ACB)=360° 80°=280°,
∵BM、CM分别平分∠DBC和∠ECB,
∴∠MBC+∠MCB=
(∠DBC+∠ECB)=
×280°=140°,
∴∠M=180° (∠OBC+∠OCB)=180° 140°=40°,
故答案为:40°.
15、【答案】如果两个角是同一个角的余角,那么这两个角相等.
【考点】命题与定理
【解析】【解答】解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
16、【答案】
【考点】三角形的外角性质
【解析】【解答】解:连接AC并延长,标注点E,
∵∠DCE=∠D+∠DAC,
∠BCE=∠B+∠BAC,
∠BCE+∠DCE=106°,∠A=∠B=47°,
∴∠BCE+∠DCE=∠D+∠DAB+∠B=106°,
∴∠D=106°-47°-47°=12°.
故答案为:12.
【分析】利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.
17、【答案】∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可).
【考点】全等三角形的判定
【解析】【解答】解:∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠ABC=∠DBE,
∵AB=DB,
∴①用“角边角”,需添加∠BDE=∠BAC,
②用“边角边”,需添加BE=BC,
③用“角角边”,需添加∠ACB=∠DEB.
18、【答案】50°
【考点】三角形内角和定理,全等三角形的性质,旋转的性质
【解析】【解答】解:∵将△ACB绕点C顺时针旋转得到
,
∴△ACB≌
,
∴∠A′=∠BAC,AC=CA′,
∴∠A′=∠CAA′,
∴∠CAA′=∠BAC.
∵△ACB中,∠ACB=90°,∠ABC=25°,
∴∠BAC=90 ∠ABC=65°,
∴∠BAC=∠CAA′=65°,
∴∠B′AB=180° 65° 65°=50°,
∴∠ACB′=180° 25° 50° 65°=40°,
∴∠B′CB=90° 40°=50°.
故答案为:50°.
19、【答案】
【考点】作图—基本作图,解直角三角形
【解析】【解答】解:如图,连接AD、BD.AB与CD交于点O.
∵AC=AD,BC=BD,
∴AB垂直平分线段CD,
∴CO=OD=4,
在Rt△AOC中,∵∠AOC=90°,AC=6,CO=4,
∴sin∠ACB=
=
=
.
故答案为
.
【分析】如图,连接AD、BD.AB与CD交于点O.首先证明AB垂直平分线段CD,根据sin∠ACB=
,即可解决问题.
20、【答案】两直线平行,内错角相等;真
【考点】命题与定理
【解析】【解答】解:“内错角相等,两直线平行”的逆命题是“两直线平行,内错角相等”,
它是真命题,
故答案为:两直线平行,内错角相等;真.
【分析】写出原命题的逆命题,根据平行线的性质判断即可.
三、综合题
21、【答案】(1)解:如图,DE为所作;
(2)证明:如图,
∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=30°,
即BD平分∠ABC,
而DE⊥AB,DC⊥BC,
∴DE=DC.
【考点】线段垂直平分线的性质,含30度角的直角三角形,作图—基本作图
【解析】【分析】(1)利用基本作图(作已知线段的垂直平分线)作DE垂直平分AB;(2)先利用线段垂直平分线的性质得到DA=DB,则∠DBA=∠A=30°,再证明BD平分∠ABC,然后根据角平分线的性质定理可得到结论.
22、【答案】(1)解:∵∠ACB=90°
∴AC2=AB2-BC2=172-82=225
∴AC=15
(2)解:∵AD2+CD2=92+122=225=AC2
∴∠D=90°
∴S四边形ABCD=
S△ABC+
S△ACD=
8×15÷2+12×9÷2=114.
【考点】三角形的面积,勾股定理,勾股定理的逆定理
【解析】【分析】(1)根据勾股定理可求AC的长;
(2)根据勾股定理的逆定理可判断∠D=90°,四边形ABCD的面积=△ABC的面积+△ADC的面积.
四、解答题
23、【答案】解:相等;
证明:在△ABC和△ADC中
∴△ABC≌△ADC(ASA),
∴BC=DC,
在△BEC和△DEC中
,
∴△BEC≌△DEC(SAS),
∴BE=DE
【考点】全等三角形的判定与性质
【解析】【分析】先证△ABC≌△ADC(ASA),再证△BEC≌△DEC(SAS),根据全等三角形的对应边相等可以得到BE=DE.
24、【答案】证明:∵BD⊥AC,CE⊥AB.
∴∠ADB=∠AEC=90°.
在△ABD和△ACE中.
∴△ABD≌△AEC(AAS)
∴BD=CE.
【考点】全等三角形的判定与性质
【解析】【分析】根据BD⊥AC,CE⊥AB,得出∠ADB=∠AEC=90°.再根据三角形全等的判定ASA得出△ABD≌△AEC;再根据全等三角形的性质得出BD=CE.
五、计算题
25、【答案】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=6,
∴DB=AB﹣AD=6﹣4=2
【考点】平行线的性质,全等三角形的判定与性质
【解析】【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=6,FC=4,即可求线段DB的长.
26、【答案】解:∵△ABC中,∠B=24°,∠C=44°
∴∠BAC=180°﹣∠B﹣∠C=112°,
∵AE是∠BAC的平分线,
∴∠EAC=
∠BAC=56°,
∵AD是BC边上的高,
∴在直角△ADC中,∠DAC=90°﹣∠C=90°﹣44°=46°,
∴∠DAE=∠EAC﹣∠DAC=56°﹣46°=10°.
【考点】三角形的角平分线、中线和高,三角形内角和定理
【解析】【分析】根据三角形的内角和定理,可求得∠BAC的度数,由AE是∠BAC的平分线,可得∠EAC的度数,在直角△ADC中,可求出∠DAC的度数,根据∠DAE=∠EAC﹣∠DAC,即可得出结论.
27、【答案】解:∵∠A=30°,
∴∠B+∠C=180°﹣∠A=150°,
∵∠C=2∠B,
∴3∠B=150°,
∴∠B=50°.
【考点】三角形内角和定理
【解析】【分析】根据三角形内角和定理求出∠B+∠C的度数,把∠C=2∠B代入求出即可.
28、【答案】解:∵在△ABC中,∠A=62°,
∴∠ABC+∠ACB=180°﹣62°=118°.
∵∠1=20°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=118°﹣20°﹣35°=63°.
∴∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣63°=117°.
【考点】三角形内角和定理
【解析】【分析】先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由∠1=20°,∠2=35°求出∠DBC+∠DCB的度数,由三角形内角和定理即可得出结论.
29、【答案】解:在△ABC中,
∵∠A=65°,∠ACB=72°
∴∠ABC=43°
∵∠ABD=30°
∴∠CBD=∠ABC﹣∠ABD=13°
∵CE平分∠ACB
∴∠BCE=
∠ACB=36°
∴在△BCE中,∠BEC=180°﹣13°﹣36°=131°
【考点】三角形内角和定理
【解析】【分析】先根据∠A=65°,∠ACB=72°得出∠ABC的度数,再由∠ABD=30°得出∠CBD的度数,根据CE平分∠ACB得出∠BCE的度数,根据∠BEC=180°﹣∠BCE﹣∠CBD即可得出结论.
六、作图题
30、【答案】解:如图所示,点P即是所求.
【考点】作图—基本作图
【解析】【分析】作两条公路所成角的角平分线,连接村庄AB;作线段AB的垂直平分线,两条直线的交点即为点P.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
八年级上册(浙教版)数学第一单元检测试卷
数学考试
姓名:__________
班级:__________考号:__________
题号
一
二
三
四
五
六
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前
xx
分钟收取答题卡
第Ⅰ卷
客观题
第Ⅰ卷的注释
一、单选题(共10题;共20分)
1、如图,已知在
中,
,
,
,点
是
的重心,则点
到
所在直线的距离等于(
)
A、
B、
C、
D、
2、如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是(
)
A、B、C、D、
3、如图,等腰三角形ABC中,AB=AC,BD是AC边上的高,若∠A=36°,则∠DBC的大小是(
)
A、18°
B、36°
C、54°
D、72°
4、如图,
,垂足为D,
,下列说法正确的是(
)
A、射线AC是
的角平分线
B、直线BD是
的边AD上的高
C、线段AC是
的中线
D、线段AD是
的边BC上的高
5、下列命题中,为真命题的是(
)
A、如果-2x>-2,那么x>1
B、如果a2=b2,那么a3=b3
C、面积相等的三角形全等
D、如果a∥b,b∥c,那么a∥c
6、下列命题中,错误的是(
).
A、平行四边形的对角线互相平分
B、菱形的对角线互相垂直平分
C、矩形的对角线相等且互相垂直平分
D、角平分线上的点到角两边的距离相等
7、如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数(
)
A、1对
B、2对
C、3对
D、4对
8、如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于(
)
A、2
B、
C、
D、
9、如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )
A、4
B、6
C、8
D、10
10、在下列命题中,正确的是(
)
A、一组对边平行的四边形是平行四边形
B、有一个角是直角的四边形是矩形
C、有一组邻边相等的平行四边形是菱形
D、对角线互相垂直平分的四边形是正方形
第Ⅱ卷
主观题
第Ⅱ卷的注释
二、填空题(共10题;共10分)
11、如图,BC//EF,AC//DF,添加一个条件________,使得△ABC≌△DEF.
12、如图,a//b,∠1=40°,∠2=80°,则∠3=________度.
13、如图,依据尺规作图的痕迹,计算∠α=________°.
14、如图,△ABC中,∠A=100°,若BM、CM分别是△ABC的外角平分线,则∠M=________.
15、命题“同角的余角相等”改写成“如果…那么…”的形式是________.
16、如图,
,
,则
=________°.
17、如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件________,使△ABC≌△DBE(只需添加一个即可,不添加辅助线).
18、如图,ΔABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到ΔA′B′C′,且点A在A′B′上,则旋转角为________.
19、已知,△ABC,按如下步骤作图:
⑴以A为圆心,AC长为半径画弧;
⑵以B为圆心,BC长为半径画弧,与前一条弧相交于点D,
⑶连接CD.
若AC=6,CD=8,则sin∠CAB=________.
20、命题“内错角相等,两直线平行”的逆命题是________.这逆命题是________命题(填“真或假”)
三、综合题(共2题;共20分)
21、如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
22、已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9;
(1)求AC的长
(2)求四边形ABCD的面积
四、解答题(共2题;共20分)
23、如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么?
24、如图,在△ABC中,AB
=AC,BD⊥AC,CE⊥AB,求证:BD=CE.
五、计算题(共5题;共25分)
25、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.
26、如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠B=24°,∠C=44°.求:∠DAE的度数.
27、已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,求∠B的度数.
28、如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
29、如图,∠A=65°,∠ABD=30°,∠ACB=72°,且CE平分∠ACB,求∠BEC的度数.
六、作图题(共1题;共5分)
30、作图题(尺规作图,不写作法,保留作图痕迹)
“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图),准备建立一个燃气中心站P
,
使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.
答案解析部分
一、单选题
1、【答案】A
【考点】全等三角形的判定与性质,相似三角形的判定与性质,等腰直角三角形
【解析】【解答】解:如图,连接CP并延长交AB于D,连接BP交AC于E,并延长到F,使EF=PE,
∵∠C=90°,AC=BC,AB=6,
∴AC=BC=3,
又∵P为△ABC的重心,
∴CD=AB=3.∠CDB=90°
在△AEF和△CEP中,
∵
∴△AEF≌△CEP.
∴∠FAD=90°,CP=AF=3-DP.
又∵CD‖FA,
∴△BPD∽△BFA.
∴=.
∴=.
∴PD=1.
故答案为A.
【分
析】如图,根据三角形的重心是三条中线的交点,根据等腰直角三角形可知CD=3,可连接CP并延长交AB于D,则∠FAD=90°,连接BP交AC于E,
并延长到F,使EF=PE,然后可知△A,可得EF≌△CEP,∠FAD=90°,CP=AF=3-DP,因此可根据两角对应相等的两三角形相似,可得
△BPD∽△BFA.即可求出PD.
2、【答案】A
【考点】三角形三边关系,正方形的性质
【解析】【解答】解:选项A不正确.理由正方形的边长为10,所以对角线=10
≈14,
因为15>14,所以这个图形不可能存在.
故选A.
【分析】利用勾股定理求出正方形的对角线为10
≈14,由此即可判定A不正确.
3、【答案】A
【考点】三角形内角和定理,等腰三角形的性质
【解析】【解答】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°
∵BD是AC边上的高,
∴BD⊥AC,
∴∠ADB=90°,
∴∠DBC=90°-72°=18°.
故选A.
4、【答案】D
【考点】三角形的角平分线、中线和高
【解析】【解答】解:三角形的角平分线、高线均为线段,故A、B错误;
线段AC是
的角平分线,故C错误;
由
可知,线段AD是
的边BC上的高,故D正确.
故选D.
5、【答案】D
【考点】命题与定理
【解析】【解答】解:A项如果-2x>-2,那么x<1,故为假命题;
B项当a与b的符号不同时,a2=b2时,a2≠b2
,
故为假命题;
C项由于“面积相等的三角形全等”的逆否命题“不全等的三角形面积不相等”显然为假,故为假命题.
D项平行于同一直线的两条直线平行,故为真命题,
故选D.
【分析】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫假命题.
判断命题的真假关键是要熟悉课本中的性质定理.
6、【答案】C
【考点】角平分线的性质,平行四边形的性质,菱形的性质,矩形的性质,命题与定理
【解析】【解答】解:A.根据平行四边形的性质可得,平行四边形的对角线互相平分,故A正确;
B.根据菱形的性质可得,菱形的对角线互相垂直平分,故B正确;
C.根据矩形的性质可得,矩形的对角线相等且互相平分,而不一定垂直,故C错误;
D.根据角平分线的性质可得,角平分线上的点到角的两边距离相等,故D正确
故选:C.
7、【答案】D
【考点】全等三角形的判定,平行四边形的性质
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).
8、【答案】C
【考点】线段垂直平分线的性质,勾股定理,作图—基本作图
【解析】【解答】解:在Rt△ACB中,由勾股定理得:BC=
=4,
连接AE,
从作法可知:DE是AB的垂直平分线,
根据性质得出AE=BE,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2
,
即32+(4﹣AE)2=AE2
,
解得:AE=
,
在Rt△ADE中,AD=
AB=
,由勾股定理得:DE2+(
)2=(
)2
,
解得:DE=
.
故选C.
【分析】根据勾股定理求出BC,根据线段垂直平分线性质求出AE=BE,根据勾股定理求出AE,再根据勾股定理求出DE即可.
9、【答案】C
【考点】等腰三角形的判定与性质,勾股定理,平行四边形的性质,作图—基本作图
【解析】【解答】解:连结EF,AE与BF交于点O,如图,
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=
BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=
=
=4,
∴AE=2AO=8.
故选C.
【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=
BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
10、【答案】C
【考点】命题与定理
【解析】【解答】解:A、应为两组对边平行的四边形是平行四边形;
B、有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;
C、符合菱形定义;
D、应为对角线互相垂直平分且相等的四边形是正方形.
故选:C.
【分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.两组对边平行的四边形是平行四边形;有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;有一组邻边相等的平行四边形是菱形;对角线互相垂直平分且相等的四边形是正方形.
二、填空题
11、【答案】AB=DE或BC=EF或AC=DF
【考点】全等三角形的判定
【解析】【解答】解:∵BC//EF,
∴∠ABC=∠E,
∵AC//DF,
∴∠A=∠EDF,
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF,
同理,BC=EF或AC=DF也可求证△ABC≌△DEF.
故答案为AB=DE或BC=EF或AC=DF均可.
【分析】本题要判定△ABC≌△DEF,易证∠A=∠EDF,∠ABC=∠E,故添加AB=DE、BC=EF或AC=DF根据ASA、AAS即可解题.
12、【答案】120
【考点】平行线的性质,三角形的外角性质
【解析】【解答】解:如图,∵a//b,∠2=80°,
∴∠4=∠2=80°(两直线平行,同位角相等)
∴∠3=∠1+∠4=40°+80°=120°.
故答案为120°.
【分析】先根据两直线平行,同位角相等,求出∠2的同位角的度数,再利用三角形的外角的性质求得∠3的度数.
13、【答案】56
【考点】作图—基本作图
【解析】【解答】解:∵四边形ABCD的矩形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=
∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°﹣34°=56°,
∴∠α=56°.
故答案为:56.
【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.
14、【答案】40°
【考点】角平分线的定义,三角形内角和定理,三角形的外角性质
【解析】【解答】解:∵∠A=100°,
∴∠ABC+∠ACB=180° ∠A=80°,
∴∠DBC+∠ECB=180° ∠ABC+180° ∠ACB=360° (∠ABC+∠ACB)=360° 80°=280°,
∵BM、CM分别平分∠DBC和∠ECB,
∴∠MBC+∠MCB=
(∠DBC+∠ECB)=
×280°=140°,
∴∠M=180° (∠OBC+∠OCB)=180° 140°=40°,
故答案为:40°.
15、【答案】如果两个角是同一个角的余角,那么这两个角相等.
【考点】命题与定理
【解析】【解答】解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
16、【答案】
【考点】三角形的外角性质
【解析】【解答】解:连接AC并延长,标注点E,
∵∠DCE=∠D+∠DAC,
∠BCE=∠B+∠BAC,
∠BCE+∠DCE=106°,∠A=∠B=47°,
∴∠BCE+∠DCE=∠D+∠DAB+∠B=106°,
∴∠D=106°-47°-47°=12°.
故答案为:12.
【分析】利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.
17、【答案】∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可).
【考点】全等三角形的判定
【解析】【解答】解:∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠ABC=∠DBE,
∵AB=DB,
∴①用“角边角”,需添加∠BDE=∠BAC,
②用“边角边”,需添加BE=BC,
③用“角角边”,需添加∠ACB=∠DEB.
18、【答案】50°
【考点】三角形内角和定理,全等三角形的性质,旋转的性质
【解析】【解答】解:∵将△ACB绕点C顺时针旋转得到
,
∴△ACB≌
,
∴∠A′=∠BAC,AC=CA′,
∴∠A′=∠CAA′,
∴∠CAA′=∠BAC.
∵△ACB中,∠ACB=90°,∠ABC=25°,
∴∠BAC=90 ∠ABC=65°,
∴∠BAC=∠CAA′=65°,
∴∠B′AB=180° 65° 65°=50°,
∴∠ACB′=180° 25° 50° 65°=40°,
∴∠B′CB=90° 40°=50°.
故答案为:50°.
19、【答案】
【考点】作图—基本作图,解直角三角形
【解析】【解答】解:如图,连接AD、BD.AB与CD交于点O.
∵AC=AD,BC=BD,
∴AB垂直平分线段CD,
∴CO=OD=4,
在Rt△AOC中,∵∠AOC=90°,AC=6,CO=4,
∴sin∠ACB=
=
=
.
故答案为
.
【分析】如图,连接AD、BD.AB与CD交于点O.首先证明AB垂直平分线段CD,根据sin∠ACB=
,即可解决问题.
20、【答案】两直线平行,内错角相等;真
【考点】命题与定理
【解析】【解答】解:“内错角相等,两直线平行”的逆命题是“两直线平行,内错角相等”,
它是真命题,
故答案为:两直线平行,内错角相等;真.
【分析】写出原命题的逆命题,根据平行线的性质判断即可.
三、综合题
21、【答案】(1)解:如图,DE为所作;
(2)证明:如图,
∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=30°,
即BD平分∠ABC,
而DE⊥AB,DC⊥BC,
∴DE=DC.
【考点】线段垂直平分线的性质,含30度角的直角三角形,作图—基本作图
【解析】【分析】(1)利用基本作图(作已知线段的垂直平分线)作DE垂直平分AB;(2)先利用线段垂直平分线的性质得到DA=DB,则∠DBA=∠A=30°,再证明BD平分∠ABC,然后根据角平分线的性质定理可得到结论.
22、【答案】(1)解:∵∠ACB=90°
∴AC2=AB2-BC2=172-82=225
∴AC=15
(2)解:∵AD2+CD2=92+122=225=AC2
∴∠D=90°
∴S四边形ABCD=
S△ABC+
S△ACD=
8×15÷2+12×9÷2=114.
【考点】三角形的面积,勾股定理,勾股定理的逆定理
【解析】【分析】(1)根据勾股定理可求AC的长;
(2)根据勾股定理的逆定理可判断∠D=90°,四边形ABCD的面积=△ABC的面积+△ADC的面积.
四、解答题
23、【答案】解:相等;
证明:在△ABC和△ADC中
∴△ABC≌△ADC(ASA),
∴BC=DC,
在△BEC和△DEC中
,
∴△BEC≌△DEC(SAS),
∴BE=DE
【考点】全等三角形的判定与性质
【解析】【分析】先证△ABC≌△ADC(ASA),再证△BEC≌△DEC(SAS),根据全等三角形的对应边相等可以得到BE=DE.
24、【答案】证明:∵BD⊥AC,CE⊥AB.
∴∠ADB=∠AEC=90°.
在△ABD和△ACE中.
∴△ABD≌△AEC(AAS)
∴BD=CE.
【考点】全等三角形的判定与性质
【解析】【分析】根据BD⊥AC,CE⊥AB,得出∠ADB=∠AEC=90°.再根据三角形全等的判定ASA得出△ABD≌△AEC;再根据全等三角形的性质得出BD=CE.
五、计算题
25、【答案】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=6,
∴DB=AB﹣AD=6﹣4=2
【考点】平行线的性质,全等三角形的判定与性质
【解析】【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=6,FC=4,即可求线段DB的长.
26、【答案】解:∵△ABC中,∠B=24°,∠C=44°
∴∠BAC=180°﹣∠B﹣∠C=112°,
∵AE是∠BAC的平分线,
∴∠EAC=
∠BAC=56°,
∵AD是BC边上的高,
∴在直角△ADC中,∠DAC=90°﹣∠C=90°﹣44°=46°,
∴∠DAE=∠EAC﹣∠DAC=56°﹣46°=10°.
【考点】三角形的角平分线、中线和高,三角形内角和定理
【解析】【分析】根据三角形的内角和定理,可求得∠BAC的度数,由AE是∠BAC的平分线,可得∠EAC的度数,在直角△ADC中,可求出∠DAC的度数,根据∠DAE=∠EAC﹣∠DAC,即可得出结论.
27、【答案】解:∵∠A=30°,
∴∠B+∠C=180°﹣∠A=150°,
∵∠C=2∠B,
∴3∠B=150°,
∴∠B=50°.
【考点】三角形内角和定理
【解析】【分析】根据三角形内角和定理求出∠B+∠C的度数,把∠C=2∠B代入求出即可.
28、【答案】解:∵在△ABC中,∠A=62°,
∴∠ABC+∠ACB=180°﹣62°=118°.
∵∠1=20°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=118°﹣20°﹣35°=63°.
∴∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣63°=117°.
【考点】三角形内角和定理
【解析】【分析】先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由∠1=20°,∠2=35°求出∠DBC+∠DCB的度数,由三角形内角和定理即可得出结论.
29、【答案】解:在△ABC中,
∵∠A=65°,∠ACB=72°
∴∠ABC=43°
∵∠ABD=30°
∴∠CBD=∠ABC﹣∠ABD=13°
∵CE平分∠ACB
∴∠BCE=
∠ACB=36°
∴在△BCE中,∠BEC=180°﹣13°﹣36°=131°
【考点】三角形内角和定理
【解析】【分析】先根据∠A=65°,∠ACB=72°得出∠ABC的度数,再由∠ABD=30°得出∠CBD的度数,根据CE平分∠ACB得出∠BCE的度数,根据∠BEC=180°﹣∠BCE﹣∠CBD即可得出结论.
六、作图题
30、【答案】解:如图所示,点P即是所求.
【考点】作图—基本作图
【解析】【分析】作两条公路所成角的角平分线,连接村庄AB;作线段AB的垂直平分线,两条直线的交点即为点P.
(
1
)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
