第2章 简单事件的概率检测试卷(含答案)
文档属性
| 名称 | 第2章 简单事件的概率检测试卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-10 00:00:00 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册数学(浙教版)第二单元检测试卷
数学考试
姓名:__________
班级:__________考号:__________
题号
一
二
三
四
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前
xx
分钟收取答题卡
第Ⅰ卷
客观题
第Ⅰ卷的注释
一、单选题(共10题;共20分)
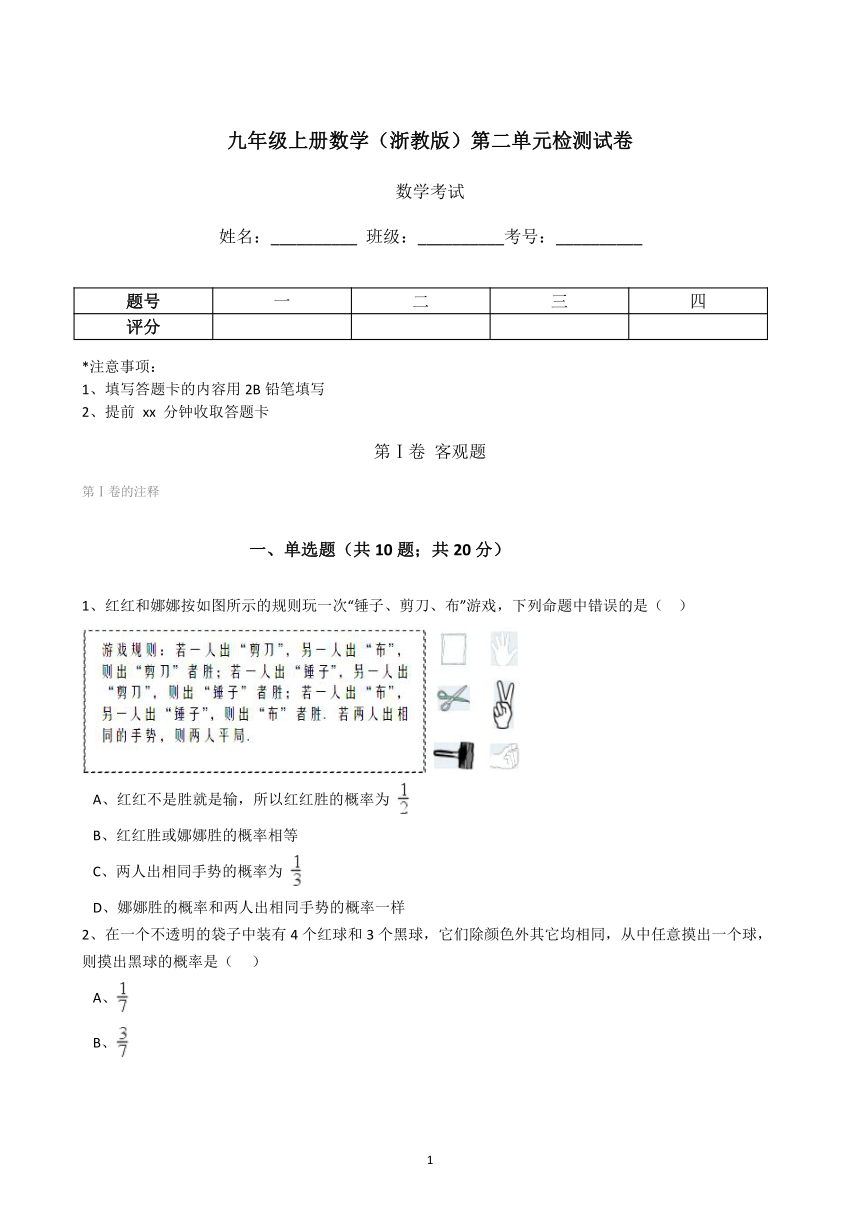
1、红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是(
)
A、红红不是胜就是输,所以红红胜的概率为
B、红红胜或娜娜胜的概率相等
C、两人出相同手势的概率为
D、娜娜胜的概率和两人出相同手势的概率一样
2、在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是(
)
A、
B、
C、
D、
3、下列图形:
任取一个是中心对称图形的概率是(
)
A、
B、
C、
D、1
4、下列说法正确的是(
)
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机会相同.
A、①②
B、②③
C、③④
D、①③
5、盒子中有白色乒乓球8个和黄色乒乓球若干个,为求得盒中黄色乒乓球的个数,某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色,如此重复360次,摸出白色乒乓球90次,则黄色乒乓球的个数估计为(
)
A、90个
B、24个
C、70个
D、32个
6、袋中放有一套(五枚)北京2008年奥运会吉祥物福娃纪念币,依次取出(不放回)两枚纪念币,恰好能够组成“欢迎”的概率是
(
)
A、
B、
C、
D、
7、一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是(
)
A、至少有1个球是红球
B、至少有1个球是白球
C、至少有2个球是红球
D、至少有2个球是白球
8、“I
am
a
good
student.”这句话中,字母”a“出现的频率是
(
)
A、2
B、
C、
D、
9、一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为(
)
A、
B、
C、
D、
10、有20张背面完全一样的卡片,其中8张正面印有天鹅湖风光,7张正面印有黄河入海口自然风景,5张正面印有孙武湖景色.把这些卡片的背面朝上,搅匀后从中随机抽出一张卡片,抽到正面是天鹅湖风光卡片的概率是(
)
A、
B、
C、
D、
第Ⅱ卷
主观题
第Ⅱ卷的注释
二、填空题(共10题;共20分)
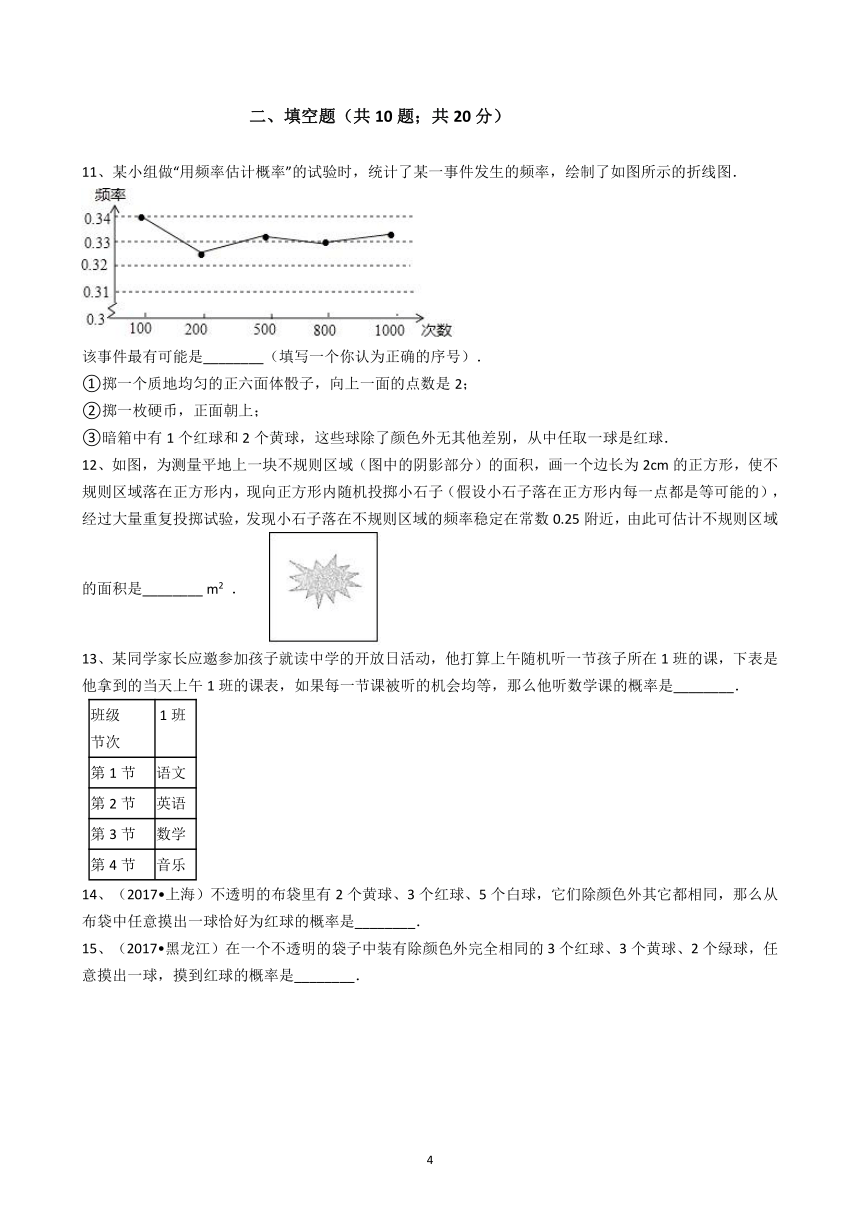
11、某小组做“用频率估计概率”的试验时,统计了某一事件发生的频率,绘制了如图所示的折线图.
该事件最有可能是________(填写一个你认为正确的序号).
①掷一个质地均匀的正六面体骰子,向上一面的点数是2;
②掷一枚硬币,正面朝上;
③暗箱中有1个红球和2个黄球,这些球除了颜色外无其他差别,从中任取一球是红球.
12、如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是________ m2
.
13、某同学家长应邀参加孩子就读中学的开放日活动,他打算上午随机听一节孩子所在1班的课,下表是他拿到的当天上午1班的课表,如果每一节课被听的机会均等,那么他听数学课的概率是________.
班级
节次
1班
第1节
语文
第2节
英语
第3节
数学
第4节
音乐
14、(2017 上海)不透明的布袋里有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是________.
15、(2017 黑龙江)在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球,任意摸出一球,摸到红球的概率是________.
16、如图1,有六张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“成”的概率是________.
17、透明的口袋中有6个红色的小正方体和若干个黄色的小正方体,这些小正方体除颜色外其他都相同.将口袋中的小正方体摇匀,从中一次摸出10个小正方体,求出其中红色小正方体数量与10的比值,再把它放回口袋中,不断重复上述过程,共摸30次,红色小正方体数量与10的比值的平均数为0.3,口袋中大约有________个黄色小正方体.
18、小明正在玩飞镖游戏,如果他将飞镖随意投向如图所示的正方形网格中,那么投中阴影部分的概率是________;
19、对于平面内任意一个凸四边形ABCD,现从以下四个关系式:
①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是________.
20、有5张正面分别标有数字-2,0,2,4,6的不透明卡片,它们除数不同外其余全部相同,先将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为
,则使关于
不等式组
有实数解的概率为________;
三、综合题(共5题;共30分)
21、为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
22、学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是________;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
23、车辆经过润扬大桥收费站时,4个收费通道
A、B、C、D中,可随机选择其中的一个通过.
(1)一辆车经过此收费站时,选择
A通道通过的概率是________;
(2)求两辆车经过此收费站时,选择不同通道通过的概率.
24、编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次,这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
25、(2017 营口)如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
四、解答题(共5题;共30分)
26、小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.
27、小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.
28、小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
29、为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别
睡眠时间x(小时)
A
4.5≤x<5.5
B
5.5≤x<6.5
C
6.5≤x<7.5
D
7.5≤x<8.5
E
8.5≤x<9.5
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
30、如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色.转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明与小颖参与游戏:小明转动甲盘,小颖转动乙盘.
(1)小明转出的颜色为红色的概率为________;
(2)小明转出的颜色为黄色的概率为________;
(3)小颖转出的颜色为黄色的概率为________;
(4)两人均转动转盘,如果转出的颜色为红,则胜出.你认为该游戏公平吗?为什么?
答案解析部分
一、单选题
1、【答案】A
【考点】概率的意义,概率公式
【解析】【解答】解:如下树状图,
一共有9种等可能的情况,
其中红红胜的概率是P=,
娜娜胜的概率是P=,
两人出相同手势的概率为P=,
故A错误.
故选A.
【分析】用树状图列出所有等可能的情况是9种,再找出红红胜的情况,娜娜胜的情况,分别求出她们获胜的概率,再比较.
2、【答案】B
【考点】概率的意义,利用频率估计概率
【解析】【解答】解:摸出一个球一共有3+4=7种同可能的情况,
而抽出一个是黑球的有3种情况,
故P(摸出黑球)=
.
故选B.
【分析】用简单的概率公式解答P=
;在这里,n是球的总个数,m是黑球的个数.
3、【答案】C
【考点】概率公式
【解析】【解答】解:∵共有4种等可能的结果,任取一个是中心对称图形的有3种情况,
∴任取一个是中心对称图形的概率是:
.
故选C.
【分析】由共有4种等可能的结果,任取一个是中心对称图形的有3种情况,直接利用概率公式求解即可求得答案.
4、【答案】B
【考点】可能性的大小,概率的意义,利用频率估计概率
【解析】【解答】解:①错误,实验条件会极大影响某事件出现的频率;②正确;③正确;④错误,“两个正面”、“两个反面”的概率为
,“一正一反”的机会较大,为
.
故选B.
【分析】根据频率与概率的关系分析各个选项即可.
5、【答案】B
【考点】利用频率估计概率
【解析】【解答】解:设黄球数为x个,
∵重复360次,摸出白色乒乓球90次
∴白球的概率为
∴
=
解得x=24.
故选B.
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再利用频率等于原白球数除以总球数进行求解.
6、【答案】C
【考点】概率公式
【解析】【解答】解:根据题意可知,第一次可以取出5种情况,第二次可以取出4种情况,共有5×4=20种可能,恰好能够组成“欢迎”的有2种,所以概率是
,
故选C.
7、【答案】B
【考点】随机事件,可能性的大小
【解析】【解答】解:A.
至少有1个球是红球是随机事件,选项错误;
B.
至少有1个球是白球是必然事件,选项正确;
C.
至少有2个球是红球是随机事件,选项错误;
D.
至少有2个球是白球是随机事件,选项错误。
故选B.
8、【答案】B
【考点】概率公式
【解析】【解答】解:这句话中,15个字母a出现了2次,
所以字母“a”出现的频率是
.
故选B.
9、【答案】C
【考点】概率公式
【解析】【解答】解:从中随机摸出一个小球,恰好是红球的概率P=
=
.
故选C.
【分析】直接根据概率公式求解.
10、【答案】C
【考点】概率公式
【解析】【解答】解:共有图片20张,天鹅湖风光卡片8张,抽到正面是天鹅湖风光卡片的概率是:
=
.
故选C.
【分析】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数;二者的比值就是其发生的概率的大小.
二、填空题
11、【答案】③
【考点】频数(率)分布折线图,随机事件,利用频率估计概率
【解析】【解答】解:由折线统计图知,随着试验次数的增加,频率逐渐稳定在0.33,即
左右,
①中向上一面的点数是2的概率为
,不符合题意;
②中掷一枚硬币,正面朝上的概率为
,不符合题意;
③中从中任取一球是红球的概率为
,符合题意,
故答案为:③.
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈
,计算三个选项的概率,约为
者即为正确答案.
12、【答案】1
【考点】利用频率估计概率
【解析】【解答】解:∵经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,
∴小石子落在不规则区域的概率为0.25,
∵正方形的边长为2cm,
∴面积为4cm2
,
设不规则部分的面积为s,
则
=0.25,
解得:s=1,
故答案为:1.
【分析】首先确定小石子落在不规则区域的概率,然后利用概率公式求得其面积即可.
13、【答案】
【考点】概率公式
【解析】【解答】解:由表可知,当天上午1班的课表中听一节课有4种等可能结果,其中听数学课的有1种可能,
∴听数学课的可能性概率是
.
故答案是:
.
【分析】根据概率公式可得答案.
14、【答案】
【考点】概率公式
【解析】【解答】解:∵在不透明的袋中装有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,
∴从这不透明的袋里随机摸出一个球,所摸到的球恰好为红球的概率是:
=
.
故答案为:
.
【分析】由在不透明的袋中装有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,直接利用概率公式求解,即可得到任意摸出一球恰好为红球的概率.
15、【答案】
【考点】概率公式
【解析】【解答】解:∵袋子中共有8个球,其中红球有3个,
∴任意摸出一球,摸到红球的概率是
,
故答案为:
.
【分析】根据随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,用红球的个数除以总个数,求出恰好摸到红球的概率是多少即可.
16、【答案】
【考点】概率公式
【解析】【解答】解:从中任意翻开一张是汉字“成”的概率是
=
,
故答案为:
.
【分析】共有6个字,其中“成”字有3个,故概率为
=
.
17、【答案】14
【考点】利用频率估计概率
【解析】【解答】解:因为将口袋中的小正方体摇匀,从中一次摸出10个小正方体,求出其中红色小正方体数量与10的比值,再把它放回口袋中,不断重复上述过程,共摸30次,红色小正方体数量与10的比值的平均数为0.3,
所以摸到红色小正方体的概率为0.3,
所以可估计这个口袋中小正方体的总数量为6÷0.3=20(个),
则这个口袋中黄色小正方体的数量=20﹣6=14(个).
故答案为14.
【分析】先利用频率估计概率得到摸到红色小正方体的概率为0.3,然后根据概率公式可估计这个口袋中小正方体的总数量,再计算黄色小正方体的数量.
18、【答案】
【考点】概率公式
【解析】【解答】解:观察这个图可知:阴影部分占6个小正方形,占总数16个的
=
,故其概率是
.
故答案为:
.
【分析】
19、【答案】
【考点】概率公式
【解析】【解答】解:从四个条件中选两个共有六种可能:①②、①③、①④、②③、②④、③④,
其中只有①②、①③和③④可以判断四边形ABCD是平行四边形,
所以能够得出这个四边形ABCD是平行四边形的概率是
.
【分析】概率=所求情况数与总情况数之比;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;一组对边平行,一组对角相等的四边形是平行四边形.
20、【答案】
【考点】概率公式
【解析】【解答】首先确定不等式的解,然后根据有确定a的取值范围,再利用概率公式求解即可.
解:解关于x不等式
得
,
∵关于x不等式
有实数解,
∴
解得a<1.
∴使关于x不等式
有实数解的概率为
.
故答案为:
【分析】本题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,期中事件A出现m种结果,那么事件A的概率P(A)=
.
三、综合题
21、【答案】(1)甲投放的垃圾恰好是A类的概率为:
;
(2)解:如图所示:
,
由图可知,共有18种可能结果,其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果有12种,
所以,P(乙投放的垃圾恰有一袋与甲投放的垃圾是同类)=
=
;
即,乙投放的垃圾恰有一袋与甲投放的垃圾是同一类的概率是:
.
【考点】列表法与树状图法,概率公式
【解析】【解答】解:∵垃圾要按A,B,C三类分别装袋,甲投放了一袋垃圾,
【分析】(1)直接利用概率公式求出甲投放的垃圾恰好是A类的概率;(2)首先利用树状图法列举出所有可能,进而利用概率公式求出答案.
22、【答案】(1)
(2)解:画树状图如下:
由树状图可知,一共有16种等可能结果,其中恰好取到两个白粽子有4种结果,
∴小明恰好取到两个白粽子的概率为
=
【考点】列表法与树状图法,概率公式
【解析】【解答】解:(1)∵甲盘中一共有4个粽子,其中豆沙粽子只有1个,
∴小明从甲盘中任取一个粽子,取到豆沙粽的概率是
,
故答案为:
;
【分析】(1)由甲盘中一共有4个粽子,其中豆沙粽子只有1个,根据概率公式求解可得;(2)根据题意画出树状图,由树状图得出一共有16种等可能结果,其中恰好取到两个白粽子有4种结果,根据概率公式求解可得.
23、【答案】(1)
(2)解:设两辆车为甲,乙,
如图,两辆车经过此收费站时,会有16种可能的结果,其中选择不同通道通过的有12种结果,
∴选择不同通道通过的概率=
=
.
【考点】列表法与树状图法,概率公式
【解析】【解答】解:(1)选择
A通道通过的概率=
,
故答案为:
,
【分析】(1)根据概率公式即可得到结论;(2)画出树状图即可得到结论.
24、【答案】(1)解:第6名学生命中的个数为5×40%=2,
则第6号学生的积分为2分,
补全条形统计图如下:
(2)解:这6名学生中,命中次数多于5×50%=2.5次的有2、3、4、5号这4名学生,
∴选上命中率高于50%的学生的概率为
=
(3)解:由于前6名学生积分的众数为3分,
∴第7号学生的积分为3分
【考点】条形统计图,中位数、众数,概率公式
【解析】【分析】(1)由第6名学生命中的个数为5×40%=2可得答案,并补全条形图;(2)由这6名学生中,命中次数多于5×50%=2.5次的有2、3、4、5号这4名学生,根据概率公式可得;(3)根据众数的定义得出前6名学生积分的众数即可得.
25、【答案】(1)解:共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是
;
(2)解:列表得:
A
B
C
D
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
共产生12种结果,每种结果出现的可能性相同,其中两张牌都是轴对称图形的有6种,
∴P(两张都是轴对称图形)=
,因此这个游戏公平.
【考点】轴对称图形,列表法与树状图法,游戏公平性,中心对称及中心对称图形,概率公式
【解析】【分析】(1)首先根据题意结合概率公式可得答案;(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
四、解答题
26、【答案】解:不公平,
画树状图得:
∵共有9种等可能的结果,数字的差为偶数的有4种情况,
∴P(小华胜)=
,P(小军胜)=
,
∵
≠
,
∴这个游戏对双方不公平.
【考点】列表法与树状图法,游戏公平性
【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与数字的差为偶数的情况,再利用概率公式求解即可求得答案.
27、【答案】解:这个游戏对双方是公平的.
列表得:
∴一共有6种情况,积大于2的有3种,
∴P(积大于2)=
=
,
∴这个游戏对双方是公平的.
【考点】游戏公平性
【解析】【分析】首先依据题先用列表法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
28、【答案】解:这个游戏对双方是公平的.
如图,
∴一共有6种情况,和大于4的有3种,
∴P(和大于4)=
=
,
∴这个游戏对双方是公平的
【考点】列表法与树状图法,游戏公平性
【解析】【分析】首先依据题先用树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
29、【答案】(Ⅰ)a=1﹣10%﹣25%﹣35%﹣25%=5%,
即统计图中a的值是5%;
(Ⅱ)解:八年级抽到的学生为睡眠严重不足的可能性为:
=
,
九年级抽到的学生为睡眠严重不足的可能性为:5%+25%=30%=0.3
【考点】频数(率)分布表,扇形统计图,条形统计图,可能性的大小
【解析】【分析】(1)根据扇形统计图可以求得a的值;(2)根据统计图中的数据可以求得该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性;
30、【答案】(1)
(2)
(3)
(4)不公平,∵小明转出的颜色为红色的概率为
,小颖转出的颜色为红色的概率为
,而
>
,∴不公平.
【考点】概率的意义,概率公式
【解析】【解答】解:(1)甲盘中一共有6块等面积的颜色块,红色的只有1块,∴P(转出的颜色为红色)=
;
⑵甲盘中一共有6块等面积的颜色块,黄色的有3块,∴P(转出的颜色为黄色)=
;
⑶乙盘中一共有4块等面积的颜色块,黄色的有2块,∴P(转出的颜色为黄色)=
;
故答案为(1)
;(2)
;(3)
.
【分析】运用概率公式P=
计算:(1)和(2)中甲盘中有6块等面积的,红色的有1块,黄色的有3块,即可分别求出概率;(3)乙盘中有4块等面积的,黄色的有2块,即可求出概率;(4)分别求出在甲盘和乙盘中转到红色的概率,比较概率的大小即可得到.
(
1
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
九年级上册数学(浙教版)第二单元检测试卷
数学考试
姓名:__________
班级:__________考号:__________
题号
一
二
三
四
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前
xx
分钟收取答题卡
第Ⅰ卷
客观题
第Ⅰ卷的注释
一、单选题(共10题;共20分)
1、红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是(
)
A、红红不是胜就是输,所以红红胜的概率为
B、红红胜或娜娜胜的概率相等
C、两人出相同手势的概率为
D、娜娜胜的概率和两人出相同手势的概率一样
2、在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是(
)
A、
B、
C、
D、
3、下列图形:
任取一个是中心对称图形的概率是(
)
A、
B、
C、
D、1
4、下列说法正确的是(
)
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机会相同.
A、①②
B、②③
C、③④
D、①③
5、盒子中有白色乒乓球8个和黄色乒乓球若干个,为求得盒中黄色乒乓球的个数,某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色,如此重复360次,摸出白色乒乓球90次,则黄色乒乓球的个数估计为(
)
A、90个
B、24个
C、70个
D、32个
6、袋中放有一套(五枚)北京2008年奥运会吉祥物福娃纪念币,依次取出(不放回)两枚纪念币,恰好能够组成“欢迎”的概率是
(
)
A、
B、
C、
D、
7、一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是(
)
A、至少有1个球是红球
B、至少有1个球是白球
C、至少有2个球是红球
D、至少有2个球是白球
8、“I
am
a
good
student.”这句话中,字母”a“出现的频率是
(
)
A、2
B、
C、
D、
9、一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为(
)
A、
B、
C、
D、
10、有20张背面完全一样的卡片,其中8张正面印有天鹅湖风光,7张正面印有黄河入海口自然风景,5张正面印有孙武湖景色.把这些卡片的背面朝上,搅匀后从中随机抽出一张卡片,抽到正面是天鹅湖风光卡片的概率是(
)
A、
B、
C、
D、
第Ⅱ卷
主观题
第Ⅱ卷的注释
二、填空题(共10题;共20分)
11、某小组做“用频率估计概率”的试验时,统计了某一事件发生的频率,绘制了如图所示的折线图.
该事件最有可能是________(填写一个你认为正确的序号).
①掷一个质地均匀的正六面体骰子,向上一面的点数是2;
②掷一枚硬币,正面朝上;
③暗箱中有1个红球和2个黄球,这些球除了颜色外无其他差别,从中任取一球是红球.
12、如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是________ m2
.
13、某同学家长应邀参加孩子就读中学的开放日活动,他打算上午随机听一节孩子所在1班的课,下表是他拿到的当天上午1班的课表,如果每一节课被听的机会均等,那么他听数学课的概率是________.
班级
节次
1班
第1节
语文
第2节
英语
第3节
数学
第4节
音乐
14、(2017 上海)不透明的布袋里有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是________.
15、(2017 黑龙江)在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球,任意摸出一球,摸到红球的概率是________.
16、如图1,有六张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“成”的概率是________.
17、透明的口袋中有6个红色的小正方体和若干个黄色的小正方体,这些小正方体除颜色外其他都相同.将口袋中的小正方体摇匀,从中一次摸出10个小正方体,求出其中红色小正方体数量与10的比值,再把它放回口袋中,不断重复上述过程,共摸30次,红色小正方体数量与10的比值的平均数为0.3,口袋中大约有________个黄色小正方体.
18、小明正在玩飞镖游戏,如果他将飞镖随意投向如图所示的正方形网格中,那么投中阴影部分的概率是________;
19、对于平面内任意一个凸四边形ABCD,现从以下四个关系式:
①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是________.
20、有5张正面分别标有数字-2,0,2,4,6的不透明卡片,它们除数不同外其余全部相同,先将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为
,则使关于
不等式组
有实数解的概率为________;
三、综合题(共5题;共30分)
21、为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
22、学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是________;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
23、车辆经过润扬大桥收费站时,4个收费通道
A、B、C、D中,可随机选择其中的一个通过.
(1)一辆车经过此收费站时,选择
A通道通过的概率是________;
(2)求两辆车经过此收费站时,选择不同通道通过的概率.
24、编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次,这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
25、(2017 营口)如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
四、解答题(共5题;共30分)
26、小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.
27、小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.
28、小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
29、为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别
睡眠时间x(小时)
A
4.5≤x<5.5
B
5.5≤x<6.5
C
6.5≤x<7.5
D
7.5≤x<8.5
E
8.5≤x<9.5
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
30、如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色.转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明与小颖参与游戏:小明转动甲盘,小颖转动乙盘.
(1)小明转出的颜色为红色的概率为________;
(2)小明转出的颜色为黄色的概率为________;
(3)小颖转出的颜色为黄色的概率为________;
(4)两人均转动转盘,如果转出的颜色为红,则胜出.你认为该游戏公平吗?为什么?
答案解析部分
一、单选题
1、【答案】A
【考点】概率的意义,概率公式
【解析】【解答】解:如下树状图,
一共有9种等可能的情况,
其中红红胜的概率是P=,
娜娜胜的概率是P=,
两人出相同手势的概率为P=,
故A错误.
故选A.
【分析】用树状图列出所有等可能的情况是9种,再找出红红胜的情况,娜娜胜的情况,分别求出她们获胜的概率,再比较.
2、【答案】B
【考点】概率的意义,利用频率估计概率
【解析】【解答】解:摸出一个球一共有3+4=7种同可能的情况,
而抽出一个是黑球的有3种情况,
故P(摸出黑球)=
.
故选B.
【分析】用简单的概率公式解答P=
;在这里,n是球的总个数,m是黑球的个数.
3、【答案】C
【考点】概率公式
【解析】【解答】解:∵共有4种等可能的结果,任取一个是中心对称图形的有3种情况,
∴任取一个是中心对称图形的概率是:
.
故选C.
【分析】由共有4种等可能的结果,任取一个是中心对称图形的有3种情况,直接利用概率公式求解即可求得答案.
4、【答案】B
【考点】可能性的大小,概率的意义,利用频率估计概率
【解析】【解答】解:①错误,实验条件会极大影响某事件出现的频率;②正确;③正确;④错误,“两个正面”、“两个反面”的概率为
,“一正一反”的机会较大,为
.
故选B.
【分析】根据频率与概率的关系分析各个选项即可.
5、【答案】B
【考点】利用频率估计概率
【解析】【解答】解:设黄球数为x个,
∵重复360次,摸出白色乒乓球90次
∴白球的概率为
∴
=
解得x=24.
故选B.
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,先求得白球的频率,再利用频率等于原白球数除以总球数进行求解.
6、【答案】C
【考点】概率公式
【解析】【解答】解:根据题意可知,第一次可以取出5种情况,第二次可以取出4种情况,共有5×4=20种可能,恰好能够组成“欢迎”的有2种,所以概率是
,
故选C.
7、【答案】B
【考点】随机事件,可能性的大小
【解析】【解答】解:A.
至少有1个球是红球是随机事件,选项错误;
B.
至少有1个球是白球是必然事件,选项正确;
C.
至少有2个球是红球是随机事件,选项错误;
D.
至少有2个球是白球是随机事件,选项错误。
故选B.
8、【答案】B
【考点】概率公式
【解析】【解答】解:这句话中,15个字母a出现了2次,
所以字母“a”出现的频率是
.
故选B.
9、【答案】C
【考点】概率公式
【解析】【解答】解:从中随机摸出一个小球,恰好是红球的概率P=
=
.
故选C.
【分析】直接根据概率公式求解.
10、【答案】C
【考点】概率公式
【解析】【解答】解:共有图片20张,天鹅湖风光卡片8张,抽到正面是天鹅湖风光卡片的概率是:
=
.
故选C.
【分析】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数;二者的比值就是其发生的概率的大小.
二、填空题
11、【答案】③
【考点】频数(率)分布折线图,随机事件,利用频率估计概率
【解析】【解答】解:由折线统计图知,随着试验次数的增加,频率逐渐稳定在0.33,即
左右,
①中向上一面的点数是2的概率为
,不符合题意;
②中掷一枚硬币,正面朝上的概率为
,不符合题意;
③中从中任取一球是红球的概率为
,符合题意,
故答案为:③.
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈
,计算三个选项的概率,约为
者即为正确答案.
12、【答案】1
【考点】利用频率估计概率
【解析】【解答】解:∵经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,
∴小石子落在不规则区域的概率为0.25,
∵正方形的边长为2cm,
∴面积为4cm2
,
设不规则部分的面积为s,
则
=0.25,
解得:s=1,
故答案为:1.
【分析】首先确定小石子落在不规则区域的概率,然后利用概率公式求得其面积即可.
13、【答案】
【考点】概率公式
【解析】【解答】解:由表可知,当天上午1班的课表中听一节课有4种等可能结果,其中听数学课的有1种可能,
∴听数学课的可能性概率是
.
故答案是:
.
【分析】根据概率公式可得答案.
14、【答案】
【考点】概率公式
【解析】【解答】解:∵在不透明的袋中装有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,
∴从这不透明的袋里随机摸出一个球,所摸到的球恰好为红球的概率是:
=
.
故答案为:
.
【分析】由在不透明的袋中装有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,直接利用概率公式求解,即可得到任意摸出一球恰好为红球的概率.
15、【答案】
【考点】概率公式
【解析】【解答】解:∵袋子中共有8个球,其中红球有3个,
∴任意摸出一球,摸到红球的概率是
,
故答案为:
.
【分析】根据随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,用红球的个数除以总个数,求出恰好摸到红球的概率是多少即可.
16、【答案】
【考点】概率公式
【解析】【解答】解:从中任意翻开一张是汉字“成”的概率是
=
,
故答案为:
.
【分析】共有6个字,其中“成”字有3个,故概率为
=
.
17、【答案】14
【考点】利用频率估计概率
【解析】【解答】解:因为将口袋中的小正方体摇匀,从中一次摸出10个小正方体,求出其中红色小正方体数量与10的比值,再把它放回口袋中,不断重复上述过程,共摸30次,红色小正方体数量与10的比值的平均数为0.3,
所以摸到红色小正方体的概率为0.3,
所以可估计这个口袋中小正方体的总数量为6÷0.3=20(个),
则这个口袋中黄色小正方体的数量=20﹣6=14(个).
故答案为14.
【分析】先利用频率估计概率得到摸到红色小正方体的概率为0.3,然后根据概率公式可估计这个口袋中小正方体的总数量,再计算黄色小正方体的数量.
18、【答案】
【考点】概率公式
【解析】【解答】解:观察这个图可知:阴影部分占6个小正方形,占总数16个的
=
,故其概率是
.
故答案为:
.
【分析】
19、【答案】
【考点】概率公式
【解析】【解答】解:从四个条件中选两个共有六种可能:①②、①③、①④、②③、②④、③④,
其中只有①②、①③和③④可以判断四边形ABCD是平行四边形,
所以能够得出这个四边形ABCD是平行四边形的概率是
.
【分析】概率=所求情况数与总情况数之比;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;一组对边平行,一组对角相等的四边形是平行四边形.
20、【答案】
【考点】概率公式
【解析】【解答】首先确定不等式的解,然后根据有确定a的取值范围,再利用概率公式求解即可.
解:解关于x不等式
得
,
∵关于x不等式
有实数解,
∴
解得a<1.
∴使关于x不等式
有实数解的概率为
.
故答案为:
【分析】本题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,期中事件A出现m种结果,那么事件A的概率P(A)=
.
三、综合题
21、【答案】(1)甲投放的垃圾恰好是A类的概率为:
;
(2)解:如图所示:
,
由图可知,共有18种可能结果,其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果有12种,
所以,P(乙投放的垃圾恰有一袋与甲投放的垃圾是同类)=
=
;
即,乙投放的垃圾恰有一袋与甲投放的垃圾是同一类的概率是:
.
【考点】列表法与树状图法,概率公式
【解析】【解答】解:∵垃圾要按A,B,C三类分别装袋,甲投放了一袋垃圾,
【分析】(1)直接利用概率公式求出甲投放的垃圾恰好是A类的概率;(2)首先利用树状图法列举出所有可能,进而利用概率公式求出答案.
22、【答案】(1)
(2)解:画树状图如下:
由树状图可知,一共有16种等可能结果,其中恰好取到两个白粽子有4种结果,
∴小明恰好取到两个白粽子的概率为
=
【考点】列表法与树状图法,概率公式
【解析】【解答】解:(1)∵甲盘中一共有4个粽子,其中豆沙粽子只有1个,
∴小明从甲盘中任取一个粽子,取到豆沙粽的概率是
,
故答案为:
;
【分析】(1)由甲盘中一共有4个粽子,其中豆沙粽子只有1个,根据概率公式求解可得;(2)根据题意画出树状图,由树状图得出一共有16种等可能结果,其中恰好取到两个白粽子有4种结果,根据概率公式求解可得.
23、【答案】(1)
(2)解:设两辆车为甲,乙,
如图,两辆车经过此收费站时,会有16种可能的结果,其中选择不同通道通过的有12种结果,
∴选择不同通道通过的概率=
=
.
【考点】列表法与树状图法,概率公式
【解析】【解答】解:(1)选择
A通道通过的概率=
,
故答案为:
,
【分析】(1)根据概率公式即可得到结论;(2)画出树状图即可得到结论.
24、【答案】(1)解:第6名学生命中的个数为5×40%=2,
则第6号学生的积分为2分,
补全条形统计图如下:
(2)解:这6名学生中,命中次数多于5×50%=2.5次的有2、3、4、5号这4名学生,
∴选上命中率高于50%的学生的概率为
=
(3)解:由于前6名学生积分的众数为3分,
∴第7号学生的积分为3分
【考点】条形统计图,中位数、众数,概率公式
【解析】【分析】(1)由第6名学生命中的个数为5×40%=2可得答案,并补全条形图;(2)由这6名学生中,命中次数多于5×50%=2.5次的有2、3、4、5号这4名学生,根据概率公式可得;(3)根据众数的定义得出前6名学生积分的众数即可得.
25、【答案】(1)解:共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是
;
(2)解:列表得:
A
B
C
D
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
共产生12种结果,每种结果出现的可能性相同,其中两张牌都是轴对称图形的有6种,
∴P(两张都是轴对称图形)=
,因此这个游戏公平.
【考点】轴对称图形,列表法与树状图法,游戏公平性,中心对称及中心对称图形,概率公式
【解析】【分析】(1)首先根据题意结合概率公式可得答案;(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
四、解答题
26、【答案】解:不公平,
画树状图得:
∵共有9种等可能的结果,数字的差为偶数的有4种情况,
∴P(小华胜)=
,P(小军胜)=
,
∵
≠
,
∴这个游戏对双方不公平.
【考点】列表法与树状图法,游戏公平性
【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与数字的差为偶数的情况,再利用概率公式求解即可求得答案.
27、【答案】解:这个游戏对双方是公平的.
列表得:
∴一共有6种情况,积大于2的有3种,
∴P(积大于2)=
=
,
∴这个游戏对双方是公平的.
【考点】游戏公平性
【解析】【分析】首先依据题先用列表法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
28、【答案】解:这个游戏对双方是公平的.
如图,
∴一共有6种情况,和大于4的有3种,
∴P(和大于4)=
=
,
∴这个游戏对双方是公平的
【考点】列表法与树状图法,游戏公平性
【解析】【分析】首先依据题先用树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
29、【答案】(Ⅰ)a=1﹣10%﹣25%﹣35%﹣25%=5%,
即统计图中a的值是5%;
(Ⅱ)解:八年级抽到的学生为睡眠严重不足的可能性为:
=
,
九年级抽到的学生为睡眠严重不足的可能性为:5%+25%=30%=0.3
【考点】频数(率)分布表,扇形统计图,条形统计图,可能性的大小
【解析】【分析】(1)根据扇形统计图可以求得a的值;(2)根据统计图中的数据可以求得该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性;
30、【答案】(1)
(2)
(3)
(4)不公平,∵小明转出的颜色为红色的概率为
,小颖转出的颜色为红色的概率为
,而
>
,∴不公平.
【考点】概率的意义,概率公式
【解析】【解答】解:(1)甲盘中一共有6块等面积的颜色块,红色的只有1块,∴P(转出的颜色为红色)=
;
⑵甲盘中一共有6块等面积的颜色块,黄色的有3块,∴P(转出的颜色为黄色)=
;
⑶乙盘中一共有4块等面积的颜色块,黄色的有2块,∴P(转出的颜色为黄色)=
;
故答案为(1)
;(2)
;(3)
.
【分析】运用概率公式P=
计算:(1)和(2)中甲盘中有6块等面积的,红色的有1块,黄色的有3块,即可分别求出概率;(3)乙盘中有4块等面积的,黄色的有2块,即可求出概率;(4)分别求出在甲盘和乙盘中转到红色的概率,比较概率的大小即可得到.
(
1
)
同课章节目录
