2.6直角三角形（2） 练习题

21世纪教育网 –中小学教育资源及组卷应用平台
直角三角形（2）
班级：___________姓名：___________得分：__________
一、选择题
1. 平面上有A、B两个点，以线段AB为一边作等腰直角三角形能作（　　）
A．3个 B．4个 C．6个 D．无数个
2. 如图，在4×3的长方形网格中，已知A、B两点为格点（网格线的交点称为格点），若C也为该网格中的格点，且△ABC为等腰直角三角形，则格点C的个数为（　　）
A．2 B．4 C．6 D．8
3. 用两个完全相同的直角三角板，不能拼成下列图形的是（　　）
A．平行四边形 B．矩形 C．等腰三角形 D．梯形
4. △ABC中，∠A：∠B：∠C=1：2：3，最小边BC=4 cm，最长边AB的长是（　　）
A．5cm B．6cm C．7cm D．8cm
5.如图，将圆桶中的水倒入一个直径为40cm，高为55cm的圆口容器中，圆桶放置的角度与水平线的夹角为45度．若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（　　）
A．10cm B．20cm C．30cm D．35cm
二、填空题
1、将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上，则∠1+∠2=______度．21教育网
2. 在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE交于点P，若∠A=50°，则∠BPC的度数是______度．21cnjy.com
3. 如图，△ABD中，∠BAD=45°，AE⊥BD于E，DF⊥AB于F，交AE于G，BE=4，DE=3，则AG=______．21·cn·jy·com
4. 已知第一个等腰直角三角形的面积为1，以第一个等腰直角三角形的斜边为直角边画第二个等腰直角三角形，又以第二个等腰直角三角形的斜边为直角边画第三个等腰直角三角形，以此类推，第13个等腰直角三角形的面积是______．www.21-cn-jy.com
5. 已知Rt△ABC的两直角边不相等，如果要画一个三角形与Rt△ABC全等，且使所画三角形两条直角边与Rt△ABC的两条直角边分别在同一条直线上（Rt△ABC本身不算），那么满足上述条件的三角形最多能画出______个．2·1·c·n·j·y
三、证明题
1. 已知如图, 在△ABC 中, ∠BAC=2 ∠B,AB=2AC, 求证: △ABC 是直角三角形。
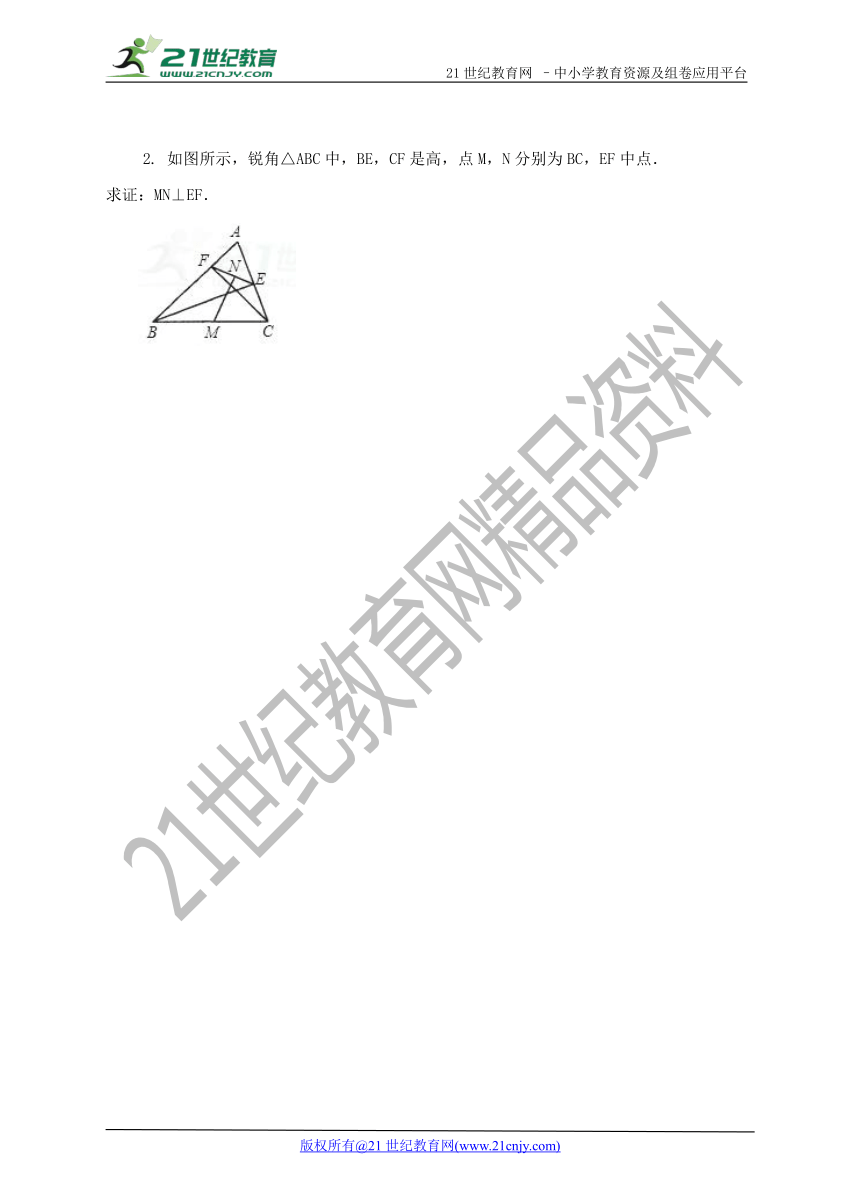
2. 如图所示，锐角△ABC中，BE，CF是高，点M，N分别为BC，EF中点．
求证：MN⊥EF．
参考答案
一、选择题
2、C
【解析】如图所示，，所以有6个
3、D
【解析】如图，把完全重合的含有30°角的两块三角板拼成的图形有三种情况：
分别有等边三角形，等腰三角形，矩形，平行四边形．
4.D
【解析】根据三个内角的比以及三角形的内角和定理，得直角三角形中的最小内角是30°，根据30°所对的直角边是斜边的一半，得最长边是最小边的2倍，即8，故选D．
5.D
【解析】如图，依题意得△ABC是一个斜边为40的等腰直角三角形，
∴此三角形中斜边上的高应该为20，
∴水深至少应为55-20=35cm．
故选D．
二、填空题
1、90
【解析】如图，连接两交点，
根据矩形两边平行，得
∠1+∠2+∠3+∠4=180°，
又矩形的角等于90°，
∴∠3+∠4=90°，
∴∠1+∠2=180°-90°=90°．
故答案为：90．
2、130°
【解析】∵CD，BE分别是AB，AC边上的高，
∴∠BDC=∠AEB=90°
∴∠ABE=90°-50°=40°
∴∠BPC=∠ABE+∠BDP=40+90=130°．
故填130°．
3、7
【解析】由∠BAD=45°，DF⊥AB于F则△ADF是等腰直角三角形，
所以AF=DF，
又∵∠AGF=∠DGE，AE⊥BD于E，
∴∠FAG=∠GDE，
利用等角（或同角）的余角相等可证得∠BAE=∠BDF，
又∵∠AFG=∠DFB=90°，
可证得△AGF≌△DBF（ASA），
所以AG=BD=BE+DE=7．
4. 4096
【解析】根据题意：每作一次图，三角形面积变为原来的2倍；且第一个等腰直角三角形的面积为1，故第13个等腰直角三角形的面积是1×212=4096．21世纪教育网版权所有
5.7
【解析】如图所示：
△AMC，△EFC，△EGC，△HGC，△HFC，△BCN，△MNC共7个，
故答案为：7．
三、证明题
1.【解析】解：过A 作∠CAB 的角平分线, 交BC 于D, 过D 作DE ⊥AB 于E
∵∠BAC=2 ∠B
∴∠CAD= ∠DAB= ∠B
在△DAE 和△DBE 中 ∠DAE= ∠B,
∠DEA= ∠DEB=90 °,DE=DE
∴△DAE ≌△DBE(AAS)
∴AE=BE=AB=AC在△ACD和△AED中AC=AE,
∠CAD=∠EAD,AD=AD
∴△ACD≌△AED(SAS)
∴∠C=∠DEA=90°
∴△ABC为直角三角形
2. 【解析】证明：
连接ME，MF．
则有ME= BC，MF= BC（直角三角形斜边上的中线等于斜边的一半）．
∴ME=MF．
又∵N为EF中点，
∴MN⊥EF．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)