2.4等腰三角形的判定定理 练习题

21世纪教育网 –中小学教育资源及组卷应用平台
等腰三角形的判定定理
班级：___________姓名：___________得分：__________
一、选择题
1、下列能断定△ABC为等腰三角形的是（　　）
A．∠A=30°，∠B=60° B．AB=AC=2，BC=4
C．∠A=50°，∠B=80° D．AB=3、BC=7，周长为13
2. 若三角形的三边a，b，c满足（a-b）（b-c）（c-a）=0，则它一定是（ ）三角形．
A.等边三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形
3. 如图，已知Rt△ABC，∠C=90°，∠A=30°，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有（ ）。21cnjy.com
A.2个　 　B.4个　 　C.6个　 　D.8个
4. 由下列条件可以作出等腰三角形的是（　　）
A．已知等腰三角形的两腰
B．已知一腰和一腰上的高
C．已知底角的度数和顶角的度数
D．已知底边长和底边上的中线的长
5. 如图：有一钢架AOB，∠AOB=10°，为了加固这一钢架，现有长度与OC相等的钢管若干根，焊接在钢架AOB的内部，则最多用去钢管（　　）根．21·cn·jy·com
A．6 B．7 C．8 D．9
二、填空题
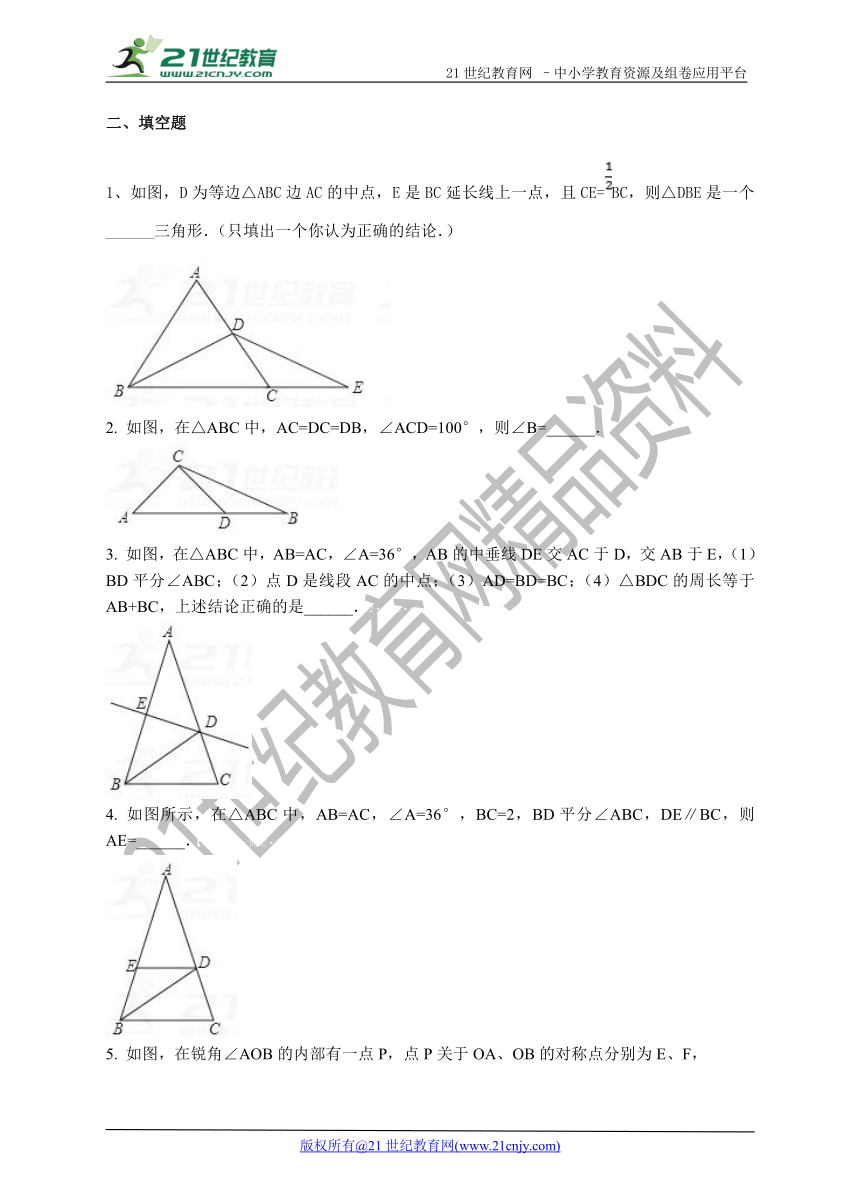
1、如图，D为等边△ABC边AC的中点，E是BC延长线上一点，且CE=BC，则△DBE是一个______三角形．（只填出一个你认为正确的结论．）www.21-cn-jy.com
2. 如图，在△ABC中，AC=DC=DB，∠ACD=100°，则∠B=______．
3. 如图，在△ABC中，AB=AC，∠A=36°，AB的中垂线DE交AC于D，交AB于E，（1）BD平分∠ABC；（2）点D是线段AC的中点；（3）AD=BD=BC；（4）△BDC的周长等于AB+BC，上述结论正确的是______．2·1·c·n·j·y
4. 如图所示，在△ABC中，AB=AC，∠A=36°，BC=2，BD平分∠ABC，DE∥BC，则AE=______．【来源：21·世纪·教育·网】
5. 如图，在锐角∠AOB的内部有一点P，点P关于OA、OB的对称点分别为E、F，
（1）△EOF一定是______三角形；
（2）若∠AOB=45°，则△EOF是______三角形．
三、解答题
1. 如图所示，在△ABC中，∠ABC=60°，∠BAC=75°，AD，CF分别是BC、AB边上的高且相交于点P，∠ABC的平分线BE分别交AD、CF于M、N．21·世纪*教育网
（1）试找出图中所有的等腰三角形，请直接写出来；
（2）若MD=2cm，求DC的长．
2. 上午8时，一条船从海岛A出发，以15海里/时的速度向正北航行，10时到达海岛B处，从A，B望灯塔C，测得∠NAC=43°，∠NBC=86°，问海岛B与灯塔C相距多远？
四、证明题
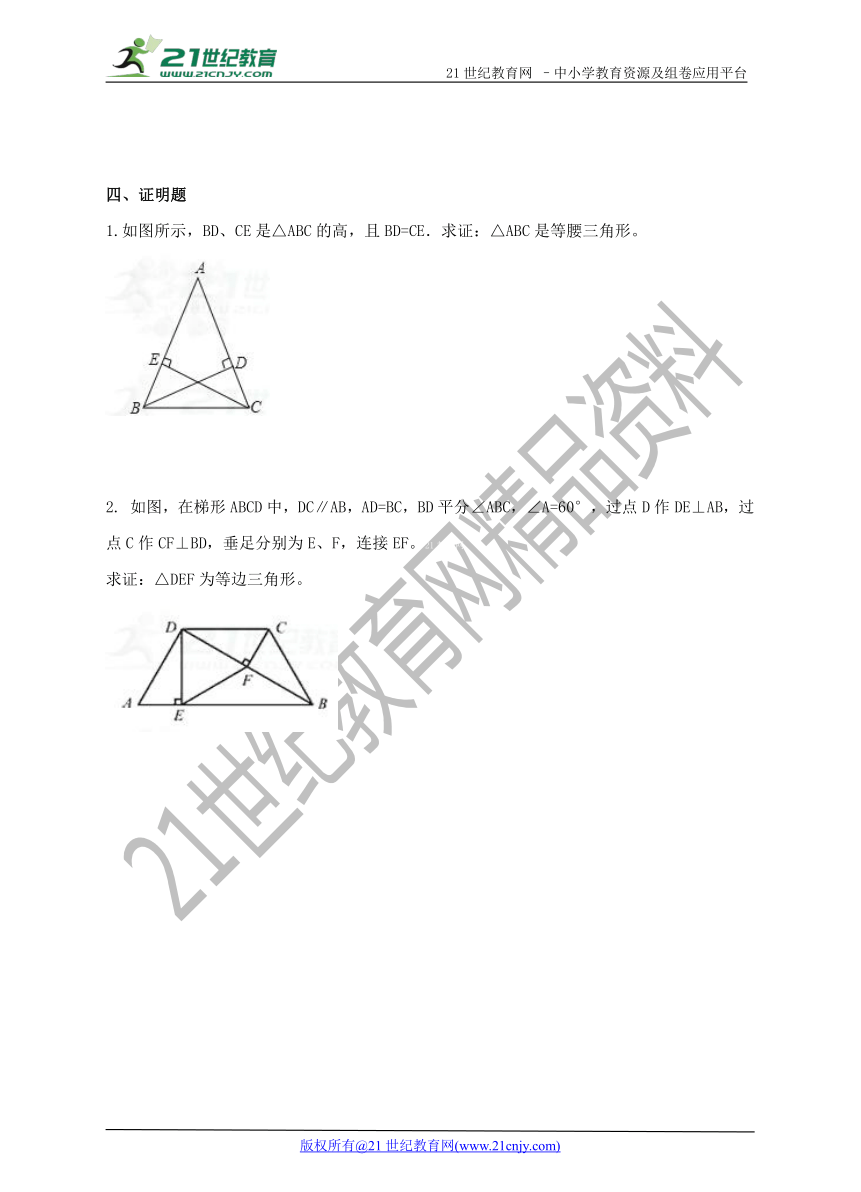
1.如图所示，BD、CE是△ABC的高，且BD=CE．求证：△ABC是等腰三角形。
2. 如图，在梯形ABCD中，DC∥AB，AD=BC，BD平分∠ABC，∠A=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF。21教育网
求证：△DEF为等边三角形。
参考答案
一、选择题
B、∵AB=AC=2，BC=2，
∴2+2=4，
即三条线段不能组成三角形，故本选项错误；
C、∵∠A=50°，∠B=80°，
∴∠C=180°-∠A-∠B=50°，
即∠A=∠C，
∴△ABC是等腰三角形，故本选项正确；
D、∵AB=3，BC=7，周长是13，
∴AC=13-3-7=3，
∵3+3＜7，
∴三条线段不能组成三角形，故本选项错误；
故选C．
2、B
【解析】因为（a-b）（b-c）（c-a）=0，
所以，a=b，b=c，a=c至少有一个成立，
所以，该三角形一定是等腰三角形．
故选B
3、C
【解析】
解：如图，第1个点在AC上，作线段AB的垂直平分线，交AC于点P，则有PA=PB；
第2个点是以A为圆心，以AB长为半径截取AP=AB，交AC延长线上于点P；
第3个点是以A为圆心，以AB长为半径截取AP=AB，在上边于CA延长线上交于点P；
第4个点是以B为圆心，以BA长为半径截取BP=BA，与AC的延长线交于点P；
第5个点是以B为圆心，以BA长为半径截取BP=BA，与BC在左边交于点P；
第6个点是以A为圆心，以AB长为半径截取AP=AB，与BC在右边交于点P；
故符合条件的点P有6个点．
4.D
【解析】已知等腰三角形的两腰，顶角不确定，不能作出等腰三角形，A错误；
已知一腰和一腰上的高，角度不确定，不能作出等腰三角形，B错误；
已知底角的度数和顶角的度数，只知道三个角，不能作出等腰三角形，C错误；
已知底边长和底边上的中线的长可作出等腰三角形，D正确．
故选D
5.C
【解析】∵添加的钢管长度都与OC相等，∠AOB=10°，
∴∠DCE=∠DEC=20°，…从图中我们会发现有好几个等腰三角形，
即第一个等腰三角形的底角是10°，第二个是20°，第三个是30°，四个是40°，五个是50°，六个是60°，七个是70°，八个是80°，九个是90°就不存在了．
所以一共有8个．
故选C．
二、填空题
1、
【解析】∵D为等边△ABC边AC的中点，
∴∠DBC=30°，∠ACB=60°，
∵CE=BC，
∴DC=CE，
∵∠ACB=∠E+∠CDE，
∴∠E=∠CDE=30°，
∴△DBE是一个等腰三角形．
故答案为等腰三角形．
2、20°
【解析】∵AC=DC=DB，∠ACD=100°，
∴∠CAD=（180°-100°）÷2=40°，
∵∠CDB是△ACD的外角，
∴∠CDB=∠A+∠ACD=100°=40°+100°=140°，
∵DC=DB，
∴∠B=（180°-140°）÷2=20°．
故答案为：20°．
3、（1），（3），（4）
【解析】∵△ABC为等腰三角形，DE是AB边的中垂线，所以（1）正确；
∵∠A=36°，
∴∠C=∠BDC=∠ABC=72°，∠ABD=∠A=36°，
∴BC=BD=AD，（3）正确；
△BCD的周长为BC+BD+CD，∵AD=BD，
∴△BCD的周长为AB+BC，（4）正确；
（2）中点D无法判断其是AC的中点，（2）错误
所以正确的结论为（1），（3），（4）．
故填（1），（3），（4）．
4.2
【解析】∵在△ABC中，AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=36°，
∴∠ABD=∠A，
∴BD=AD，
∵DE∥BC，
∴∠AED=∠ADE=∠ABC=∠C=72°，
∴AE=AD，
∴AE=BD，
∵∠BDC=180°-∠DBC-∠C=72°=∠C，
∴BD=BC=2，
∴AE=2．
故答案为：2．
5. 等腰，等腰直角
【解析】
连接OP，根据轴对称的性质可得：
（1）OP=OE=OF，故△EOF一定是等腰三角形；
（2）∠AOE=∠AOP，∠BOF=∠BOP；
∴∠EOF=2（∠AOP+∠BOP）=2∠AOB；
当∠AOB=45°时，∠EOF=90°；故此时△EOF是等腰直角三角形．
故填等腰，等腰直角．
【】
三、解答题
1.【解析】（1）△ADC，△AMB，△BNC，△MNP，△ABE．理由如下：
∵∠ABC=60°，∠BAC=75°，AD，CF分别是BC，AB边上的高
∴∠DAC=45°，
又∵∠ACB=45°
∴△ADC为等腰三角形．
∵∠ABC的平分线BE分别交AD，CF于M，N
∴∠ABM=30°，
又∵∠BAM=30°
∴△AMB为等腰三角形．
由题意可知∵∠NBC=∠NCB=30°
∴△BNC为等腰三角形．
∠PMN=∠MNP=60°
∴△MNP为等腰三角形．
∵∠ABE=30°，∠BAC=75°
∴∠BEA=75°
∴△ABE为等腰三角形．
（2）在直角三角形BDM中，
∵MD=2cm，∠MBD=30°
∴BM=4cm
在等腰△AMB中，BM=AM
则AD=AM+MD=6cm，
在等腰直角三角形ADC中
AD=DC
则DC=6cm．
2. 【解析】∵∠NAC=43°，∠NBC=86°，
∴∠ACB=43°，
∴∠NAC=∠ACB，
∴BC=BA=15×（10-8）=15×2=30．
答：海岛B与灯塔C相距30海里．
四、证明题
1.【解析】证明：∵BD，CE是△ABC的高，
∴∠CEB=∠BDC=90°，
在Rt△BCE和Rt△CBD中，
∵，
∴Rt△BCE≌Rt△CBD（HL），
∴∠ABC=∠ACB，
∴△ABC是等腰三角形。21世纪教育网版权所有
2.【解析】证明：∵DC∥AB，AD=BC，∠A=60°，
∴∠ABC=∠A=60°，
又∵BD平分∠ABC，
∴∠ABD=∠CBD=∠ABC=30°，
∵DC∥AB，
∴∠BDC=∠ABD=30°，
∴∠CBD=∠CDB，
∴CB=CD，
∵CF⊥BD，
∴F为BD中点，
又∵DE⊥AB，
∴DF=BF=EF，
由∠ABD=30°，得∠BDE=60°，
∴△DEF为等边三角形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)