2.7探索勾股定理（2） 练习题

21世纪教育网 –中小学教育资源及组卷应用平台
探索勾股定理（2）
班级：___________姓名：___________得分：__________
一、选择题
1、下面各组数据能判断是直角三角形的是（　　）
A．三边长都为2 B．三边长分别为2，3，2
C．三边长分别为13，12，5 D．三边长分别为4，5，6
2. A、B、C分别表示三个村庄，AB=1300米，BC=500米，AC=1200米，在社会主义新农村建设中，为了丰富群众生活，拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（　　）21·cn·jy·com
A．AB中点 B．BC中点
C．AC中点 D．∠C的平分线与AB的交点
3. 三角形三条边的长有下面四组：①0.3、0.4、0.5；②2、5、6；③1、、1；④1、4、4．可构成直角三角形的有（　　）【来源：21·世纪·教育·网】
A．1组 B．2组 C．3组 D．4组
4. 如图所示，有一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，则这块地的面积为（　　）www-2-1-cnjy-com
A．24平方米 B．26平方米 C．28平方米 D．30平方米
5. 五根小木棒，其长度分别为7，15，20，24，25，现想把它们摆成两个直角三角形，图中正确的是（ ）2-1-c-n-j-y
二、填空题
1、若一个三角形的三边之比为5：12：13，且周长为60cm，则它的面积为______cm2．
2. 一个三角形的三边BC，AC，AB有如下关系：BC2=AC2+AB2，则Rt△ABC中的直角是______．21教育网
3. 已知|x-3|+|y-4|+（z-5）2=0，则由x，y，z为边的三角形的形状是______．
4. 如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120海里，乙巡逻艇每小时航行50海里，航向为北偏西40°，则甲巡逻艇的航向为北偏东( )度．【来源：21cnj*y.co*m】
5. 阅读以下解题过程：
已知a，b，c为△ABC的三边，且满足a2c2-b2c2=a4-b4，试判断△ABC的形状．
错∵a2c2-b2c2=a4-b4…（1），
∴c2（a2-b2）=（a2-b2）（a2+b2）…（2），
∴c2=a2+b2…（3）
问：
（1）上述解题过程，从哪一步开始发现错误请写出该步的代号______．
（2）错误的原因是______．
（3）本题正确的结论是______．【版权所有：21教育】
三、解答题
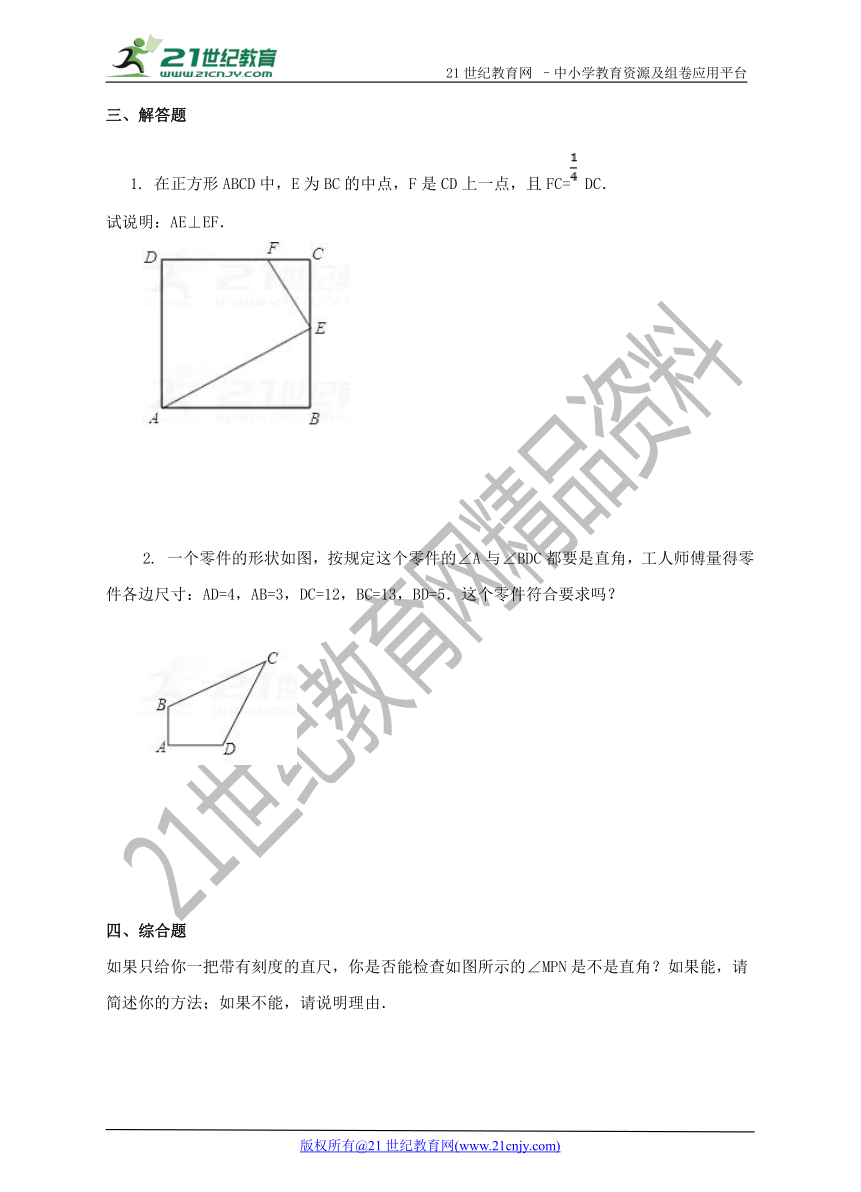
1. 在正方形ABCD中，E为BC的中点，F是CD上一点，且FC= DC．
试说明：AE⊥EF．
2. 一个零件的形状如图，按规定这个零件的∠A与∠BDC都要是直角，工人师傅量得零件各边尺寸：AD=4，AB=3，DC=12，BC=13，BD=5．这个零件符合要求吗？
四、综合题
如果只给你一把带有刻度的直尺，你是否能检查如图所示的∠MPN是不是直角？如果能，请简述你的方法；如果不能，请说明理由．21·世纪*教育网
参考答案
一、选择题
2、A
【解析】
∵AB2=1690000，BC2=250000，AC2=1440000，
∴BC2+AC2=AB2，
∴△ABC是直角三角形，
∴活动中心P应在斜边AB的中点．
故选A．21cnjy.com
3、B
【解析】①∵0.32+0.42=0.52，∴0.3、0.4、0.5可以构成直角三角形；
②22+52≠62，故2、5、6不能构成直角三角形；
③12+12=（）2，故1、、1可以构成直角三角形；
④12+42≠42，故1，4，4不能构成直角三角形．
故能构成直角三角形的有①③两个．
故选B．www.21-cn-jy.com
4.A
【解析】如图，连接AC．
由勾股定理可知
AC===5，
又∵AC2+BC2=52+122=132=AB2
∴△ABC是直角三角形
故所求面积=△ABC的面积-△ACD的面积=×5×12-×3×4=24（m2）．
故选A．21*cnjy*com
5.C
【解析】7 +24 =25
15 +20 =25 ,由勾股定理逆定理得答案C
二、填空题
1、120
【解析】设三边分别为5x，12x，13x，
则5x+12x+13x=60，
∴x=2，
∴三边分别为10cm，24cm，26cm，
∵102+242=262，∴三角形为直角三角形，
∴S=10×24÷2=120cm22·1·c·n·j·y
2、∠A
【解析】∵BC2=AB2+AC2，
∴△ABC是直角三角形，BC是斜边，∠A=90°．
故答案为：∠A．【出处：21教育名师】
3、直角三角形
【解析】根据题意得，x-3=0，y-4=0，z-5=0，
解得x=3，y=4，z=5，
∵x2+y2=42+32=25=z2，
∴此三角形是直角三角形．
故答案为：直角三角形．21教育名师原创作品
4.50
【解析】解：∵AC=120×=12海里，BC=50×=5海里
∵AC2+BC2=AB2
∴△ABC是直角三角形
∵∠CBA=50°
∴∠CAB=40°
∴甲的航向为北偏东50°．21*cnjy*com
5. ③，不能确定a2-b2是否为0，等腰三角形或直角三角形．
【解析】∵c2（a2-b2）=（a2-b2）（a2+b2）∴应有c2（a2-b2）-（a2-b2）（a2+b2）=0得到（a2-b2）[c2-（a2+b2）]=0，∴（a2-b2）=0或[c2-（a2+b2）]=0，即a=b或a2+b2=c2，∴根据等腰三角形得定义和勾股定理的逆定理，三角形为等腰三角形或直角三角形．故填③，不能确定a2-b2是否为0，等腰三角形或直角三角形．
【】
三、解答题
1.【解析】证明：连接AF，
设FC=a，则DC=DA=AB=BC=4a
所以DF=3a，CE=EB=2a．
由勾股定理得AF=5a，
EF=a，AE=2a从而由（a）2+（2a）2=（5a）2
即EF2+AE2=AF2
∴△AEF为直角三角形，斜边为AF，
故∠AEF=90°，
即AE⊥EF．
2. 【解析】
连结BD．
∵AD=4，AB=3，DC=12，BC=13，BD=5，
∴AB2+AD2=BD2，
BD2+DC2=BC2．
∴△ABD、△BDC是直角三角形．
∴∠A=90°，∠BDC=90°．
故这个零件符合要求．
四、综合题
【解析】能检查．
作法：如图所示，
（1）在射线PM上量取PA=3cm，确定A点，在射线PN上量取PB=4cm，确定点B．
（2）连接AB得△PAB．
（3）用刻度尺量取AB的长度，如果AB恰好等于5cm，则说明∠P是直角，否则∠P就不是直角．
理由：∵PA=3cm，PB=4cm，PA2+PB2=32+42=52．
若AB=5cm，则PA2+PB2=AB2，
根据勾股定理的逆定理可得△PAB是直角三角形，即∠P是直角．21世纪教育网版权所有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)