2.8直角三角形全等的判定 练习题

21世纪教育网 –中小学教育资源及组卷应用平台
直角三角形全等的判定
班级：___________姓名：___________得分：__________
一、选择题
1、下面说法不正确的是（ ）
A、有一角和一边对应相等的两个直角三角形全等
B、有两边对应相等的两个直角三角形全等
C、有两角对应相等的两个直角三角形全等
D、有两角和一边对应相等的两个直角三角形全等
2. 下列说法正确的有（　　）
①角平分线上任意一点到角两边的距离相等
②到一个角两边的距离相等的点在这个角的平分线上
③三角形三个角平分线的交点到三个顶点的距离相等
④三角形三条角平分线的交点到三边的距离相等．
A．1个 B．2个 C．3个 D．4个
3. 如图，P是∠AOB的平分线OC上一点（不与O重合），过P分别向角的两边作垂线PD、PE，垂足是D、E，连结DE，那么图中全等的直角三角形共有（　　）
A．3对 B．2对 C．1对 D．没有
4. 为了加快灾后重建的步伐，我市某镇要在三条公路围成的一块平地上修建一个砂石场，如图，要使这个砂石场到三条公路的距离相等，则可供选择的地址（　　）
A．仅有一处 B．有四处 C．有七处 D．有无数处
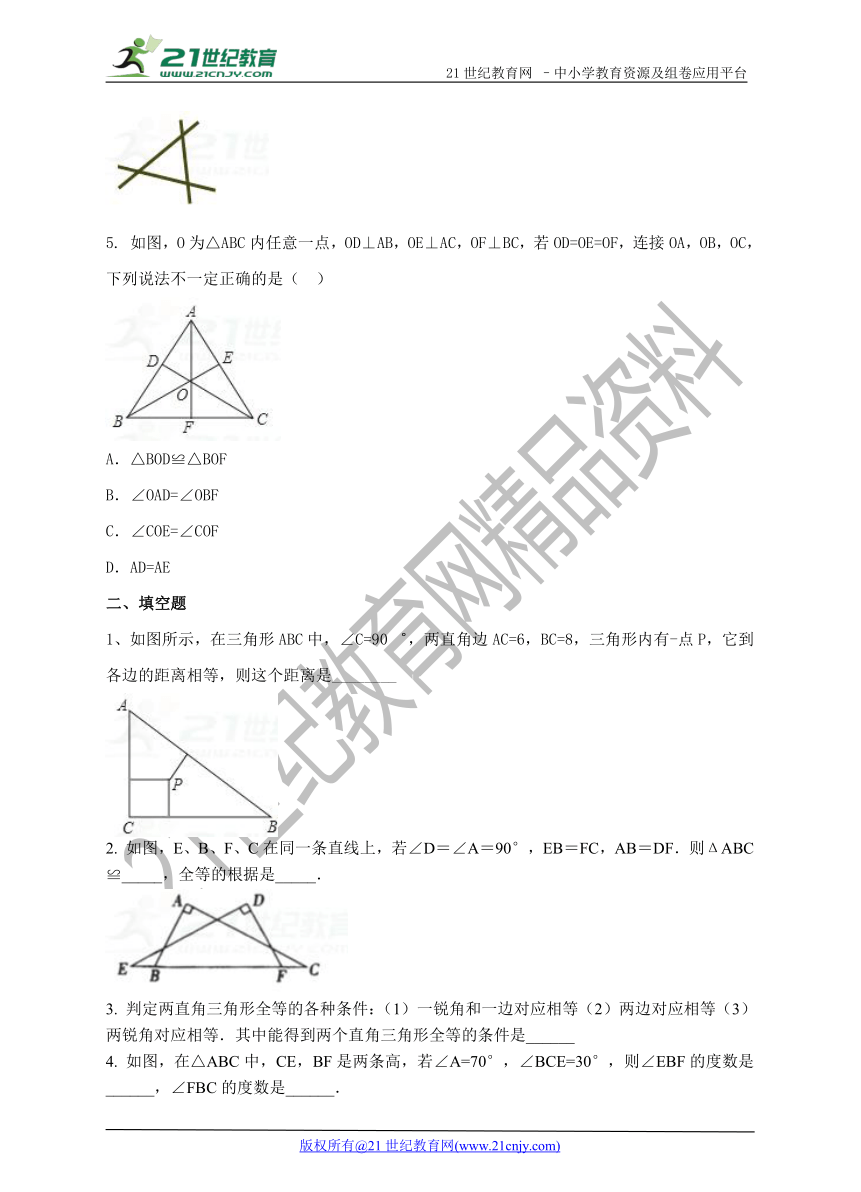
5. 如图，O为△ABC内任意一点，OD⊥AB，OE⊥AC，OF⊥BC，若OD=OE=OF，连接OA，OB，OC，下列说法不一定正确的是（　）21·cn·jy·com
A．△BOD≌△BOF
B．∠OAD=∠OBF
C．∠COE=∠COF
D．AD=AE
二、填空题
1、如图所示，在三角形ABC中，∠C=90゜，两直角边AC=6，BC=8，三角形内有-点P，它到各边的距离相等，则这个距离是________2·1·c·n·j·y
2. 如图，E、B、F、C在同一条直线上，若∠D＝∠A＝90°，EB＝FC，AB＝DF．则ΔABC≌_____，全等的根据是_____．【来源：21·世纪·教育·网】
3. 判定两直角三角形全等的各种条件：（1）一锐角和一边对应相等（2）两边对应相等（3）两锐角对应相等．其中能得到两个直角三角形全等的条件是______21*cnjy*com
4. 如图，在△ABC中，CE，BF是两条高，若∠A=70°，∠BCE=30°，则∠EBF的度数是______，∠FBC的度数是______．【来源：21cnj*y.co*m】
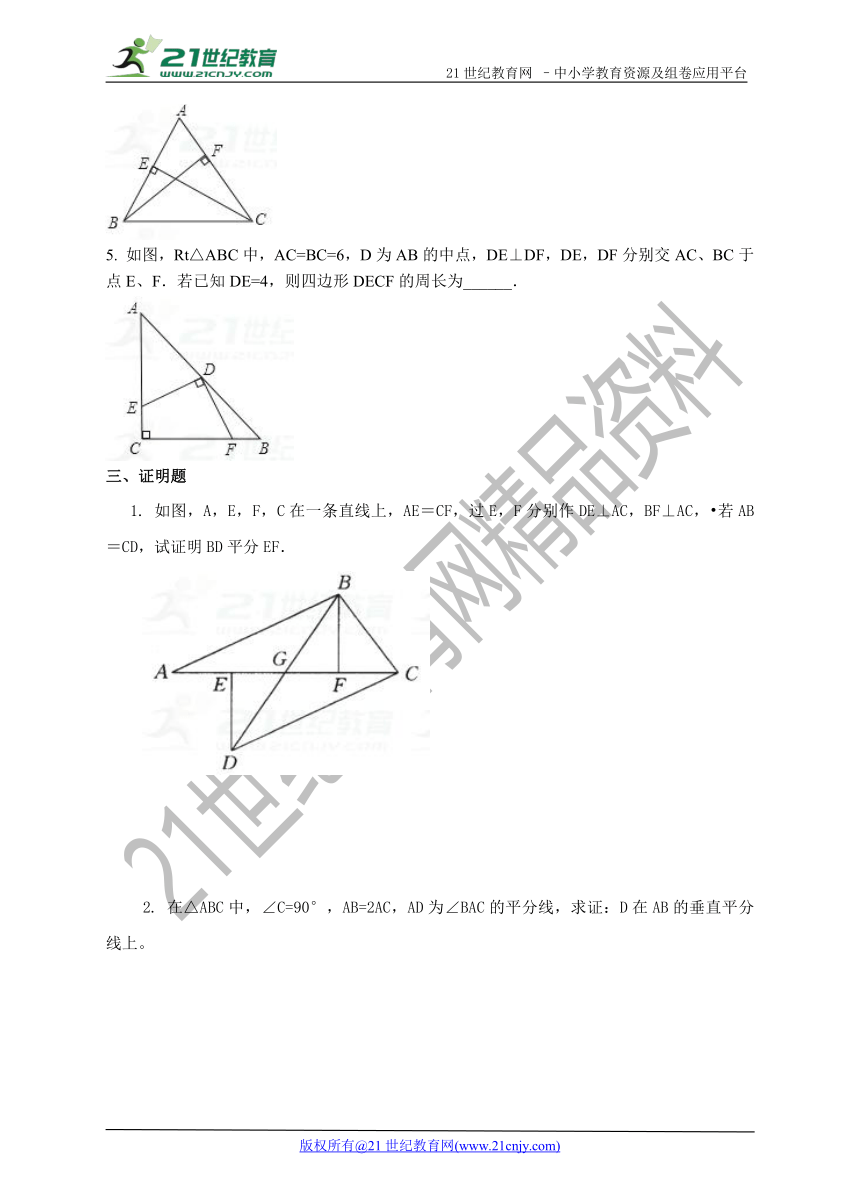
5. 如图，Rt△ABC中，AC=BC=6，D为AB的中点，DE⊥DF，DE，DF分别交AC、BC于点E、F．若已知DE=4，则四边形DECF的周长为______．【版权所有：21教育】
三、证明题
1. 如图，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC， 若AB＝CD，试证明BD平分EF．21教育名师原创作品
2. 在△ABC中，∠C=90°，AB=2AC，AD为∠BAC的平分线，求证：D在AB的垂直平分线上。www.21-cn-jy.com
四、操作题
如图，C，D是∠AOB内两点，求作一点P，使P到OA、OB的距离相等，并且PC=PD。
参考答案
一、选择题
1、C
【解析】A、∵直角三角形的斜边和一锐角对应相等，所以另一锐角必然相等，∴符合ASA定理，故本选项正确；2-1-c-n-j-y
B、两边对应相等的两个直角三角形全等，若是两条直角边，可以根据SAS判定全等，若是直角边与斜边，可根据HL判定全等．故本选项正确；【出处：21教育名师】
C、有两个锐角相等的两个直角三角形相似，故本选项错误；
D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理，可判定相等，故本选项正确．
故选C．
2、B
【解析】①角平分线上任意一点到角两边的距离相等，正确；
②应为，在角的内部到一个角两边的距离相等的点在这个角的平分线上，故本小题错误；
③三角形三个角平分线的交点到三个顶点的距离相等，错误；
④三角形三条角平分线的交点到三边的距离相等，正确；
综上所述，说法正确的是①④共2个．
故选B．
3、A
【解析】图中全等直角三角形有：Rt△ODP≌Rt△OEP、Rt△ODF≌Rt△OEF、Rt△FDP≌Rt△FEP．共3对．www-2-1-cnjy-com
故选A．
5.B
【解析】试题分析：∵OD⊥AB，OE⊥AC，OF⊥BC，OD=OE=OF，
∴O在∠ABC的角平分线上（∠DBO=∠FBO），∠ODB=∠OFB=90°，
∵在△BOD和△BOF中
∠BDO=∠BFO ∠DBO=∠FBO BO=BO
∴△BOD≌△BOF，正确，故本选项错误；
B、根据已知不能推出∠OAD=∠OBF，错误，故本选项正确；
C、∵OD⊥AB，OE⊥AC，OF⊥BC，OD=OE=OF，
∴O在∠ACB的角平分线上（∠FCO=∠ECO），∠OFC=∠OEC=90°，
∵在△COF和△COE中
∠CFO=∠CEO ∠FCO=∠ECO CO=CO
∴△COF≌△COE，
∴∠COE=∠COF，正确，故本选项错误；
D、∵OD⊥AB，OE⊥AC，
∴∠ADO=∠AEO=90°，
∵OD=OE，OA=OA，由勾股定理得：AE=AD，正确，故本选项错误；
故选B．
二、填空题
1、2
【解析】由勾股定理得：AB==10，∵在△ABC内有一点P，点P到各边的距离都相等，21世纪教育网版权所有
∴P为△ABC的内切圆的圆心，设切点为D、E、F，连接PD、PE、PF、PA、PC、PB，内切圆的半径为R，21·世纪*教育网
则由三角形面积公式得：×AC×BC=×AC×R+×BC×R+×AB×R，
∴6×8=6R+8R+10R，
R=2，
2、△DFE，HL
【解析】EB＋BF＝FC＋BF，即EF＝BC，斜边相等；
3、（1）和（2）
【解析】∵（1）一锐角与一边对应相等，
可利用AAS或ASA判定两直角三角形全等，
（2）两边对应相等，可利用HL或ASA判定两直角三角形全等；
（3）两锐角对应相等，缺少对应边相等这一条件，
所以不能判定两直角三角形全等．
故（1）和（2）．
4. 20°，40°
【解析】
在Rt△ABF中，∠A=70，CE，BF是两条高，
∴∠EBF=20°，∠ECA=20°，
又∵∠BCE=30°，
∴∠ACB=50°，
∴在Rt△BCF中∠FBC=40°．
故答案为：20°，40°．
5.14
【解析】连接CD．
∵Rt△ABC中，AC=BC=6，D为AB的中点，
∴CD⊥AB，∠ECD=∠DCB=∠B=45°，CD=BD，
∵DE⊥DF，
∠CDE=∠BDF，
在△CDE与△BDF中
∠ECD=∠B CD=BD ∠CDE=∠BDF
∴△CDE≌△BDF，
∴EC=FB，ED=FD，
∴四边形DECF的周长为：ED+DF+CF+CE=2ED+CF+FB=2ED+CB=2×4+6=14．
故答案为：14．
【】
三、解答题
1.【解析】证明∵DE⊥AC，BF⊥AC，∴∠DEG＝∠BFE＝90°．
∵AE＝CF，AE＋EF＝CF＋EF． 即AF＝CE．
在Rt△ABF和Rt△CDE中，
AB=CD,AF=CF，
∴Rt△ABF≌Rt△CDE（HL），∴BF＝DE．
在△BFG和△DEG中
∠BFG=∠DEG,∠BGF=∠DGE，BF=DE
∴△BFG≌△DEG（AAS），∴FG＝EG，即BD平分EF
2. 【解析】证明：∵在△ABC 中，∠C=90°，AB=2AC ，
∴∠BAC=60°，∠ABC=30°
∵AD 平分∠BAC，
∴∠BAD=30°
∴∠BAD=∠ABC
∴BD=AD
∴D在AB的垂直平分线上。21教育网
四、操作题
【解析】解：作法：
（1）作∠AOB的平分线OE；
（2）连CD，作CD的垂直平分线MN，与OE交于点P；
点P 即为所求的点，如图：21cnjy.com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)