6.1 几何图形一课一练

21世纪教育网 –中小学教育资源及组卷应用平台
6.1 几何图形一课一练
姓名：__________班级：__________学号：__________
1 、选择题（本大题共5小题）
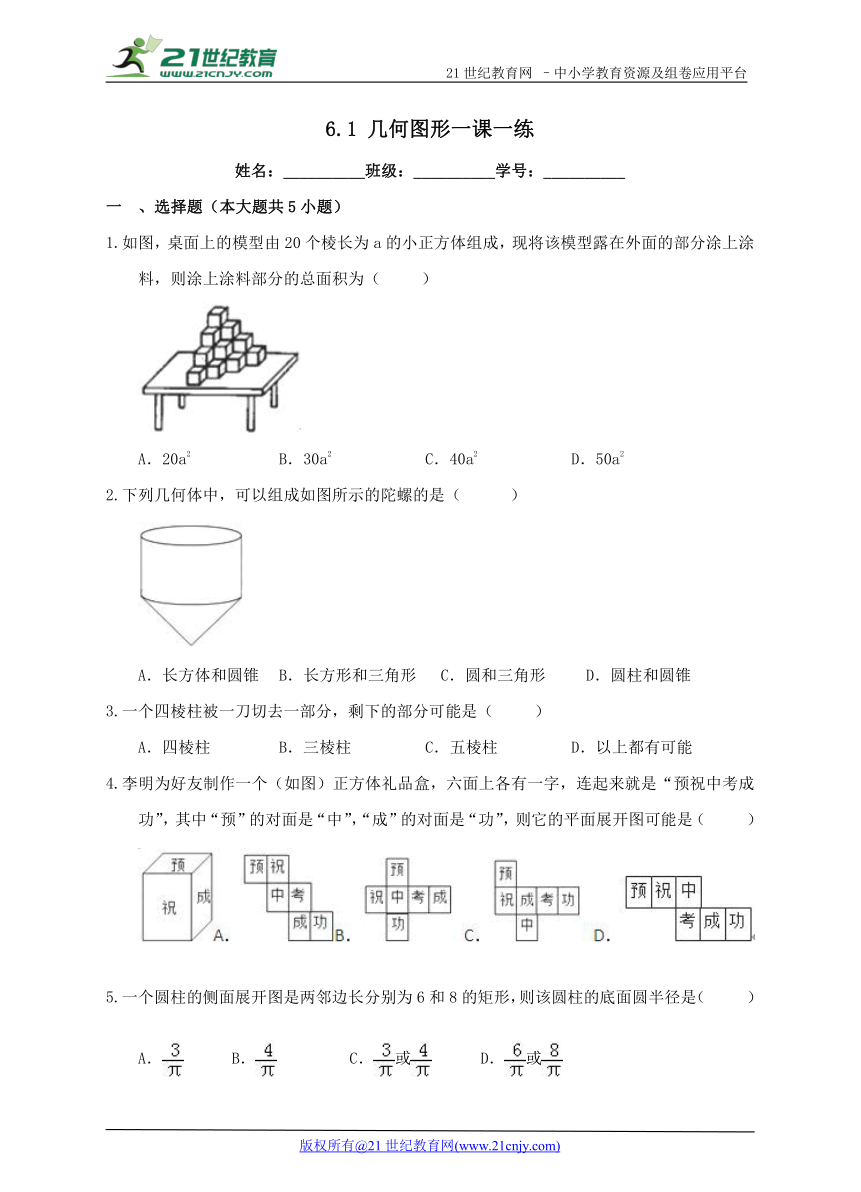
如图，桌面上的模型由20个棱长为a的小正方体组成，现将该模型露在外面的部分涂上涂料，则涂上涂料部分的总面积为（　 　）21世纪教育网版权所有
( http: / / www.21cnjy.com )
A．20a2 B．30a2 C．40a2 D．50a2
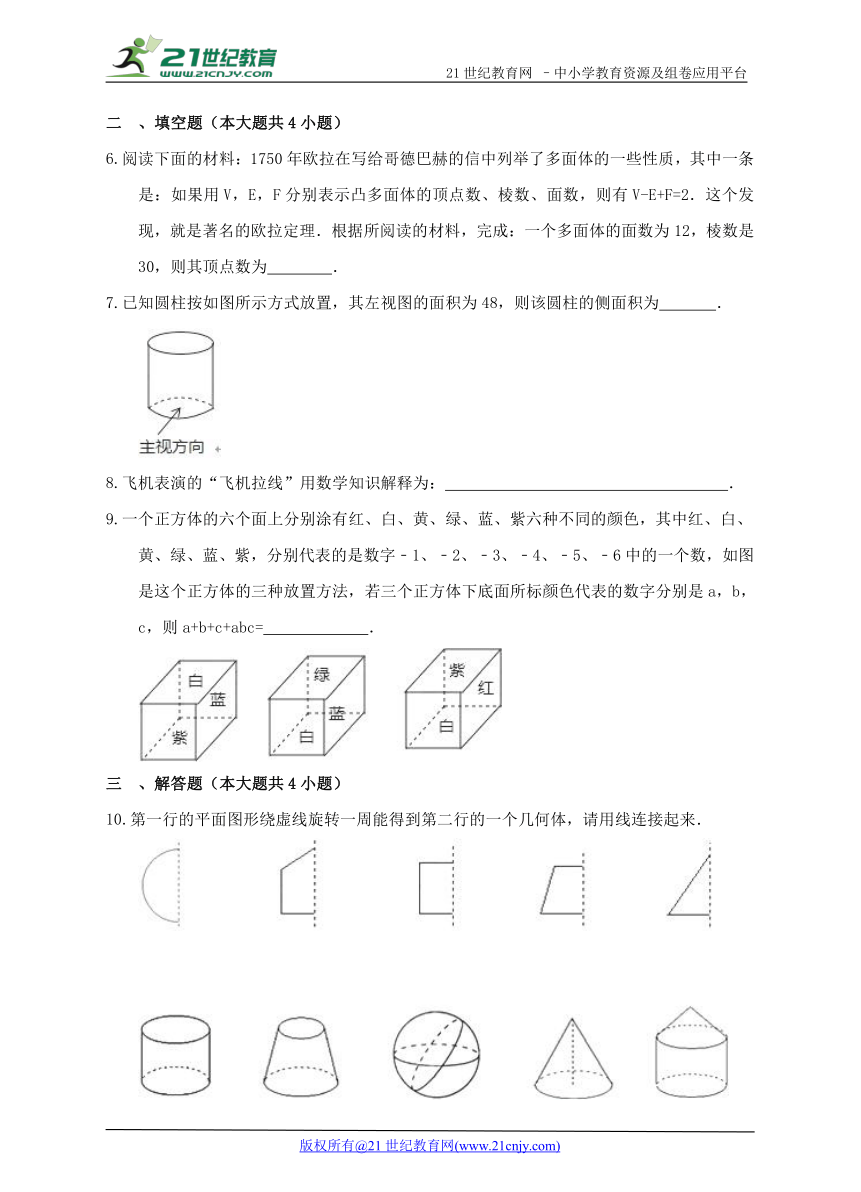
下列几何体中，可以组成如图所示的陀螺的是（ ）
( http: / / www.21cnjy.com )
A．长方体和圆锥 B．长方形和三角形 C．圆和三角形 D．圆柱和圆锥
一个四棱柱被一刀切去一部分，剩下的部分可能是（　 　）
A．四棱柱 B．三棱柱 C．五棱柱 D．以上都有可能
李明为好友制作一个（如图）正方体礼品盒 ( http: / / www.21cnjy.com )，六面上各有一字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（　 　）
( http: / / www.21cnjy.com )
一个圆柱的侧面展开图是两邻边长分别为6和8的矩形，则该圆柱的底面圆半径是（ ）
A． ( http: / / www.21cnjy.com ) B． ( http: / / www.21cnjy.com ) C． ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com ) D． ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com )
1 、填空题（本大题共4小题）
阅读下面的材料：1750年欧拉在写给哥德 ( http: / / www.21cnjy.com )巴赫的信中列举了多面体的一些性质，其中一条是：如果用V，E，F分别表示凸多面体的顶点数、棱数、面数，则有V-E+F=2．这个发现，就是著名的欧拉定理．根据所阅读的材料，完成：一个多面体的面数为12，棱数是30，则其顶点数为 ．21·cn·jy·com
已知圆柱按如图所示方式放置，其左视图的面积为48，则该圆柱的侧面积为　 　．
( http: / / www.21cnjy.com )
飞机表演的“飞机拉线”用数学知识解释为：　 　　 　　 　　 　　 　．
一个正方体的六个面上分别涂有红、白、黄、 ( http: / / www.21cnjy.com )绿、蓝、紫六种不同的颜色，其中红、白、黄、绿、蓝、紫，分别代表的是数字﹣1、﹣2、﹣3、﹣4、﹣5、﹣6中的一个数，如图是这个正方体的三种放置方法，若三个正方体下底面所标颜色代表的数字分别是a，b，c，则a+b+c+abc=　 　．2·1·c·n·j·y
( http: / / www.21cnjy.com )
1 、解答题（本大题共4小题）
第一行的平面图形绕虚线旋转一周能得到第二行的一个几何体，请用线连接起来．
( http: / / www.21cnjy.com )
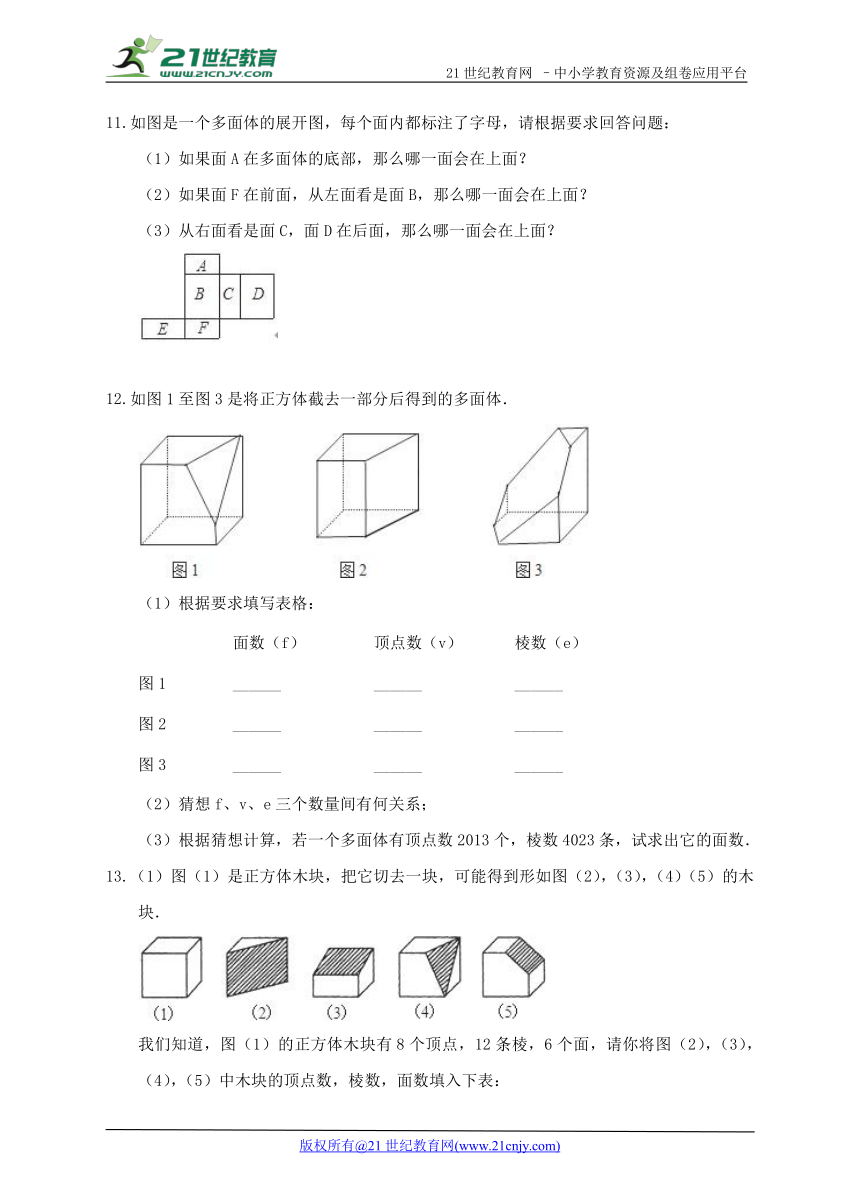
如图是一个多面体的展开图，每个面内都标注了字母，请根据要求回答问题：
（1）如果面A在多面体的底部，那么哪一面会在上面？
（2）如果面F在前面，从左面看是面B，那么哪一面会在上面？
（3）从右面看是面C，面D在后面，那么哪一面会在上面？
( http: / / www.21cnjy.com )
如图1至图3是将正方体截去一部分后得到的多面体．
( http: / / www.21cnjy.com )
（1）根据要求填写表格：
面数（f） 顶点数（v） 棱数（e）
图1 ______ ______ ______
图2 ______ ______ ______
图3 ______ ______ ______
（2）猜想f、v、e三个数量间有何关系；
（3）根据猜想计算，若一个多面体有顶点数2013个，棱数4023条，试求出它的面数．
（1）图（1）是正方体木块，把它切去一块，可能得到形如图（2），（3），（4）（5）的木块．
( http: / / www.21cnjy.com )
我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入下表：21·世纪*教育网
图 顶点数 棱数 面数
（1） 8 12 6
（2）
（3）
（4）
（5）
（2）观察上表，请你归纳上 ( http: / / www.21cnjy.com )述各种木块的顶点数，棱数，面数之间的数量关系，这种数量关系是：______．
（3）如图，是用虚线画出的正方体木块，请你想象一种与图（2）～（5）不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为______，棱数为______，面数为______．这与你（2）题中所归纳的关系是否相符？
( http: / / www.21cnjy.com )
参考答案
1 、选择题
【分析】解此类题需从正面、上面，后面，左面，右面等多个角度进行观察和解答．
解：从正面、上面，后面，左面，右面看都有10个正方形，则共有50个正方形，因为每个正方形的面积为a2，则涂上涂料部分的总面积为50a2．21cnjy.com
故选D．
【分析】图中的几何体上面是圆柱，下面 ( http: / / www.21cnjy.com )是圆锥，都是旋转体，圆柱是由长方形旋转而成的，圆锥是由三角形旋转而成的，由此得出答案．
解：如图所示的陀螺的是由长方形和三角形旋转而成的．
故选：B．【来源：21·世纪·教育·网】
【分析】三棱柱、四棱柱、五棱柱都有可能，关键是看切的位置．
解：三棱柱、四棱柱、五棱柱都有可能．
故选D．
( http: / / www.21cnjy.com )
【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点，对各选项分析即可作答．
解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
A．“预”的对面是“考”，“成”的对面是“祝”，故本选项错误；
B、“预”的对面是“功”，“成”的对面是“祝”，故本选项错误；
C、“预”的对面是“中”，“成”的对面是“功”，故本选项正确；
D、“预”的对面是“中”，“成”的对面是“祝”，故本选项错误．
故选C．
【分析】分8或6为底面周长两种情况解答
解： 分两种情况，8为底面周长，6为圆柱的高，此时底面半径为 ( http: / / www.21cnjy.com )；6为底面周长，8为圆柱的高，此时底面半径为 ( http: / / www.21cnjy.com )．www.21-cn-jy.com
故答案选C．
二、填空题
【分析】直接把面数、棱数代入公式，即可求得顶点数．
解：由题意可得，V-30+12=2，
解得V=20．
故答案为：20www-2-1-cnjy-com
【分析】先由左视图的面积=底面直径×高，得出底面直径，再根据侧面积=底面周长×高即可求解．
解：设圆柱的高为h，底面直径为d，
则dh=48，
解得d= ( http: / / www.21cnjy.com )，
所以侧面积为：π d h=π× ( http: / / www.21cnjy.com )×h=48π．
故答案为48π．
【分析】飞机在空中表演，飞机可看作一个点，则“飞机拉线”用数学知识解释为：点动成线．
解：飞机表演的“飞机拉线”用数学知识解释为：点动成线．
故答案为点动成线．
【分析】先根据图中正方形的摆放方 ( http: / / www.21cnjy.com )式可知与白色面相邻的面有紫、蓝、绿、红，然后再确定出其中相对的面，从而得出a、b、c的值，最后代入计算即可．
解：∵根据图形可知：白色面相邻的面有紫、蓝、绿、红，
∴“紫”与“绿”是对面，“红”与“蓝”是对面，“白”与“黄”是对面．
∴第一个正方体的底面是黄色，第二个正方体的底面是紫色，第三个正方体的底面是绿色．
∴a=﹣3，b=﹣6，c=﹣4．
∴a+b+c+abc=（﹣3）+（﹣6）+（﹣4）+（﹣3）×（﹣6）×（﹣4）=﹣13+（﹣72）=﹣85．2-1-c-n-j-y
故答案为：﹣85．
三、解答题
【分析】根据面动成体结合常见立体图形的形状连接即可．
解：连接如图．
( http: / / www.21cnjy.com )
【分析】利用长方体及其表面展开图 ( http: / / www.21cnjy.com )的特点解题．这是一个长方体的平面展开图，共有六个面，其中面“A”与面“F”相对，面“B”与面“D”相对，面“C”与面“E”相对．
解：这是一个长方体的平面展开图，共有六个面，其中面“A”与面“F”相对，面“B”与面“D”相对，面“C”与面“E”相对．21教育网
（1）面F会在上面；
（2）面C会在上面；
（3）面A会在上面．
【分析】（1）根据图形数出即可．
（2）根 ( http: / / www.21cnjy.com )据（1）中结果得出f+v-e=2．
（3）代入f+v-e=2求出即可．
解：（1）题1，面数f=7，顶点数v=9，棱数e=14，
题2，面数f=6，顶点数v=8，棱数e=12，
题3，面数f=6，顶点数v=10，棱数e=14，
故答案为：7，9，14.6，8，12，6，10，14．21*cnjy*com
（2）f+v-e=2．
（3）∵v=2013，e=4023，f+v-e=2
∴f+2013-4023=2，
f=2012，
即它的面数是2012．【出处：21教育名师】
【分析】（1）只要将图（ ( http: / / www.21cnjy.com )2）、（3）、（4）、（5）各个木块的顶点数、棱数、面数数一下就行；数的时候要注意：图中不能直接看到的那一部分不要遗漏，也不要重复，可通过想象计数，正确填入表内；
（2）通过观察找出每个图中“顶点数、棱数、面数”之间隐藏着的数量关系，这个数量关系用公式表示出来即可．
（3）按要求作出图形，注意是与图②～⑤不同的切法，然后数出该木块的顶点数，棱数和面数即可．
解：（1）见表：【版权所有：21教育】
图 顶点数 棱 数 面 数
（2） 6 9 5
（3） 8 1 2 6
（4） 8 1 3 7
（5） 1 O 1 5 7
（2）观察上表，即可归纳上述各种木块的顶点数、棱数、面数之间的数的关系是：
顶点数+面数=棱数+2．【来源：21cnj*y.co*m】
（3）如切过之后为一长方体，所画图形如下所示： ( http: / / www.21cnjy.com )
则该木块的顶点数为8，棱数为12，面数为6．
故答案为：（2）顶点数+面数=棱数+2；（3）8，12，6．21教育名师原创作品
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)