2017年浙教版七年级数学上册6《几何图形初步》课后练习含答案解析
文档属性
| 名称 | 2017年浙教版七年级数学上册6《几何图形初步》课后练习含答案解析 | 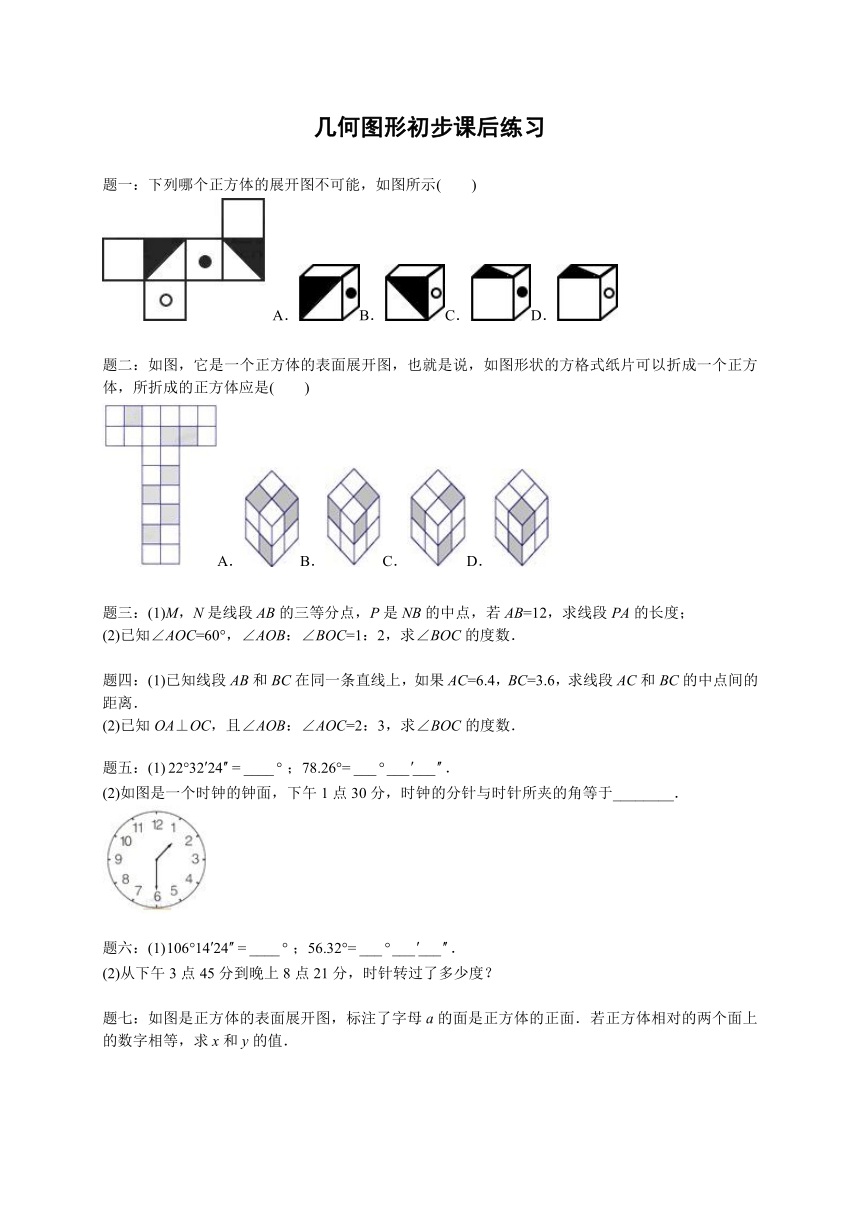 | |
| 格式 | zip | ||
| 文件大小 | 262.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-18 10:33:21 | ||
图片预览


文档简介
几何图形初步课后练习
下列哪个正方体的展开图不可能,如图所示( )
A.B.C.D.
如图,它是一个正方体的表面展开图,也就是说,如图形状的方格式纸片可以折成一个正方体,所折成的正方体应是( )
A.B.C.D.
(1)M,N是线段AB的三等分点,P是NB的中点,若AB=12,求线段PA的长度;
(2)已知∠AOC=60°,∠AOB:∠BOC=1:2,求∠BOC的度数.
(1)已知线段AB和BC在同一条直线上,如果AC=6.4,BC=3.6,求线段AC和BC的中点间的距离.
(2)已知OA⊥OC,且∠AOB:∠AOC=2:3,求∠BOC的度数.
(1)=;78.26°=.
(2)如图是一个时钟的钟面,下午1点30分,时钟的分针与时针所夹的角等于________.
(1)=;56.32°=.
(2)从下午3点45分到晚上8点21分,时针转过了多少度?
如图是正方体的表面展开图,标注了字母a的面是正方体的正面.若正方体相对的两个面上的数字相等,求x和y的值.
如图是一个正方体的表面展开图,请回答下列问题: (1)与面B、C相对的面分别是____、____; (2)若A=a3+a2b+3,B=a2b-3,C=a3-1,D=-(a2b-6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
期中期末串讲--几何图形初步
课后练习参考答案
B.
详解:根据图示可知与空心圆相邻的是白色的三角形,和实心圆相邻的是白色的三角形和白色的正方形.故不可能的是B.故选B.
D.
详解:根据展开图可得出正方体有两底面是两阴影小正方体相连接组成的图案,符合要求的只有A、D,但对角线相连部分,不可能与正方形再次相连,则A错误.故选D.
10或8;40°或120°.
详解:(1)因为M,N是线段AB的三等分点,所以NB=AB=, ①如图1,当N在靠近B的一端时,∵P是NB的中点,
∴PB=NB=2,∴PA=12-2=10; ②如图2,当N在靠近A的一端时,∵P是NB的中点,
∴P与M重合,∴PA=12-4=8. 故PA=10或8.
(2)①如图1,当OB在∠AOC内时, ∵∠AOC=60°,∠AOB:∠BOC=1:2,
∴∠BOC=×60°= 40°; ②如图2,当OB在∠AOC外时,
∵∠AOC=60°,∠AOB:∠BOC=1:2,
∴∠BOC=2∠AOC=2×60°=120°. 故∠BOC的度数是40°或120°.
1.4或5;30°或150°.
详解:(1)∵M为AC的中点,AC=6.4,∴CM=AC=3.2, ∵N为BC的中点,BC=3.6,∴CN=BC=1.8, 分为以下两种情况: ①如图1,当B在线段AC上时,MN=CM-CN=3.2-1.8=1.4;
②如图2,当B在AC的延长线时,MN=CM+CN=3.2+1.8=5.
故线段AC和BC的中点间的距离是1.4或5.
(2)∵OA⊥OC,∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.
①如图1,当在∠AOC内时,∠BOC=90°-60°=30°;
②如图2,当在∠AOC外时,∠BOC=90°+60°=150°.
故∠BOC的度数是30°或150°.
22.54°,;135°.
详解:(1)÷60=,÷60=0.54°,则=22.54°;
0.26×60=15.6,0.6×60=36,则78.26°=.
(2)由钟面平均分成12份,得每份30°,于是30°×(4+)=30°×=135°.
答:时钟的分针与时针所夹的角等于135°.
106.24°,;138°.
详解:(1)÷60=,÷60=0.24°,=106.24°;
0.32°×60=,×60=,则56.32°=.
(2)8时21分=8.35时,3时45分=3.75时,则8.35-3.75= 4.6(时),
由钟面平均分成12份,得每份30°,于是30°×4.6=138°.
答:时针转过了138°.
1,-1.
详解:正方体的表面展开图,相对的面之间一定相隔一个正方形, 所以,y+2与2x-1是相对面,2y与x-3是相对面. ∵正方体相对的两个面上的数字相等, ∴,整理,得, ①×2-②,得3x=3,解得x=1, 把x=1代入①,得y=-1, 所以,方程组的解是.
F、E;-a2b+7,a3-a2b+9.
详解:(1)由图可得:面A和面D相对,面B和面F,相对面C和面E相对, (2)由题意得,A+D=B+F=C+E, 代入可得a3+a2b+3+[-(a2b-6)]=a2b-3+F, a3+a2b+3+[-(a2b-6)]=a3-1+E, 解得F=a3-a2b+9,E=-a2b+7.
下列哪个正方体的展开图不可能,如图所示( )
A.B.C.D.
如图,它是一个正方体的表面展开图,也就是说,如图形状的方格式纸片可以折成一个正方体,所折成的正方体应是( )
A.B.C.D.
(1)M,N是线段AB的三等分点,P是NB的中点,若AB=12,求线段PA的长度;
(2)已知∠AOC=60°,∠AOB:∠BOC=1:2,求∠BOC的度数.
(1)已知线段AB和BC在同一条直线上,如果AC=6.4,BC=3.6,求线段AC和BC的中点间的距离.
(2)已知OA⊥OC,且∠AOB:∠AOC=2:3,求∠BOC的度数.
(1)=;78.26°=.
(2)如图是一个时钟的钟面,下午1点30分,时钟的分针与时针所夹的角等于________.
(1)=;56.32°=.
(2)从下午3点45分到晚上8点21分,时针转过了多少度?
如图是正方体的表面展开图,标注了字母a的面是正方体的正面.若正方体相对的两个面上的数字相等,求x和y的值.
如图是一个正方体的表面展开图,请回答下列问题: (1)与面B、C相对的面分别是____、____; (2)若A=a3+a2b+3,B=a2b-3,C=a3-1,D=-(a2b-6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
期中期末串讲--几何图形初步
课后练习参考答案
B.
详解:根据图示可知与空心圆相邻的是白色的三角形,和实心圆相邻的是白色的三角形和白色的正方形.故不可能的是B.故选B.
D.
详解:根据展开图可得出正方体有两底面是两阴影小正方体相连接组成的图案,符合要求的只有A、D,但对角线相连部分,不可能与正方形再次相连,则A错误.故选D.
10或8;40°或120°.
详解:(1)因为M,N是线段AB的三等分点,所以NB=AB=, ①如图1,当N在靠近B的一端时,∵P是NB的中点,
∴PB=NB=2,∴PA=12-2=10; ②如图2,当N在靠近A的一端时,∵P是NB的中点,
∴P与M重合,∴PA=12-4=8. 故PA=10或8.
(2)①如图1,当OB在∠AOC内时, ∵∠AOC=60°,∠AOB:∠BOC=1:2,
∴∠BOC=×60°= 40°; ②如图2,当OB在∠AOC外时,
∵∠AOC=60°,∠AOB:∠BOC=1:2,
∴∠BOC=2∠AOC=2×60°=120°. 故∠BOC的度数是40°或120°.
1.4或5;30°或150°.
详解:(1)∵M为AC的中点,AC=6.4,∴CM=AC=3.2, ∵N为BC的中点,BC=3.6,∴CN=BC=1.8, 分为以下两种情况: ①如图1,当B在线段AC上时,MN=CM-CN=3.2-1.8=1.4;
②如图2,当B在AC的延长线时,MN=CM+CN=3.2+1.8=5.
故线段AC和BC的中点间的距离是1.4或5.
(2)∵OA⊥OC,∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.
①如图1,当在∠AOC内时,∠BOC=90°-60°=30°;
②如图2,当在∠AOC外时,∠BOC=90°+60°=150°.
故∠BOC的度数是30°或150°.
22.54°,;135°.
详解:(1)÷60=,÷60=0.54°,则=22.54°;
0.26×60=15.6,0.6×60=36,则78.26°=.
(2)由钟面平均分成12份,得每份30°,于是30°×(4+)=30°×=135°.
答:时钟的分针与时针所夹的角等于135°.
106.24°,;138°.
详解:(1)÷60=,÷60=0.24°,=106.24°;
0.32°×60=,×60=,则56.32°=.
(2)8时21分=8.35时,3时45分=3.75时,则8.35-3.75= 4.6(时),
由钟面平均分成12份,得每份30°,于是30°×4.6=138°.
答:时针转过了138°.
1,-1.
详解:正方体的表面展开图,相对的面之间一定相隔一个正方形, 所以,y+2与2x-1是相对面,2y与x-3是相对面. ∵正方体相对的两个面上的数字相等, ∴,整理,得, ①×2-②,得3x=3,解得x=1, 把x=1代入①,得y=-1, 所以,方程组的解是.
F、E;-a2b+7,a3-a2b+9.
详解:(1)由图可得:面A和面D相对,面B和面F,相对面C和面E相对, (2)由题意得,A+D=B+F=C+E, 代入可得a3+a2b+3+[-(a2b-6)]=a2b-3+F, a3+a2b+3+[-(a2b-6)]=a3-1+E, 解得F=a3-a2b+9,E=-a2b+7.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
