第二章 直线与圆的位置关系单元检测A卷
文档属性
| 名称 | 第二章 直线与圆的位置关系单元检测A卷 |  | |
| 格式 | doc | ||
| 文件大小 | 831.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-18 20:19:35 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
直线和园的位置关系单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共10小题)
1.已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点共有( )21cnjy.com
A.1个 B.2个 C.3个 D.4个
2.已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么( )
A.0<OP<5 B.OP=5 C.OP>5 D.OP≥5
3.有下列结论:(1)平分弦的直径垂直于 ( http: / / www.21cnjy.com )弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
4.已知OA平分∠BOC,P是OA上一点,以P为圆心的⊙P与OC相切,则⊙P与OB的位置关系为( )
A.相离 B.相切 C.相交 D.不能确定
5.已知△ABC为锐角三角形,⊙O经过点B ( http: / / www.21cnjy.com ),C,且与边AB,AC分别相交于点D,E.若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的( )
A.内心 B.外心 C.重心 D.垂心
6.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
( http: / / www.21cnjy.com )
A.120° B.60° C.30° D.45°
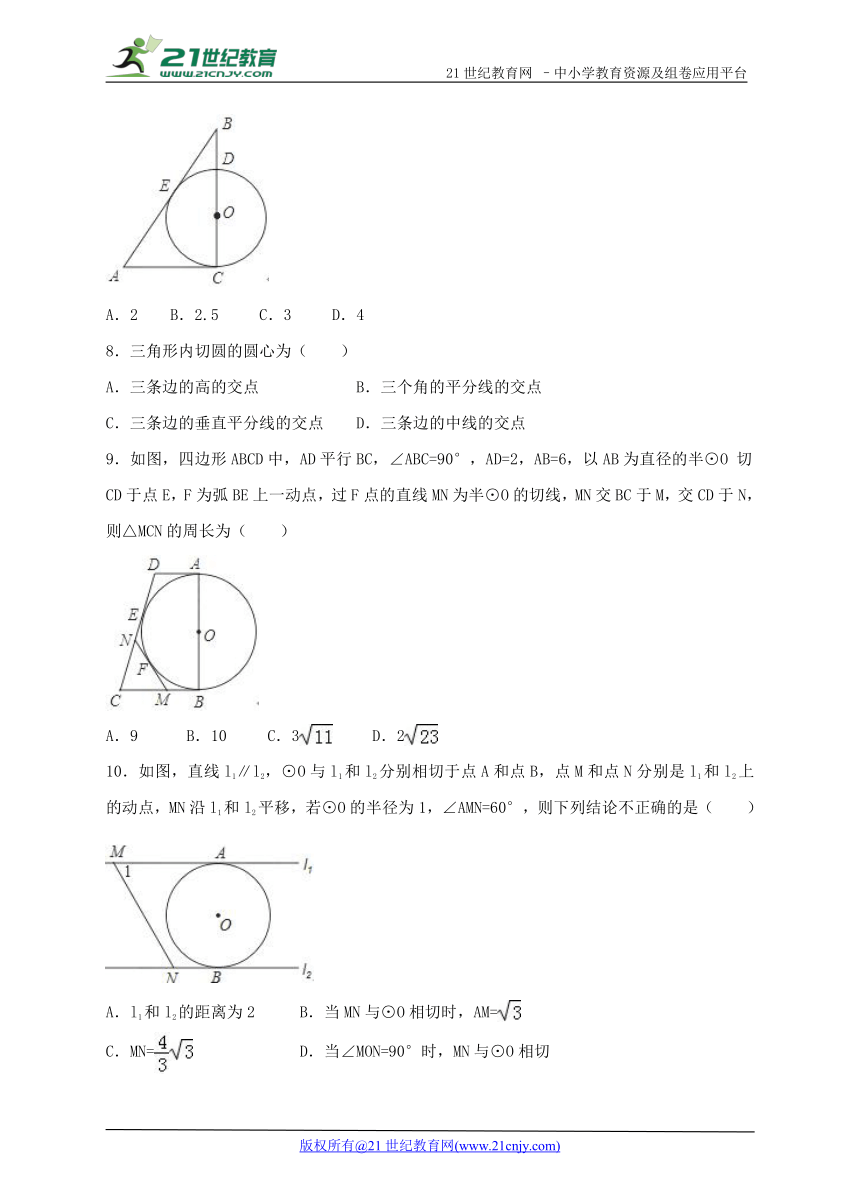
7.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,CD为直径的⊙O与AB相切于E,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A.2 B.2.5 C.3 D.4
8.三角形内切圆的圆心为( )
A.三条边的高的交点 B.三个角的平分线的交点
C.三条边的垂直平分线的交点 D.三条边的中线的交点
9.如图,四边形ABCD中,AD平行BC, ( http: / / www.21cnjy.com )∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
( http: / / www.21cnjy.com )
A.9 B.10 C.3 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
10.如图,直线l1∥l2 ( http: / / www.21cnjy.com ),⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )
( http: / / www.21cnjy.com )
A.l1和l2的距离为2 B.当MN与⊙O相切时,AM= ( http: / / www.21cnjy.com )
C.MN= ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) D.当∠MON=90°时,MN与⊙O相切
二.填空题(共6小题)
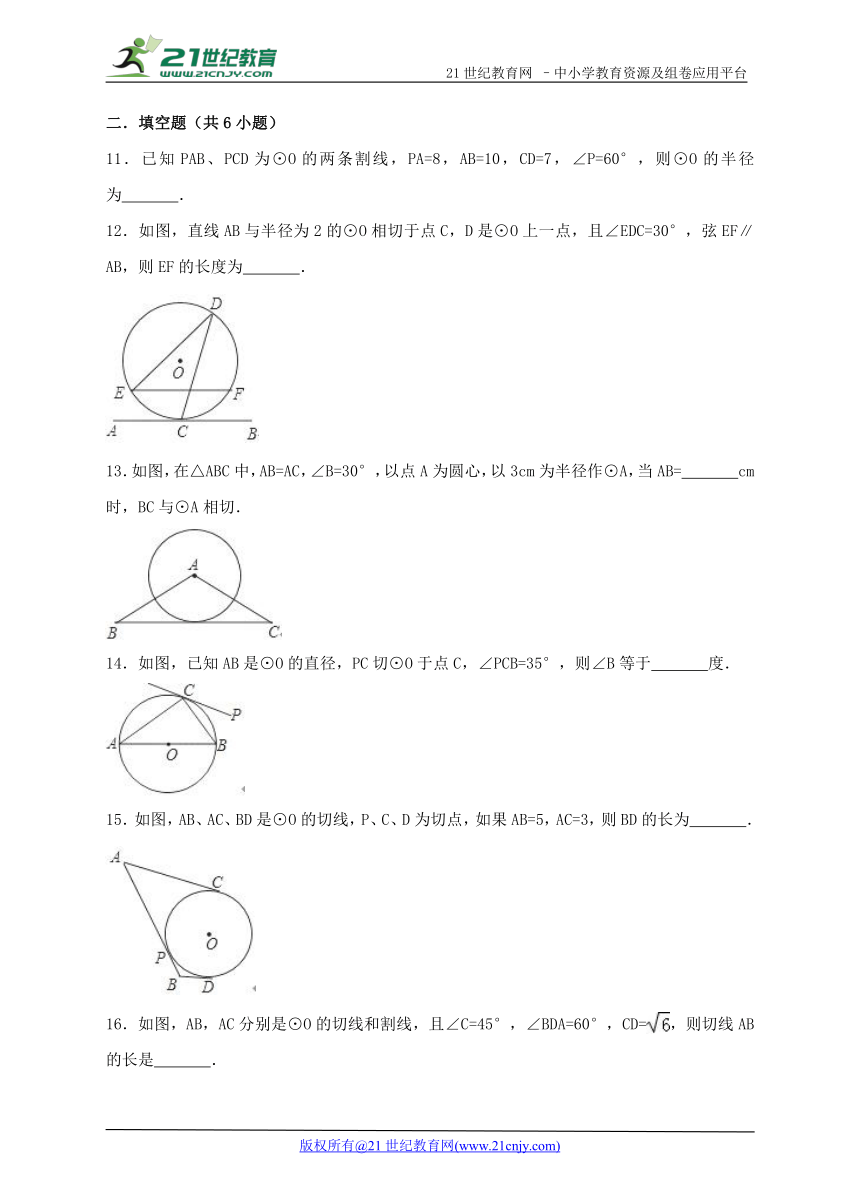
11.已知PAB、PCD为⊙O的两条割线,PA=8,AB=10,CD=7,∠P=60°,则⊙O的半径为 .
12.如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
13.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB= cm时,BC与⊙A相切.
( http: / / www.21cnjy.com )
14.如图,已知AB是⊙O的直径,PC切⊙O于点C,∠PCB=35°,则∠B等于 度.
( http: / / www.21cnjy.com )
15.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
( http: / / www.21cnjy.com )
16.如图,AB,AC分别是⊙O的切线和割线,且∠C=45°,∠BDA=60°,CD= ( http: / / www.21cnjy.com ),则切线AB的长是 .
( http: / / www.21cnjy.com )
三.解答题(共8小题)
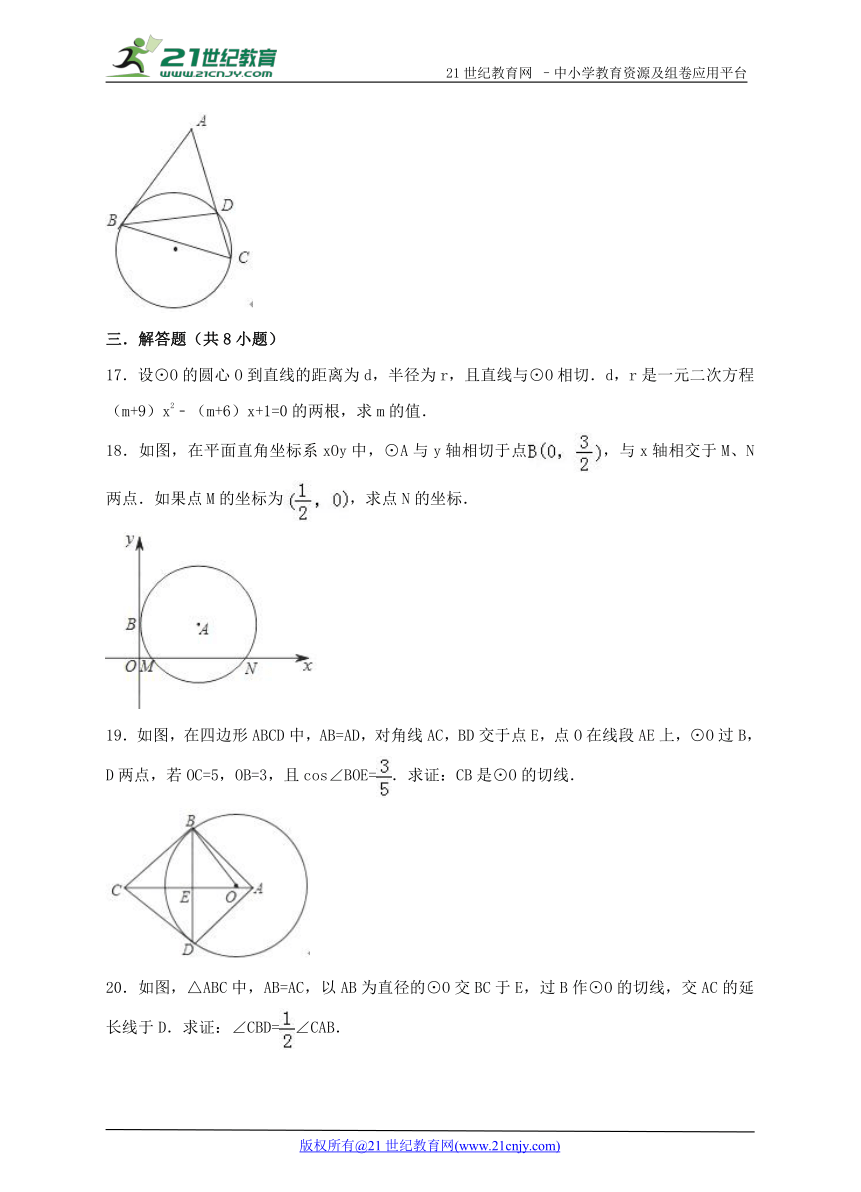
17.设⊙O的圆心O到直线的距离为d, ( http: / / www.21cnjy.com )半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2﹣(m+6)x+1=0的两根,求m的值.
18.如图,在平面直角坐标系xOy中,⊙A与y轴相切于点 ( http: / / www.21cnjy.com ),与x轴相交于M、N两点.如果点M的坐标为 ( http: / / www.21cnjy.com ),求点N的坐标.
( http: / / www.21cnjy.com )
19.如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE= ( http: / / www.21cnjy.com ).求证:CB是⊙O的切线.
( http: / / www.21cnjy.com )
20.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD= ( http: / / www.21cnjy.com )∠CAB.
( http: / / www.21cnjy.com )
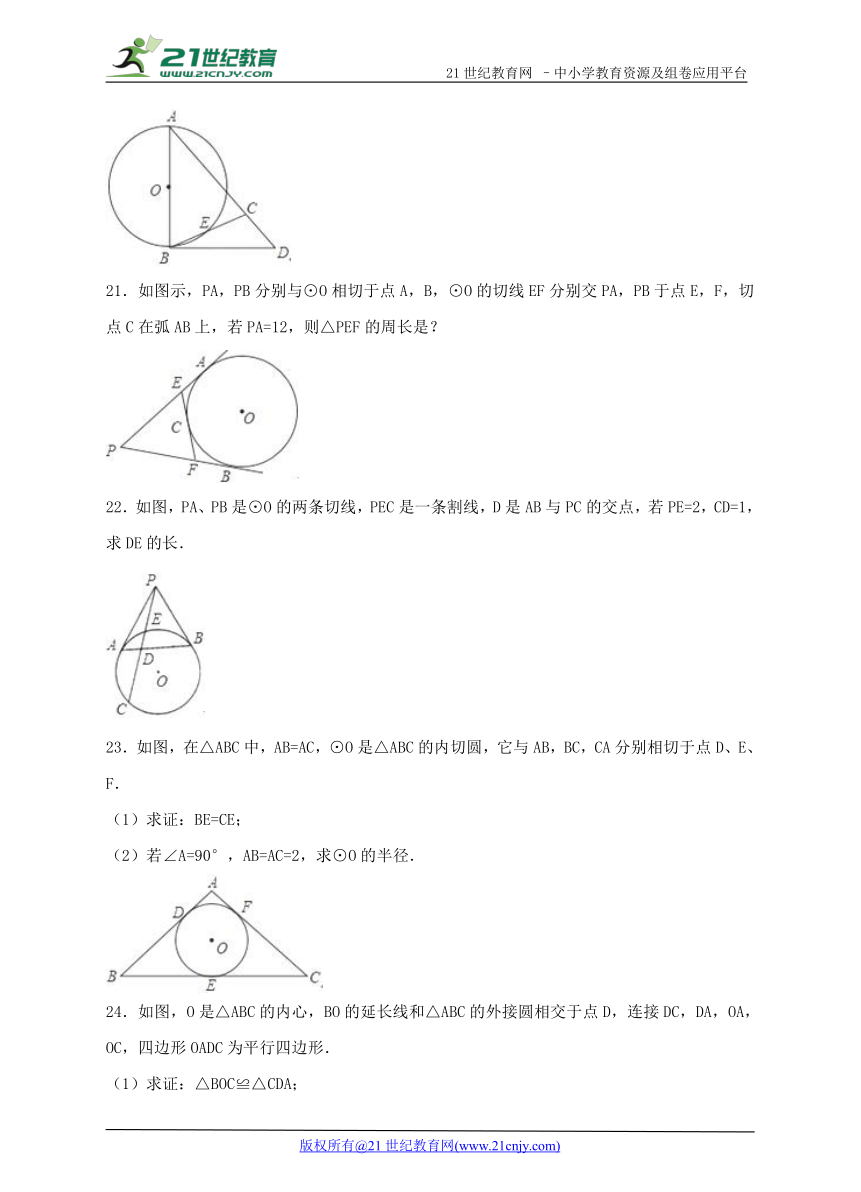
21.如图示,PA,PB分别与⊙O ( http: / / www.21cnjy.com )相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
( http: / / www.21cnjy.com )
22.如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.
( http: / / www.21cnjy.com )
23.如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
( http: / / www.21cnjy.com )
24.如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共10小题)
1. 【分析】根据平行线间的距离相等,先过点D作AB⊥OC,即可求得⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点的个数.21世纪教育网版权所有
解:如图,
∵⊙O的半径为5,点O到直线l的距离为3,
∴CE=2,
过点D作AB⊥OC,垂足为D,交⊙O于A、B两点,且DE= ( http: / / www.21cnjy.com ),
∴⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点在直线l的左边和右边各有两个,共四个,
故选D.
( http: / / www.21cnjy.com )
2.【分析】由⊙O的半径是5,直线 ( http: / / www.21cnjy.com )l是⊙O的切线,P是l上的任一点,可得当P与切点重合时,OP=5,当P与切点不重合时,OP>5,继而求得答案.21教育网
解:∵⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,
∴当P与切点重合时,OP=5,
当P与切点不重合时,OP>5,
∴OP≥5.
故选D.
3. 【分析】根据圆周角定理、垂径定理知识,运用排除法,逐题分析判断.
解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;www.21-cn-jy.com
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选A.
4. 【分析】由切线的判定,结合角平分线的性质,即可证明.
解:连接NP.
∵⊙P与OC相切.
∴PN⊥OC.
即PN为圆半径,
作PM⊥OB.
又∵OA平分∠BOC,并由角平分线的性质.
∴PM=PN=圆半径.
∴⊙P与OB的位置关系为相切.
( http: / / www.21cnjy.com )
5.【分析】连接BE.根据两个圆的半径相等和圆周 ( http: / / www.21cnjy.com )角定理可以证明∠BAC=∠ABE,再结合三角形的外角的性质可以证明∠BEC=2∠BAC,从而肯定该圆一定过三角形的外心.
解:如图,连接BE.21*cnjy*com
因为△ABC为锐角三角形,所以∠BAC,∠ABE均为锐角.
又因为⊙O的半径与△ADE的外接圆的半径相等,且DE为两圆的公共弦,所以∠BAC=∠ABE.
于是,∠BEC=∠BAC+∠ABE=2∠BAC.
若△ABC的外心为O1,则∠BO1C=2∠BAC,
所以⊙O一定过△ABC的外心.
故选B.
6.【分析】连接OA,BO ( http: / / www.21cnjy.com ),由圆周角定理知可知∠AOB=2∠E=120°,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P=180°﹣∠AOB=60°.
解:连接OA,BO;
∵∠AOB=2∠E=120°,
∴∠OAP=∠OBP=90°,
∴∠P=180°﹣∠AOB=60°.
故选B.
( http: / / www.21cnjy.com )
7.【分析】由图可知AE=6,BE=4,根据切割线定理可求出BD为2,所以CD为6,⊙O半径为3.
解:∵AC,AE为⊙O的切线,
∴AC=AE=6,
根据勾股定理可知AB=10,
∴BE=4;
根据切割线定理有,
BE2=BD×BC可得,
BD=2,
∴CD=6,
∴⊙O半径为3.
故选C.
8. 【分析】根据角平分线上的点到这个角的两边的距离相等,所以三角形内切圆的圆心是三内角平分线的交点.【来源:21·世纪·教育·网】
解:∵角平分线上的点到角的两边的距离相等,
∴三角形内切圆的圆心是三内角平分线的交点.
故选B.
9.【分析】作DH⊥BC于H,如图,利用平行线的性质得AB⊥AD,AB⊥BC,则根据切线的判定得到AD和BC为⊙O切线,根据切线长定理得DE=DA=2,CE=CB,NE=NF,MB=MF,利用四边形ABHD为矩形得BH=AD=2,DH=AB=6,设BC=x,则CH=x﹣2,CD=x+2,在Rt△DCH中根据勾股定理得(x﹣2)2+62=(x+2)2,解得x= ( http: / / www.21cnjy.com ),即CB=CE= ( http: / / www.21cnjy.com ),然后由等线段代换得到△MCN的周长=CE+CB=9.2-1-c-n-j-y
解:作DH⊥BC于H,如图,
∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O 切线,
∵CD和MN为⊙O 切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x﹣2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x﹣2)2+62=(x+2)2,解得x= ( http: / / www.21cnjy.com ),
∴CB=CE= ( http: / / www.21cnjy.com ),
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
( http: / / www.21cnjy.com )
10. 【分析】连结OA、OB,根据切线的性质和l1∥l2得到AB为⊙O的直径,则l1和l2的距离为2;当MN与⊙O相切,连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO=∠AMN=30°,在Rt△AMO中,利用正切的定义可计算出AM= ( http: / / www.21cnjy.com ),在Rt△OBN中,由于∠ONB=∠BNM=60°,可计算出BN= ( http: / / www.21cnjy.com ),当MN在AB右侧时,AM= ( http: / / www.21cnjy.com ),所以AM的长为 ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com );当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,易证得Rt△OAF≌Rt△OBN,则OF=ON,于是可判断MO垂直平分NF,所以OM平分∠NMF,根据角平分线的性质得OE=OA,然后根据切线的判定定理得到MN为⊙O的切线.
解:连结OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;
作NH⊥AM于H,如图1,
则MN=AB=2,
∵∠AMN=60°,
∴sin60°= ( http: / / www.21cnjy.com ),
∴MN= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
当MN与⊙O相切,如图2,连结OM,ON,
当MN在AB左侧时,∠AMO= ( http: / / www.21cnjy.com )∠AMN= ( http: / / www.21cnjy.com )×60°=30°,
在Rt△AMO中,tan∠AMO= ( http: / / www.21cnjy.com ),即AM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△OBN中,∠ONB=∠BNM=60°,tan∠ONB= ( http: / / www.21cnjy.com ),即BN= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
当MN在AB右侧时,AM= ( http: / / www.21cnjy.com ),
∴AM的长为 ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com );
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.
故选B.
( http: / / www.21cnjy.com )
二.填空题(共6小题)
11.【分析】根据切割线定理即可求得PC的长,在直角△BCD中,利用勾股定理即可求解.
解:∵PA PB=PC PD,得8×18=PC (PC+7),
解得:PC=9,
连接BC,
∵PB=2PC,∠P=60°,
∴∠BCP=90°,
∴∠BCD=90°,
连接BD,
∵∠BCD=90°,
∴BD为直径,
BD===2.
故⊙O的半径为:.
12.【分析】辅助线,连 ( http: / / www.21cnjy.com )接OC与OE.根据一条弧所对的圆周角等于它所对的圆心角的一半,可知∠EOC的度数;再根据切线的性质定理,圆的切线垂直于经过切点的半径,可知OC⊥AB;又EF∥AB,可知OC⊥EF,最后由三角函数和垂径定理可将EF的长求出.
解:连接OE和OC,且OC与EF的交点为M.
∵∠EDC=30°,
∴∠COE=60°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin60°×OE= ( http: / / www.21cnjy.com )×2= ( http: / / www.21cnjy.com ),
∵EF=2EM,
∴EF= ( http: / / www.21cnjy.com ).
故答案为:2 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
13.【分析】当BC与⊙A相切,点A到BC的距离等于半径即可.
解:如图,过点A作AD⊥BC于点D.
∵AB=AC,∠B=30°,
∴AD= ( http: / / www.21cnjy.com )AB,即AB=2AD.
又∵BC与⊙A相切,
∴AD就是圆A的半径,
∴AD=3cm,
则AB=2AD=6cm.
故答案是:6.
( http: / / www.21cnjy.com )
14.【分析】根据弦切角等于弦切角所夹的弧所对的圆周角求出∠A=∠PCB,再根据直径所对的圆周角是直角得出∠A与∠B互余,计算即可求解.【出处:21教育名师】
解:∵PC切⊙O于点C,∠PCB=35°,
∴∠A=∠PCB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∴35°+∠B=90°,
解得∠B=55°.
故答案为:55.
15.【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.【版权所有:21教育】
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故答案为:2.
16.【分析】过点A作AM⊥BD与点M ( http: / / www.21cnjy.com ),在直角△AMD中,AD就可以利用AB表示出来,然后依据切割线定理,即可得到一个关于AB的方程,即可求解.
解:
过点A作AM⊥BD与点M.
∵AB为圆O的切线
∴∠ABD=∠C=45°(弦切角等于所夹弧所对的圆周角)
∵∠BDA=60°
∴∠BAD=75°,∠DAM=30°,∠BAM=45°
设AB=x,则AM= ( http: / / www.21cnjy.com )x,在直角△AMD中,AD= ( http: / / www.21cnjy.com )x
由切割线定理得:AB2=AD AC
x2= ( http: / / www.21cnjy.com )x( ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com ))
解得:x1=6,x2=0(舍去)
故AB=6.
故答案是:6.
( http: / / www.21cnjy.com )
三.解答题(共8小题)
17.【分析】根据直线和圆的位置关系得出d=r,根据根与系数的关系得出△=0,代入求出即可.
解:∵⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切,
∴d=r,
∵d,r是一元二次方程(m+9)x2﹣(m+6)x+1=0的两根,
∴△=0,
即[﹣(m+6)]2﹣4(m+9) 1=0,
解得:m=0或﹣8,
当m=﹣8时,x=﹣1,不符合题意舍去,
故m=0.
18.【分析】连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,根据切线性质得出AB=AM=R,求出CM=R﹣ ( http: / / www.21cnjy.com ),AC= ( http: / / www.21cnjy.com ),MN=2CM,2·1·c·n·j·y
由勾股定理得出方程R2=(R﹣ ( http: / / www.21cnjy.com ))2+( ( http: / / www.21cnjy.com ))2,求出方程的解即可.
解: ( http: / / www.21cnjy.com )
连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,
∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点 ( http: / / www.21cnjy.com ),与x轴相交于M、N两点,点M的坐标为 ( http: / / www.21cnjy.com ),
∴AB=AM=R,CM=R﹣ ( http: / / www.21cnjy.com ),AC= ( http: / / www.21cnjy.com ),MN=2CM,
由勾股定理得:R2=(R﹣ ( http: / / www.21cnjy.com ))2+( ( http: / / www.21cnjy.com ))2,
R=2.5,
∴CM=CN=2.5﹣ ( http: / / www.21cnjy.com )=2,
∴ON= ( http: / / www.21cnjy.com )+2+2=4 ( http: / / www.21cnjy.com ),
即N的坐标是(4 ( http: / / www.21cnjy.com ),0).
19.【分析】连接OD,可得OB=OD ( http: / / www.21cnjy.com ),由AB=AD,得到AE垂直平分BD,在直角三角形BOE中,利用锐角三角函数定义求出OE的长,根据勾股定理求出BE的长,由OC﹣OE求出CE的长,再利用勾股定理求出BC的长,利用勾股定理逆定理判断得到BC与OB垂直,即可确定出BC为圆O的切线.
证明:连接OD,可得OB=OD,
∵AB=AD,
∴AE垂直平分BD,
在Rt△BOE中,OB=3,cos∠BOE= ( http: / / www.21cnjy.com ),
∴OE= ( http: / / www.21cnjy.com ),
根据勾股定理得:BE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),CE=OC﹣OE= ( http: / / www.21cnjy.com ),
在Rt△CEB中,BC= ( http: / / www.21cnjy.com )=4,
∵OB=3,BC=4,OC=5,
∴OB2+BC2=OC2,
∴∠OBC=90°,即BC⊥OB,
则BC为圆O的切线.
( http: / / www.21cnjy.com )
20.【分析】连接AE,利用等腰三角形的性质易证∠BAE=∠CAE= ( http: / / www.21cnjy.com )∠CAB,由弦切角定理可得∠CBD=∠BAE,所以∠CBD= ( http: / / www.21cnjy.com )∠CAB.21*cnjy*com
证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE= ( http: / / www.21cnjy.com )∠CAB,
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD= ( http: / / www.21cnjy.com )∠CAB.
( http: / / www.21cnjy.com )
21.【分析】由切线长定理知,AE=CE,FB=CF,PA=PB=12,然后根据△PEF的周长公式即可求出其结果
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
22.【分析】连接PO交AB于H,设DE=x,由勾股定理得,(x+2)2+x=2(x+3),从而求出x的值即可.
解:连接PO交AB于H,由切线长定理可知,OP平分∠APB,而PA=PB,
( http: / / www.21cnjy.com )
∴PO⊥AB,
设DE=x,则PA2=PE PC=2(x+3).
在Rt△APH中,AP2=AH2+PH2,即AH2+PH2=2(x+3)①,
在Rt△PHD中,PH2+DH2=(x+2)2②,
又AD DB=ED DC,而AD DB=(AH﹣DH)(AH+DH)=AH2﹣DH2,
∴AH2﹣DH2=x 1③,
由①②③得(x+2)2+x=2(x+3),
解得DE=x= ( http: / / www.21cnjy.com ).
23.【分析】(1)利用切线长定理得出AD=AF,BD=BE,CE=CF,进而得出BD=CF,即可得出答案;21·cn·jy·com
(2)首先连结OD、OE,进而利用 ( http: / / www.21cnjy.com )切线的性质得出∠ODA=∠OFA=∠A=90°,进而得出四边形ODAF是正方形,再利用勾股定理求出⊙O的半径.
解法一:(1)证明:∵⊙O是△ABC的内切圆,切点为D、E、F
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,
∴AB﹣AD=AC﹣AF,
即BD=CF,
∴BE=CE;
解法二:(1)证明:连结OB、OC、OE
∵⊙O是△ABC的内切圆,
∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC= ( http: / / www.21cnjy.com )∠ABC,∠OCB= ( http: / / www.21cnjy.com )∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
又∵⊙O是△ABC的内切圆,切点为E,
∴OE⊥BC,
∴BE=CE;
(2)解:连结OD、OE,
∵⊙O是△ABC的内切圆,切点为D、E、F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,
∴四边形ODAF是正方形,
设OD=AD=AF=r,
则BE=BD=CF=CE=2﹣r,
在△ABC中,∠A=90°,
∴ ( http: / / www.21cnjy.com ),
又∵BC=BE+CE,
∴(2﹣r)+(2﹣r)= ( http: / / www.21cnjy.com ),
得:r= ( http: / / www.21cnjy.com ),
∴⊙O的半径是 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
24.【分析】(1)根据内心性质得∠1= ( http: / / www.21cnjy.com )∠2,∠3=∠4,则AD=CD,于是可判断四边形OADC为菱形,则BD垂直平分AC,∠4=∠5=∠6,易得OA=OC,∠2=∠3,所以OB=OC,可判断点O为△ABC的外心,则可判断△ABC为等边三角形,所以∠AOB=∠BOC=∠AOC=120°,BC=AC,再根据平行四边形的性质得∠ADC=∠AOC=120°,AD=OC,CD=OA=OB,则根据“SAS”证明△BOC≌△CDA;【来源:21cnj*y.co*m】
(2)作OH⊥AB于H,如图,根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°,根据垂径定理得到BH=AH= ( http: / / www.21cnjy.com )AB=1,再利用含30度的直角三角形三边的关系得到BH=AH= ( http: / / www.21cnjy.com )AB=1,OH= ( http: / / www.21cnjy.com )BH= ( http: / / www.21cnjy.com ),OB=2OH= ( http: / / www.21cnjy.com ),然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB﹣S△AOB进行计算即可.21教育名师原创作品
(1)证明:∵O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
( http: / / www.21cnjy.com ),
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠OBH= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,
∵OH⊥AB,
∴BH=AH= ( http: / / www.21cnjy.com )AB=1,
OH= ( http: / / www.21cnjy.com )BH= ( http: / / www.21cnjy.com ),
OB=2OH= ( http: / / www.21cnjy.com ),
∴S阴影部分=S扇形AOB﹣S△AOB
= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2× ( http: / / www.21cnjy.com )
= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
直线和园的位置关系单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共10小题)
1.已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点共有( )21cnjy.com
A.1个 B.2个 C.3个 D.4个
2.已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么( )
A.0<OP<5 B.OP=5 C.OP>5 D.OP≥5
3.有下列结论:(1)平分弦的直径垂直于 ( http: / / www.21cnjy.com )弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
4.已知OA平分∠BOC,P是OA上一点,以P为圆心的⊙P与OC相切,则⊙P与OB的位置关系为( )
A.相离 B.相切 C.相交 D.不能确定
5.已知△ABC为锐角三角形,⊙O经过点B ( http: / / www.21cnjy.com ),C,且与边AB,AC分别相交于点D,E.若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的( )
A.内心 B.外心 C.重心 D.垂心
6.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
( http: / / www.21cnjy.com )
A.120° B.60° C.30° D.45°
7.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,CD为直径的⊙O与AB相切于E,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A.2 B.2.5 C.3 D.4
8.三角形内切圆的圆心为( )
A.三条边的高的交点 B.三个角的平分线的交点
C.三条边的垂直平分线的交点 D.三条边的中线的交点
9.如图,四边形ABCD中,AD平行BC, ( http: / / www.21cnjy.com )∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
( http: / / www.21cnjy.com )
A.9 B.10 C.3 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
10.如图,直线l1∥l2 ( http: / / www.21cnjy.com ),⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )
( http: / / www.21cnjy.com )
A.l1和l2的距离为2 B.当MN与⊙O相切时,AM= ( http: / / www.21cnjy.com )
C.MN= ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) D.当∠MON=90°时,MN与⊙O相切
二.填空题(共6小题)
11.已知PAB、PCD为⊙O的两条割线,PA=8,AB=10,CD=7,∠P=60°,则⊙O的半径为 .
12.如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
13.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB= cm时,BC与⊙A相切.
( http: / / www.21cnjy.com )
14.如图,已知AB是⊙O的直径,PC切⊙O于点C,∠PCB=35°,则∠B等于 度.
( http: / / www.21cnjy.com )
15.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
( http: / / www.21cnjy.com )
16.如图,AB,AC分别是⊙O的切线和割线,且∠C=45°,∠BDA=60°,CD= ( http: / / www.21cnjy.com ),则切线AB的长是 .
( http: / / www.21cnjy.com )
三.解答题(共8小题)
17.设⊙O的圆心O到直线的距离为d, ( http: / / www.21cnjy.com )半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2﹣(m+6)x+1=0的两根,求m的值.
18.如图,在平面直角坐标系xOy中,⊙A与y轴相切于点 ( http: / / www.21cnjy.com ),与x轴相交于M、N两点.如果点M的坐标为 ( http: / / www.21cnjy.com ),求点N的坐标.
( http: / / www.21cnjy.com )
19.如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE= ( http: / / www.21cnjy.com ).求证:CB是⊙O的切线.
( http: / / www.21cnjy.com )
20.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD= ( http: / / www.21cnjy.com )∠CAB.
( http: / / www.21cnjy.com )
21.如图示,PA,PB分别与⊙O ( http: / / www.21cnjy.com )相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
( http: / / www.21cnjy.com )
22.如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.
( http: / / www.21cnjy.com )
23.如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
( http: / / www.21cnjy.com )
24.如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共10小题)
1. 【分析】根据平行线间的距离相等,先过点D作AB⊥OC,即可求得⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点的个数.21世纪教育网版权所有
解:如图,
∵⊙O的半径为5,点O到直线l的距离为3,
∴CE=2,
过点D作AB⊥OC,垂足为D,交⊙O于A、B两点,且DE= ( http: / / www.21cnjy.com ),
∴⊙O上到直线l的距离为 ( http: / / www.21cnjy.com )的点在直线l的左边和右边各有两个,共四个,
故选D.
( http: / / www.21cnjy.com )
2.【分析】由⊙O的半径是5,直线 ( http: / / www.21cnjy.com )l是⊙O的切线,P是l上的任一点,可得当P与切点重合时,OP=5,当P与切点不重合时,OP>5,继而求得答案.21教育网
解:∵⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,
∴当P与切点重合时,OP=5,
当P与切点不重合时,OP>5,
∴OP≥5.
故选D.
3. 【分析】根据圆周角定理、垂径定理知识,运用排除法,逐题分析判断.
解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;www.21-cn-jy.com
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选A.
4. 【分析】由切线的判定,结合角平分线的性质,即可证明.
解:连接NP.
∵⊙P与OC相切.
∴PN⊥OC.
即PN为圆半径,
作PM⊥OB.
又∵OA平分∠BOC,并由角平分线的性质.
∴PM=PN=圆半径.
∴⊙P与OB的位置关系为相切.
( http: / / www.21cnjy.com )
5.【分析】连接BE.根据两个圆的半径相等和圆周 ( http: / / www.21cnjy.com )角定理可以证明∠BAC=∠ABE,再结合三角形的外角的性质可以证明∠BEC=2∠BAC,从而肯定该圆一定过三角形的外心.
解:如图,连接BE.21*cnjy*com
因为△ABC为锐角三角形,所以∠BAC,∠ABE均为锐角.
又因为⊙O的半径与△ADE的外接圆的半径相等,且DE为两圆的公共弦,所以∠BAC=∠ABE.
于是,∠BEC=∠BAC+∠ABE=2∠BAC.
若△ABC的外心为O1,则∠BO1C=2∠BAC,
所以⊙O一定过△ABC的外心.
故选B.
6.【分析】连接OA,BO ( http: / / www.21cnjy.com ),由圆周角定理知可知∠AOB=2∠E=120°,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P=180°﹣∠AOB=60°.
解:连接OA,BO;
∵∠AOB=2∠E=120°,
∴∠OAP=∠OBP=90°,
∴∠P=180°﹣∠AOB=60°.
故选B.
( http: / / www.21cnjy.com )
7.【分析】由图可知AE=6,BE=4,根据切割线定理可求出BD为2,所以CD为6,⊙O半径为3.
解:∵AC,AE为⊙O的切线,
∴AC=AE=6,
根据勾股定理可知AB=10,
∴BE=4;
根据切割线定理有,
BE2=BD×BC可得,
BD=2,
∴CD=6,
∴⊙O半径为3.
故选C.
8. 【分析】根据角平分线上的点到这个角的两边的距离相等,所以三角形内切圆的圆心是三内角平分线的交点.【来源:21·世纪·教育·网】
解:∵角平分线上的点到角的两边的距离相等,
∴三角形内切圆的圆心是三内角平分线的交点.
故选B.
9.【分析】作DH⊥BC于H,如图,利用平行线的性质得AB⊥AD,AB⊥BC,则根据切线的判定得到AD和BC为⊙O切线,根据切线长定理得DE=DA=2,CE=CB,NE=NF,MB=MF,利用四边形ABHD为矩形得BH=AD=2,DH=AB=6,设BC=x,则CH=x﹣2,CD=x+2,在Rt△DCH中根据勾股定理得(x﹣2)2+62=(x+2)2,解得x= ( http: / / www.21cnjy.com ),即CB=CE= ( http: / / www.21cnjy.com ),然后由等线段代换得到△MCN的周长=CE+CB=9.2-1-c-n-j-y
解:作DH⊥BC于H,如图,
∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O 切线,
∵CD和MN为⊙O 切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x﹣2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x﹣2)2+62=(x+2)2,解得x= ( http: / / www.21cnjy.com ),
∴CB=CE= ( http: / / www.21cnjy.com ),
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
( http: / / www.21cnjy.com )
10. 【分析】连结OA、OB,根据切线的性质和l1∥l2得到AB为⊙O的直径,则l1和l2的距离为2;当MN与⊙O相切,连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO=∠AMN=30°,在Rt△AMO中,利用正切的定义可计算出AM= ( http: / / www.21cnjy.com ),在Rt△OBN中,由于∠ONB=∠BNM=60°,可计算出BN= ( http: / / www.21cnjy.com ),当MN在AB右侧时,AM= ( http: / / www.21cnjy.com ),所以AM的长为 ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com );当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,易证得Rt△OAF≌Rt△OBN,则OF=ON,于是可判断MO垂直平分NF,所以OM平分∠NMF,根据角平分线的性质得OE=OA,然后根据切线的判定定理得到MN为⊙O的切线.
解:连结OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;
作NH⊥AM于H,如图1,
则MN=AB=2,
∵∠AMN=60°,
∴sin60°= ( http: / / www.21cnjy.com ),
∴MN= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
当MN与⊙O相切,如图2,连结OM,ON,
当MN在AB左侧时,∠AMO= ( http: / / www.21cnjy.com )∠AMN= ( http: / / www.21cnjy.com )×60°=30°,
在Rt△AMO中,tan∠AMO= ( http: / / www.21cnjy.com ),即AM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△OBN中,∠ONB=∠BNM=60°,tan∠ONB= ( http: / / www.21cnjy.com ),即BN= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
当MN在AB右侧时,AM= ( http: / / www.21cnjy.com ),
∴AM的长为 ( http: / / www.21cnjy.com )或 ( http: / / www.21cnjy.com );
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.
故选B.
( http: / / www.21cnjy.com )
二.填空题(共6小题)
11.【分析】根据切割线定理即可求得PC的长,在直角△BCD中,利用勾股定理即可求解.
解:∵PA PB=PC PD,得8×18=PC (PC+7),
解得:PC=9,
连接BC,
∵PB=2PC,∠P=60°,
∴∠BCP=90°,
∴∠BCD=90°,
连接BD,
∵∠BCD=90°,
∴BD为直径,
BD===2.
故⊙O的半径为:.
12.【分析】辅助线,连 ( http: / / www.21cnjy.com )接OC与OE.根据一条弧所对的圆周角等于它所对的圆心角的一半,可知∠EOC的度数;再根据切线的性质定理,圆的切线垂直于经过切点的半径,可知OC⊥AB;又EF∥AB,可知OC⊥EF,最后由三角函数和垂径定理可将EF的长求出.
解:连接OE和OC,且OC与EF的交点为M.
∵∠EDC=30°,
∴∠COE=60°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin60°×OE= ( http: / / www.21cnjy.com )×2= ( http: / / www.21cnjy.com ),
∵EF=2EM,
∴EF= ( http: / / www.21cnjy.com ).
故答案为:2 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
13.【分析】当BC与⊙A相切,点A到BC的距离等于半径即可.
解:如图,过点A作AD⊥BC于点D.
∵AB=AC,∠B=30°,
∴AD= ( http: / / www.21cnjy.com )AB,即AB=2AD.
又∵BC与⊙A相切,
∴AD就是圆A的半径,
∴AD=3cm,
则AB=2AD=6cm.
故答案是:6.
( http: / / www.21cnjy.com )
14.【分析】根据弦切角等于弦切角所夹的弧所对的圆周角求出∠A=∠PCB,再根据直径所对的圆周角是直角得出∠A与∠B互余,计算即可求解.【出处:21教育名师】
解:∵PC切⊙O于点C,∠PCB=35°,
∴∠A=∠PCB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∴35°+∠B=90°,
解得∠B=55°.
故答案为:55.
15.【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.【版权所有:21教育】
解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故答案为:2.
16.【分析】过点A作AM⊥BD与点M ( http: / / www.21cnjy.com ),在直角△AMD中,AD就可以利用AB表示出来,然后依据切割线定理,即可得到一个关于AB的方程,即可求解.
解:
过点A作AM⊥BD与点M.
∵AB为圆O的切线
∴∠ABD=∠C=45°(弦切角等于所夹弧所对的圆周角)
∵∠BDA=60°
∴∠BAD=75°,∠DAM=30°,∠BAM=45°
设AB=x,则AM= ( http: / / www.21cnjy.com )x,在直角△AMD中,AD= ( http: / / www.21cnjy.com )x
由切割线定理得:AB2=AD AC
x2= ( http: / / www.21cnjy.com )x( ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com ))
解得:x1=6,x2=0(舍去)
故AB=6.
故答案是:6.
( http: / / www.21cnjy.com )
三.解答题(共8小题)
17.【分析】根据直线和圆的位置关系得出d=r,根据根与系数的关系得出△=0,代入求出即可.
解:∵⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切,
∴d=r,
∵d,r是一元二次方程(m+9)x2﹣(m+6)x+1=0的两根,
∴△=0,
即[﹣(m+6)]2﹣4(m+9) 1=0,
解得:m=0或﹣8,
当m=﹣8时,x=﹣1,不符合题意舍去,
故m=0.
18.【分析】连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,根据切线性质得出AB=AM=R,求出CM=R﹣ ( http: / / www.21cnjy.com ),AC= ( http: / / www.21cnjy.com ),MN=2CM,2·1·c·n·j·y
由勾股定理得出方程R2=(R﹣ ( http: / / www.21cnjy.com ))2+( ( http: / / www.21cnjy.com ))2,求出方程的解即可.
解: ( http: / / www.21cnjy.com )
连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,
∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点 ( http: / / www.21cnjy.com ),与x轴相交于M、N两点,点M的坐标为 ( http: / / www.21cnjy.com ),
∴AB=AM=R,CM=R﹣ ( http: / / www.21cnjy.com ),AC= ( http: / / www.21cnjy.com ),MN=2CM,
由勾股定理得:R2=(R﹣ ( http: / / www.21cnjy.com ))2+( ( http: / / www.21cnjy.com ))2,
R=2.5,
∴CM=CN=2.5﹣ ( http: / / www.21cnjy.com )=2,
∴ON= ( http: / / www.21cnjy.com )+2+2=4 ( http: / / www.21cnjy.com ),
即N的坐标是(4 ( http: / / www.21cnjy.com ),0).
19.【分析】连接OD,可得OB=OD ( http: / / www.21cnjy.com ),由AB=AD,得到AE垂直平分BD,在直角三角形BOE中,利用锐角三角函数定义求出OE的长,根据勾股定理求出BE的长,由OC﹣OE求出CE的长,再利用勾股定理求出BC的长,利用勾股定理逆定理判断得到BC与OB垂直,即可确定出BC为圆O的切线.
证明:连接OD,可得OB=OD,
∵AB=AD,
∴AE垂直平分BD,
在Rt△BOE中,OB=3,cos∠BOE= ( http: / / www.21cnjy.com ),
∴OE= ( http: / / www.21cnjy.com ),
根据勾股定理得:BE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),CE=OC﹣OE= ( http: / / www.21cnjy.com ),
在Rt△CEB中,BC= ( http: / / www.21cnjy.com )=4,
∵OB=3,BC=4,OC=5,
∴OB2+BC2=OC2,
∴∠OBC=90°,即BC⊥OB,
则BC为圆O的切线.
( http: / / www.21cnjy.com )
20.【分析】连接AE,利用等腰三角形的性质易证∠BAE=∠CAE= ( http: / / www.21cnjy.com )∠CAB,由弦切角定理可得∠CBD=∠BAE,所以∠CBD= ( http: / / www.21cnjy.com )∠CAB.21*cnjy*com
证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE= ( http: / / www.21cnjy.com )∠CAB,
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD= ( http: / / www.21cnjy.com )∠CAB.
( http: / / www.21cnjy.com )
21.【分析】由切线长定理知,AE=CE,FB=CF,PA=PB=12,然后根据△PEF的周长公式即可求出其结果
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
22.【分析】连接PO交AB于H,设DE=x,由勾股定理得,(x+2)2+x=2(x+3),从而求出x的值即可.
解:连接PO交AB于H,由切线长定理可知,OP平分∠APB,而PA=PB,
( http: / / www.21cnjy.com )
∴PO⊥AB,
设DE=x,则PA2=PE PC=2(x+3).
在Rt△APH中,AP2=AH2+PH2,即AH2+PH2=2(x+3)①,
在Rt△PHD中,PH2+DH2=(x+2)2②,
又AD DB=ED DC,而AD DB=(AH﹣DH)(AH+DH)=AH2﹣DH2,
∴AH2﹣DH2=x 1③,
由①②③得(x+2)2+x=2(x+3),
解得DE=x= ( http: / / www.21cnjy.com ).
23.【分析】(1)利用切线长定理得出AD=AF,BD=BE,CE=CF,进而得出BD=CF,即可得出答案;21·cn·jy·com
(2)首先连结OD、OE,进而利用 ( http: / / www.21cnjy.com )切线的性质得出∠ODA=∠OFA=∠A=90°,进而得出四边形ODAF是正方形,再利用勾股定理求出⊙O的半径.
解法一:(1)证明:∵⊙O是△ABC的内切圆,切点为D、E、F
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,
∴AB﹣AD=AC﹣AF,
即BD=CF,
∴BE=CE;
解法二:(1)证明:连结OB、OC、OE
∵⊙O是△ABC的内切圆,
∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC= ( http: / / www.21cnjy.com )∠ABC,∠OCB= ( http: / / www.21cnjy.com )∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
又∵⊙O是△ABC的内切圆,切点为E,
∴OE⊥BC,
∴BE=CE;
(2)解:连结OD、OE,
∵⊙O是△ABC的内切圆,切点为D、E、F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,
∴四边形ODAF是正方形,
设OD=AD=AF=r,
则BE=BD=CF=CE=2﹣r,
在△ABC中,∠A=90°,
∴ ( http: / / www.21cnjy.com ),
又∵BC=BE+CE,
∴(2﹣r)+(2﹣r)= ( http: / / www.21cnjy.com ),
得:r= ( http: / / www.21cnjy.com ),
∴⊙O的半径是 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
24.【分析】(1)根据内心性质得∠1= ( http: / / www.21cnjy.com )∠2,∠3=∠4,则AD=CD,于是可判断四边形OADC为菱形,则BD垂直平分AC,∠4=∠5=∠6,易得OA=OC,∠2=∠3,所以OB=OC,可判断点O为△ABC的外心,则可判断△ABC为等边三角形,所以∠AOB=∠BOC=∠AOC=120°,BC=AC,再根据平行四边形的性质得∠ADC=∠AOC=120°,AD=OC,CD=OA=OB,则根据“SAS”证明△BOC≌△CDA;【来源:21cnj*y.co*m】
(2)作OH⊥AB于H,如图,根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°,根据垂径定理得到BH=AH= ( http: / / www.21cnjy.com )AB=1,再利用含30度的直角三角形三边的关系得到BH=AH= ( http: / / www.21cnjy.com )AB=1,OH= ( http: / / www.21cnjy.com )BH= ( http: / / www.21cnjy.com ),OB=2OH= ( http: / / www.21cnjy.com ),然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB﹣S△AOB进行计算即可.21教育名师原创作品
(1)证明:∵O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
( http: / / www.21cnjy.com ),
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠OBH= ( http: / / www.21cnjy.com )(180°﹣120°)=30°,
∵OH⊥AB,
∴BH=AH= ( http: / / www.21cnjy.com )AB=1,
OH= ( http: / / www.21cnjy.com )BH= ( http: / / www.21cnjy.com ),
OB=2OH= ( http: / / www.21cnjy.com ),
∴S阴影部分=S扇形AOB﹣S△AOB
= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2× ( http: / / www.21cnjy.com )
= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
