第二章 直线与圆的位置关系单元检测B卷
文档属性
| 名称 | 第二章 直线与圆的位置关系单元检测B卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 514.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-20 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
直线与圆的位置关系单元检测B卷
姓名:__________班级:__________考号:__________
、选择题(本大题共10小题 )
已知⊙O的半径r=5,圆心O到直线l的距离为( )时,圆与直线l相交.
A. 7 B. 6 C. 5 D. 4
下列说法正确的是( )
A.与圆有公共点的直线是圆的切线
B.到圆心距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径外端的直线是圆的切线
如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径 C.AB是直径,B是切点 D.AB是直径,B是切点
已知⊙O的半径是5,直线是⊙O的切线,则点O到直线的距离是( )
A.2.5 B.3 C.5 D.10
已知如图,AB为半圆的直径,C、D为半圆弧上的两点,若弧CD=弧BD,DC与BA的延长线交于P,如果,AP:CP=3:4,△ADB的面积为,则AP的长为( )
A.7 B.12 C. D.4
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC,若∠A=36°,则∠C等于( )
A. 36° B. 54° C. 60° D. 27°
等腰三角形中,AB=AC,BC=4,△ABC的内切圆的半径为1,则AB的长为( )
A.2 B.3 C. D.
如图已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的圆O的切线交BC于点E,若CD=5,CE=4,则圆O的半径是( )
A.3 B.4 C. D.
Rt△ABC中,∠C=90°,AB=5,内切圆半径为1,则三角形的周长为( )
A.15 B.12 C.13 D.14
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A. B. C. D.
将正方形ABCD绕点A按逆时针方向旋转,得正方形,交CD于点E,AB=,则四边形的内切圆半径为( )
A. B. C. D.
、填空题(本大题共6小题 )
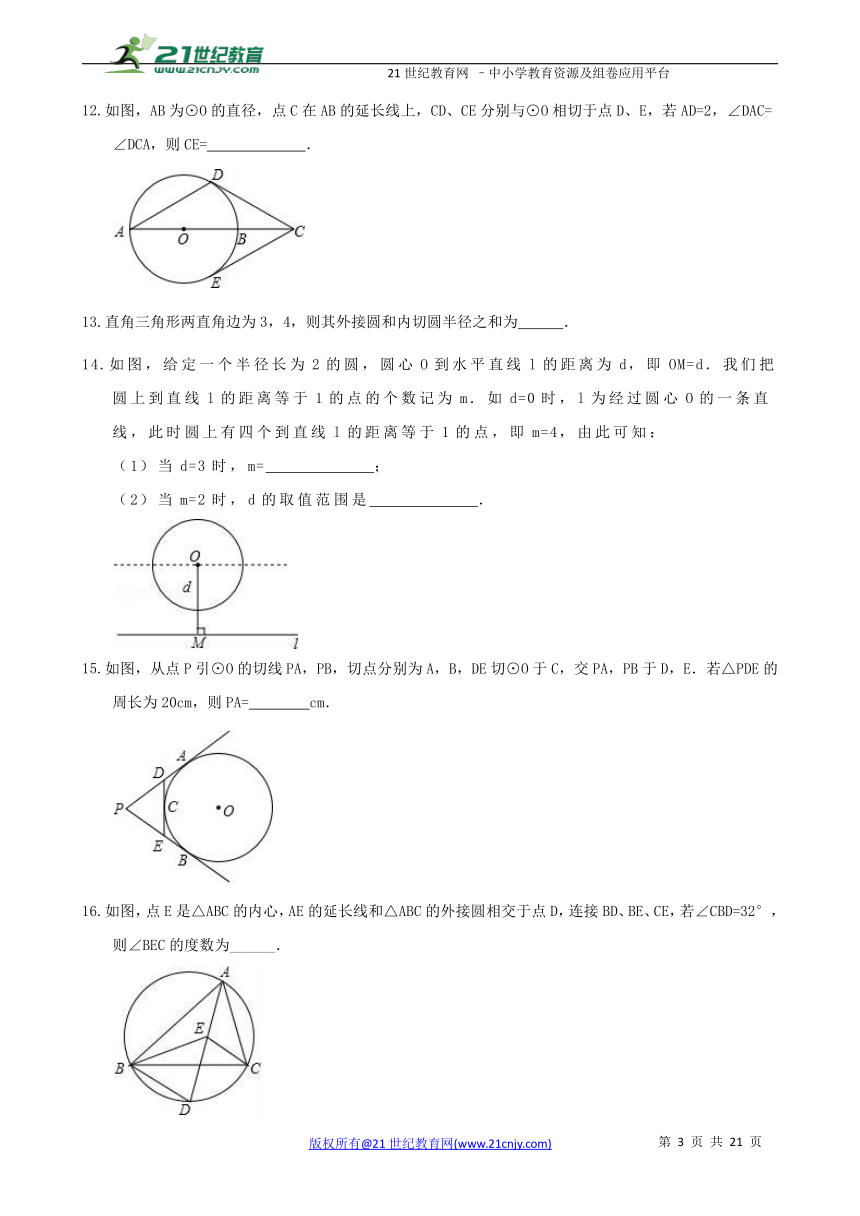
如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .
如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
如图,从点P引⊙O的切线PA,PB,切点分别为A,B,DE切⊙O于C,交PA,PB于D,E.若△PDE的周长为20cm,则PA= cm.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为______.
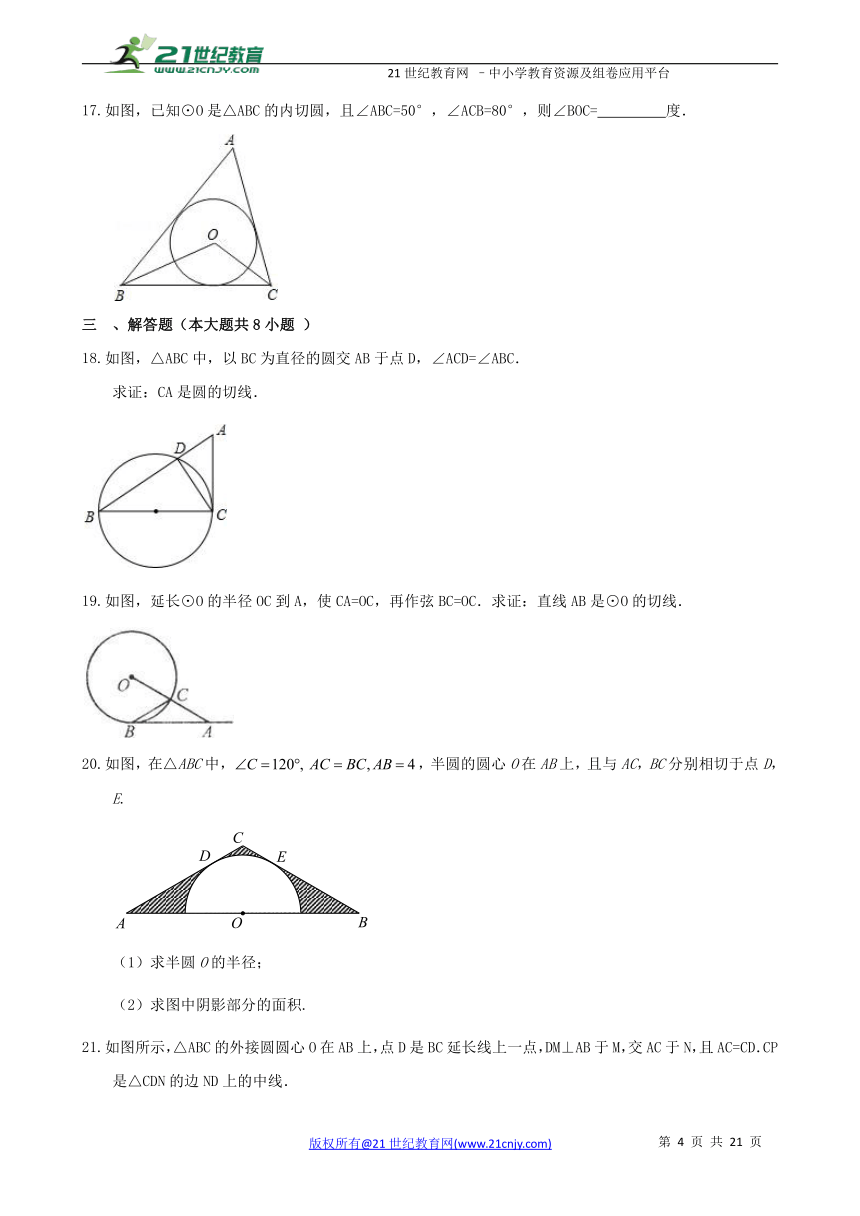
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
、解答题(本大题共8小题 )
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
求证:CA是圆的切线.
如图,延长⊙O的半径OC到A,使CA=OC,再作弦BC=OC.求证:直线AB是⊙O的切线.
如图,在△ABC中,,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E.
(1)求半圆O的半径;
(2)求图中阴影部分的面积.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
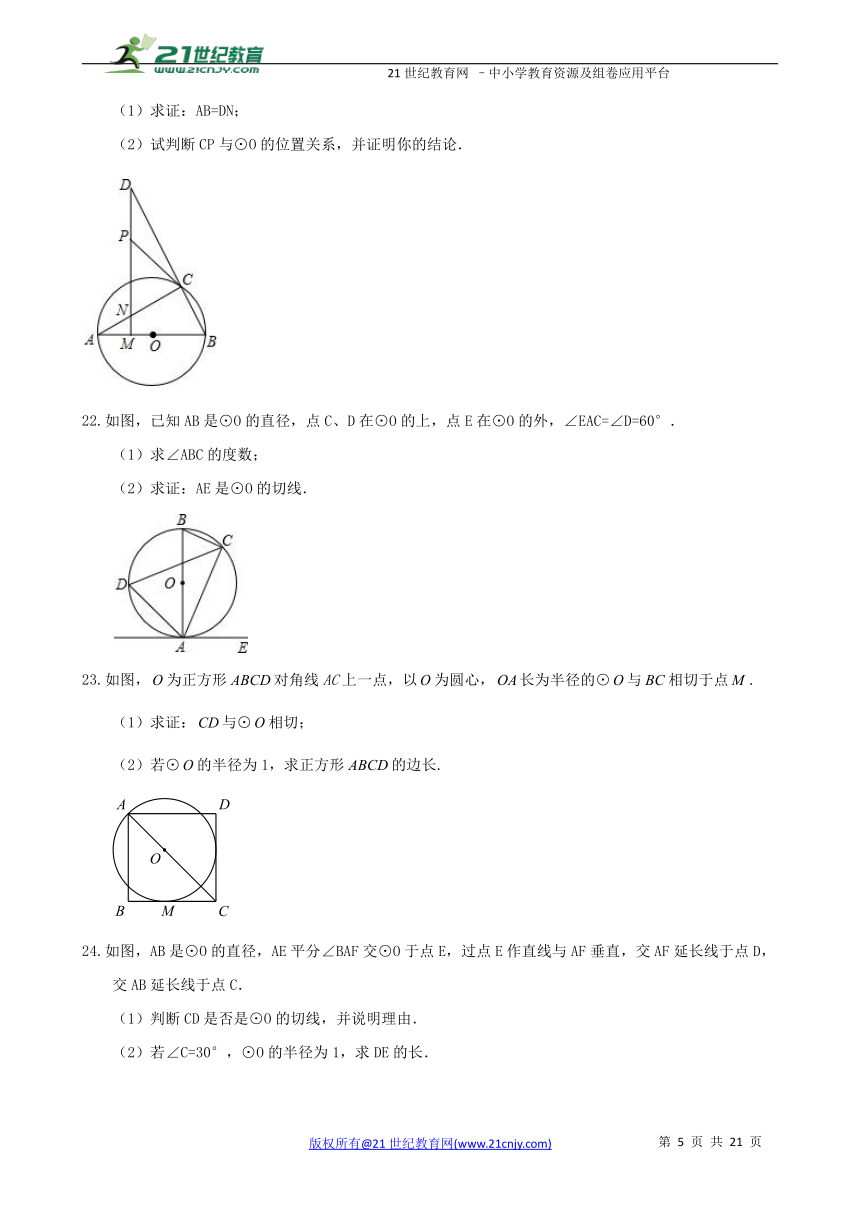
(1)求证:AB=DN;
(2)试判断CP与⊙O的位置关系,并证明你的结论.
如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线.
如图,为正方形对角线AC上一点,以为圆心,长为半径的⊙与相切于点.
(1)求证:与⊙相切;
(2)若⊙的半径为1,求正方形的边长.
如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF延长线于点D,交AB延长线于点C.
(1)判断CD是否是⊙O的切线,并说明理由.
(2)若∠C=30°,⊙O的半径为1,求DE的长.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
答案解析
、选择题
【分析】 直接根据直线和圆相交的条件即可得出结论.
解:∵⊙O的半径r=5,圆与直线l相交,
∴圆心O到直线l的距离d<5.
故选D.
【分析】根据切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.
解:A.与圆只有一个交点的直线是圆的切线,故本选项错误;
B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;
C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;
D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.
故选B.
【分析】根据圆的切线的判定方法“圆的切线垂直于经过切点的半径”,进行分析.
解:根据切线的判定方法,则这里的AB是直径,且一端是切点.
故选C.
【分析】根据直线与圆的位置关系可直接得到点O到直线l的距离如果⊙O的半径为r,圆心O到直线l的距离为d,那么直线l和⊙O相切 d=r;所以点O到直线的距离等于半径.
解:∵直线l与半径为r的⊙O相切,
∴点O到直线l的距离等于圆的半径,
即点O到直线l的距离为5.
故选C.
【分析】连OD、AC可以根据平行线分线段成比例定理的逆定理证明AC∥OD,则CD即可利用圆的半径表示出来,进而表示出BD,在直角△ABD中利用勾股定理即可求得AD,再根据△ADB的面积为可以得到关于半径的方程求得圆的半径,利用切割线定理即可求解.
解:设AO=R,连OD、AC.
∵=
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴AC∥OD,
∴==,
∴CD=R,
∴BD=R,
∴AD===R,
由S△AOB=16,
得: =16,
∴R=6,
∵PA PB=PC PD,设PA=x,则x(x+12)=x(x+8),
∴x=.
故PA=.
故选C.
【分析】根据题目条件易求∠BOA,根据圆周角定理求出∠C=∠BOA,即可求出答案.
∵AB与⊙O相切于点B,
∴∠ABO=90°,
∵∠A=36°,
∴∠BOA=54°,
∴由圆周角定理得:∠C=∠BOA=27°,
故选D.
【分析】利用三角形内切圆的性质以及切线长定理得出BD=BE,CE=CF,AD=AF,进而得出△ADF是等边三角形,即可得出答案.
解:∵△ABC的内切圆O与三边分别切于D、E、F,CB=6cm,△ABC的周长为16cm,
∴BD=BE,CE=CF,AD=AF,
∵BE+EC=BD+FC=6,
∴AD=AF=(AB+AC+BC-BC-BD-CF)=(16-6-6)=2,
∵∠A=60°,
∴△ADF是等边三角形,
∴DF=2.
故选:A.
解:连接OD,DB
【分析】根据切线的性质得出∠ODC=∠OFC=∠ACB=90°,得出正方形ODCF,求出CD=CF=1,根据切线长定理求出AD+BF=AE+BE=5,代入AC+BC+AB求出即可.
解:连接OA.OB、OC、OD、OE、OF,
∵⊙O是△ABC的内切圆,切点分别是D、E、F,
∴OD⊥AC,OE⊥AB,OF⊥BC,AD=AE,BE=BF,
∴∠ODC=∠OFC=∠ACB=90°,
∵OD=OF,
∴四边形ODCF是正方形,
∴CD=OD=OF=CF=1,
∵AD=AE,BF=BE,
∵AE+BE=AB=5,
∴AD+BF=5,
∴△ABC的周长是:AC+BC+AB=AD+CD+CF+BF+AB=5+1+1+5=12.
故选B.
【分析】过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解
解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=
∴CD=2,
∴图中阴影部分的面积为:-=
故选:A
解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
则∠OAF=30°,∠AB1O=45°,
故B1F=OF=OA,
设B1F=x,则AF=﹣x,
故(﹣x)2+x2=(2x)2,
解得x=或x=(舍去),
∴四边形AB1ED的内切圆半径为:.
故选:B.
、填空题
【分析】有条件可得AD=CD,再有切线长定理可得:CD=CE,所以AD=CE,问题的解.
解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
【分析】首先根据勾股定理求得该直角三角形的斜边是5,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解:∵直角三角形两直角边为3,4,
∴斜边长==5,
∴外接圆半径==2.5,内切圆半径==1,
∴外接圆和内切圆半径之和=2.5+1=3.5.
故答案为:3.5.
【分析】根据直线与圆的位置关系和直线与圆的交点个数以及命题中的数据分析即可得到答案.
解:(1)当d=3时,
∵3>2,即d>r,
∴直线与圆相离,则m=1,
故答案为:1;
(2)当m=2时,则圆上到直线l的距离等于1的点的个数记为2,
∴直线与圆相交或相切或相离,
∴0<d<3,
∴d的取值范围是0<d<3,
故答案为:0<d<3.
【分析】连接AO并延长交BC于D点,过点O作OE⊥AB于E,得到△AOE∽△ABD,再根据相似三角形对应边的比等于相似比进行计算求出AB边的长.
解:如图:
连接AO并延长交BC于点D,因为△ABC是等腰三角形,⊙O是△ABC的内切圆,
所以AD垂直平分BC,BD=CD=2,点O作OE⊥AB于E,
则点E是AB与⊙O的切点,由切线长定理得:BE=BD=2,
∴∠AEO=∠ADB=90°,∠OAE=∠BAD,
∴△AEO∽△ADB
∴=
∴=
解得:AE=,
∴AB=+2=.
故选D.
【分析】根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=÷2=58°,
∴∠BEC=180°﹣58°=122°.
故答案为:122°.
【分析】由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线;再利用角平分线的定义可知∠OBC+∠OCB=(∠ABC+∠ACB),代入数值即可求∠BOC=115°.
解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°﹣65°=115°.
、解答题
【分析】由BC为圆的直径,利用直径所对的圆周角为直角,得到△BDC为直角三角形,利用直角三角形的两锐角互余得到一对角互余,再由已知的角相等,等量代换可得出AC与BC垂直,进而确定出CA为圆的切线.
证明:∵BC为圆的直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
又∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,即∠ACB=90°,
∴AC⊥BC,BC为圆的直径,
∴CA为圆的切线.
【分析】连OB,要直线AB是⊙O的切线,即证明OB⊥BA即可.由BC=OC,CA=OC,即BC=CA=CB,则得到△OBA为直角三角形,所以有OB⊥BA.
证明:连OB,如图,
∵BC=OC,CA=OC,
∴BC为△OBA的中线,且BC=OA,
∴△OBA为直角三角形,
即OB⊥BA.
所以直线AB是⊙O的切线.
(1)解:连结OD,OC,
∵半圆与AC,BC分别相切于点D,E.
∴,且.
∵,
∴且O是AB的中点.
∴.
∵,∴.
∴.
∴在中,.
即半圆的半径为1.
【分析】(1)根据圆周角定理得到∴∠ACB=90°,则∠NCD=90°,而DM⊥AB,根据等角的余角相等得到∠A=∠D,然后根据“ASA”判断△ABC≌△DNC,则AB=DN;
(2)根据直角三角形斜边上的中线性质得PC=PN=,则∠PCN=∠PNC,所以∠ANM=∠PCN,而∠A=∠ACO,于是得到∠ACO+∠PCN=90°,
即∠PCO=90°,然后根据切线的判定定理得到CP是⊙O的切线.
(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,则∠NCD=90°,
∵DM⊥AB,
∴∠AMN=90°,
∴∠ABC+∠A=∠ABC+∠D=90°,
∴∠A=∠D,
在△ABC和△DNC中
,
∴△ABC≌△DNC(ASA),
∴AB=DN;
(2)CP是⊙O的切线.理由如下:
连结OC,如图,
∵CP是△CDN的边ND上的中线,∠NCD=90°,
∴PC=PN=,
∴∠PCN=∠PNC,
∵∠ANM=∠PNC,
∴∠ANM=∠PCN,
∵OA=OC,
∴∠A=∠ACO,
∵∠A+∠ANM=90°,
∴∠ACO+∠PCN=90°,
∴∠PCO=90°,
∴OC⊥PC
∴CP是⊙O的切线.
【分析】直接根据圆周角定理求解;
(2)根据圆周角定理,由AB是⊙O的直径得∠ACB=90°,则利用互余可计算出∠BAC=30°,于是得到∠BAE=∠BAC+∠EA=90°,然后根据切线的判定定理得到结论.
(1)解:∵∠D=60°,
∴∠ABC=∠D=60°;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣60°=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
∴BA⊥AE,
∴AE是⊙O的切线.
(1)证明:连接OM,过点O作ON⊥CD,垂足为N,
∵⊙0与BC相切于M,
∴OM⊥BC,
∵正方形ABCD中,AC平分∠BCD,
又∵ON⊥CD,OM⊥BC
∴OM=ON
∴CD与⊙O相切
(2)由(1)易知为等腰直角三角形,OM为半径,
∴ OM=MC=1.
∴ ,
∴
∴
在中,AB=BC,
有
∴
∴ .
故正方形的边长为.
【分析】(1)先证OE∥AD,得出∠ADC=∠OEC,再由AD⊥CD,证出OE⊥CD,即可得出结论;
(2)由∠C=30°,得出OC=2OE=2,AC=3,再根据含30°的直角三角形的性质求出AD,然后运用锐角三角函数即可得出DE.
解:(1)CD是⊙O的切线;
理由如下:连结OE,如图所示:
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,∴∠ADC=90°,∴∠OEC=90°,
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵∠OEC=90°,∠C=30°,
∴OC=2OE=2,
∴AC=3,
又∵∠ADC=90°,
∴AD=AC=,∠DAC=60°,
∵∠DAE=∠DAC=30°,
∴DE=AD tan30°=×=.
证明:(1)连接FO
易证OF∥AB
∵AC⊙O的直径
∴CE⊥AE
∵OF∥AB
∴OF⊥CE
∴OF所在直线垂直平分CE
∴FC=FE,OE=OC
∴∠FEC=∠FCE,∠0EC=∠0CE
∵Rt△ABC
∴∠ACB=90°
即:∠0CE+∠FCE=90°
∴∠0EC+∠FEC=90°
即:∠FEO=90°
∴FE为⊙O的切线
(2)
∵⊙O的半径为3
∴AO=CO=EO=3
∵∠EAC=60°,OA=OE
∴∠EOA=60°
∴∠COD=∠EOA=60°
∵在Rt△OCD中,∠COD=60°,OC=3
∴CD=
∵在Rt△ACD中,∠ACD=90°,
CD=,AC=6
∴AD=
版权所有@21世纪教育网(www.21cnjy.com)
直线与圆的位置关系单元检测B卷
姓名:__________班级:__________考号:__________
、选择题(本大题共10小题 )
已知⊙O的半径r=5,圆心O到直线l的距离为( )时,圆与直线l相交.
A. 7 B. 6 C. 5 D. 4
下列说法正确的是( )
A.与圆有公共点的直线是圆的切线
B.到圆心距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径外端的直线是圆的切线
如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径 C.AB是直径,B是切点 D.AB是直径,B是切点
已知⊙O的半径是5,直线是⊙O的切线,则点O到直线的距离是( )
A.2.5 B.3 C.5 D.10
已知如图,AB为半圆的直径,C、D为半圆弧上的两点,若弧CD=弧BD,DC与BA的延长线交于P,如果,AP:CP=3:4,△ADB的面积为,则AP的长为( )
A.7 B.12 C. D.4
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC,若∠A=36°,则∠C等于( )
A. 36° B. 54° C. 60° D. 27°
等腰三角形中,AB=AC,BC=4,△ABC的内切圆的半径为1,则AB的长为( )
A.2 B.3 C. D.
如图已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的圆O的切线交BC于点E,若CD=5,CE=4,则圆O的半径是( )
A.3 B.4 C. D.
Rt△ABC中,∠C=90°,AB=5,内切圆半径为1,则三角形的周长为( )
A.15 B.12 C.13 D.14
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A. B. C. D.
将正方形ABCD绕点A按逆时针方向旋转,得正方形,交CD于点E,AB=,则四边形的内切圆半径为( )
A. B. C. D.
、填空题(本大题共6小题 )
如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .
如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
如图,从点P引⊙O的切线PA,PB,切点分别为A,B,DE切⊙O于C,交PA,PB于D,E.若△PDE的周长为20cm,则PA= cm.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为______.
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
、解答题(本大题共8小题 )
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
求证:CA是圆的切线.
如图,延长⊙O的半径OC到A,使CA=OC,再作弦BC=OC.求证:直线AB是⊙O的切线.
如图,在△ABC中,,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E.
(1)求半圆O的半径;
(2)求图中阴影部分的面积.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
(1)求证:AB=DN;
(2)试判断CP与⊙O的位置关系,并证明你的结论.
如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线.
如图,为正方形对角线AC上一点,以为圆心,长为半径的⊙与相切于点.
(1)求证:与⊙相切;
(2)若⊙的半径为1,求正方形的边长.
如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF延长线于点D,交AB延长线于点C.
(1)判断CD是否是⊙O的切线,并说明理由.
(2)若∠C=30°,⊙O的半径为1,求DE的长.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
答案解析
、选择题
【分析】 直接根据直线和圆相交的条件即可得出结论.
解:∵⊙O的半径r=5,圆与直线l相交,
∴圆心O到直线l的距离d<5.
故选D.
【分析】根据切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.
解:A.与圆只有一个交点的直线是圆的切线,故本选项错误;
B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;
C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;
D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.
故选B.
【分析】根据圆的切线的判定方法“圆的切线垂直于经过切点的半径”,进行分析.
解:根据切线的判定方法,则这里的AB是直径,且一端是切点.
故选C.
【分析】根据直线与圆的位置关系可直接得到点O到直线l的距离如果⊙O的半径为r,圆心O到直线l的距离为d,那么直线l和⊙O相切 d=r;所以点O到直线的距离等于半径.
解:∵直线l与半径为r的⊙O相切,
∴点O到直线l的距离等于圆的半径,
即点O到直线l的距离为5.
故选C.
【分析】连OD、AC可以根据平行线分线段成比例定理的逆定理证明AC∥OD,则CD即可利用圆的半径表示出来,进而表示出BD,在直角△ABD中利用勾股定理即可求得AD,再根据△ADB的面积为可以得到关于半径的方程求得圆的半径,利用切割线定理即可求解.
解:设AO=R,连OD、AC.
∵=
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴AC∥OD,
∴==,
∴CD=R,
∴BD=R,
∴AD===R,
由S△AOB=16,
得: =16,
∴R=6,
∵PA PB=PC PD,设PA=x,则x(x+12)=x(x+8),
∴x=.
故PA=.
故选C.
【分析】根据题目条件易求∠BOA,根据圆周角定理求出∠C=∠BOA,即可求出答案.
∵AB与⊙O相切于点B,
∴∠ABO=90°,
∵∠A=36°,
∴∠BOA=54°,
∴由圆周角定理得:∠C=∠BOA=27°,
故选D.
【分析】利用三角形内切圆的性质以及切线长定理得出BD=BE,CE=CF,AD=AF,进而得出△ADF是等边三角形,即可得出答案.
解:∵△ABC的内切圆O与三边分别切于D、E、F,CB=6cm,△ABC的周长为16cm,
∴BD=BE,CE=CF,AD=AF,
∵BE+EC=BD+FC=6,
∴AD=AF=(AB+AC+BC-BC-BD-CF)=(16-6-6)=2,
∵∠A=60°,
∴△ADF是等边三角形,
∴DF=2.
故选:A.
解:连接OD,DB
【分析】根据切线的性质得出∠ODC=∠OFC=∠ACB=90°,得出正方形ODCF,求出CD=CF=1,根据切线长定理求出AD+BF=AE+BE=5,代入AC+BC+AB求出即可.
解:连接OA.OB、OC、OD、OE、OF,
∵⊙O是△ABC的内切圆,切点分别是D、E、F,
∴OD⊥AC,OE⊥AB,OF⊥BC,AD=AE,BE=BF,
∴∠ODC=∠OFC=∠ACB=90°,
∵OD=OF,
∴四边形ODCF是正方形,
∴CD=OD=OF=CF=1,
∵AD=AE,BF=BE,
∵AE+BE=AB=5,
∴AD+BF=5,
∴△ABC的周长是:AC+BC+AB=AD+CD+CF+BF+AB=5+1+1+5=12.
故选B.
【分析】过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解
解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=
∴CD=2,
∴图中阴影部分的面积为:-=
故选:A
解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
则∠OAF=30°,∠AB1O=45°,
故B1F=OF=OA,
设B1F=x,则AF=﹣x,
故(﹣x)2+x2=(2x)2,
解得x=或x=(舍去),
∴四边形AB1ED的内切圆半径为:.
故选:B.
、填空题
【分析】有条件可得AD=CD,再有切线长定理可得:CD=CE,所以AD=CE,问题的解.
解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
【分析】首先根据勾股定理求得该直角三角形的斜边是5,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解:∵直角三角形两直角边为3,4,
∴斜边长==5,
∴外接圆半径==2.5,内切圆半径==1,
∴外接圆和内切圆半径之和=2.5+1=3.5.
故答案为:3.5.
【分析】根据直线与圆的位置关系和直线与圆的交点个数以及命题中的数据分析即可得到答案.
解:(1)当d=3时,
∵3>2,即d>r,
∴直线与圆相离,则m=1,
故答案为:1;
(2)当m=2时,则圆上到直线l的距离等于1的点的个数记为2,
∴直线与圆相交或相切或相离,
∴0<d<3,
∴d的取值范围是0<d<3,
故答案为:0<d<3.
【分析】连接AO并延长交BC于D点,过点O作OE⊥AB于E,得到△AOE∽△ABD,再根据相似三角形对应边的比等于相似比进行计算求出AB边的长.
解:如图:
连接AO并延长交BC于点D,因为△ABC是等腰三角形,⊙O是△ABC的内切圆,
所以AD垂直平分BC,BD=CD=2,点O作OE⊥AB于E,
则点E是AB与⊙O的切点,由切线长定理得:BE=BD=2,
∴∠AEO=∠ADB=90°,∠OAE=∠BAD,
∴△AEO∽△ADB
∴=
∴=
解得:AE=,
∴AB=+2=.
故选D.
【分析】根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=÷2=58°,
∴∠BEC=180°﹣58°=122°.
故答案为:122°.
【分析】由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线;再利用角平分线的定义可知∠OBC+∠OCB=(∠ABC+∠ACB),代入数值即可求∠BOC=115°.
解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°﹣65°=115°.
、解答题
【分析】由BC为圆的直径,利用直径所对的圆周角为直角,得到△BDC为直角三角形,利用直角三角形的两锐角互余得到一对角互余,再由已知的角相等,等量代换可得出AC与BC垂直,进而确定出CA为圆的切线.
证明:∵BC为圆的直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
又∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,即∠ACB=90°,
∴AC⊥BC,BC为圆的直径,
∴CA为圆的切线.
【分析】连OB,要直线AB是⊙O的切线,即证明OB⊥BA即可.由BC=OC,CA=OC,即BC=CA=CB,则得到△OBA为直角三角形,所以有OB⊥BA.
证明:连OB,如图,
∵BC=OC,CA=OC,
∴BC为△OBA的中线,且BC=OA,
∴△OBA为直角三角形,
即OB⊥BA.
所以直线AB是⊙O的切线.
(1)解:连结OD,OC,
∵半圆与AC,BC分别相切于点D,E.
∴,且.
∵,
∴且O是AB的中点.
∴.
∵,∴.
∴.
∴在中,.
即半圆的半径为1.
【分析】(1)根据圆周角定理得到∴∠ACB=90°,则∠NCD=90°,而DM⊥AB,根据等角的余角相等得到∠A=∠D,然后根据“ASA”判断△ABC≌△DNC,则AB=DN;
(2)根据直角三角形斜边上的中线性质得PC=PN=,则∠PCN=∠PNC,所以∠ANM=∠PCN,而∠A=∠ACO,于是得到∠ACO+∠PCN=90°,
即∠PCO=90°,然后根据切线的判定定理得到CP是⊙O的切线.
(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,则∠NCD=90°,
∵DM⊥AB,
∴∠AMN=90°,
∴∠ABC+∠A=∠ABC+∠D=90°,
∴∠A=∠D,
在△ABC和△DNC中
,
∴△ABC≌△DNC(ASA),
∴AB=DN;
(2)CP是⊙O的切线.理由如下:
连结OC,如图,
∵CP是△CDN的边ND上的中线,∠NCD=90°,
∴PC=PN=,
∴∠PCN=∠PNC,
∵∠ANM=∠PNC,
∴∠ANM=∠PCN,
∵OA=OC,
∴∠A=∠ACO,
∵∠A+∠ANM=90°,
∴∠ACO+∠PCN=90°,
∴∠PCO=90°,
∴OC⊥PC
∴CP是⊙O的切线.
【分析】直接根据圆周角定理求解;
(2)根据圆周角定理,由AB是⊙O的直径得∠ACB=90°,则利用互余可计算出∠BAC=30°,于是得到∠BAE=∠BAC+∠EA=90°,然后根据切线的判定定理得到结论.
(1)解:∵∠D=60°,
∴∠ABC=∠D=60°;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣60°=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
∴BA⊥AE,
∴AE是⊙O的切线.
(1)证明:连接OM,过点O作ON⊥CD,垂足为N,
∵⊙0与BC相切于M,
∴OM⊥BC,
∵正方形ABCD中,AC平分∠BCD,
又∵ON⊥CD,OM⊥BC
∴OM=ON
∴CD与⊙O相切
(2)由(1)易知为等腰直角三角形,OM为半径,
∴ OM=MC=1.
∴ ,
∴
∴
在中,AB=BC,
有
∴
∴ .
故正方形的边长为.
【分析】(1)先证OE∥AD,得出∠ADC=∠OEC,再由AD⊥CD,证出OE⊥CD,即可得出结论;
(2)由∠C=30°,得出OC=2OE=2,AC=3,再根据含30°的直角三角形的性质求出AD,然后运用锐角三角函数即可得出DE.
解:(1)CD是⊙O的切线;
理由如下:连结OE,如图所示:
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,∴∠ADC=90°,∴∠OEC=90°,
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵∠OEC=90°,∠C=30°,
∴OC=2OE=2,
∴AC=3,
又∵∠ADC=90°,
∴AD=AC=,∠DAC=60°,
∵∠DAE=∠DAC=30°,
∴DE=AD tan30°=×=.
证明:(1)连接FO
易证OF∥AB
∵AC⊙O的直径
∴CE⊥AE
∵OF∥AB
∴OF⊥CE
∴OF所在直线垂直平分CE
∴FC=FE,OE=OC
∴∠FEC=∠FCE,∠0EC=∠0CE
∵Rt△ABC
∴∠ACB=90°
即:∠0CE+∠FCE=90°
∴∠0EC+∠FEC=90°
即:∠FEO=90°
∴FE为⊙O的切线
(2)
∵⊙O的半径为3
∴AO=CO=EO=3
∵∠EAC=60°,OA=OE
∴∠EOA=60°
∴∠COD=∠EOA=60°
∵在Rt△OCD中,∠COD=60°,OC=3
∴CD=
∵在Rt△ACD中,∠ACD=90°,
CD=,AC=6
∴AD=
版权所有@21世纪教育网(www.21cnjy.com)
