5.2 等式的基本性质课件

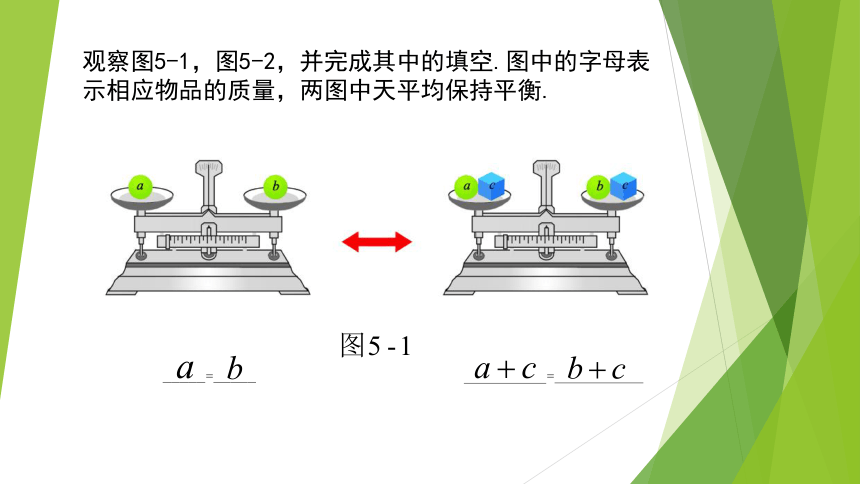
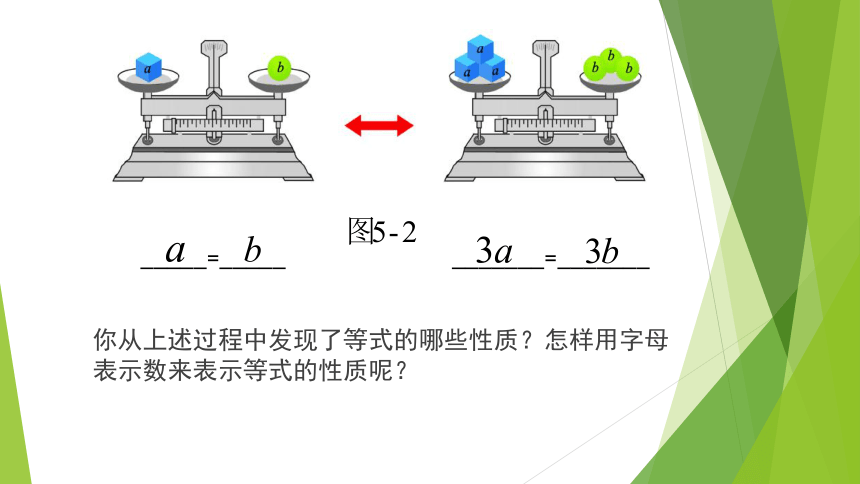
课件15张PPT。比较左、右两个天平图，你发现了什么？等式的基本性质观察图5-1，图5-2，并完成其中的填空.图中的字母表示相应物品的质量，两图中天平均保持平衡. _____=_____ = . _____=_____ _______=_______你从上述过程中发现了等式的哪些性质？怎样用字母表示数来表示等式的性质呢？一般地，等式有以下的基本性质：等式的性质1 等式的两 都加上（或都减去）同一个数或式，所得结果仍是等式.用字母可以表示为：
如果 ，那么 .等式的性质2 等式的两边都乘或都除以同一个数或式（除数不能为零），所得结果仍是等式.用字母可以表示为：
如果 ，那么 ，或 .等式的两边等式的两边同一个数或式同一个数或式除数不能为零已知 ，下列等式成立吗？根据是什么？⑴⑵⑶⑷做一做例1 已知 ，且 ，判断下列等式是否成立，并说明理由.⑴ ；⑵ .解 ⑴成立.理由如下：已知 ，两边都加上5y，得 （等式的性质1）， ⑵成立. 理由如下：由第⑴题知 ，而 ，两边都除以2y ，得 （等式的性质2）. 方程是含有未知数的等式,方程中的未知数与已知数一起参与了运算.通过运算将一元一次方程一步一步变形,最后变形成“x＝a(a为已知数)”的形式,就求出了未知数的值,即方程的解.等式的性质是方程变形的依据.例2 利用等式的性质解下列方程：
⑴ . ⑵ .解 ⑴方程的两边都减去4x ，得（等式的性质 1），合并同类项，得检验：把 代入方程，左边=5×50=250，右边=50+4×50.∵左边=右边，是方程的解. ⑵方程的两边都加上 ，得合并同类项，得两边都减去8，得两边都除以2，得 （根据什么？）.归纳 用等式的基本性质解一元一次方程，将方程一步一步变形成“x = a（a为已知数）”的形式，体现了一种转化的思想.方程变形转化的思想和步骤为：
通过等式的性质 1，先将含有未知数的项移到方程的 .不含未知数的项移到方程的 .再通过等式的性质 2，在方程两边同除以未知数项的 .最后化成“x=a（ a为已知数）”的形式.左边右边系数1.已知 ，求：⑴说明2a=-3b成立的理由；⑵ a与b的比为多少？解：⑴等式两边都乘以6，得2a+3b=0(等式的性质2）.等式两边都减去3b，得2a=-3b.⑵在等式2a=-3b的两边同除以2b，得拓展2.将等式 2a=2b 的两边都减去 a+b，可得a-b=b-a，再两边都除以(a-b)，得 1=-1.这个结果显然是错误的！你知道错在哪里吗？解因为除数不能为0，所以等式两边不能都除以a-b.1.根据下列各题的条件，写出仍然成立的等式.⑴ ，两边都加上b.⑵ ，两边都减去 2a.⑶ ，两边都乘6.2.利用等式的性质解下列方程，并写出检验过程.⑴⑵解将 代入原方程：左边=5×2-3=7.∴左边=右边.∴ 是原方程的解.解将 代入原方程：左边=4×4-1=15.右边=3×4+3=15.∴左边=右边.∴ 是原方程的解.3.已知 ，且 ，求y与x的比.解 由 ，得 .，两边同除以 ,得课后作业作业本 5.2节 等式的基本性质
预习5.3节