4.4 两个三角形相似的判定(1) 课件
文档属性
| 名称 | 4.4 两个三角形相似的判定(1) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-22 00:00:00 | ||
图片预览


文档简介
课件10张PPT。4.4两个三角形相似的判定(1) 2、三角形的中位线截得的三角形与原三角形是否相似?相似比是多少?
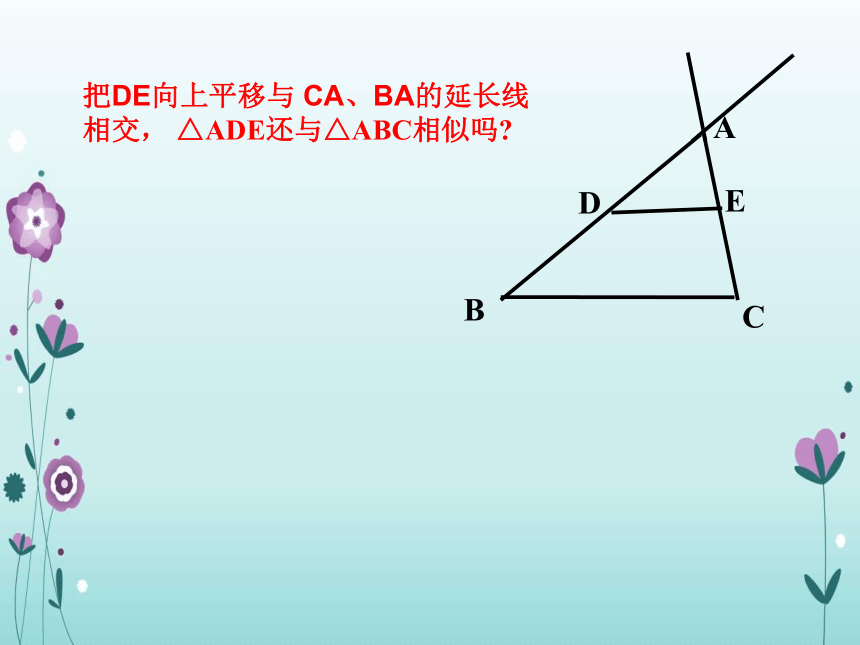
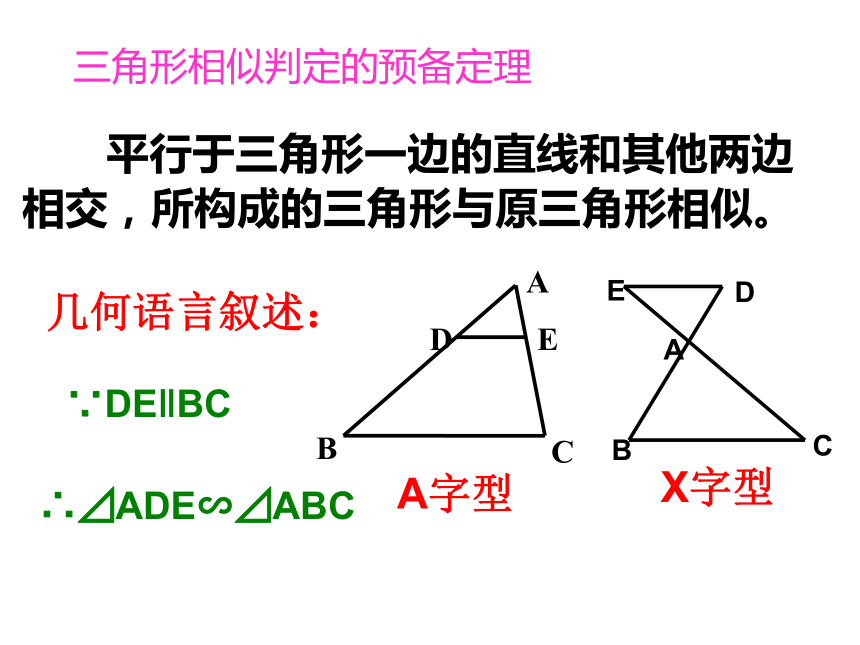
1、相似三角形的定义?对应角相等,对应边成比例的两个三角形叫做相似三角形.第一关3 、如图,在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?由此你能得出什么结论?平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。DE把DE向上平移与 CA、BA的延长线相交, △ADE还与△ABC相似吗? 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。三角形相似判定的预备定理∵DE‖BC几何语言叙述:∴⊿ADE∽⊿ABC
A字型X字型 相似三角形判定定理1:
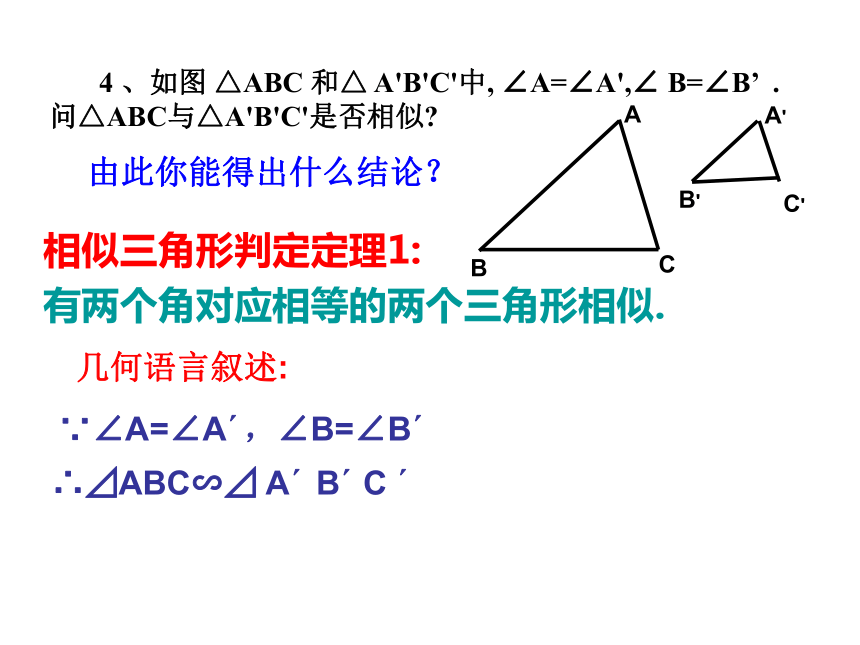
有两个角对应相等的两个三角形相似.几何语言叙述:∵∠A=∠A′,∠B=∠B′∴⊿ABC∽⊿ A′ B′ C ′ 4 、如图 △ABC 和△ A'B'C'中, ∠A=∠A',∠ B=∠B’ . 问△ABC与△A'B'C'是否相似?由此你能得出什么结论? △ABC∽△ACD∽△CBD.
已知,如图Rt△ABC中,CD是斜边上的高.
(1)请找出图中的相似三角形.(2)求证:AC2=AD·AB. 证明:∵ △ABC∽△ACD ,
∴AB:AC=AC:AD
∴AC2=AD·AB借助三角形相似产生比例线段求线段长是常用方法。(3)若AD=2,BD=8,求CD的长. 解:∵ △ADC∽△CDB ,
∴AD:CD=CD:BD
∴2:CD=CD:8
∵CD>0,
∴CD=4第二关 (1)如图,在ΔABC中 ,点D是AB边上的点,请在AC边上找一点E,使得ΔADE与 ΔABC相似? BD第三关 (2)在ΔABC中 ,AB=10, AC=7, BC=8,点D是AB边上的点,AD=4, 点E是AC边上的点,连结DE, 若ΔADE与 ΔABC相似,求DE的长。 借助三角形相似产生比例线段求线段长是常用方法。 在一次数学活动课上,为了测量河宽AB,小明采用了如下的方法:从A处沿与AB垂直的直线方向走45米到达C处,插一根标竿,然后沿同方向继续走15米到达D处,F构造三角形相似产生比例线段求线段长是常用方法。第四关再向右转90度走到E处,使B、C、E三点恰好在一条直线上,量得DE=20米,这样就可以求出河宽AB,请你说明理由,并算出结果。判定两个三角形相似的方法:
1、相似三角形的定义
2、预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
3、判定定理1:
有两个角对应相等的两个三角形相似.我的收获感言:老师的赠言:在数学中,最令我欣喜的,是那些能够被证明的东西。数学是人类智慧皇冠上最灿烂的明珠。谢谢大家
1、相似三角形的定义?对应角相等,对应边成比例的两个三角形叫做相似三角形.第一关3 、如图,在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?由此你能得出什么结论?平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。DE把DE向上平移与 CA、BA的延长线相交, △ADE还与△ABC相似吗? 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。三角形相似判定的预备定理∵DE‖BC几何语言叙述:∴⊿ADE∽⊿ABC
A字型X字型 相似三角形判定定理1:
有两个角对应相等的两个三角形相似.几何语言叙述:∵∠A=∠A′,∠B=∠B′∴⊿ABC∽⊿ A′ B′ C ′ 4 、如图 △ABC 和△ A'B'C'中, ∠A=∠A',∠ B=∠B’ . 问△ABC与△A'B'C'是否相似?由此你能得出什么结论? △ABC∽△ACD∽△CBD.
已知,如图Rt△ABC中,CD是斜边上的高.
(1)请找出图中的相似三角形.(2)求证:AC2=AD·AB. 证明:∵ △ABC∽△ACD ,
∴AB:AC=AC:AD
∴AC2=AD·AB借助三角形相似产生比例线段求线段长是常用方法。(3)若AD=2,BD=8,求CD的长. 解:∵ △ADC∽△CDB ,
∴AD:CD=CD:BD
∴2:CD=CD:8
∵CD>0,
∴CD=4第二关 (1)如图,在ΔABC中 ,点D是AB边上的点,请在AC边上找一点E,使得ΔADE与 ΔABC相似? BD第三关 (2)在ΔABC中 ,AB=10, AC=7, BC=8,点D是AB边上的点,AD=4, 点E是AC边上的点,连结DE, 若ΔADE与 ΔABC相似,求DE的长。 借助三角形相似产生比例线段求线段长是常用方法。 在一次数学活动课上,为了测量河宽AB,小明采用了如下的方法:从A处沿与AB垂直的直线方向走45米到达C处,插一根标竿,然后沿同方向继续走15米到达D处,F构造三角形相似产生比例线段求线段长是常用方法。第四关再向右转90度走到E处,使B、C、E三点恰好在一条直线上,量得DE=20米,这样就可以求出河宽AB,请你说明理由,并算出结果。判定两个三角形相似的方法:
1、相似三角形的定义
2、预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
3、判定定理1:
有两个角对应相等的两个三角形相似.我的收获感言:老师的赠言:在数学中,最令我欣喜的,是那些能够被证明的东西。数学是人类智慧皇冠上最灿烂的明珠。谢谢大家
同课章节目录
