5.5一次函数的简单应用（2）练习题

21世纪教育网 –中小学教育资源及组卷应用平台
5.5 一次函数的简单应用（2）
班级：___________姓名：___________得分：__________
一、选择题
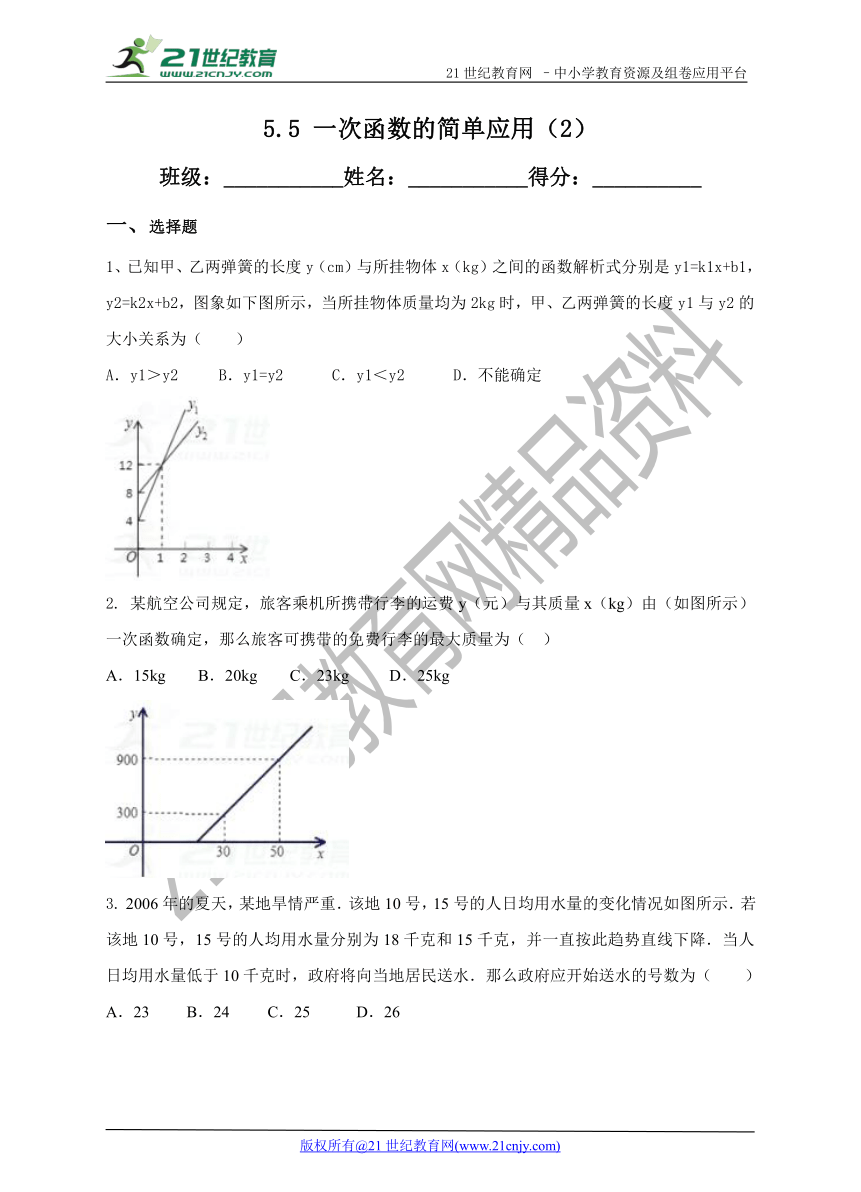
1、已知甲、乙两弹簧的长度y（cm）与所挂物体x（kg）之间的函数解析式分别是y1=k1x+b1，y2=k2x+b2，图象如下图所示，当所挂物体质量均为2kg时，甲、乙两弹簧的长度y1与y2的大小关系为（　　）21cnjy.com
A．y1＞y2 B．y1=y2 C．y1＜y2 D．不能确定
2. 某航空公司规定，旅客乘机所携带行李的运费y（元）与其质量x（kg）由（如图所示）一次函数确定，那么旅客可携带的免费行李的最大质量为（ ）21世纪教育网版权所有
A．15kg B．20kg C．23kg D．25kg
3. 2006年的夏天，某地旱情严重．该地10号，15号的人日均用水量的变化情况如图所示．若该地10号，15号的人均用水量分别为18千克和15千克，并一直按此趋势直线下降．当人日均用水量低于10千克时，政府将向当地居民送水．那么政府应开始送水的号数为（　　）
A．23 B．24 C．25 D．26
4. 在一次远足活动中，小聪和小明由甲地步行到乙地后原路返回，小明在返回的途中的丙地时发现物品可能遗忘在乙地，于是从丙返回乙地，然后沿原路返回．两人同时出发，步行过程中保持匀速．设步行的时间为t（h），两人离甲地的距离分别为S1（km）和S2（km），图中的折线分别表示S1、S2与t之间的函数关系．则下列说法中正确的是（　　）
A．甲、乙两地之间的距离为20km
B．乙、丙两地之间的距离为4km
C．小明由甲地出发首次到达乙地的时间为 小时
D．小明乙地到达丙地用了小时
5. 甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留）前往终点B地，甲、乙两车的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，小红通过图象得出以下4个信息：21·cn·jy·com
①甲车速度为60千米/小时；
②A、B两地相距240千米；
③乙车行驶2小时追上甲车；
④乙车由A地到B地共用3小时．
上述信息正确的有（　　）个．
A．1 B．2 C．3 D．4
二、填空题
1、某班带队到展览馆参观，并要求作好记录，小亮随队伍步行一段时间后，发现未带笔记本，随即跑步返回拿到笔记本后又以相同的速度追赶队伍，恰好与队伍在同一时间到达展览馆．行程与时间的关系如图所示，其中实线表示队伍的图象，虚线表示小亮的图象，则小亮跑步的速度为______米/分钟．www.21-cn-jy.com
2. 某汽车生产厂对其生产的A型汽车进行耗油量实验，实验中汽车视为匀速行驶．
已知油箱中的余油量y（升）与行驶时间t（小时）的关系如下表，
行驶时间t（时） 0 1 2 3
油箱余油量y（升） 100 84 68 52
与行驶路程x（千米）的关系如图．则A型车在实验中的速度是______千米/时．
3. 如图，lA，lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．若B的自行车不发生故障，保持出发时的速度前进，则与A相遇时，相遇点C的坐标是______．
4. 一慢车和一快车沿相同路线从A地到相距120千米的B地，所行地路程与时间的函数图像如图所示，试根据图像，回答下列问题：2·1·c·n·j·y
（1）慢车比快车早出发（ ）小时，快车比慢车少用（ ）小时到达B地；
（2）快车用（　　）小时追上慢车；此时相距A地（　　）千米。
5. 汽车燃油价税费改革从2009年元旦起实施： 取消养路费，同时汽油消费税每升提高0.8元。若某车一年的养路费是1440元,百公里耗油8升，在“费改税”前后该车的年支出与年行驶里程的关系分别如图中的l1、l2所示，则l1与l2的交点的横坐标m=_____ (不考虑除养路费和燃油费以外的其它费用) 。【来源：21·世纪·教育·网】
三、解答题
1. 小丽一家利用元旦三天驾车到某景点旅游，小汽车出发前油箱有油36L，行驶若干小时后，中途在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的关系如图所示，根据图象回答下列问题：21·世纪*教育网
（1）汽车行驶______h后加油，中途加油______L；
（2）求加油前油箱余没油量Q与行驶时间t之间的函数关系式；
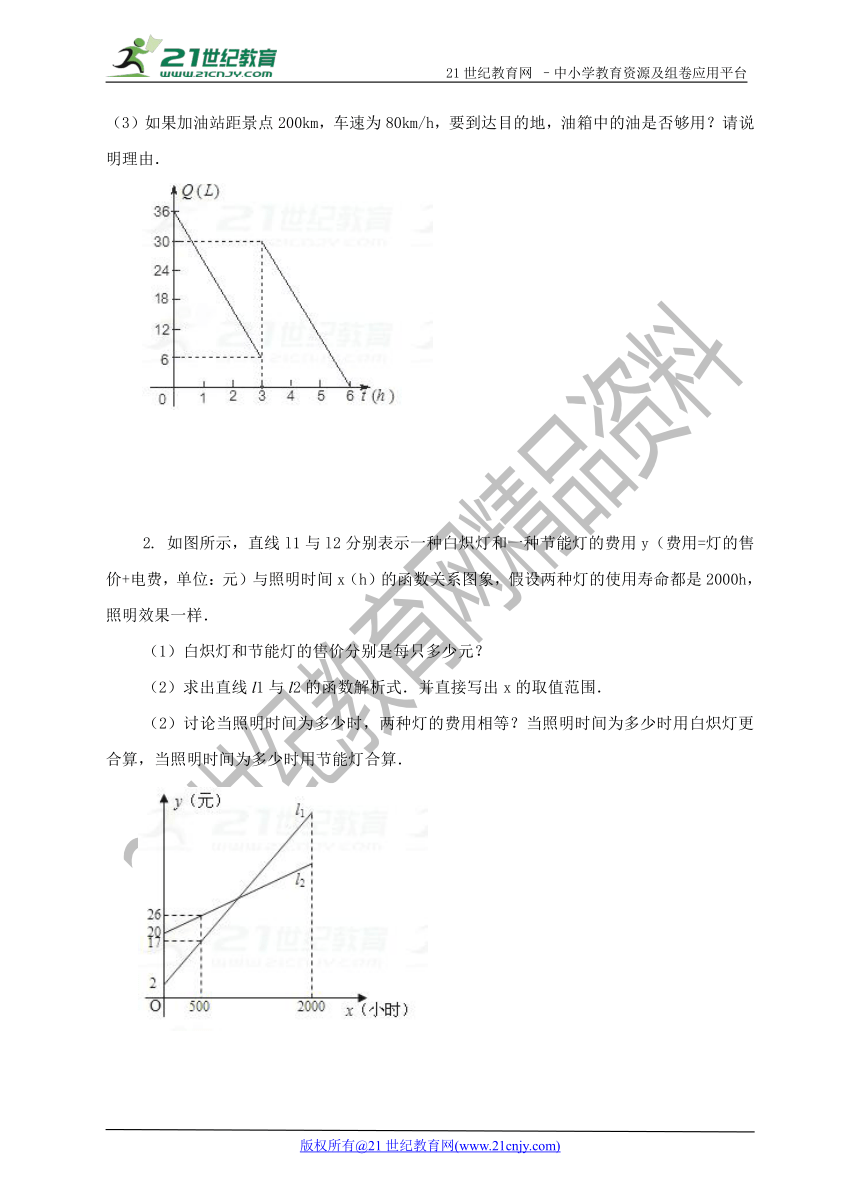
（3）如果加油站距景点200km，车速为80km/h，要到达目的地，油箱中的油是否够用？请说明理由．www-2-1-cnjy-com
2. 如图所示，直线l1与l2分别表示一种白炽灯和一种节能灯的费用y（费用=灯的售价+电费，单位：元）与照明时间x（h）的函数关系图象，假设两种灯的使用寿命都是2000h，照明效果一样．2-1-c-n-j-y
（1）白炽灯和节能灯的售价分别是每只多少元？
（2）求出直线l1与l2的函数解析式．并直接写出x的取值范围．
（2）讨论当照明时间为多少时，两种灯的费用相等？当照明时间为多少时用白炽灯更合算，当照明时间为多少时用节能灯合算．21*cnjy*com
参考答案
一、选择题
1、A
【解析】∵点（0，4）和点（1，12）在y1=k1x+b1上，
∴得到方程组：
4＝b1
12＝k1+b1
解得：
K1＝8
B1＝4
∴y1=8x+4．
∵点（0，8）和点（1，12）代入y2=k2x+b2上，
∴得到方程组为
8＝b2
12＝k2+b2
解得：
K2＝4
B2＝8
∴y2=4x+8．
当x=2时，y1=8×2+4=20，y2=4×2+8=16，
∴y1＞y2．
故选A．
2、B
【解析】设一次函数的解析式为y=kx+b，
∵点（30，300），（50，900）在函数的解析式上，代入y=kx+b中，
可求得k=30，b=-600，
∴函数的解析式为y=30x-600．
求旅客最多可携带免费行李的最大重量即是求一次函数与x轴交点横坐标．
令y=0，可求得x=20．
∴旅客最多可携带免费行李的最大重量为20kg．
3、B
【解析】设号数为x，用水量为y千克，直线解析式为y=kx+b．
根据题意得
18=10k+b
15=15k+b ，解之得
k= - b=24 ，
所以直线解析式为y= - x+24，
当y=10时，有- x+24=10，解之得x=23 ，
根据实际情况，应在24号开始送水．
故选B．
4.C
【解析】根据图中信息，甲、乙两地之间的距离为10km，乙、丙两地之间的距离为2km；
故选项A，B错误；
根据小明到达丙时所用时间为1小时，所行路程为（10+2）km，
即v2=（10+2）÷1=12km/h，
t1=10÷12= （小时），t2=2÷12= （小时），
故小明由甲地出发首次到达乙地用了小时，故选项C正确，
由乙地到达丙地用了 小时，故D选项错误．
故选：C．
5.B
【解析】由函数图象及题意可以得出：
甲车的速度为：15÷（4- ）=45km/时，故①错误；
A、B两地的路程为：45×4=180km，故②错误；
乙车追上甲车的时间是- =2小时，故③正确；
乙车由A地去B地的时间为 - =3小时，故④正确．
综上所述，正确的由2个．
故选B．
二、填空题
1、200
【解析】设队伍前进时的函数关系式为y=kx，
把点（24，1200）代入得：1200=24k，
解得：k=50，
∴解析式为y=50x，
队伍走到展览馆所用的时间为：2000÷50=40（分钟），
则小亮返回之后队伍走到展览馆所用的时间为：40-24=16（分钟），
根据图象可知，小亮返回之后到到达展览馆走的路程为：1200+2000=3200米，
∴小亮跑步的速度为：3200÷16=200（米/分钟）
故答案为：200．
2、100
【解析】设油箱中的余油量y与行驶路程x（千米）的函数关系为y=kx+b，
由题意得
b=100 20=500k+b ，
解之得b=100，k=-0.16，
∴y=-0.16x+100，
设油箱中的余油量y（升）与行驶时间t（小时）的函数关系为y=kt+b，
由题意得
b=100
84=k+b ，
解之得b=100，k=-16，
∴y=-16t+100，
当y=50时，x= ，t= ，
∴速度v= ÷ =100千米/时．
故答案为：100．
3、（1，15）
【解析】若B的自行车不发生故障，保持出发时的速度前进，图象是正比例函数解析式，
∴s=at，图象经过点（0.5，7.5），
∴s=15t，
S A=at+b，图象经过（0，10），（3，25），
∴b＝10
25＝3a+b，
∴a＝5
b＝10，
∴S A=5t+10；
∴s＝15t
s ＝5t+10，
∴15t=5t+10；
∴t=1，S=15，
∴点C的坐标是（1，15）．
故答案为：（1，15）
4.（1）2, 8 （2）2.5 ，30
【解析】（1）由图象可得；慢车比快车早出发2小时，
快车从A地到B地共用；12-2=10（小时），
慢车从A地到B地共用：18小时，
∴快车比慢车少用18-10=8小时到达B地；
故答案为：2，8；
当x=12x-24时，快车追上慢车，
解得：x=4.5，
y=×4.5=30（千米），
4.5-2=2.5（小时）．
∴快车用了2.5小时时间追上慢车；此时相距A地30千米．
5. 22500
【解析】设每升汽油的价格为a元，
由题意可知l1=（×a）x+1440，
l2=（a+0.8）×x，
令l1=l2，
解得x=22500．
故l1与l2的交点的横坐标m为22500．21教育网
三、解答题
1.【解析】（1）从图中可知汽车行驶3h后加油，中途加油24L；
（2）根据分析可知Q=-10t+36（0≤t≤3）；
（3）油箱中的油是够用的．
∵200÷80=2.5（小时），需用油10×2.5=25L＜30L，
∴油箱中的油是够用的．
2. 【解析】解：（1）设l1的解析式为y1=k1x+b1，L2的解析式为y2=k2x+b2
由图可知l1过点（0，2），（500，17）
∴ 2=b1
17=500k1+b1
∴k1=0.03，b1=2
∴y1=0.03x+2（0≤x≤2000）
由图可知l2过点（0，20），（500，26）， 同理y2=0.012x+20（0≤x≤2000）
（2）两种费用相等，即y1=y2， 则0.03x+2=0.012x+20， 解得x=1000
∴当x=1000时，两种灯的费用相等
（3）显然前2000h用节能灯，剩下的500h，用白炽灯。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)