浙教版八下数学第五章 特殊平行四边形同步练习(附答案)
文档属性
| 名称 | 浙教版八下数学第五章 特殊平行四边形同步练习(附答案) | 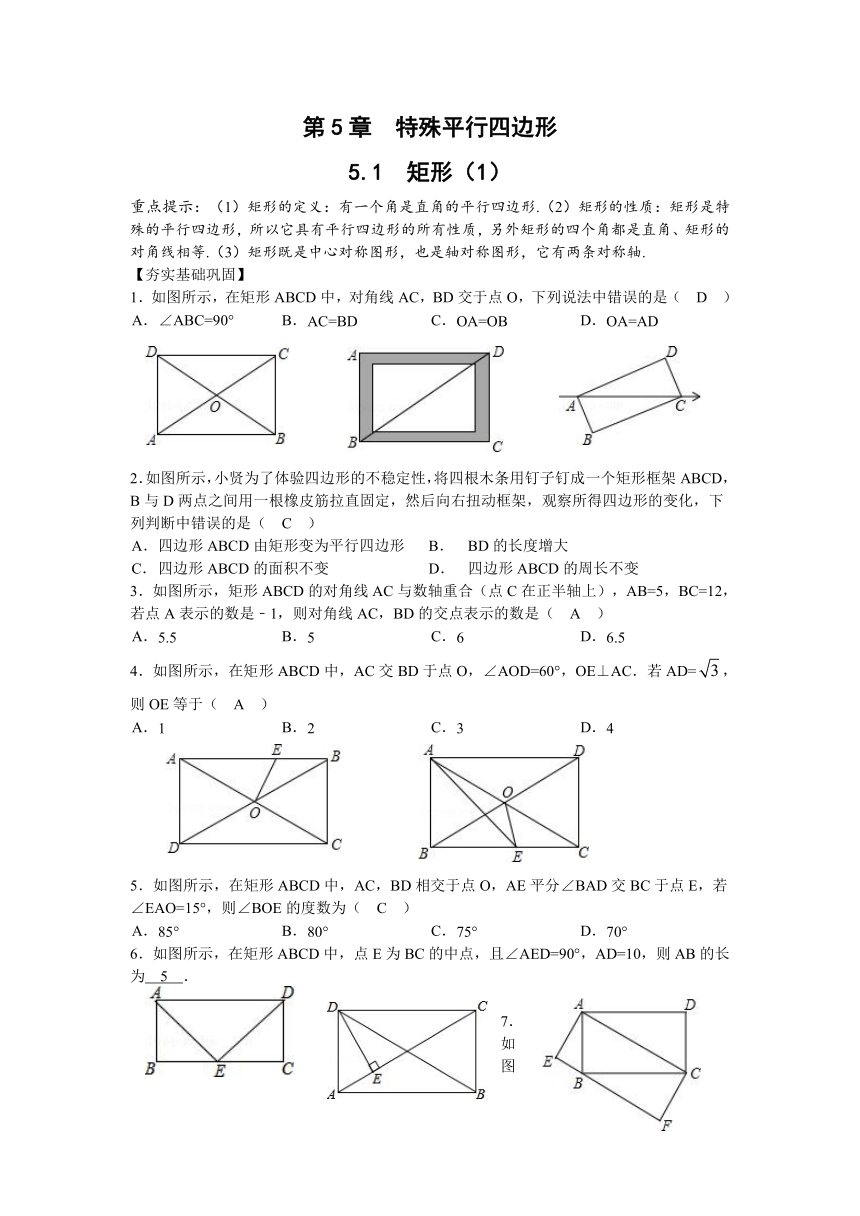 | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-24 22:31:07 | ||
图片预览




文档简介
第5章 特殊平行四边形
5.1 矩形(1)
重点提示:(1)矩形的定义:有一个角是直角的平行四边形.(2)矩形的性质:矩形是特殊的平行四边形,所以它具有平行四边形的所有性质,另外矩形的四个角都是直角、矩形的对角线相等.(3)矩形既是中心对称图形,也是轴对称图形,它有两条对称轴.
【夯实基础巩固】
1.如图所示,在矩形ABCD中,对角线AC,BD交于点O,下列说法中错误的是( D )
A.
∠ABC=90°
B.
AC=BD
C.
OA=OB
D.
OA=AD
2.如图所示,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断中错误的是( C )
A.
四边形ABCD由矩形变为平行四边形
B.
BD的长度增大
C.
四边形ABCD的面积不变
D.
四边形ABCD的周长不变
3.如图所示,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,若点A表示的数是﹣1,则对角线AC,BD的交点表示的数是( A )
A.
5.5
B.
5
C.
6
D.
6.5
4.如图所示,在矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=,则OE等于( A )
A.
1
B.
2
C.
3
D.
4
5.如图所示,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠EAO=15°,则∠BOE的度数为( C )
A.
85°
B.
80°
C.
75°
D.
70°
6.如图所示,在矩形ABCD中,点E为BC的中点,且∠AED=90°,AD=10,则AB的长为 5 .
7.如图所示,在矩形ABCD中,DE⊥AC,∠ADE=∠CDE,则∠BDC的度数为 30° .
8.如图所示,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是S1 = S2( 填“>”“<”或“=”)
9.如图所示,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为点E,F.
求证:BE=CF.
∵四边形ABCD为矩形,∴AC=BD,则BO=CO.
∵BE⊥AC于点E,CF⊥BD于点F,∴∠BEO=∠CFO=90°.
∵∠BOE=∠COF,∴△BOE≌△COF.∴BE=CF.
10.如图所示,在矩形ABCD中, F是CD中点,连结AF并延长交BC的延长线于点E,连结AC.
(1)求证:△ADF≌△ECF.
(2)若AB=1,BC=2,求四边形ACED的面积.
(1)∵F是CD中点,
∴DF=CF.
∵四边形ABCD是矩形,
∴AD∥BC,即AD∥CE.
∴∠ADF=∠ECF.
在△ADF和△ECF中,∵
∴△ADF≌△ECF(ASA).
(2)∵四边形ABCD是矩形,∴AD=BC=2,AB=CD=1,CD⊥AD.
由(1)知,△ADF≌△ECF,∴AD=CE.
∵AD∥CE,∴四边形ACED是平行四边形.
∴S四边形ACED =2×1=2.
【能力提升培优】
11. 如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( D )
A.
8
B.
8
C.
4
D.
6
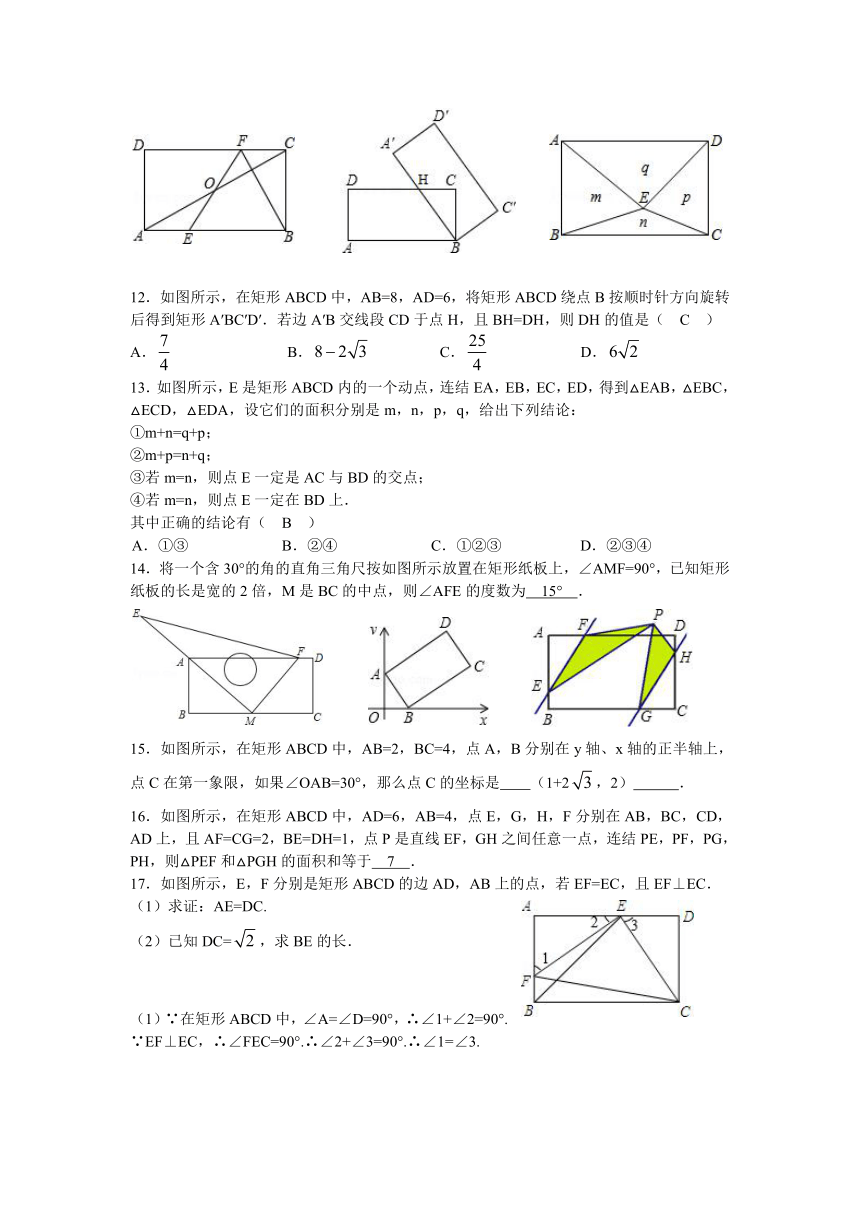
12.如图所示,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于点H,且BH=DH,则DH的值是( C )
A. B. C. D.
13.如图所示,E是矩形ABCD内的一个动点,连结EA,EB,EC,ED,得到△EAB,△EBC,△ECD,△EDA,设它们的面积分别是m,n,p,q,给出下列结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则点E一定是AC与BD的交点;
④若m=n,则点E一定在BD上.
其中正确的结论有( B )
A.
①③
B.
②④
C.
①②③
D.
②③④
14.将一个含30°的角的直角三角尺按如图所示放置在矩形纸板上,∠AMF=90°,已知矩形纸板的长是宽的2倍,M是BC的中点,则∠AFE的度数为 15° .
15.如图所示,在矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 (1+2,2) .
16.如图所示,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF,GH之间任意一点,连结PE,PF,PG,PH,则△PEF和△PGH的面积和等于 7 .
17.如图所示,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:AE=DC.
(2)已知DC=,求BE的长.
(1)∵在矩形ABCD中,∠A=∠D=90°,∴∠1+∠2=90°.
∵EF⊥EC,∴∠FEC=90°.∴∠2+∠3=90°.∴∠1=∠3.
在△AEF和△DCE中,∵
∴△AEF≌△DCE(AAS).∴AE=DC.
(2)由(1)得AE=DC,∴AE=DC=,
在矩形ABCD中,AB=CD=,
在Rt△ABE中,,即.
18.如图所示,点E是矩形ABCD的边BC的延长线上一点,连结AE交CD于点F,G是AF的中点,再连结DG,DE,且DE=DG.
(1)求证:∠DEA=2∠AEB.
(2)若BC=2AB,求∠AED的度数.
(1)∵四边形ABCD是矩形,∴∠ADF=90°,AD∥BC.
∵Rt△ADF中,G是AF中点,∴GA=GD=GF.∴∠DGF=2∠DAE.
∵AD∥BE,∴∠AEB=∠DAE.
∵DG=DE,∴∠DEA=∠DGF.∴∠DEA=2∠AEB.
(2)过点G作GH⊥DC于H.
∵AD∥GH,G是AF中点,∴GH=AD=AB=DC.
∵DE=DG=GF,∴Rt△GHF≌Rt△DCE(HL).
∵∠DEA=2∠AEB,∴∠DCE=∠GFH=3∠AEB=3∠DAE.
∵∠DAE+∠GFH=90°,∴4∠DAE=90°,∠DAE=22.5°.∴∠DEA=2∠DAE=45°.
【中考实战演练】
19.【鄂尔多斯】如图所示,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( D )
A.
14
B.
16
C.
17
D.
18
20.【攀枝花】如图所示,在平面直角坐标系中,O为坐标原点,在矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为 (2.5,4),(3,4),(2,4),(8,4) .
【开放应用探究】
21.如图所示,点E为矩形ABCD外一点,DE⊥BD于点D,DE=CE,BD的垂直平分线交AD于点F,交BD于点G.连结EF交BD于点H.
(1)若∠CDE=∠DEH=∠HEC,求∠ABG的度数.
(2)求证:H是EF的中点.
(1)设∠CDE=x°.
∵DE=CE,∴∠CDE=∠DCE=x°.
∵∠CDE=∠DEH=∠HEC,
∴∠DEH=x°,∠HEC=2x°.
∵∠CDE+∠DEC+∠DCE=180°,
∴5x=180,解得x=36.
∵DE⊥BD,∴∠EDB=90°.∴∠BDC=90°﹣36°=54°.
∵四边形ABCD是矩形,
∴AB∥CD.∴∠ABG=∠BDC=54°.
(2)如图所示,连结AC,GE,CD与GE交于点M.
∵四边形ABCD是矩形,
∴AC=BD,AG=GC,BG=GD.∴GD=GC.
∴点G在CD的垂直平分线上.∵DE=CE,
∴点E在CD的垂直平分线上.
∴GE为CD的垂直平分线.∴DM=CM.
∵BG=DG,∴GM∥BC.
∵□ABCD是矩形,∴AD∥BC.
∴FD∥GE.
∵FG⊥BD,DE⊥BD,∴FG∥DE.
∴四边形FDEG是平行四边形.∴H为EF的中点.
5.1 矩形(2)
重点提示:判定一个四边形是矩形有三种方法:(1)有一个角是直角的平行四边形是矩形.(2)有三个角是直角的四边形是矩形.(3)对角线相等的平行四边形是矩形.注意方法(1)和(3)要先利用平行四边形的判定方法证明四边形是平行四边形.
【夯实基础巩固】
1.在□ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出□ABCD是矩形,那么这个条件可以是( B )
A.
AB=BC
B.
AC=BD
C.
AC⊥BD
D.
AB⊥BD
2.下列说法中正确的是( C )
A.
两组对角分别相等的四边形是矩形
B.
两个角是直角的四边形是矩形
C.
一个角是直角的平行四边形是矩形
D.
一个角是直角,一组对边相等的四边形是矩形
3.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( D )
A.
测量对角线是否相互平分
B.
测量两组对边是否分别相等
C.
测量对角线是否相等
D.
测量其中三个角是否都为直角
4.如图所示,四边形ABCD的对角线AC,BD相交于点O,给出下列条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( C )
A.
①②③
B.
②③④
C.
②⑤⑥
D.
④⑤⑥
5.已知四边形ABCD的两条对角线AC,BD互相垂直,E,F,G,H分别是四边形ABCD各边的中点.若AC=6,BD=8,则四边形EFGH的面积为( C )
A.48 B.24 C.12 D.条件不足,无法计算
6.如图所示,在□ABCD中,对角线AC,BD相交于点O,且OA=OB,∠OAD=65°.则∠ODC= 25° .
7.如图所示,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连结AE,BF.当∠ACB= 60° 时,四边形ABFE为矩形.
8.在平面直角坐标系中,有A(﹣2,﹣2),B(2,2),C(0,4)三个点,当点D的坐标为 (﹣4,0) 时,四边形ABCD是矩形.
9.如图所示,在□中,对角线AC与BD交于点O,OM⊥BC于点M,且BM=CM.
求证:□是矩形.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
又∵OM⊥BC,BM=CM,∴OB=OC.
∴AC=BD.∴□ABCD是矩形.
10.如图所示,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:
(1)△ABE≌△ACD.
(2)四边形BCDE是矩形.
(1)∵∠BAD=∠CAE,∴∠EAB=∠DAC.
在△ABE和△ACD中,∵∴△ABE≌△ACD(SAS).
(2)∵△ABE≌△ACD,∴BE=CD,
∵DE=BC,∴四边形BCDE为平行四边形.
∵AB=AC,∴∠ABC=∠ACB.
∵△ABE≌△ACD,∴∠ABE=∠ACD.∴∠EBC=∠DCB.
∵四边形BCDE为平行四边形,∴EB∥DC.
∴∠EBC+∠DCB=180°.∴∠EBC=∠DCB=90°.
∴四边形BCDE是矩形.
【能力提升培优】
11.平行四边形内角平分线能够围成的四边形是( B )
A.
梯形
B.
矩形
C.
正方形
D.
不是平行四边形
12.如图所示,在△ABC中,AC的中垂线交AC,AB于点D,F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( A )
A.
2
B.
2
C.
3
D.
3
13.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连结EF,则线段EF的最小值是( B )
A.
2.5
B.
2.4
C.
2.2
D.
2
14.如图所示,将□ABCD的边DC延长到点E,使CE=CD,连结AE交BC于点F,∠AFC=n∠D,当n= 2 时,四边形ABEC是矩形.
15.如图所示,已知□ABCD,给出下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC.其中能说明□ABCD是矩形的有(填写序号) ①④ .
16.如图所示,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF中点,则AM的取值范围是 ≤AM<6 .
17.如图所示,在△ABC中,O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
(1)∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6.∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.∴OE=OF.
(2)如图所示,∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,∴EF==13.
∴OC=EF=.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO.
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴□AECF是矩形.
18.如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA的延长线于点E,PF⊥AC交AC的延长线于点F.
(1)求证:四边形AEPF是矩形.
(2)D为BC中点,连结DE,DF.求证:DE=DF.
(1)∵∠BAC=90°,PE⊥AB,PF⊥AC.
∴四边形AEPF是矩形.
(2)连结DA.∵∠BAC=90°,AB=AC,D为BC中点,
∴DA=DC,∠DAE=∠DCF=135°.
又由(1)知AE=PF,△CFP是等腰直角三角形,
∴CF=PF=AE.∴△DAE≌△DCF.∴DE=DF.
【中考实战演练】
19.【临沂】如图所示,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( B )
A.
AB=BE
B.
DE⊥DC
C.
∠ADB=90°
D.
CE⊥DE
20.【内江】如图所示,将□ABCD的边AB延长至点E,使AB=BE,连结DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC.
(2)连结BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
(1)在□ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,∴BE=DC.
∴四边形BECD为平行四边形.∴BD=EC.
在△ABD与△BEC中,∵∴△ABD≌△BEC.
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC.∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.∴□BECD为矩形.
【开放应用探究】
21.已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,易证得结论PA2+PC2=PB2+PD2,请你探究:当点P分别在图2、图3中的位置时,PA2,PB2,PC2和PD2又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图2证明你的结论.
对图2的探究结论为 ;对图3的探究结论为 ;
结论均是PA2+PC2=PB2+PD2.
证明:如图所示,过点P作MN∥AB,交AD于点M,交BC于点N.
∴四边形ABNM和四边形NCDM均为矩形,
根据(1)中的结论可得,在矩形ABNM中有PA2+PN2=PB2+PM2,在矩形NCDM中有PC2+PM2=PD2+PN2,
两式相加得PA2+PN2+PC2+PM2=PB2+PM2+PD2+PN2,
∴PA2+PC2=PB2+PD2.
5.2 菱形(1)
重点提示:(1)菱形的定义:有一组邻边相等的平行四边形是菱形.(2)菱形的性质:菱形是特殊的平行四边形,它具有平行四边形的所有性质,菱形的四条边都相等,菱形的对角线互相垂直且每条对角线平分一组对角.(3)菱形既是中心对称图形又是轴对称图形,对角线所在直线是它的对称轴.
【夯实基础巩固】
1.菱形具有而平行四边形不具有的性质是( D )
A.
两组对边分别平行
B.
两组对角分别相等
C.
对角线互相平分
D.
对角线互相垂直
2.如图所示,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( D )
A.
10
B.
C.
6
D.
5
3.如图所示,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( B )
A.
18
B.
18
C.
36
D.
36
4.如图所示,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E,F,连结EF,则△AEF的面积是( B )
A.
4
B.
3
C.
2
D.
5.一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( C )
A.
3:1
B.
4:1
C.
5:1
D.
6:1
6.如图所示,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 (4,4) .
7.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 .
8.如图所示,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于点H,连结OH,则∠DHO= 25° .
9.如图所示,在菱形ABCD中,AE⊥BC,点E为垂足,且BE=CE,AB=2.求:
(1)∠BAD的度数.
(2)对角线AC的长及菱形ABCD的周长.
(1)∵在菱形ABCD中,AE⊥BC,且BE=CE,∴△ABC为等边三角形 ,∠ B=∠D=60°.
∴∠BAD=∠BCD=120°.
(2)AC=AB=2,菱形ABCD的周长为4×2=8.
10.如图所示,菱形ABCD的对角线AC,BD相交于点O,E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论.
(2)若AB=13,AC=10,求线段EF的长.
(1)△OEF是等腰三角形.
证明:∵四边形ABCD是菱形,
∴AB=AD,OA=OC,OB=OD.
∵点E,F分别是边AB,AD的中点,
∴EO=AB,OF=AD.
∴EO=FO,∴△OEF是等腰三角形.
(2)∵四边形ABCD是菱形,AC=10,
∴AO=5,∠AOB=90°,∴BO==12.∴BD=24.
∵点E,F分别是边AB,AD的中点,
∴EF=BD=12.
【能力提升培优】
11.如图所示,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于( A )
A. B. C.12 D.24
12.如图所示,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC等于( C )
A.
35°
B.
45°
C.
50°
D.
55°
13.如图所示,3个全等的菱形按如图所示方式拼合在一起,恰好得到一个边长相等的六边形,则菱形较长的对角线与较短的对角线之比是( A )
A.
B.
C.
2
D.
14.如图所示,在菱形ABCD中,点E是AB上的一点,连结DE交AC于点O,连结BO,且∠AED=50°,则∠CBO= 50° .
15.如图所示,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作点P到直线AB,AD的垂线段PE,PF,则PE+PF= 3 .
16.如图所示,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8﹣8,则菱形ABCD的边长为 2 .
17.如图所示,在菱形ABCD中,对角线AC,BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为矩形.
(2)在BC上截取CF=CO,连结OF,若AC=8,BD=6,求四边形OFCD的面积.
(1)∵DE∥AC,CE∥BD,∴四边形OCED为平行四边形.
∵四边形ABCD是菱形,∴AC⊥BD.∴∠DOC=90°.
∴四边形OCED为矩形.
(2)∵四边形ABCD是菱形,∴AC与BD互相垂直平分于点O.
∴OD=OB=BD=3,OA=OC=AC=4.
∴S△DOC=6.
在Rt△OBC中,BC==5,CF=OC=4.
∴S△OCF=.∴S四边形OFCD=S△DOC+S△OCF=6+=.
18.如图所示,在菱形ABCD中,∠B=60°,点E,F分别在边BC,CD上.
(1)若AB=4,试求菱形ABCD的面积.
(2)若∠AEF=60°,求证:AB=CE+CF.
(1)在菱形ABCD中,AB=BC,
∵∠B=60°,∴△ABC是等边三角形.
∵AB=4,∴等边三角形ABC底边BC上的高为4×=2.
∴菱形ABCD的面积=4×2=8.
(2)如图所示,将△AEC绕点A顺时针旋转60°得到△AE′B,则△AEE′为等边三角形,∴∠AE′E=60°.
∵∠AEF=60°,∴∠CEF=∠AEC﹣∠AEF=∠AEC﹣60°.
又∵∠BE′E=∠AE′B﹣∠AE′E=∠AE′B﹣60°,∴∠BE′E=∠CEF.
∵∠B=60°,菱形的对边AB∥CD,∴∠ECF=180°﹣60°=120°.
又∵∠E′BE=∠ABC+∠ABE′=∠ABC+∠ACB=60°+60°=120°,
∴∠E′BE=∠ECF.∴△EE′B≌△FEC(ASA).∴BE=CF.
∴BC=CE+BE=CE+CF.∵AB=BC,∴AB=CE+CF.
【中考实战演练】
19.【本溪】如图所示,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
20.【安徽】如图所示,在矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A.
2
B.
3
C.
5
D.
6
【开放应用探究】
21.有一种汽车用“千斤顶”,它由4根连杆组成菱形ABCD,当螺旋装置顺时针旋转时,B,D两点的距离变小,从而顶起汽车.若AB=30,螺旋装置每顺时针旋转1圈,BD的长就减少1.设BD=a,AC=h.
(1)当a=40时,求h值.
(2)从a=40开始,设螺旋装置顺时针旋转x圈,求h关于x的函数表达式.
(3)从a=40开始,螺旋装置顺时针连续旋转2圈,设第1圈使“千斤顶”增高s1,第2圈使“千斤顶”增高s2,试判定s1与s2的大小,并说明理由.若将条件“从a=40开始”改为“从某一时刻开始”,则结果如何,为什么?
(1)连结AC交BD于点O.
∵四边形ABCD为菱形,a=40,∴∠AOB=90°,OA=,OB=20.
在Rt△AOB中,
∵AO+BO=AB,即,∴h=20.
(2)从a=40开始,螺旋装置顺时针旋转x圈,则BD=40﹣x,
∴.∴h=.
(3)s1>s2.理由如下:
在h=中,
令x=0得,h0=≈44.721;
令x=1得,h1=≈45.596;
令x=2得,h2=≈46.433;
∴s1=h1﹣h0≈0.88,s2=h2﹣h1≈0.84.∴s1>s2.
若将条件“从a=40开始”改为“从任意时刻开始”,则结论s1>s2仍成立.
∵,
而2a﹣1>2a﹣3,,
∴s1>s2.
5.2 菱形(2)
重点提示:判定一个四边形是菱形有三种方法:(1)一组邻边相等的平行四边形是菱形.(2)四条边相等的四边形是菱形.(3)对角线互相垂直的平行四边形是菱形.注意方法(1)和(3)要先利用平行四边形的判定方法证明四边形是平行四边形.
【夯实基础巩固】
1.如图所示,要使□ABCD成为菱形,则需添加的一个条件是( B )
A.
AC=AD
B.
BA=BC
C.
∠ABC=90°
D.
AC=BD
2.如图所示,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据他的作图方法可知,四边形ADBC一定是( B )
A.
矩形
B.
菱形
C.
正方形
D.
梯形
3.如图所示,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是( A )
A.
AB=BC
B.
AC=BC
C.
∠B=60°
D.
∠ACB=60°
4.下列说法中正确的是( A )
A.
四边相等的四边形是菱形
B.
一组对边相等,另一组对边平行的四边形是菱形
C.
对角线互相垂直的四边形是菱形
D.
对角线互相平分的四边形是菱形
5.如图所示是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
对于甲、乙两人的作法,可判断( C )
A.
甲正确,乙错误
B.
甲错误,乙正确
C.
甲、乙均正确
D.
甲、乙均错误
6.如图所示,在□ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,请添加一个条件: AE=EC(答案不唯一) ,使四边形AECF为菱形.
7.如图所示,矩形ABCD的对角线AC,BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长为 16 .
8.如图所示,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,且AD交EF于点O,则∠AOF= 90° .
9.如图所示,CE是△ABC的外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
∵AF∥CD,FG∥AC,
∴四边形ACGF是平行四边形,∠FCG=∠AFC.
∵CE平分∠ACD,∴∠ACF=∠GCF.∴∠ACF=∠AFC.
∴AC=AF.∴四边形ACGF是菱形.
10.如图所示,在△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连结BD,CE交于点F.求证:
(1)△ABD≌△ACE.
(2)四边形ABFE是菱形.
(1)由旋转可知∠DAE =∠BAC =40°,∴∠BAD=∠CAE=100°.
∵AB=AC,∴AB=AC=AD=AE.
∴△ABD≌△ACE(SAS).
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°.
∴∠BAE=∠BFE.∴四边形ABFE是平行四边形.
∵AB=AE,∴□ABFE是菱形.
【能力提升培优】
11.如图所示,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,这个条件可以是( D )
A.
AB//CD
B.
AC⊥BD
C.
AC=BD
D.
AD=BC
12.如图所示,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以cm/s的速度向终点A运动;同时,动点Q从点C出发沿CB方向以1cm/s的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t(s),若四边形QPBP′为菱形,则t的值为( B )
A.
B.
2
C.
2
D.
4
13.如图所示,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF交AC于点M,连结DE,BO.若∠COB=60°,FO=FC,给出下列结论:
①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2.
其中正确结论的个数有( C )
A.
1个
B.
2个
C.
3个
D.
4个
14.如图所示,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD,CB为边作□CDEB,当AD= ,□CDEB为菱形.
15.如图所示,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连结BG,DF.若FG=5,CF=6,则四边形BDFG的面积为 15 .
16.如图所示,在四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBnCnDn.下列结论中正确的有 ②③④ .
①四边形A2B2C2D2是矩形; ②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长为; ④四边形AnBnCnDn的面积是.
17.如图1所示,在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠DCE=90°,AB与CE交于点F,ED与AB,BC,分别交于点M,H.
(1)求证:CF=CH.
(2)如图2所示,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形,并证明你的结论.
(1)∵AC=CE=CB=CD,∠ACB=∠ECD=90°,
∴∠A=∠B=∠D=∠E=45°.
在△BCF和△ECH中,∵
∴△BCF≌△ECH(ASA).∴CF=CH.
(2)四边形ACDM是菱形.
证明:∵∠ACB=∠DCE=90°,∠BCE=45°,∴∠ACE=∠BCD=45°.
∵∠E=45°,∴∠ACE=∠E.
∴AC∥DE.∴∠AMH=180°﹣∠A=135°=∠ACD.
又∵∠A=∠D=45°,
∴四边形ACDM是平行四边形.
∵AC=CD,∴四边形ACDM是菱形.
18.如图所示,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连结DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
(3)在(2)的条件下,试确定点E的位置,使得∠EFD=∠BCD,并说明理由.
(1)在△ABC和△ADC中,∵
∴△ABC≌△ADC(SSS).∴∠BAC=∠DAC.
在△ABF和△ADF中,∵
∴△ABF≌△ADF(SAS).∴∠AFD=∠AFB.
∵∠AFB=∠CFE,∴∠AFD=∠CFE.
(2)∵AB∥CD,∴∠BAC=∠ACD.
∵∠BAC=∠DAC,∴∠CAD=∠ACD.∴AD=CD.
∵AB=AD,CB=CD,∴AB=CB=CD=AD.
∴四边形ABCD是菱形.
(3)当EB⊥CD时,∠EFD=∠BCD.理由如下:
∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF.
在△BCF和△DCF中,∵
∴△BCF≌△DCF(SAS).∴∠CBF=∠CDF.
∵BE⊥CD,∴∠BEC=∠DEF=90°.
∴∠BCD+∠CBE=∠CDF+∠EFD.∴∠EFD=∠BCD.
【中考实战演练】
19.【曲靖】如图所示,在矩形ABCD中,E,F分别是AD,BC中点,连结AF,BE,CE,DF分别交于点M,N,四边形EMFN是( B )
A.
正方形
B.
菱形
C.
矩形
D.
无法确定
20.【荆门】如图所示,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.
∵AB∥CD,∴∠DCA=∠BAC.
∵DF∥BE,∴∠DFA=∠BEC.∴∠AEB=∠CFD.
在△AEB和△CFD中,∵
∴△AEB≌△CFD(ASA).∴AB=CD.
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AC平分∠BAD,∴∠BAE=∠DAF.
∵∠BAE=∠DCF,∴∠DAF=∠DCF.
∴AD=CD.∴四边形ABCD是菱形.
【开放应用探究】
21.如图1所示,P是线段AB上一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连结CD,点E,F,G,H分别是AC,AB,BD,CD的中点,顺次连结E,F,G,H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由.
(2)当点P在线段AB的上方时,如图2所示,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由.
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,不必说明理由.
(1)四边形EFGH是菱形. (2)成立.理由如下:
如图1所示,连结AD,BC. ∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB.
又∵PA=PC,PD=PB,∴△APD≌△CPB.∴AD=CB.
∵E,F,G,H分别是AC,AB,BD,CD的中点,
∴EF,FG,GH,EH分别是△ABC,△ABD,△BCD,△ACD的中位线.
∴EF=BC,FG=AD,GH=BC,EH=AD.
∴EF=FG=GH=EH.∴四边形EFGH是菱形.
(3)如图2所示,四边形EFGH是正方形.
5.3 正方形(1)
重点提示:判定一个四边形是正方形的方法一般有两种:一是先判定这个四边形是矩形,再说明它的邻边相等或对角线互相垂直;二是先判定这个四边形是菱形,再说明它有一个角是直角或对角线相等.
【夯实基础巩固】
1.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( C )
A.
平行四边形
B.
菱形
C.
正方形
D.
矩形
2.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是( D )
A.
AO=CO
B.
AO=CO=BO=DO
C.
AO=CO,BO=DO,AC⊥BD
D.
AO=BO=CO=DO,AC⊥BD
3.如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( D )个正方形.
A.
0
B.
1
C.
2
D.
3
4.甲、乙、丙、丁四位同学到工厂实习,工人师傅拿一把尺子要他们帮助检测一个四边形构件是否为正方形,他们各自做了如下检测:
甲量得构件四边都相等;
乙量得构件的两条对角线相等;
丙量得构件的一组邻边相等;
丁量得构件的四边相等且两条对角线也相等.
检测后,他们都说是正方形,你认为说得最有把握的是( D )
A.
甲
B.
乙
C.
丙
D.
丁
5.如图所示,将长方形纸片折叠,使点A落BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( A )
A.
邻边相等的矩形是正方形
B.
对角线相等的菱形是正方形
C.
两个全等的直角三角形构成正方形
D.
轴对称图形是正方形
6.如果一个四边形既是菱形又是矩形,那么它一定是 正方形 .
7.如图所示,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB:AD= 1:2 时,四边形MENF是正方形.
8.如图所示,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件 ∠ABC=90° 时,四边形BEDF是正方形.
9.如图所示,在矩形ABCD中,∠ABC的平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别为点E,F.判定四边形EBFM的形状,并证明你的结论.
四边形EBFM是正方形.
证明:∵四边形ABCD为矩形,∴∠ABC=90°.
∵MF⊥BC,ME⊥AB,∴∠BFM=∠MEB=90°.
∵∠ABC=∠BFM=∠MEB=90°,∴四边形EBFM为矩形.
∵BM平分∠ABC,∴ME=MF.∴四边形EBFM为正方形.
10.如图所示,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)求证:DE=DF.
(2)只添加一个条件,使四边形EDFA是正方形,请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明)
(1)∵AB=AC,∴∠B=∠C.∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.又∵D是BC的中点,∴BD=CD.∴△DEB≌△DFC.故DE=DF.
(2)略
【能力提升培优】
11.如图所示,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕所成角的度数为( C )
A.
22.5°
B.
30°
C.
45°
D.
60°
12.如图所示,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( B )
A.
30
B.
34
C.
36
D.
40
13.如图所示,在一张3×3的方格纸上,若以格点(即小正方形的顶点)为顶点画正方形,则在该3×3方格纸上最多可画出的正方形的个数是( D )
A.
13
B.
14
C.
18
D.
20
14.如图所示,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,则∠ACB= 90 度时,四边形AECF是正方形.
15.如图所示,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是 3 .
16.菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形就越接近正方形.
①当菱形的一个内角为70°时,“接近度”= .
②当菱形的“接近度”= 时,菱形就是正方形.
(2)若我们将菱形的“接近度”定义为(m<n),则:
①当菱形的一个内角为60°时,“接近度”= .
②当菱形的“接近度”= 时,菱形就是正方形.
(3)甲、乙两位同学仿照菱形的“接近度”的定义,给出了如下两种矩形的“接近度”的定义,在你认为合理的定义后面打“√”,不合理的打“×”.
①甲:设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a-b|,于是|a-b|越小,矩形越接近于正方形. ( ) ②乙:设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为,于是越小,矩形越接近于正方形. ( )
16.(1)①40 ②0 (2)① ②1 (3)①× ②√
17.如图所示,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连结CF.
(1)求证:D是BC的中点.
(2)如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论.
(3)当△ABC满足什么条件时,四边形ADCF为正方形?并证明你的结论.
(1)∵AF=DC,AF∥BC,∴四边形ADCF为平行四边形.∴AF=CD.
∵E为AD的中点,AF∥BD,∴AE=DE,∠AFE=∠DBE.
在△AEF和△DEB中,∵∴△AEF≌△DEB(AAS).
∴BD=AF.∴BD=CD,即D为BC的中点.
(2)四边形ADCF为矩形.理由如下:
连结AB.∵AB=AC,D为BC的中点,
∴AD⊥BC.∴∠ADC=90°.∴□ADCF为矩形.
(3)当△ABC为等腰直角三角形时,四边形ADCF为正方形.理由如下:
∵△ABC为等腰直角三角形,D为BC中点,
∴AD⊥BC,AD=BC=BD=CD.
∴矩形ADCF为正方形.
18.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图1所示),CE=2cm,将长方形ABCD绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.
(1)当旋转到顶点D,H重合时,连结AG(如图2所示),求点D到AG的距离.
(2)当α=45°时(如图3所示),求证:四边形MHND为正方形.
(1)作DK⊥AG于点K.
∵CD=CE=DE=2cm,∴△CDE是等边三角形.
∴∠CDE=60°.∴∠ADG=360°﹣2×90°﹣60°=120°.
∵AD=DG=1cm,∴∠DAG=∠DGA=30°.∴DK=DG=cm,
∴点D到AG的距离为cm.
(2)∵α=45°,∴∠NCE=∠NEC=45°.∴CN=NE.
∴∠CNE=90°.∴∠DNH=90°.
∵∠D=∠H=90°,∴四边形MHND是矩形.
∵CN=NE,∴DN=NH.∴矩形MHND是正方形.
【中考实战演练】
19.【日照】小明在学习了正方形之后,给同桌小文出了道题:下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD,请你从中选两个作为补充条件,使□ABCD为正方形(如图所示).现有下列四种选法,你认为其中错误的是( B )
A.
①②
B.
②③
C.
①③
D.
②④
20.如图所示,AB垂直平分CD,并交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为点E,F.
(1)求证:∠CAB=∠DAB.
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
(1)∵AB是CD的垂直平分线,∴AC=AD.
∵AB⊥CD,∴∠CAB=∠DAB.
(2)∵ME⊥A C,MF⊥AD,∠CAD=90°,即∠CAD=∠AEM=∠AFM=90°,
∴四边形AEMF是矩形.
又∵∠CAB=∠DAB,ME⊥A C,MF⊥AD,
∴ME=MF.∴矩形AEMF是正方形.
【开放应用探究】
21.以四边形ABCD的边AB,BC,CD,DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连结这四个点,得四边形EFGH.
(1)如图1所示,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2所示,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图3所示,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE.
②求证:HE=HG.
③四边形EFGH是什么四边形?请说明理由.
(1)四边形EFGH的形状是正方形.
(2)①∵在□ABCD中,AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣α.
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°.
∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣(180°﹣α)=90°+α.
②∵△AEB和△DGC是等腰直角三角形,
∴AE=AB,DG=CD.
∵在□ABCD中,AB=CD,∴AE=DG.
∵△AHD和△DGC是等腰直角三角形,∴∠HDA=∠CDG=45°.
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE.
∵△AHD是等腰直角三角形,∴HA=HD.
∴△HAE≌△HDG.∴HE=HG.
③四边形EFGH是正方形,理由如下:
由②同理可得GH=GF,FG=FE.
∵HE=HG,∴GH=GF=EF=HE.
∴四边形EFGH是菱形.
∵△HAE≌△HDG,∴∠DHG=∠AHE.
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°.
∴四边形EFGH是正方形.
5.3 正方形(2)
重点提示:正方形是最特殊的四边形,它综合了平行四边形、矩形和菱形的所有性质,正方形的四条都相等,四个角都是直角,对角线互相垂直平分并且相等,其对角线可以将正方形分成大小不同的八个等腰直角三角形.
【夯实基础巩固】
1.正方形具有而菱形不一定具有的性质是( D )
A.
四条边相等
B.
对角线互相垂直平分
C.
对角线平分一组对角
D.
对角线相等
2.若正方形的周长为40,则其对角线长为( C )
A.
100
B.
C.
D.
10
3.如图所示,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( D )
A.
45°
B.
55°
C.
60°
D.
75°
4.如图所示,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为( C )
A.
20°
B.
25°
C.
35°
D.
40°
5.如图所示,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( B )
A.n B.n﹣1 C. D.n
6.如图所示,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 5 .
7.如图所示,在正方形ABCD外侧,作等边三角形ADE,连结AC,BE相交于点F,则∠BFC= 60 度.
8.如图所示,边长为8的正方形ABCD中,M是BC上的一点,连结AM,作AM的垂直平分线GH交AB于点G,交CD于点H,若CM=2,则GH= 10 .
9.如图所示,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连结BE,DF,DF交对角线AC于点P,且DE=DP.求证:
(1)AE=CP.
(2)BE∥DF.
(1)∵DE=DP,∴∠DEP=∠DPE.
∴∠AED=∠CPD.
∵四边形ABCD是正方形,
∴AD=CD=BC,∠DAC=∠BCE=∠DCA=45°.
∴△ADE≌△CDP(AAS).∴AE=CP.
(2)在△BCE和△DCE中,∵
∴△BCE≌△DCE (SAS).∴∠BEC=∠DEP.
∴∠BEC=∠DPE.∴BE∥DF.
10.如图所示,在正方形ABCD中,点E在BC的延长线上,AE分别交DC,BD于点F,G, H为EF的中点.求证:
(1)∠DAG=∠DCG.
(2)GC⊥CH.
(1)∵四边形ABCD为正方形,∴AD=DC,∠ADB=∠CDB=45°.
∵DG=DG,∴△ADG≌△CDG.∴∠DAG=∠DCG.
(2)∵四边形ABCD为正方形,∴AD∥BE,
∴∠DAG=∠E.∵∠DAG=∠DCG,∴∠E=∠DCG.
∵H为Rt△CEF斜边EF边的中点,∴CH=HE=EF.
∴∠HCE=∠E,∴∠DCG=∠HCE.
∵∠FCH+∠HCE=90°,
∴∠FCH+∠DCG=90°,即∠GCH=90°.∴GC⊥CH.
【能力提升培优】
11.如图所示,在正方形ABCD中,对角线AC,BD相交于O,AB=2,E是BC中点,点P在对角线AC上滑动,则BP+EP的最小值是( C )
A.
B.
2
C.
D.
3
12.如图所示,在正方形ABCD中,E,F分别是边CD,AD上的点,且CE=DF,AE与BF相交于点O,则下列结论中错误的是( C )
A.
AE=BF
B.
AE⊥BF
C.
AO=OE
D.
S△AOB=S四边形DEOF
13.如图所示,在正方形ABCD中,AD=5,E,F是正方形ABCD内两点,且AE=CF=3,BE=DF=4,则EF的长为( D )
A. B. C. D.
14.如图所示,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点,已知四边形ABCD是正方形,则k的值为 .
15.如图所示,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
16.如图所示,四边形ABCD是正方形,E是CF上一点,若四边形DBEF是菱形,则∠EBC= 15° .
【解析】过点D作DG⊥CF于点G.设正方形ABCD的边长为1,则由勾股定理可得BD=.
∵四边形ABCD为正方形,四边形DBEF为菱形,∴DF=BD=,∠DCG=∠CDB=45°.
∵DG⊥CF,∴△CDG为等腰直角三角形.∴DG=.∴在Rt△DFG中,DF=2DG.∴∠F=30°.∴∠DBE=∠F=30°.∴∠EBC=45°-30°=15°.
17.如图所示,G是正方形ABCD的对角线CA延长线上的任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD.
(2)若AB=3,AG=3,求EB的长.
(1)∵四边形ABCD,AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG.
∴∠EAB=∠GAD.∴△EAB≌△GAD(SAS).
(2)∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD=AB=6.
∴∠DOG=90°,OA=OD=BD=3.
∵AG=3,∴OG=OA+AG=6.
∴GD=.∴EB=.
18.如图1所示,在正方形ABCD中,E为BC上一点,过点B作BG⊥AE于点G,延长BG至点F,使∠CFB=45°.
(1)求证:AG=FG.
(2)如图2所示,延长FC,AE交于点M,连结DF,BM,若C为FM中点,BM=10,求FD的长.
(1)如图1所示,过点C作CH⊥BF于点H.
∵∠CFB=45°,∴CH=HF.
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,∴∠BAG=∠FBE.
∵AG⊥BF,CH⊥BF,∴∠AGB=∠BHC=90°.
又∵四边形ABCD为正方形,∴AB=BC.
∴△AGB≌△BHC.∴AG=BH,BG=CH.
∵BH=BG+GH,∴BH=CH+GH=HF+GH=FG.∴AG=FG.
(2)如图2所示,过点C作CH⊥BF于点H,过点B作BK⊥CM于K,过点D作DQ⊥MF交MF延长线于Q.
∵CH⊥GF,∴CH∥GM.
∵C为FM的中点,∴CH=GM.∴BG=GM.
∵BM=10,∴BG=2,GM=4.
∴AG=4,AB=10.∴HF=2.∴CF=2×=2.∴CM=2.
∵CK=CM=CF=,∴BK=3.∴△BKC≌△CQD.
∴CQ=BK=3,DQ=CK=.
∴QF=3﹣2=,∴DF==2.
【中考实战演练】
19.如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连结EF.给出下列结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,其中正确的结论个数有( B ).
A.
5个
B.
4个
C.
3个
D.
2个
20.【黄冈】如图所示,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED= 65 度.
【开放应用探究】
21.如图所示,在正方形ABCD中,AC,BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
(1)若点E在图1的位置,判断OE与OF的数量关系,并证明你的结论.
(2)若点E在AC的延长线上,请在图2中按题目要求补全图形,判断OE与OF的数量关系,并证明你的结论.
(1)OE=OF.理由如下:
∵在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°,
∴∠OBE+∠BEO=90°.
∵AH⊥EB,∴∠AHE=90°.
∴∠HAE+∠AEH=90°.∴∠OBE=∠OAF.
∴△AOF≌△BOE(ASA).∴OE=OF.
(2)OE=OF仍然成立.理由如下:
如图所示,∵在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°,
∴∠FAO+∠F=90°.
∵AH⊥EB,∴∠AHE=90°.
∴∠HAE+∠E=90°.∴∠E=∠F.
∴△AOF≌△BOE(AAS).∴OE=OF.
∴结论仍然成立.
专题复习一 方程思想与几何计算
重点提示:方程思想是数学重要思想方法,在几何计算中,当直接计算有困难时,列方程解决问题是重要思路,常用于列方程的等量关系有三角形(多边形)的内角和定理、勾股定理等.
【夯实基础巩固】
菱形的周长为20cm,两邻角的比为1:3,则菱形的面积为( C )
A.25cm2 B.16cm2 C.cm2 D.cm2
2.已知菱形的周长为40,两条对角线之比3:4,则菱形面积为( D )
A.
12
B.
24
C.
48
D.
96
3.如图所示,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF为( A )
A.
6.5dm
B.
6dm
C.
5.5dm
D.
4dm
4.如图所示,在菱形ABCD中,E,F分别是边AB和BC的中点,EP⊥CD于点P,设∠A=x°,则∠FPC的度数为( D )
A.° B.° C.° D.°
5.如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( A )
A.
3cm
B.
4cm
C.
5cm
D.
6cm
6.如图所示,在矩形ABCD中,两个小正方形的面积分别为S1,S2.若S1=4,S2=16,则图中阴影部分面积为 4 .
7.如图所示,在矩形ABCD中,AB=7cm,BC=cm,点P从点A出发以1cm/s的速度移动到点B.点P出发 s后,PA=2PC.
8.如图所示,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 (10,3) .
9.如图所示,P是矩形ABCD内一点,若PA=3,PB=4,PC=5,则PD= 3 .
10.如图所示,等腰三角形CEF的两腰CE,CF的长与菱形ABCD的边长相等,点E,F分别在AB,AD上.
(1)求证:△BEC≌△DFC.
(2)当△ECF是等边三角形时,求∠B的度数.
(1)∵四边形ABCD是菱形.∴CB=CD,且∠B=∠D.
∵△CEF是等腰三角形,∴CE=CF.
∵CE=CB,CF=CD,∴∠B=∠CEB,∠D=∠CFD.
∴∠CEB=∠CFD.∴△BEC≌△DFC(AAS).
(2)设∠B=x.∵CE=CB,∴∠CEB=∠B=x.∴∠BCE=180﹣2x.
同理∠FCD=180﹣2x.
∵△CEF是等边三角形,∴∠ECF=60°.
∵四边形ABCD是菱形.∴∠B+∠BCD=180°.
∴x+2(180﹣2x)+60°=180°,解得x=80°.
∴∠B=80°.
【能力提升培优】
11.已知正方形ABCD的边长是10cm,△APQ是等边三角形,点P在BC上,点Q在CD上,则BP等于( C )
A.cm B.cm
C.cm D. cm
12.如图所示,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4,则FD的长为( B )
A.
2
B.
4
C.
D.
2
13.如图所示,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速运动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t s△DEF为等边三角形,则t的值为 .
14.正方形OA1B1C1,A1A2B2C2,A2A3B3C3按如图所示放置,其中点A1,A2,A3在x轴的正半轴上,点B1,B2,B3在直线y=﹣x+2上,则点A3的坐标为 .
15.如图所示,矩形ABCD被分成四部分,其中△ABE,△ECF,△ADF的面积分别为2,3,4,则△AEF的面积为 7 .
【解析】设AB=x,BC=y.∵,∴BE=.
∴EC=.∵,∴FC=.
∴DF=.∴.
化简得,即,解得xy=2(舍去)或xy=16.
∴.
16.如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/s的速度运动,点Q从点C开始沿CB边向点B以2cm/s的速度运动,如果点P,Q分别从点A,C同时出发,设运动时间为t(s).求:
(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
(1)由题意知AP=t cm,CQ=2t cm,∴BQ=(21﹣2t)cm.
∵AD∥BC,∴AP∥BQ.
又∵∠B=90°,∴要使四边形ABQP为矩形,只需满足AP=BQ,即t=21﹣2t,解得t=7.
∴当t=7时,四边形ABQP为矩形.
(2)由题意知AP=t cm,QC=2t cm,PD=(18﹣t)cm,当PD=QC时,四边形PACD为平行四边形,
即18﹣t=2t,解得t=6.
∴当t=6时,四边形PQCD为平行四边形.
17.如图所示,在矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF,BF.
(1)若DG=2,求证:四边形EFGH为正方形.
(2)若AE=x,求△EBF的面积S关于x的函数表达式,并判断是否存在x,使△EBF的面积是△CGF面积的2倍?若存在,求出x的值;若不存在,请说明理由.
(1)∵四边形ABCD是矩形,∴∠D=∠A=90°.
∵四边形EFGH是菱形,∴HG=HE.
在Rt△HDG和Rt△AEH中,∵
∴Rt△HDG≌Rt△EAH(HL).
∴∠DHG=∠AEH.∴∠DHG+∠AHE=90°.
∴∠GHE=90°.∴菱形EFGH为正方形.
(2)如图所示,过点F作FM⊥AB交AB的延长线于点M,MF与DC的延长线交于点N,连结GE.
∴FN⊥CD.
∵CD∥AB,∴∠DGE=∠MEG.
∵GH∥EF,∴∠HGE=∠FEG.∴∠DGH=∠MEF.
∴Rt△HDG≌Rt△FME.
∴DH=MF.∴AH=2.∴DH=MF=4.
∵AE=x,∴BE=10﹣x.
∴S△EBF=BE?FM=2(10﹣x)=20﹣2x.
S关于x的函数表达式为S=20﹣2x.
同理可证Rt△AHE≌Rt△FNG,∴FN=AH=2.
∵AH=2,AE=x,∴HE=HG=.
∴DG=.
∴CG=10﹣.∴S△GCF=CG?FN=10﹣.
若△EBF的面积是△CGF面积2倍,则
20﹣2x=2(10﹣),整理得x2=x2﹣12,此方程无解,
∴不存在x,使△EBF的面积是△CGF面积的2倍.
【中考实战演练】
18.【安顺】如图所示,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( A )
A.
B.
C.
D.
6
19.【荆州】如图所示,在矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于点D,则点D的坐标为 (0,2.1) .
【开放应用探究】
20.如图所示,在正方形ABCD中,DE与HG相交于点O.
(1)如图1所示,若∠GOD=90°,①求证:DE=GH. ②连结EH,求证:GD+EH≥DE.
(2)如图2所示,若∠GOD=45°,AB=4,HG=2,求DE的长.
(1)①如图1所示,过点D作DM//GH交BC的延长线于点M,则四边形GDMH为平行四边形,∴GH=DM,GD=MH,GH∥DM,
∴∠GOD=∠MDE=90°.∴∠MDC+∠EDC=90°.
∵∠ADE+∠EDC=90°,∴∠MDC=∠ADE.
∴△ADE≌△CDM.∴DE=DM.∴DE=GH.
②连结EH,EM.∵DM=DE,∠EDM=90°,∴△EDM是等腰直角三角形.
∴EM=DM=GH=DE.
∵MH+EH≥EM,GD=MH,∴EH+GD≥EM.∴GD+EH≥DE.
(2)如图2所示,过点D作DN∥GH交BC于点N,则四边形GHND是平行四边形,
∴DN=HG,GD=HN.
∵∠C=90°,CD=AB=4,HG=DN=2,∴CN==2.
∴BN=BC﹣CN=4﹣2=2.
作∠ADM=∠CDN,DM交BA的延长线于点M,
∴△ADM≌△CDN.
∴AM=NC,∠ADM=∠CDN,DM=DN.
∵∠GOD=45°,∴∠EDN=45°.
∴∠ADE+∠CDN=45°.∴∠ADE+∠ADM=45°=∠MDE.
∴△MDE≌△NDE.
∴EM=EN,即AE+CN=EN.设AE=x,则BE=4﹣x,
在Rt△BEN中,由勾股定理得,解得x=.
∴DE=.
专题复习二 转化思想与特殊四边形问题
重点提示:在研究新问题或复杂问题时,常常把问题转化为已知的或比较简单的问题来解决,因此转化思想在几何证明和计算中是一个重要的数学思想.在解与特殊四边形有关的问题时,常常将问题转化为特殊三角形问题解决.
【夯实基础巩固】
1.如图所示,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE等于( C )
A.
20°
B.
25°
C.
30°
D.
35°
2.如图所示,矩形ABCD的周长为68,它被分成7个全等的矩形,则矩形ABCD的面积为( C )
A.
98
B.
196
C.
280
D.
284
3.如图所示,把矩形ABCD沿EF翻折,点B恰好落在AD边的点B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( D )
A.
12
B.
24
C.
12
D.
16
4.如图所示,P是正方形ABCD的边AB上一点(点P不与点A,B重合),连结PD并将线段PD绕点P顺时针旋转90°,得线段PE,连结BE,则∠CBE等于( C )
A.
75°
B.
60°
C.
45°
D.
30°
5.如图所示,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分的面积与四边形EMCN的面积之比为( C )
A.
4:3
B.
3:2
C.
14:9
D.
17:9
6.如图所示,矩形ABCD的面积是16,EF过矩形ABCD对角线的交点O,阴影部分的面积是 4 .
7.如图所示,正方形ABCD的周长为16cm,则矩形EFCH的周长是 8 cm.
8.如图所示,在菱形ABCD中,边AB的垂直平分线与对角线AC相交于点E,若∠ABC=140°,则∠EDC= 120° .
9.如图所示,在正方形ABCD中,点H在BC上,EF⊥AH交AB于点E,交AH于点G,交DC于点F.若AB=3,BH=1,求EF的长.
如图所示,作FM⊥AB于点M,则FM=AB=3.
∵∠1+∠3=∠2+∠3=90°,∴∠1=∠2.
又∵FM=AB,∴Rt△FME≌Rt△ABH.
∴.
10.在菱形ABCD中,O是对角线的交点,E是边CD的中点,点F在BC的延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形.
(2)连结DF,如果DF⊥CF,请你写出图中所有的等边三角形.
(1)∵四边形ABCD是菱形,∴BO=DO.
∵E是边CD的中点,∴OE是△BDC的中位线.
∴OEBC.
∵CF=BC,∴OE CF.
∴四边形OCFE是平行四边形.
(2)图中的等边三角形有:△OCE,△ECF,△ABC,△ADC.
【能力提升培优】
11.如图所示,E,F分别是矩形ABCD的边AD,BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为( C )
A.
15
B.
20
C.
35
D.
40
12.如图所示,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( B )
A. B. C. D.
13.在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连结AE,BE,FA⊥AE交DP于点F,连结BF,FC.给出下列结论:①△ABE≌△ADF;②FB=AB;③CF⊥DP;④FC=EF. 其中正确的结论有( D )
A.
①②④
B.
①③④
C.
①②③
D.
①②③④
14.已知正方形ABCD的边长为4,点E在直线CD上,CE=2,点P在边AC上,且PB⊥PE,则PC的长为 3 .
15.如图所示,正方形ABCD的AB边上有一点P,AD边上有一点Q,且PQ=BP+DQ,则∠QCP= 45° .
16.如图所示,P为正方形ABCD内一点,若PA:PB:PC=1:2:3,则∠APB= 135° .
17.如图所示,在菱形ABCD中,∠B=60°,点E,F分别在边BC,CD上.
(1)若AB=4,试求菱形ABCD的面积.
(2)若∠AEF=60°,求证:AB=CE+CF.
(1)∵在菱形ABCD中,∠B=60°,
∴△ABC是等边三角形.
∵AB=4,∴等边三角形ABC底边上的高为4×=2.
∴菱形ABCD的面积=4×2=8.
(2)如图所示,将△AEC绕点A顺时针旋转60°得到△AE′B,则△AEE′为等边三角形.∴∠AE′E=60°.
∵∠AEF=60°,∴∠CEF=∠AEC﹣∠AEF=∠AEC﹣60°.
∵∠BE′E=∠AE′B﹣∠AE′E=∠AE′B﹣60°,∴∠BE′E=∠CEF.
∵∠B=60°,∴∠ECF=180°﹣60°=120°.
∵∠E′BE=∠ABC+∠ABE′=∠ABC+∠ACB=60°+60°=120°,∴∠E′BE=∠ECF.
在△EE′B和△FEC中,∵∴△EE′B≌△FEC(ASA).
∴BE=CF.∴BC=CE+BE=CE+CF.
∵AB=BC,∴AB=CE+CF.
18.如图所示,AC是正方形ABCD的对角线,O是AC的中点,Q是AB上一点,连结CQ,DP⊥CQ于点E,交BC于点P,连结OP,OQ.求证:
(1)△BCQ≌△CDP.
(2)OP=OQ.
(1)∵四边形ABCD是正方形,∴∠QBC=∠PCD=90°,BC=CD. ∴∠2+∠3=90°.
又∵DP⊥CQ,∴∠2+∠1=90°.∴∠1=∠3. ∴△BCQ≌△CDP.
(2)如图所示,连结OB.
∵△BCQ≌△CDP,∴BQ=PC.
∵四边形ABCD是正方形,∴∠ABC=90°,AB=BC.
∵O是AC中点,∴BO=AC=CO,∠4=∠ABC=45°=∠PCO.
在△BOQ和△COP中,∵
∴△BOQ≌△COP.∴OQ=OP.
【中考实战演练】
19.如图所示,菱形ABCD和菱形ECGF的边长分别为3和4,若∠A=120°,则图中阴影部分的面积是 .
20.如图所示,在正方形ABCD外取一点E,连结AE,BE,DE.过点A作AE的垂线交DE于点P,连结BP.若AE=AP=1,PB=.给出下列结论:①△APD≌△AEB﹔②点B到直线AE的距离为﹔③EB⊥ED﹔④S△APD+S△APB=+.其中正确的结论有( A )
A.
①③④
B.
①②③
C.
②③④
D.
①②④
【开放应用探究】
21.(1)有这样一道习题:如图1所示,在□ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为 和 .
(2)如图2所示,点P为□ABCD内一点,过点P分别作AD,AB的平行线分别交□ABCD的四边于点E,F,G,H.已知S□BHPE=3,S□PFDG=5,则S△PAC= .
(3)如图3所示,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形的面积和为14,四边形ABCD的面积为11,求菱形EFGH的周长.
(1)□AEPH 和□PGCF 或□ABGH 和□EBCF 或□AEFD 和□HGCD.
(2)1
(3)∵①②③④四个平行四边形的面积和为14,
∴
∵四边形ABCD的面积为11,∴
∴
设菱形EFGH的边长为x.
∵菱形的一个内角为30°,∴菱形EFGH的高为.
∴,解得x=6.
∴菱形EFGH的周长为6×4=24.
第5章综合测评卷
一、选择题(每题3分,共30分)
1.正方形是轴对称图形,它的对称轴共有( D )
A.
1条
B.
2条
C.
3条
D.
4条
2.如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连结AE,CF,则四边形AECF是( C )
A.
梯形
B.
矩形
C.
菱形
D.
正方形
3.菱形的周长为16,且有一个内角为120°,则此菱形的面积为( B )
A.
4
B.
8
C.
10
D.
12
4.如图所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( C )
A.
14
B.
15
C.
16
D.
17
5.如图所示,已知四边形ABCD是菱形,过顶点D作DE⊥AD,交对角线AC于点E,若∠DAE=20°,则∠CDE的度数是( C )
A.
70°
B.
60°
C.
50°
D.
40°
6.用直尺和圆规作一个菱形,如图所示,能得到四边形ABCD是菱形的依据是( B )
A.
一组邻边相等的四边形是菱形
B.
四边相等的四边形是菱形
C.
对角线互相垂直的平行四边形是菱形
D.
每条对角线平分一组对角的平行四边形是菱形
7.如图所示,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( A )
A.
S1=S2
B.
S1<S2
C.
S1>S2
D.
无法确定
8.如图所示,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( D )
A.-1 B. C. D.
9.如图所示,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG于点E,CF⊥AG于点F,则AE﹣GF的值为( B )
A.1 B. C. D.
10.如图所示,在矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,则四边形PFCG的面积为( D )
A.
5
B.
6
C.
7
D.
8
【解析】如图所示,分别过点P作AD,AB的垂线MN,QR,与矩形ABCD的边分别交于点M,N,Q,R.设PM=x,PQ=y,则由题意可得PN=4-x,PR=6-y.
∵AH=CF=2,AE=CG=3,∴ ,
二、填空题(每题4分,共24分)
11.木工师傅做一个宽60cm,高80cm的矩形木框,为稳固起见,制作时需要在对角顶点间加一根木条,则木条的长为 100 cm.
12.如图所示,在矩形ABCD中,AB=6cm,BC=3cm,E是DC的中点,BF=FC,则四边形DBFE的面积为 6 cm2.
13.如图所示,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠E=__67.5°__.
14.如图所示,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连结BF,DF,则BE:CF的值为 .
15.如图所示,菱形ABCD的两条对角线分别长6和8,P是对角线AC上的一个动点,M,N分别是边AB,BC的中点,则PM+PN的最小值是 5 .
16.如图所示,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=2,则AB= 1+ .
三、解答题(共66分)
17.(6分)在正方形ABCD中,AC为对角线,E为AC上一点,连结EB,ED.求证:∠BEC=∠DEC.
∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA.
在△BEC与△DEC中,∵
∴△BEC≌△DEC(SAS).
∴∠BEC=∠DEC.
18.(8分)如图所示,已知菱形ABCD的对角线交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)若∠E=50° ,求∠BAO的度数.
(1)∵四边形ABCD为菱形,∴AB=CD,AB∥CD.
又∵BE=AB,∴四边形BECD是平行四边形.∴BD=EC.
(2)∵四边形BECD是平行四边形,∴BD∥CE.
∴∠ABO=∠E=50°.
∵在菱形ABCD中,AC⊥BD,∴∠BAO=90°-∠ABO=40°.
19.(8分)如图所示,在□ABCD中,点E,F分别在AB,AD延长线上,使得EF∥BD,连结EF,分别交BC,CD于点P,Q,已知BE=BP.求证:
(1)∠E=∠F.
(2)□ABCD是菱形.
(1)∵BE=BP,∴∠E=∠BPE.
∵四边形ABCD是平行四边形,∴BC∥AD.
∴∠BPE=∠F.∴∠E=∠F.
(2)∵四边形ABCD是平行四边形,∴AB∥DC.∴∠DQF=∠E.
∵∠E=∠F,∠BPE=∠E,∴∠BPE=∠DQF.
∵EF∥BD,∴∠CBD=∠BPE,∠BDC=∠DQF.
∴∠CBD=∠CDB.∴BC=DC.∴□ABCD是菱形.
20.(10分)如图所示,在菱形ABCD中,F为BC边的中点,DF与对角线AC交于点M,过点M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长.
(2)求证AM=DF+ME.
(1)∵四边形ABCD是菱形,∴CB=CD,AB∥CD.∴∠1=∠ACD .
∵∠1=∠2 ,∴∠2=∠ACD .∴MC=MD .
∵ME⊥CD ,∴CD=2CE=2 .∴BC=CD=2.
(2) 延长DF,BA交于点G.
∵四边形ABCD是菱形,∴∠BCA=∠DCA .
∵BC=2CF,CD=2CE,∴CE=CF.
∵CM=CM,∴△CEM≌△CFM. ∴ME=MF.
∵AB∥CD,∴∠2=∠G, ∠GBF=∠BCD.
∵CF=BF,∴△CDF≌△BGF.∴DF=GF.
∵∠1=∠2, ∠G=∠2,∴∠1=∠G.
∴AM=GM=MF+GF=DF+ME.
21.(10分)已知△ABC和△DEF都是边长为10cm的等边三角形,且点B,C,D,E在同一直线上,连结AD,CF.若BD=3cm,△ABC沿着BE的方向以1cm/s的速度运动,设△ABC运动时间为t(s).
(1)当t为何值时,四边形ADFC是菱形.
(2)当t为何值时,四边形ADFC是矩形?并求其面积.
(3)当t为何值时,四边形ADFC的面积是100cm2?
(1)当t=3时,□ADFC是菱形.理由如下:
∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°.∴AC∥DF.
∴四边形ADFC是平行四边形.
当t=3时, B与D重合,∴AD=DF.∴四边形ADFC是菱形.
(2)当t=13时,四边形ADFC是矩形.理由如下:
此时B与E重合,∴AF=CD.又由(1)知四边形ADFC为平行四边形,∴□ADFC是矩形.
∴∠CFD=90°,CF=10cm.
∴S矩形ADFC=10×10=100(cm2).
(3)①B,D重合前,(7﹣t)×5÷2×2=100,解得t=﹣13(不合题意,舍去).
②B,D重合时,t=3,10×5÷2×2≠100(不合题意,舍去).
③B,D重合后,(t+7)×5÷2×2=100,解得t=13.
综上所述,当t为13时,□ADFC的面积是100cm2.
22.(12分)如图所示,∠MON=90°,在∠MON的内部有一个正方形AOCD,点A,C分别在射线OM,ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1.
(1)连结D1D,求证:∠D1DA=90°.
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论.
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1),(2)的结论,再做出一个合理的判断.
(1)∵∠D1AD+∠B1AD=90°,∠OAB1+∠B1AD=90°,
∴∠B1AO=∠D1AD.
∵AD1=AB1,AO=AD,
∴△OAB1≌△DAD1.∴∠D1DA=∠O=90°.
(2)猜想:∠C1CN=45°.
证明:如图1所示,连结C1C,作C1H⊥ON于点H,作C1G⊥CD1于点G,则有C1G=CH.
∵∠C1D1C+∠AD1D=90°,∠C1B1H+∠AB1O=90°,
∴∠C1D1C=∠C1B1H.
∵C1D1=B1C1,∠C1GD1=∠C1HB1=90°,
∴△C1GD1≌△C1 H B1.∴C1G=C1H.
又∵CH=C1G,∴△CHC1是等腰直角三角形.∴∠C1CN=45°.
(3)如图2所示,结论:∠ADD2=90°或∠C2CN=45°均可.
23.(12分)在平面直角坐标系中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC,BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.
(1)当∠BAO=45°时,求点P的坐标.
(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上.
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由.
(1)当∠BAO=45°时,∠PAO=90°,在Rt⊿AOB中,OA=AB=,在Rt⊿APB中,PA=AB=.
∴点P的坐标为.
(2)如图所示,过点P分别作x轴、y轴的垂线,垂足分别为M,N,则有
∠PMA=∠PNB=∠NPM=∠BPA=90°.
∴∠MPA=∠NPB.又PA=PB,
∴△PAM≌△PBN.∴PM=PN.
∴点P在∠AOB的平分线上.
(3)<h≤.当点B与点O重合时,点P到x轴的距离为,然后顶点A在x轴正半轴上向左运动,顶点B在y轴正半轴上向上运动时,点P到x轴的距离逐渐增大,当∠BAO=45°时,PA⊥x轴,这时点P到x轴的距离最大为,然后又逐渐减小到,∵x轴的正半轴、y轴的正半轴都不包含原点O ,∴点P到x轴的距离的取值范围是<h≤.
5.1 矩形(1)
重点提示:(1)矩形的定义:有一个角是直角的平行四边形.(2)矩形的性质:矩形是特殊的平行四边形,所以它具有平行四边形的所有性质,另外矩形的四个角都是直角、矩形的对角线相等.(3)矩形既是中心对称图形,也是轴对称图形,它有两条对称轴.
【夯实基础巩固】
1.如图所示,在矩形ABCD中,对角线AC,BD交于点O,下列说法中错误的是( D )
A.
∠ABC=90°
B.
AC=BD
C.
OA=OB
D.
OA=AD
2.如图所示,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断中错误的是( C )
A.
四边形ABCD由矩形变为平行四边形
B.
BD的长度增大
C.
四边形ABCD的面积不变
D.
四边形ABCD的周长不变
3.如图所示,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,若点A表示的数是﹣1,则对角线AC,BD的交点表示的数是( A )
A.
5.5
B.
5
C.
6
D.
6.5
4.如图所示,在矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=,则OE等于( A )
A.
1
B.
2
C.
3
D.
4
5.如图所示,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠EAO=15°,则∠BOE的度数为( C )
A.
85°
B.
80°
C.
75°
D.
70°
6.如图所示,在矩形ABCD中,点E为BC的中点,且∠AED=90°,AD=10,则AB的长为 5 .
7.如图所示,在矩形ABCD中,DE⊥AC,∠ADE=∠CDE,则∠BDC的度数为 30° .
8.如图所示,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是S1 = S2( 填“>”“<”或“=”)
9.如图所示,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为点E,F.
求证:BE=CF.
∵四边形ABCD为矩形,∴AC=BD,则BO=CO.
∵BE⊥AC于点E,CF⊥BD于点F,∴∠BEO=∠CFO=90°.
∵∠BOE=∠COF,∴△BOE≌△COF.∴BE=CF.
10.如图所示,在矩形ABCD中, F是CD中点,连结AF并延长交BC的延长线于点E,连结AC.
(1)求证:△ADF≌△ECF.
(2)若AB=1,BC=2,求四边形ACED的面积.
(1)∵F是CD中点,
∴DF=CF.
∵四边形ABCD是矩形,
∴AD∥BC,即AD∥CE.
∴∠ADF=∠ECF.
在△ADF和△ECF中,∵
∴△ADF≌△ECF(ASA).
(2)∵四边形ABCD是矩形,∴AD=BC=2,AB=CD=1,CD⊥AD.
由(1)知,△ADF≌△ECF,∴AD=CE.
∵AD∥CE,∴四边形ACED是平行四边形.
∴S四边形ACED =2×1=2.
【能力提升培优】
11. 如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( D )
A.
8
B.
8
C.
4
D.
6
12.如图所示,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于点H,且BH=DH,则DH的值是( C )
A. B. C. D.
13.如图所示,E是矩形ABCD内的一个动点,连结EA,EB,EC,ED,得到△EAB,△EBC,△ECD,△EDA,设它们的面积分别是m,n,p,q,给出下列结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则点E一定是AC与BD的交点;
④若m=n,则点E一定在BD上.
其中正确的结论有( B )
A.
①③
B.
②④
C.
①②③
D.
②③④
14.将一个含30°的角的直角三角尺按如图所示放置在矩形纸板上,∠AMF=90°,已知矩形纸板的长是宽的2倍,M是BC的中点,则∠AFE的度数为 15° .
15.如图所示,在矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 (1+2,2) .
16.如图所示,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF,GH之间任意一点,连结PE,PF,PG,PH,则△PEF和△PGH的面积和等于 7 .
17.如图所示,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:AE=DC.
(2)已知DC=,求BE的长.
(1)∵在矩形ABCD中,∠A=∠D=90°,∴∠1+∠2=90°.
∵EF⊥EC,∴∠FEC=90°.∴∠2+∠3=90°.∴∠1=∠3.
在△AEF和△DCE中,∵
∴△AEF≌△DCE(AAS).∴AE=DC.
(2)由(1)得AE=DC,∴AE=DC=,
在矩形ABCD中,AB=CD=,
在Rt△ABE中,,即.
18.如图所示,点E是矩形ABCD的边BC的延长线上一点,连结AE交CD于点F,G是AF的中点,再连结DG,DE,且DE=DG.
(1)求证:∠DEA=2∠AEB.
(2)若BC=2AB,求∠AED的度数.
(1)∵四边形ABCD是矩形,∴∠ADF=90°,AD∥BC.
∵Rt△ADF中,G是AF中点,∴GA=GD=GF.∴∠DGF=2∠DAE.
∵AD∥BE,∴∠AEB=∠DAE.
∵DG=DE,∴∠DEA=∠DGF.∴∠DEA=2∠AEB.
(2)过点G作GH⊥DC于H.
∵AD∥GH,G是AF中点,∴GH=AD=AB=DC.
∵DE=DG=GF,∴Rt△GHF≌Rt△DCE(HL).
∵∠DEA=2∠AEB,∴∠DCE=∠GFH=3∠AEB=3∠DAE.
∵∠DAE+∠GFH=90°,∴4∠DAE=90°,∠DAE=22.5°.∴∠DEA=2∠DAE=45°.
【中考实战演练】
19.【鄂尔多斯】如图所示,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( D )
A.
14
B.
16
C.
17
D.
18
20.【攀枝花】如图所示,在平面直角坐标系中,O为坐标原点,在矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为 (2.5,4),(3,4),(2,4),(8,4) .
【开放应用探究】
21.如图所示,点E为矩形ABCD外一点,DE⊥BD于点D,DE=CE,BD的垂直平分线交AD于点F,交BD于点G.连结EF交BD于点H.
(1)若∠CDE=∠DEH=∠HEC,求∠ABG的度数.
(2)求证:H是EF的中点.
(1)设∠CDE=x°.
∵DE=CE,∴∠CDE=∠DCE=x°.
∵∠CDE=∠DEH=∠HEC,
∴∠DEH=x°,∠HEC=2x°.
∵∠CDE+∠DEC+∠DCE=180°,
∴5x=180,解得x=36.
∵DE⊥BD,∴∠EDB=90°.∴∠BDC=90°﹣36°=54°.
∵四边形ABCD是矩形,
∴AB∥CD.∴∠ABG=∠BDC=54°.
(2)如图所示,连结AC,GE,CD与GE交于点M.
∵四边形ABCD是矩形,
∴AC=BD,AG=GC,BG=GD.∴GD=GC.
∴点G在CD的垂直平分线上.∵DE=CE,
∴点E在CD的垂直平分线上.
∴GE为CD的垂直平分线.∴DM=CM.
∵BG=DG,∴GM∥BC.
∵□ABCD是矩形,∴AD∥BC.
∴FD∥GE.
∵FG⊥BD,DE⊥BD,∴FG∥DE.
∴四边形FDEG是平行四边形.∴H为EF的中点.
5.1 矩形(2)
重点提示:判定一个四边形是矩形有三种方法:(1)有一个角是直角的平行四边形是矩形.(2)有三个角是直角的四边形是矩形.(3)对角线相等的平行四边形是矩形.注意方法(1)和(3)要先利用平行四边形的判定方法证明四边形是平行四边形.
【夯实基础巩固】
1.在□ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出□ABCD是矩形,那么这个条件可以是( B )
A.
AB=BC
B.
AC=BD
C.
AC⊥BD
D.
AB⊥BD
2.下列说法中正确的是( C )
A.
两组对角分别相等的四边形是矩形
B.
两个角是直角的四边形是矩形
C.
一个角是直角的平行四边形是矩形
D.
一个角是直角,一组对边相等的四边形是矩形
3.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( D )
A.
测量对角线是否相互平分
B.
测量两组对边是否分别相等
C.
测量对角线是否相等
D.
测量其中三个角是否都为直角
4.如图所示,四边形ABCD的对角线AC,BD相交于点O,给出下列条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( C )
A.
①②③
B.
②③④
C.
②⑤⑥
D.
④⑤⑥
5.已知四边形ABCD的两条对角线AC,BD互相垂直,E,F,G,H分别是四边形ABCD各边的中点.若AC=6,BD=8,则四边形EFGH的面积为( C )
A.48 B.24 C.12 D.条件不足,无法计算
6.如图所示,在□ABCD中,对角线AC,BD相交于点O,且OA=OB,∠OAD=65°.则∠ODC= 25° .
7.如图所示,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连结AE,BF.当∠ACB= 60° 时,四边形ABFE为矩形.
8.在平面直角坐标系中,有A(﹣2,﹣2),B(2,2),C(0,4)三个点,当点D的坐标为 (﹣4,0) 时,四边形ABCD是矩形.
9.如图所示,在□中,对角线AC与BD交于点O,OM⊥BC于点M,且BM=CM.
求证:□是矩形.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
又∵OM⊥BC,BM=CM,∴OB=OC.
∴AC=BD.∴□ABCD是矩形.
10.如图所示,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:
(1)△ABE≌△ACD.
(2)四边形BCDE是矩形.
(1)∵∠BAD=∠CAE,∴∠EAB=∠DAC.
在△ABE和△ACD中,∵∴△ABE≌△ACD(SAS).
(2)∵△ABE≌△ACD,∴BE=CD,
∵DE=BC,∴四边形BCDE为平行四边形.
∵AB=AC,∴∠ABC=∠ACB.
∵△ABE≌△ACD,∴∠ABE=∠ACD.∴∠EBC=∠DCB.
∵四边形BCDE为平行四边形,∴EB∥DC.
∴∠EBC+∠DCB=180°.∴∠EBC=∠DCB=90°.
∴四边形BCDE是矩形.
【能力提升培优】
11.平行四边形内角平分线能够围成的四边形是( B )
A.
梯形
B.
矩形
C.
正方形
D.
不是平行四边形
12.如图所示,在△ABC中,AC的中垂线交AC,AB于点D,F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( A )
A.
2
B.
2
C.
3
D.
3
13.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连结EF,则线段EF的最小值是( B )
A.
2.5
B.
2.4
C.
2.2
D.
2
14.如图所示,将□ABCD的边DC延长到点E,使CE=CD,连结AE交BC于点F,∠AFC=n∠D,当n= 2 时,四边形ABEC是矩形.
15.如图所示,已知□ABCD,给出下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC.其中能说明□ABCD是矩形的有(填写序号) ①④ .
16.如图所示,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF中点,则AM的取值范围是 ≤AM<6 .
17.如图所示,在△ABC中,O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
(1)∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6.∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.∴OE=OF.
(2)如图所示,∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,∴EF==13.
∴OC=EF=.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO.
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴□AECF是矩形.
18.如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA的延长线于点E,PF⊥AC交AC的延长线于点F.
(1)求证:四边形AEPF是矩形.
(2)D为BC中点,连结DE,DF.求证:DE=DF.
(1)∵∠BAC=90°,PE⊥AB,PF⊥AC.
∴四边形AEPF是矩形.
(2)连结DA.∵∠BAC=90°,AB=AC,D为BC中点,
∴DA=DC,∠DAE=∠DCF=135°.
又由(1)知AE=PF,△CFP是等腰直角三角形,
∴CF=PF=AE.∴△DAE≌△DCF.∴DE=DF.
【中考实战演练】
19.【临沂】如图所示,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( B )
A.
AB=BE
B.
DE⊥DC
C.
∠ADB=90°
D.
CE⊥DE
20.【内江】如图所示,将□ABCD的边AB延长至点E,使AB=BE,连结DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC.
(2)连结BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
(1)在□ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,∴BE=DC.
∴四边形BECD为平行四边形.∴BD=EC.
在△ABD与△BEC中,∵∴△ABD≌△BEC.
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC.∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.∴□BECD为矩形.
【开放应用探究】
21.已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,易证得结论PA2+PC2=PB2+PD2,请你探究:当点P分别在图2、图3中的位置时,PA2,PB2,PC2和PD2又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图2证明你的结论.
对图2的探究结论为 ;对图3的探究结论为 ;
结论均是PA2+PC2=PB2+PD2.
证明:如图所示,过点P作MN∥AB,交AD于点M,交BC于点N.
∴四边形ABNM和四边形NCDM均为矩形,
根据(1)中的结论可得,在矩形ABNM中有PA2+PN2=PB2+PM2,在矩形NCDM中有PC2+PM2=PD2+PN2,
两式相加得PA2+PN2+PC2+PM2=PB2+PM2+PD2+PN2,
∴PA2+PC2=PB2+PD2.
5.2 菱形(1)
重点提示:(1)菱形的定义:有一组邻边相等的平行四边形是菱形.(2)菱形的性质:菱形是特殊的平行四边形,它具有平行四边形的所有性质,菱形的四条边都相等,菱形的对角线互相垂直且每条对角线平分一组对角.(3)菱形既是中心对称图形又是轴对称图形,对角线所在直线是它的对称轴.
【夯实基础巩固】
1.菱形具有而平行四边形不具有的性质是( D )
A.
两组对边分别平行
B.
两组对角分别相等
C.
对角线互相平分
D.
对角线互相垂直
2.如图所示,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( D )
A.
10
B.
C.
6
D.
5
3.如图所示,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( B )
A.
18
B.
18
C.
36
D.
36
4.如图所示,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E,F,连结EF,则△AEF的面积是( B )
A.
4
B.
3
C.
2
D.
5.一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( C )
A.
3:1
B.
4:1
C.
5:1
D.
6:1
6.如图所示,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 (4,4) .
7.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 .
8.如图所示,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于点H,连结OH,则∠DHO= 25° .
9.如图所示,在菱形ABCD中,AE⊥BC,点E为垂足,且BE=CE,AB=2.求:
(1)∠BAD的度数.
(2)对角线AC的长及菱形ABCD的周长.
(1)∵在菱形ABCD中,AE⊥BC,且BE=CE,∴△ABC为等边三角形 ,∠ B=∠D=60°.
∴∠BAD=∠BCD=120°.
(2)AC=AB=2,菱形ABCD的周长为4×2=8.
10.如图所示,菱形ABCD的对角线AC,BD相交于点O,E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论.
(2)若AB=13,AC=10,求线段EF的长.
(1)△OEF是等腰三角形.
证明:∵四边形ABCD是菱形,
∴AB=AD,OA=OC,OB=OD.
∵点E,F分别是边AB,AD的中点,
∴EO=AB,OF=AD.
∴EO=FO,∴△OEF是等腰三角形.
(2)∵四边形ABCD是菱形,AC=10,
∴AO=5,∠AOB=90°,∴BO==12.∴BD=24.
∵点E,F分别是边AB,AD的中点,
∴EF=BD=12.
【能力提升培优】
11.如图所示,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于( A )
A. B. C.12 D.24
12.如图所示,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC等于( C )
A.
35°
B.
45°
C.
50°
D.
55°
13.如图所示,3个全等的菱形按如图所示方式拼合在一起,恰好得到一个边长相等的六边形,则菱形较长的对角线与较短的对角线之比是( A )
A.
B.
C.
2
D.
14.如图所示,在菱形ABCD中,点E是AB上的一点,连结DE交AC于点O,连结BO,且∠AED=50°,则∠CBO= 50° .
15.如图所示,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作点P到直线AB,AD的垂线段PE,PF,则PE+PF= 3 .
16.如图所示,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8﹣8,则菱形ABCD的边长为 2 .
17.如图所示,在菱形ABCD中,对角线AC,BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为矩形.
(2)在BC上截取CF=CO,连结OF,若AC=8,BD=6,求四边形OFCD的面积.
(1)∵DE∥AC,CE∥BD,∴四边形OCED为平行四边形.
∵四边形ABCD是菱形,∴AC⊥BD.∴∠DOC=90°.
∴四边形OCED为矩形.
(2)∵四边形ABCD是菱形,∴AC与BD互相垂直平分于点O.
∴OD=OB=BD=3,OA=OC=AC=4.
∴S△DOC=6.
在Rt△OBC中,BC==5,CF=OC=4.
∴S△OCF=.∴S四边形OFCD=S△DOC+S△OCF=6+=.
18.如图所示,在菱形ABCD中,∠B=60°,点E,F分别在边BC,CD上.
(1)若AB=4,试求菱形ABCD的面积.
(2)若∠AEF=60°,求证:AB=CE+CF.
(1)在菱形ABCD中,AB=BC,
∵∠B=60°,∴△ABC是等边三角形.
∵AB=4,∴等边三角形ABC底边BC上的高为4×=2.
∴菱形ABCD的面积=4×2=8.
(2)如图所示,将△AEC绕点A顺时针旋转60°得到△AE′B,则△AEE′为等边三角形,∴∠AE′E=60°.
∵∠AEF=60°,∴∠CEF=∠AEC﹣∠AEF=∠AEC﹣60°.
又∵∠BE′E=∠AE′B﹣∠AE′E=∠AE′B﹣60°,∴∠BE′E=∠CEF.
∵∠B=60°,菱形的对边AB∥CD,∴∠ECF=180°﹣60°=120°.
又∵∠E′BE=∠ABC+∠ABE′=∠ABC+∠ACB=60°+60°=120°,
∴∠E′BE=∠ECF.∴△EE′B≌△FEC(ASA).∴BE=CF.
∴BC=CE+BE=CE+CF.∵AB=BC,∴AB=CE+CF.
【中考实战演练】
19.【本溪】如图所示,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
20.【安徽】如图所示,在矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A.
2
B.
3
C.
5
D.
6
【开放应用探究】
21.有一种汽车用“千斤顶”,它由4根连杆组成菱形ABCD,当螺旋装置顺时针旋转时,B,D两点的距离变小,从而顶起汽车.若AB=30,螺旋装置每顺时针旋转1圈,BD的长就减少1.设BD=a,AC=h.
(1)当a=40时,求h值.
(2)从a=40开始,设螺旋装置顺时针旋转x圈,求h关于x的函数表达式.
(3)从a=40开始,螺旋装置顺时针连续旋转2圈,设第1圈使“千斤顶”增高s1,第2圈使“千斤顶”增高s2,试判定s1与s2的大小,并说明理由.若将条件“从a=40开始”改为“从某一时刻开始”,则结果如何,为什么?
(1)连结AC交BD于点O.
∵四边形ABCD为菱形,a=40,∴∠AOB=90°,OA=,OB=20.
在Rt△AOB中,
∵AO+BO=AB,即,∴h=20.
(2)从a=40开始,螺旋装置顺时针旋转x圈,则BD=40﹣x,
∴.∴h=.
(3)s1>s2.理由如下:
在h=中,
令x=0得,h0=≈44.721;
令x=1得,h1=≈45.596;
令x=2得,h2=≈46.433;
∴s1=h1﹣h0≈0.88,s2=h2﹣h1≈0.84.∴s1>s2.
若将条件“从a=40开始”改为“从任意时刻开始”,则结论s1>s2仍成立.
∵,
而2a﹣1>2a﹣3,,
∴s1>s2.
5.2 菱形(2)
重点提示:判定一个四边形是菱形有三种方法:(1)一组邻边相等的平行四边形是菱形.(2)四条边相等的四边形是菱形.(3)对角线互相垂直的平行四边形是菱形.注意方法(1)和(3)要先利用平行四边形的判定方法证明四边形是平行四边形.
【夯实基础巩固】
1.如图所示,要使□ABCD成为菱形,则需添加的一个条件是( B )
A.
AC=AD
B.
BA=BC
C.
∠ABC=90°
D.
AC=BD
2.如图所示,小明在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据他的作图方法可知,四边形ADBC一定是( B )
A.
矩形
B.
菱形
C.
正方形
D.
梯形
3.如图所示,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是( A )
A.
AB=BC
B.
AC=BC
C.
∠B=60°
D.
∠ACB=60°
4.下列说法中正确的是( A )
A.
四边相等的四边形是菱形
B.
一组对边相等,另一组对边平行的四边形是菱形
C.
对角线互相垂直的四边形是菱形
D.
对角线互相平分的四边形是菱形
5.如图所示是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
对于甲、乙两人的作法,可判断( C )
A.
甲正确,乙错误
B.
甲错误,乙正确
C.
甲、乙均正确
D.
甲、乙均错误
6.如图所示,在□ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,请添加一个条件: AE=EC(答案不唯一) ,使四边形AECF为菱形.
7.如图所示,矩形ABCD的对角线AC,BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长为 16 .
8.如图所示,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,且AD交EF于点O,则∠AOF= 90° .
9.如图所示,CE是△ABC的外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
∵AF∥CD,FG∥AC,
∴四边形ACGF是平行四边形,∠FCG=∠AFC.
∵CE平分∠ACD,∴∠ACF=∠GCF.∴∠ACF=∠AFC.
∴AC=AF.∴四边形ACGF是菱形.
10.如图所示,在△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连结BD,CE交于点F.求证:
(1)△ABD≌△ACE.
(2)四边形ABFE是菱形.
(1)由旋转可知∠DAE =∠BAC =40°,∴∠BAD=∠CAE=100°.
∵AB=AC,∴AB=AC=AD=AE.
∴△ABD≌△ACE(SAS).
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°.
∴∠BAE=∠BFE.∴四边形ABFE是平行四边形.
∵AB=AE,∴□ABFE是菱形.
【能力提升培优】
11.如图所示,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,这个条件可以是( D )
A.
AB//CD
B.
AC⊥BD
C.
AC=BD
D.
AD=BC
12.如图所示,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以cm/s的速度向终点A运动;同时,动点Q从点C出发沿CB方向以1cm/s的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t(s),若四边形QPBP′为菱形,则t的值为( B )
A.
B.
2
C.
2
D.
4
13.如图所示,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF交AC于点M,连结DE,BO.若∠COB=60°,FO=FC,给出下列结论:
①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2.
其中正确结论的个数有( C )
A.
1个
B.
2个
C.
3个
D.
4个
14.如图所示,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD,CB为边作□CDEB,当AD= ,□CDEB为菱形.
15.如图所示,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连结BG,DF.若FG=5,CF=6,则四边形BDFG的面积为 15 .
16.如图所示,在四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连结四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBnCnDn.下列结论中正确的有 ②③④ .
①四边形A2B2C2D2是矩形; ②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长为; ④四边形AnBnCnDn的面积是.
17.如图1所示,在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠DCE=90°,AB与CE交于点F,ED与AB,BC,分别交于点M,H.
(1)求证:CF=CH.
(2)如图2所示,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形,并证明你的结论.
(1)∵AC=CE=CB=CD,∠ACB=∠ECD=90°,
∴∠A=∠B=∠D=∠E=45°.
在△BCF和△ECH中,∵
∴△BCF≌△ECH(ASA).∴CF=CH.
(2)四边形ACDM是菱形.
证明:∵∠ACB=∠DCE=90°,∠BCE=45°,∴∠ACE=∠BCD=45°.
∵∠E=45°,∴∠ACE=∠E.
∴AC∥DE.∴∠AMH=180°﹣∠A=135°=∠ACD.
又∵∠A=∠D=45°,
∴四边形ACDM是平行四边形.
∵AC=CD,∴四边形ACDM是菱形.
18.如图所示,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连结DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
(3)在(2)的条件下,试确定点E的位置,使得∠EFD=∠BCD,并说明理由.
(1)在△ABC和△ADC中,∵
∴△ABC≌△ADC(SSS).∴∠BAC=∠DAC.
在△ABF和△ADF中,∵
∴△ABF≌△ADF(SAS).∴∠AFD=∠AFB.
∵∠AFB=∠CFE,∴∠AFD=∠CFE.
(2)∵AB∥CD,∴∠BAC=∠ACD.
∵∠BAC=∠DAC,∴∠CAD=∠ACD.∴AD=CD.
∵AB=AD,CB=CD,∴AB=CB=CD=AD.
∴四边形ABCD是菱形.
(3)当EB⊥CD时,∠EFD=∠BCD.理由如下:
∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF.
在△BCF和△DCF中,∵
∴△BCF≌△DCF(SAS).∴∠CBF=∠CDF.
∵BE⊥CD,∴∠BEC=∠DEF=90°.
∴∠BCD+∠CBE=∠CDF+∠EFD.∴∠EFD=∠BCD.
【中考实战演练】
19.【曲靖】如图所示,在矩形ABCD中,E,F分别是AD,BC中点,连结AF,BE,CE,DF分别交于点M,N,四边形EMFN是( B )
A.
正方形
B.
菱形
C.
矩形
D.
无法确定
20.【荆门】如图所示,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.
∵AB∥CD,∴∠DCA=∠BAC.
∵DF∥BE,∴∠DFA=∠BEC.∴∠AEB=∠CFD.
在△AEB和△CFD中,∵
∴△AEB≌△CFD(ASA).∴AB=CD.
∵AB∥CD,∴四边形ABCD是平行四边形.
∵AC平分∠BAD,∴∠BAE=∠DAF.
∵∠BAE=∠DCF,∴∠DAF=∠DCF.
∴AD=CD.∴四边形ABCD是菱形.
【开放应用探究】
21.如图1所示,P是线段AB上一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连结CD,点E,F,G,H分别是AC,AB,BD,CD的中点,顺次连结E,F,G,H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由.
(2)当点P在线段AB的上方时,如图2所示,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由.
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,不必说明理由.
(1)四边形EFGH是菱形. (2)成立.理由如下:
如图1所示,连结AD,BC. ∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB.
又∵PA=PC,PD=PB,∴△APD≌△CPB.∴AD=CB.
∵E,F,G,H分别是AC,AB,BD,CD的中点,
∴EF,FG,GH,EH分别是△ABC,△ABD,△BCD,△ACD的中位线.
∴EF=BC,FG=AD,GH=BC,EH=AD.
∴EF=FG=GH=EH.∴四边形EFGH是菱形.
(3)如图2所示,四边形EFGH是正方形.
5.3 正方形(1)
重点提示:判定一个四边形是正方形的方法一般有两种:一是先判定这个四边形是矩形,再说明它的邻边相等或对角线互相垂直;二是先判定这个四边形是菱形,再说明它有一个角是直角或对角线相等.
【夯实基础巩固】
1.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( C )
A.
平行四边形
B.
菱形
C.
正方形
D.
矩形
2.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是( D )
A.
AO=CO
B.
AO=CO=BO=DO
C.
AO=CO,BO=DO,AC⊥BD
D.
AO=BO=CO=DO,AC⊥BD
3.如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( D )个正方形.
A.
0
B.
1
C.
2
D.
3
4.甲、乙、丙、丁四位同学到工厂实习,工人师傅拿一把尺子要他们帮助检测一个四边形构件是否为正方形,他们各自做了如下检测:
甲量得构件四边都相等;
乙量得构件的两条对角线相等;
丙量得构件的一组邻边相等;
丁量得构件的四边相等且两条对角线也相等.
检测后,他们都说是正方形,你认为说得最有把握的是( D )
A.
甲
B.
乙
C.
丙
D.
丁
5.如图所示,将长方形纸片折叠,使点A落BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( A )
A.
邻边相等的矩形是正方形
B.
对角线相等的菱形是正方形
C.
两个全等的直角三角形构成正方形
D.
轴对称图形是正方形
6.如果一个四边形既是菱形又是矩形,那么它一定是 正方形 .
7.如图所示,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB:AD= 1:2 时,四边形MENF是正方形.
8.如图所示,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件 ∠ABC=90° 时,四边形BEDF是正方形.
9.如图所示,在矩形ABCD中,∠ABC的平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别为点E,F.判定四边形EBFM的形状,并证明你的结论.
四边形EBFM是正方形.
证明:∵四边形ABCD为矩形,∴∠ABC=90°.
∵MF⊥BC,ME⊥AB,∴∠BFM=∠MEB=90°.
∵∠ABC=∠BFM=∠MEB=90°,∴四边形EBFM为矩形.
∵BM平分∠ABC,∴ME=MF.∴四边形EBFM为正方形.
10.如图所示,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)求证:DE=DF.
(2)只添加一个条件,使四边形EDFA是正方形,请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明)
(1)∵AB=AC,∴∠B=∠C.∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.又∵D是BC的中点,∴BD=CD.∴△DEB≌△DFC.故DE=DF.
(2)略
【能力提升培优】
11.如图所示,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕所成角的度数为( C )
A.
22.5°
B.
30°
C.
45°
D.
60°
12.如图所示,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( B )
A.
30
B.
34
C.
36
D.
40
13.如图所示,在一张3×3的方格纸上,若以格点(即小正方形的顶点)为顶点画正方形,则在该3×3方格纸上最多可画出的正方形的个数是( D )
A.
13
B.
14
C.
18
D.
20
14.如图所示,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,则∠ACB= 90 度时,四边形AECF是正方形.
15.如图所示,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是 3 .
16.菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形就越接近正方形.
①当菱形的一个内角为70°时,“接近度”= .
②当菱形的“接近度”= 时,菱形就是正方形.
(2)若我们将菱形的“接近度”定义为(m<n),则:
①当菱形的一个内角为60°时,“接近度”= .
②当菱形的“接近度”= 时,菱形就是正方形.
(3)甲、乙两位同学仿照菱形的“接近度”的定义,给出了如下两种矩形的“接近度”的定义,在你认为合理的定义后面打“√”,不合理的打“×”.
①甲:设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a-b|,于是|a-b|越小,矩形越接近于正方形. ( ) ②乙:设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为,于是越小,矩形越接近于正方形. ( )
16.(1)①40 ②0 (2)① ②1 (3)①× ②√
17.如图所示,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连结CF.
(1)求证:D是BC的中点.
(2)如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论.
(3)当△ABC满足什么条件时,四边形ADCF为正方形?并证明你的结论.
(1)∵AF=DC,AF∥BC,∴四边形ADCF为平行四边形.∴AF=CD.
∵E为AD的中点,AF∥BD,∴AE=DE,∠AFE=∠DBE.
在△AEF和△DEB中,∵∴△AEF≌△DEB(AAS).
∴BD=AF.∴BD=CD,即D为BC的中点.
(2)四边形ADCF为矩形.理由如下:
连结AB.∵AB=AC,D为BC的中点,
∴AD⊥BC.∴∠ADC=90°.∴□ADCF为矩形.
(3)当△ABC为等腰直角三角形时,四边形ADCF为正方形.理由如下:
∵△ABC为等腰直角三角形,D为BC中点,
∴AD⊥BC,AD=BC=BD=CD.
∴矩形ADCF为正方形.
18.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图1所示),CE=2cm,将长方形ABCD绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.
(1)当旋转到顶点D,H重合时,连结AG(如图2所示),求点D到AG的距离.
(2)当α=45°时(如图3所示),求证:四边形MHND为正方形.
(1)作DK⊥AG于点K.
∵CD=CE=DE=2cm,∴△CDE是等边三角形.
∴∠CDE=60°.∴∠ADG=360°﹣2×90°﹣60°=120°.
∵AD=DG=1cm,∴∠DAG=∠DGA=30°.∴DK=DG=cm,
∴点D到AG的距离为cm.
(2)∵α=45°,∴∠NCE=∠NEC=45°.∴CN=NE.
∴∠CNE=90°.∴∠DNH=90°.
∵∠D=∠H=90°,∴四边形MHND是矩形.
∵CN=NE,∴DN=NH.∴矩形MHND是正方形.
【中考实战演练】
19.【日照】小明在学习了正方形之后,给同桌小文出了道题:下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD,请你从中选两个作为补充条件,使□ABCD为正方形(如图所示).现有下列四种选法,你认为其中错误的是( B )
A.
①②
B.
②③
C.
①③
D.
②④
20.如图所示,AB垂直平分CD,并交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为点E,F.
(1)求证:∠CAB=∠DAB.
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
(1)∵AB是CD的垂直平分线,∴AC=AD.
∵AB⊥CD,∴∠CAB=∠DAB.
(2)∵ME⊥A C,MF⊥AD,∠CAD=90°,即∠CAD=∠AEM=∠AFM=90°,
∴四边形AEMF是矩形.
又∵∠CAB=∠DAB,ME⊥A C,MF⊥AD,
∴ME=MF.∴矩形AEMF是正方形.
【开放应用探究】
21.以四边形ABCD的边AB,BC,CD,DA为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连结这四个点,得四边形EFGH.
(1)如图1所示,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2所示,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图3所示,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE.
②求证:HE=HG.
③四边形EFGH是什么四边形?请说明理由.
(1)四边形EFGH的形状是正方形.
(2)①∵在□ABCD中,AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣α.
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°.
∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣(180°﹣α)=90°+α.
②∵△AEB和△DGC是等腰直角三角形,
∴AE=AB,DG=CD.
∵在□ABCD中,AB=CD,∴AE=DG.
∵△AHD和△DGC是等腰直角三角形,∴∠HDA=∠CDG=45°.
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE.
∵△AHD是等腰直角三角形,∴HA=HD.
∴△HAE≌△HDG.∴HE=HG.
③四边形EFGH是正方形,理由如下:
由②同理可得GH=GF,FG=FE.
∵HE=HG,∴GH=GF=EF=HE.
∴四边形EFGH是菱形.
∵△HAE≌△HDG,∴∠DHG=∠AHE.
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°.
∴四边形EFGH是正方形.
5.3 正方形(2)
重点提示:正方形是最特殊的四边形,它综合了平行四边形、矩形和菱形的所有性质,正方形的四条都相等,四个角都是直角,对角线互相垂直平分并且相等,其对角线可以将正方形分成大小不同的八个等腰直角三角形.
【夯实基础巩固】
1.正方形具有而菱形不一定具有的性质是( D )
A.
四条边相等
B.
对角线互相垂直平分
C.
对角线平分一组对角
D.
对角线相等
2.若正方形的周长为40,则其对角线长为( C )
A.
100
B.
C.
D.
10
3.如图所示,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( D )
A.
45°
B.
55°
C.
60°
D.
75°
4.如图所示,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为( C )
A.
20°
B.
25°
C.
35°
D.
40°
5.如图所示,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( B )
A.n B.n﹣1 C. D.n
6.如图所示,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 5 .
7.如图所示,在正方形ABCD外侧,作等边三角形ADE,连结AC,BE相交于点F,则∠BFC= 60 度.
8.如图所示,边长为8的正方形ABCD中,M是BC上的一点,连结AM,作AM的垂直平分线GH交AB于点G,交CD于点H,若CM=2,则GH= 10 .
9.如图所示,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连结BE,DF,DF交对角线AC于点P,且DE=DP.求证:
(1)AE=CP.
(2)BE∥DF.
(1)∵DE=DP,∴∠DEP=∠DPE.
∴∠AED=∠CPD.
∵四边形ABCD是正方形,
∴AD=CD=BC,∠DAC=∠BCE=∠DCA=45°.
∴△ADE≌△CDP(AAS).∴AE=CP.
(2)在△BCE和△DCE中,∵
∴△BCE≌△DCE (SAS).∴∠BEC=∠DEP.
∴∠BEC=∠DPE.∴BE∥DF.
10.如图所示,在正方形ABCD中,点E在BC的延长线上,AE分别交DC,BD于点F,G, H为EF的中点.求证:
(1)∠DAG=∠DCG.
(2)GC⊥CH.
(1)∵四边形ABCD为正方形,∴AD=DC,∠ADB=∠CDB=45°.
∵DG=DG,∴△ADG≌△CDG.∴∠DAG=∠DCG.
(2)∵四边形ABCD为正方形,∴AD∥BE,
∴∠DAG=∠E.∵∠DAG=∠DCG,∴∠E=∠DCG.
∵H为Rt△CEF斜边EF边的中点,∴CH=HE=EF.
∴∠HCE=∠E,∴∠DCG=∠HCE.
∵∠FCH+∠HCE=90°,
∴∠FCH+∠DCG=90°,即∠GCH=90°.∴GC⊥CH.
【能力提升培优】
11.如图所示,在正方形ABCD中,对角线AC,BD相交于O,AB=2,E是BC中点,点P在对角线AC上滑动,则BP+EP的最小值是( C )
A.
B.
2
C.
D.
3
12.如图所示,在正方形ABCD中,E,F分别是边CD,AD上的点,且CE=DF,AE与BF相交于点O,则下列结论中错误的是( C )
A.
AE=BF
B.
AE⊥BF
C.
AO=OE
D.
S△AOB=S四边形DEOF
13.如图所示,在正方形ABCD中,AD=5,E,F是正方形ABCD内两点,且AE=CF=3,BE=DF=4,则EF的长为( D )
A. B. C. D.
14.如图所示,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点,已知四边形ABCD是正方形,则k的值为 .
15.如图所示,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
16.如图所示,四边形ABCD是正方形,E是CF上一点,若四边形DBEF是菱形,则∠EBC= 15° .
【解析】过点D作DG⊥CF于点G.设正方形ABCD的边长为1,则由勾股定理可得BD=.
∵四边形ABCD为正方形,四边形DBEF为菱形,∴DF=BD=,∠DCG=∠CDB=45°.
∵DG⊥CF,∴△CDG为等腰直角三角形.∴DG=.∴在Rt△DFG中,DF=2DG.∴∠F=30°.∴∠DBE=∠F=30°.∴∠EBC=45°-30°=15°.
17.如图所示,G是正方形ABCD的对角线CA延长线上的任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD.
(2)若AB=3,AG=3,求EB的长.
(1)∵四边形ABCD,AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG.
∴∠EAB=∠GAD.∴△EAB≌△GAD(SAS).
(2)∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD=AB=6.
∴∠DOG=90°,OA=OD=BD=3.
∵AG=3,∴OG=OA+AG=6.
∴GD=.∴EB=.
18.如图1所示,在正方形ABCD中,E为BC上一点,过点B作BG⊥AE于点G,延长BG至点F,使∠CFB=45°.
(1)求证:AG=FG.
(2)如图2所示,延长FC,AE交于点M,连结DF,BM,若C为FM中点,BM=10,求FD的长.
(1)如图1所示,过点C作CH⊥BF于点H.
∵∠CFB=45°,∴CH=HF.
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,∴∠BAG=∠FBE.
∵AG⊥BF,CH⊥BF,∴∠AGB=∠BHC=90°.
又∵四边形ABCD为正方形,∴AB=BC.
∴△AGB≌△BHC.∴AG=BH,BG=CH.
∵BH=BG+GH,∴BH=CH+GH=HF+GH=FG.∴AG=FG.
(2)如图2所示,过点C作CH⊥BF于点H,过点B作BK⊥CM于K,过点D作DQ⊥MF交MF延长线于Q.
∵CH⊥GF,∴CH∥GM.
∵C为FM的中点,∴CH=GM.∴BG=GM.
∵BM=10,∴BG=2,GM=4.
∴AG=4,AB=10.∴HF=2.∴CF=2×=2.∴CM=2.
∵CK=CM=CF=,∴BK=3.∴△BKC≌△CQD.
∴CQ=BK=3,DQ=CK=.
∴QF=3﹣2=,∴DF==2.
【中考实战演练】
19.如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连结EF.给出下列结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,其中正确的结论个数有( B ).
A.
5个
B.
4个
C.
3个
D.
2个
20.【黄冈】如图所示,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED= 65 度.
【开放应用探究】
21.如图所示,在正方形ABCD中,AC,BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
(1)若点E在图1的位置,判断OE与OF的数量关系,并证明你的结论.
(2)若点E在AC的延长线上,请在图2中按题目要求补全图形,判断OE与OF的数量关系,并证明你的结论.
(1)OE=OF.理由如下:
∵在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°,
∴∠OBE+∠BEO=90°.
∵AH⊥EB,∴∠AHE=90°.
∴∠HAE+∠AEH=90°.∴∠OBE=∠OAF.
∴△AOF≌△BOE(ASA).∴OE=OF.
(2)OE=OF仍然成立.理由如下:
如图所示,∵在正方形ABCD中,AO=BO,∠AOF=∠BOE=90°,
∴∠FAO+∠F=90°.
∵AH⊥EB,∴∠AHE=90°.
∴∠HAE+∠E=90°.∴∠E=∠F.
∴△AOF≌△BOE(AAS).∴OE=OF.
∴结论仍然成立.
专题复习一 方程思想与几何计算
重点提示:方程思想是数学重要思想方法,在几何计算中,当直接计算有困难时,列方程解决问题是重要思路,常用于列方程的等量关系有三角形(多边形)的内角和定理、勾股定理等.
【夯实基础巩固】
菱形的周长为20cm,两邻角的比为1:3,则菱形的面积为( C )
A.25cm2 B.16cm2 C.cm2 D.cm2
2.已知菱形的周长为40,两条对角线之比3:4,则菱形面积为( D )
A.
12
B.
24
C.
48
D.
96
3.如图所示,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF为( A )
A.
6.5dm
B.
6dm
C.
5.5dm
D.
4dm
4.如图所示,在菱形ABCD中,E,F分别是边AB和BC的中点,EP⊥CD于点P,设∠A=x°,则∠FPC的度数为( D )
A.° B.° C.° D.°
5.如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( A )
A.
3cm
B.
4cm
C.
5cm
D.
6cm
6.如图所示,在矩形ABCD中,两个小正方形的面积分别为S1,S2.若S1=4,S2=16,则图中阴影部分面积为 4 .
7.如图所示,在矩形ABCD中,AB=7cm,BC=cm,点P从点A出发以1cm/s的速度移动到点B.点P出发 s后,PA=2PC.
8.如图所示,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 (10,3) .
9.如图所示,P是矩形ABCD内一点,若PA=3,PB=4,PC=5,则PD= 3 .
10.如图所示,等腰三角形CEF的两腰CE,CF的长与菱形ABCD的边长相等,点E,F分别在AB,AD上.
(1)求证:△BEC≌△DFC.
(2)当△ECF是等边三角形时,求∠B的度数.
(1)∵四边形ABCD是菱形.∴CB=CD,且∠B=∠D.
∵△CEF是等腰三角形,∴CE=CF.
∵CE=CB,CF=CD,∴∠B=∠CEB,∠D=∠CFD.
∴∠CEB=∠CFD.∴△BEC≌△DFC(AAS).
(2)设∠B=x.∵CE=CB,∴∠CEB=∠B=x.∴∠BCE=180﹣2x.
同理∠FCD=180﹣2x.
∵△CEF是等边三角形,∴∠ECF=60°.
∵四边形ABCD是菱形.∴∠B+∠BCD=180°.
∴x+2(180﹣2x)+60°=180°,解得x=80°.
∴∠B=80°.
【能力提升培优】
11.已知正方形ABCD的边长是10cm,△APQ是等边三角形,点P在BC上,点Q在CD上,则BP等于( C )
A.cm B.cm
C.cm D. cm
12.如图所示,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4,则FD的长为( B )
A.
2
B.
4
C.
D.
2
13.如图所示,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速运动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t s△DEF为等边三角形,则t的值为 .
14.正方形OA1B1C1,A1A2B2C2,A2A3B3C3按如图所示放置,其中点A1,A2,A3在x轴的正半轴上,点B1,B2,B3在直线y=﹣x+2上,则点A3的坐标为 .
15.如图所示,矩形ABCD被分成四部分,其中△ABE,△ECF,△ADF的面积分别为2,3,4,则△AEF的面积为 7 .
【解析】设AB=x,BC=y.∵,∴BE=.
∴EC=.∵,∴FC=.
∴DF=.∴.
化简得,即,解得xy=2(舍去)或xy=16.
∴.
16.如图所示,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/s的速度运动,点Q从点C开始沿CB边向点B以2cm/s的速度运动,如果点P,Q分别从点A,C同时出发,设运动时间为t(s).求:
(1)当t为何值时,四边形ABQP为矩形?
(2)当t为何值时,四边形PQCD为平行四边形?
(1)由题意知AP=t cm,CQ=2t cm,∴BQ=(21﹣2t)cm.
∵AD∥BC,∴AP∥BQ.
又∵∠B=90°,∴要使四边形ABQP为矩形,只需满足AP=BQ,即t=21﹣2t,解得t=7.
∴当t=7时,四边形ABQP为矩形.
(2)由题意知AP=t cm,QC=2t cm,PD=(18﹣t)cm,当PD=QC时,四边形PACD为平行四边形,
即18﹣t=2t,解得t=6.
∴当t=6时,四边形PQCD为平行四边形.
17.如图所示,在矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF,BF.
(1)若DG=2,求证:四边形EFGH为正方形.
(2)若AE=x,求△EBF的面积S关于x的函数表达式,并判断是否存在x,使△EBF的面积是△CGF面积的2倍?若存在,求出x的值;若不存在,请说明理由.
(1)∵四边形ABCD是矩形,∴∠D=∠A=90°.
∵四边形EFGH是菱形,∴HG=HE.
在Rt△HDG和Rt△AEH中,∵
∴Rt△HDG≌Rt△EAH(HL).
∴∠DHG=∠AEH.∴∠DHG+∠AHE=90°.
∴∠GHE=90°.∴菱形EFGH为正方形.
(2)如图所示,过点F作FM⊥AB交AB的延长线于点M,MF与DC的延长线交于点N,连结GE.
∴FN⊥CD.
∵CD∥AB,∴∠DGE=∠MEG.
∵GH∥EF,∴∠HGE=∠FEG.∴∠DGH=∠MEF.
∴Rt△HDG≌Rt△FME.
∴DH=MF.∴AH=2.∴DH=MF=4.
∵AE=x,∴BE=10﹣x.
∴S△EBF=BE?FM=2(10﹣x)=20﹣2x.
S关于x的函数表达式为S=20﹣2x.
同理可证Rt△AHE≌Rt△FNG,∴FN=AH=2.
∵AH=2,AE=x,∴HE=HG=.
∴DG=.
∴CG=10﹣.∴S△GCF=CG?FN=10﹣.
若△EBF的面积是△CGF面积2倍,则
20﹣2x=2(10﹣),整理得x2=x2﹣12,此方程无解,
∴不存在x,使△EBF的面积是△CGF面积的2倍.
【中考实战演练】
18.【安顺】如图所示,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( A )
A.
B.
C.
D.
6
19.【荆州】如图所示,在矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于点D,则点D的坐标为 (0,2.1) .
【开放应用探究】
20.如图所示,在正方形ABCD中,DE与HG相交于点O.
(1)如图1所示,若∠GOD=90°,①求证:DE=GH. ②连结EH,求证:GD+EH≥DE.
(2)如图2所示,若∠GOD=45°,AB=4,HG=2,求DE的长.
(1)①如图1所示,过点D作DM//GH交BC的延长线于点M,则四边形GDMH为平行四边形,∴GH=DM,GD=MH,GH∥DM,
∴∠GOD=∠MDE=90°.∴∠MDC+∠EDC=90°.
∵∠ADE+∠EDC=90°,∴∠MDC=∠ADE.
∴△ADE≌△CDM.∴DE=DM.∴DE=GH.
②连结EH,EM.∵DM=DE,∠EDM=90°,∴△EDM是等腰直角三角形.
∴EM=DM=GH=DE.
∵MH+EH≥EM,GD=MH,∴EH+GD≥EM.∴GD+EH≥DE.
(2)如图2所示,过点D作DN∥GH交BC于点N,则四边形GHND是平行四边形,
∴DN=HG,GD=HN.
∵∠C=90°,CD=AB=4,HG=DN=2,∴CN==2.
∴BN=BC﹣CN=4﹣2=2.
作∠ADM=∠CDN,DM交BA的延长线于点M,
∴△ADM≌△CDN.
∴AM=NC,∠ADM=∠CDN,DM=DN.
∵∠GOD=45°,∴∠EDN=45°.
∴∠ADE+∠CDN=45°.∴∠ADE+∠ADM=45°=∠MDE.
∴△MDE≌△NDE.
∴EM=EN,即AE+CN=EN.设AE=x,则BE=4﹣x,
在Rt△BEN中,由勾股定理得,解得x=.
∴DE=.
专题复习二 转化思想与特殊四边形问题
重点提示:在研究新问题或复杂问题时,常常把问题转化为已知的或比较简单的问题来解决,因此转化思想在几何证明和计算中是一个重要的数学思想.在解与特殊四边形有关的问题时,常常将问题转化为特殊三角形问题解决.
【夯实基础巩固】
1.如图所示,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE等于( C )
A.
20°
B.
25°
C.
30°
D.
35°
2.如图所示,矩形ABCD的周长为68,它被分成7个全等的矩形,则矩形ABCD的面积为( C )
A.
98
B.
196
C.
280
D.
284
3.如图所示,把矩形ABCD沿EF翻折,点B恰好落在AD边的点B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( D )
A.
12
B.
24
C.
12
D.
16
4.如图所示,P是正方形ABCD的边AB上一点(点P不与点A,B重合),连结PD并将线段PD绕点P顺时针旋转90°,得线段PE,连结BE,则∠CBE等于( C )
A.
75°
B.
60°
C.
45°
D.
30°
5.如图所示,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分的面积与四边形EMCN的面积之比为( C )
A.
4:3
B.
3:2
C.
14:9
D.
17:9
6.如图所示,矩形ABCD的面积是16,EF过矩形ABCD对角线的交点O,阴影部分的面积是 4 .
7.如图所示,正方形ABCD的周长为16cm,则矩形EFCH的周长是 8 cm.
8.如图所示,在菱形ABCD中,边AB的垂直平分线与对角线AC相交于点E,若∠ABC=140°,则∠EDC= 120° .
9.如图所示,在正方形ABCD中,点H在BC上,EF⊥AH交AB于点E,交AH于点G,交DC于点F.若AB=3,BH=1,求EF的长.
如图所示,作FM⊥AB于点M,则FM=AB=3.
∵∠1+∠3=∠2+∠3=90°,∴∠1=∠2.
又∵FM=AB,∴Rt△FME≌Rt△ABH.
∴.
10.在菱形ABCD中,O是对角线的交点,E是边CD的中点,点F在BC的延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形.
(2)连结DF,如果DF⊥CF,请你写出图中所有的等边三角形.
(1)∵四边形ABCD是菱形,∴BO=DO.
∵E是边CD的中点,∴OE是△BDC的中位线.
∴OEBC.
∵CF=BC,∴OE CF.
∴四边形OCFE是平行四边形.
(2)图中的等边三角形有:△OCE,△ECF,△ABC,△ADC.
【能力提升培优】
11.如图所示,E,F分别是矩形ABCD的边AD,BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为( C )
A.
15
B.
20
C.
35
D.
40
12.如图所示,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( B )
A. B. C. D.
13.在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连结AE,BE,FA⊥AE交DP于点F,连结BF,FC.给出下列结论:①△ABE≌△ADF;②FB=AB;③CF⊥DP;④FC=EF. 其中正确的结论有( D )
A.
①②④
B.
①③④
C.
①②③
D.
①②③④
14.已知正方形ABCD的边长为4,点E在直线CD上,CE=2,点P在边AC上,且PB⊥PE,则PC的长为 3 .
15.如图所示,正方形ABCD的AB边上有一点P,AD边上有一点Q,且PQ=BP+DQ,则∠QCP= 45° .
16.如图所示,P为正方形ABCD内一点,若PA:PB:PC=1:2:3,则∠APB= 135° .
17.如图所示,在菱形ABCD中,∠B=60°,点E,F分别在边BC,CD上.
(1)若AB=4,试求菱形ABCD的面积.
(2)若∠AEF=60°,求证:AB=CE+CF.
(1)∵在菱形ABCD中,∠B=60°,
∴△ABC是等边三角形.
∵AB=4,∴等边三角形ABC底边上的高为4×=2.
∴菱形ABCD的面积=4×2=8.
(2)如图所示,将△AEC绕点A顺时针旋转60°得到△AE′B,则△AEE′为等边三角形.∴∠AE′E=60°.
∵∠AEF=60°,∴∠CEF=∠AEC﹣∠AEF=∠AEC﹣60°.
∵∠BE′E=∠AE′B﹣∠AE′E=∠AE′B﹣60°,∴∠BE′E=∠CEF.
∵∠B=60°,∴∠ECF=180°﹣60°=120°.
∵∠E′BE=∠ABC+∠ABE′=∠ABC+∠ACB=60°+60°=120°,∴∠E′BE=∠ECF.
在△EE′B和△FEC中,∵∴△EE′B≌△FEC(ASA).
∴BE=CF.∴BC=CE+BE=CE+CF.
∵AB=BC,∴AB=CE+CF.
18.如图所示,AC是正方形ABCD的对角线,O是AC的中点,Q是AB上一点,连结CQ,DP⊥CQ于点E,交BC于点P,连结OP,OQ.求证:
(1)△BCQ≌△CDP.
(2)OP=OQ.
(1)∵四边形ABCD是正方形,∴∠QBC=∠PCD=90°,BC=CD. ∴∠2+∠3=90°.
又∵DP⊥CQ,∴∠2+∠1=90°.∴∠1=∠3. ∴△BCQ≌△CDP.
(2)如图所示,连结OB.
∵△BCQ≌△CDP,∴BQ=PC.
∵四边形ABCD是正方形,∴∠ABC=90°,AB=BC.
∵O是AC中点,∴BO=AC=CO,∠4=∠ABC=45°=∠PCO.
在△BOQ和△COP中,∵
∴△BOQ≌△COP.∴OQ=OP.
【中考实战演练】
19.如图所示,菱形ABCD和菱形ECGF的边长分别为3和4,若∠A=120°,则图中阴影部分的面积是 .
20.如图所示,在正方形ABCD外取一点E,连结AE,BE,DE.过点A作AE的垂线交DE于点P,连结BP.若AE=AP=1,PB=.给出下列结论:①△APD≌△AEB﹔②点B到直线AE的距离为﹔③EB⊥ED﹔④S△APD+S△APB=+.其中正确的结论有( A )
A.
①③④
B.
①②③
C.
②③④
D.
①②④
【开放应用探究】
21.(1)有这样一道习题:如图1所示,在□ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为 和 .
(2)如图2所示,点P为□ABCD内一点,过点P分别作AD,AB的平行线分别交□ABCD的四边于点E,F,G,H.已知S□BHPE=3,S□PFDG=5,则S△PAC= .
(3)如图3所示,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形的面积和为14,四边形ABCD的面积为11,求菱形EFGH的周长.
(1)□AEPH 和□PGCF 或□ABGH 和□EBCF 或□AEFD 和□HGCD.
(2)1
(3)∵①②③④四个平行四边形的面积和为14,
∴
∵四边形ABCD的面积为11,∴
∴
设菱形EFGH的边长为x.
∵菱形的一个内角为30°,∴菱形EFGH的高为.
∴,解得x=6.
∴菱形EFGH的周长为6×4=24.
第5章综合测评卷
一、选择题(每题3分,共30分)
1.正方形是轴对称图形,它的对称轴共有( D )
A.
1条
B.
2条
C.
3条
D.
4条
2.如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连结AE,CF,则四边形AECF是( C )
A.
梯形
B.
矩形
C.
菱形
D.
正方形
3.菱形的周长为16,且有一个内角为120°,则此菱形的面积为( B )
A.
4
B.
8
C.
10
D.
12
4.如图所示,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( C )
A.
14
B.
15
C.
16
D.
17
5.如图所示,已知四边形ABCD是菱形,过顶点D作DE⊥AD,交对角线AC于点E,若∠DAE=20°,则∠CDE的度数是( C )
A.
70°
B.
60°
C.
50°
D.
40°
6.用直尺和圆规作一个菱形,如图所示,能得到四边形ABCD是菱形的依据是( B )
A.
一组邻边相等的四边形是菱形
B.
四边相等的四边形是菱形
C.
对角线互相垂直的平行四边形是菱形
D.
每条对角线平分一组对角的平行四边形是菱形
7.如图所示,过矩形ABCD的对角线BD上任意一点O,分别作矩形两边的平行线EF和GH,图中矩形AHOE的面积记为S1,矩形CGOF的面积记为S2,则S1与S2的大小关系为( A )
A.
S1=S2
B.
S1<S2
C.
S1>S2
D.
无法确定
8.如图所示,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( D )
A.-1 B. C. D.
9.如图所示,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG于点E,CF⊥AG于点F,则AE﹣GF的值为( B )
A.1 B. C. D.
10.如图所示,在矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,则四边形PFCG的面积为( D )
A.
5
B.
6
C.
7
D.
8
【解析】如图所示,分别过点P作AD,AB的垂线MN,QR,与矩形ABCD的边分别交于点M,N,Q,R.设PM=x,PQ=y,则由题意可得PN=4-x,PR=6-y.
∵AH=CF=2,AE=CG=3,∴ ,
二、填空题(每题4分,共24分)
11.木工师傅做一个宽60cm,高80cm的矩形木框,为稳固起见,制作时需要在对角顶点间加一根木条,则木条的长为 100 cm.
12.如图所示,在矩形ABCD中,AB=6cm,BC=3cm,E是DC的中点,BF=FC,则四边形DBFE的面积为 6 cm2.
13.如图所示,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠E=__67.5°__.
14.如图所示,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连结BF,DF,则BE:CF的值为 .
15.如图所示,菱形ABCD的两条对角线分别长6和8,P是对角线AC上的一个动点,M,N分别是边AB,BC的中点,则PM+PN的最小值是 5 .
16.如图所示,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=2,则AB= 1+ .
三、解答题(共66分)
17.(6分)在正方形ABCD中,AC为对角线,E为AC上一点,连结EB,ED.求证:∠BEC=∠DEC.
∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA.
在△BEC与△DEC中,∵
∴△BEC≌△DEC(SAS).
∴∠BEC=∠DEC.
18.(8分)如图所示,已知菱形ABCD的对角线交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)若∠E=50° ,求∠BAO的度数.
(1)∵四边形ABCD为菱形,∴AB=CD,AB∥CD.
又∵BE=AB,∴四边形BECD是平行四边形.∴BD=EC.
(2)∵四边形BECD是平行四边形,∴BD∥CE.
∴∠ABO=∠E=50°.
∵在菱形ABCD中,AC⊥BD,∴∠BAO=90°-∠ABO=40°.
19.(8分)如图所示,在□ABCD中,点E,F分别在AB,AD延长线上,使得EF∥BD,连结EF,分别交BC,CD于点P,Q,已知BE=BP.求证:
(1)∠E=∠F.
(2)□ABCD是菱形.
(1)∵BE=BP,∴∠E=∠BPE.
∵四边形ABCD是平行四边形,∴BC∥AD.
∴∠BPE=∠F.∴∠E=∠F.
(2)∵四边形ABCD是平行四边形,∴AB∥DC.∴∠DQF=∠E.
∵∠E=∠F,∠BPE=∠E,∴∠BPE=∠DQF.
∵EF∥BD,∴∠CBD=∠BPE,∠BDC=∠DQF.
∴∠CBD=∠CDB.∴BC=DC.∴□ABCD是菱形.
20.(10分)如图所示,在菱形ABCD中,F为BC边的中点,DF与对角线AC交于点M,过点M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长.
(2)求证AM=DF+ME.
(1)∵四边形ABCD是菱形,∴CB=CD,AB∥CD.∴∠1=∠ACD .
∵∠1=∠2 ,∴∠2=∠ACD .∴MC=MD .
∵ME⊥CD ,∴CD=2CE=2 .∴BC=CD=2.
(2) 延长DF,BA交于点G.
∵四边形ABCD是菱形,∴∠BCA=∠DCA .
∵BC=2CF,CD=2CE,∴CE=CF.
∵CM=CM,∴△CEM≌△CFM. ∴ME=MF.
∵AB∥CD,∴∠2=∠G, ∠GBF=∠BCD.
∵CF=BF,∴△CDF≌△BGF.∴DF=GF.
∵∠1=∠2, ∠G=∠2,∴∠1=∠G.
∴AM=GM=MF+GF=DF+ME.
21.(10分)已知△ABC和△DEF都是边长为10cm的等边三角形,且点B,C,D,E在同一直线上,连结AD,CF.若BD=3cm,△ABC沿着BE的方向以1cm/s的速度运动,设△ABC运动时间为t(s).
(1)当t为何值时,四边形ADFC是菱形.
(2)当t为何值时,四边形ADFC是矩形?并求其面积.
(3)当t为何值时,四边形ADFC的面积是100cm2?
(1)当t=3时,□ADFC是菱形.理由如下:
∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°.∴AC∥DF.
∴四边形ADFC是平行四边形.
当t=3时, B与D重合,∴AD=DF.∴四边形ADFC是菱形.
(2)当t=13时,四边形ADFC是矩形.理由如下:
此时B与E重合,∴AF=CD.又由(1)知四边形ADFC为平行四边形,∴□ADFC是矩形.
∴∠CFD=90°,CF=10cm.
∴S矩形ADFC=10×10=100(cm2).
(3)①B,D重合前,(7﹣t)×5÷2×2=100,解得t=﹣13(不合题意,舍去).
②B,D重合时,t=3,10×5÷2×2≠100(不合题意,舍去).
③B,D重合后,(t+7)×5÷2×2=100,解得t=13.
综上所述,当t为13时,□ADFC的面积是100cm2.
22.(12分)如图所示,∠MON=90°,在∠MON的内部有一个正方形AOCD,点A,C分别在射线OM,ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1.
(1)连结D1D,求证:∠D1DA=90°.
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论.
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1),(2)的结论,再做出一个合理的判断.
(1)∵∠D1AD+∠B1AD=90°,∠OAB1+∠B1AD=90°,
∴∠B1AO=∠D1AD.
∵AD1=AB1,AO=AD,
∴△OAB1≌△DAD1.∴∠D1DA=∠O=90°.
(2)猜想:∠C1CN=45°.
证明:如图1所示,连结C1C,作C1H⊥ON于点H,作C1G⊥CD1于点G,则有C1G=CH.
∵∠C1D1C+∠AD1D=90°,∠C1B1H+∠AB1O=90°,
∴∠C1D1C=∠C1B1H.
∵C1D1=B1C1,∠C1GD1=∠C1HB1=90°,
∴△C1GD1≌△C1 H B1.∴C1G=C1H.
又∵CH=C1G,∴△CHC1是等腰直角三角形.∴∠C1CN=45°.
(3)如图2所示,结论:∠ADD2=90°或∠C2CN=45°均可.
23.(12分)在平面直角坐标系中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC,BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.
(1)当∠BAO=45°时,求点P的坐标.
(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上.
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由.
(1)当∠BAO=45°时,∠PAO=90°,在Rt⊿AOB中,OA=AB=,在Rt⊿APB中,PA=AB=.
∴点P的坐标为.
(2)如图所示,过点P分别作x轴、y轴的垂线,垂足分别为M,N,则有
∠PMA=∠PNB=∠NPM=∠BPA=90°.
∴∠MPA=∠NPB.又PA=PB,
∴△PAM≌△PBN.∴PM=PN.
∴点P在∠AOB的平分线上.
(3)<h≤.当点B与点O重合时,点P到x轴的距离为,然后顶点A在x轴正半轴上向左运动,顶点B在y轴正半轴上向上运动时,点P到x轴的距离逐渐增大,当∠BAO=45°时,PA⊥x轴,这时点P到x轴的距离最大为,然后又逐渐减小到,∵x轴的正半轴、y轴的正半轴都不包含原点O ,∴点P到x轴的距离的取值范围是<h≤.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
