4.2 平行四边形及其性质(1)同步练习
文档属性
| 名称 | 4.2 平行四边形及其性质(1)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-30 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.2 平行四边形及其性质(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
(1)平行四边形的概念:有两组对边分别平 ( http: / / www.21cnjy.com )行的四边形叫做平行四边形.
(2)平行四边形的性质:
①边:平行四边形的对边相等.
②角:平行四边形的对角相等.21·世纪*教育网
基础知识和能力拓展精练
一、选择题
1.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是( ).
A. B. C. D.
2.如图,在平行四边形中,于点,,则等于( ).
( http: / / www.21cnjy.com )
A. B. C. D.
3.如图,平行四边形中,,,于,则等于( ).
( http: / / www.21cnjy.com )
A. B. QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) C. D.
4.如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE 的角度为( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A. 25° B. 35° C. 45° D. 55°
5.平行四边形ABCD中, ∠A:∠B:∠C:∠D的值可以是( )
A. 4:3:3:4 B. 7:5:5:7 C. 4:3:2:1 D. 7:5:7:52-1-c-n-j-y
6.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
( http: / / www.21cnjy.com )
A. 100° B. 95° C. 90° D. 85°
7.如图,平行四边形ABCD周长是28cm,△ABC的周长是22cm,则AC长( )
( http: / / www.21cnjy.com )
A. 14cm B. 12cm C. 10cm D. 8cm
8.如图,在 ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形( )
( http: / / www.21cnjy.com )
A. 6个 B. 7个 C. 8个 D. 9个
二、填空题
9.在□ABCD中,∠B +∠D=200°,则∠A=__________°.
10.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.21*cnjy*com
( http: / / www.21cnjy.com )
11.如图,在平行四边形中,已知,,平分交边于点,则__________.
( http: / / www.21cnjy.com )
12.如图,平行四边形ABCD中,AD=5,AB=3,若AE平分∠BAD交边BC于点E,则线段EC的长度为_____.21cnjy.com
( http: / / www.21cnjy.com )
13.如图,在 ABCD中,E为边CD上一 ( http: / / www.21cnjy.com )点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
三、解答题
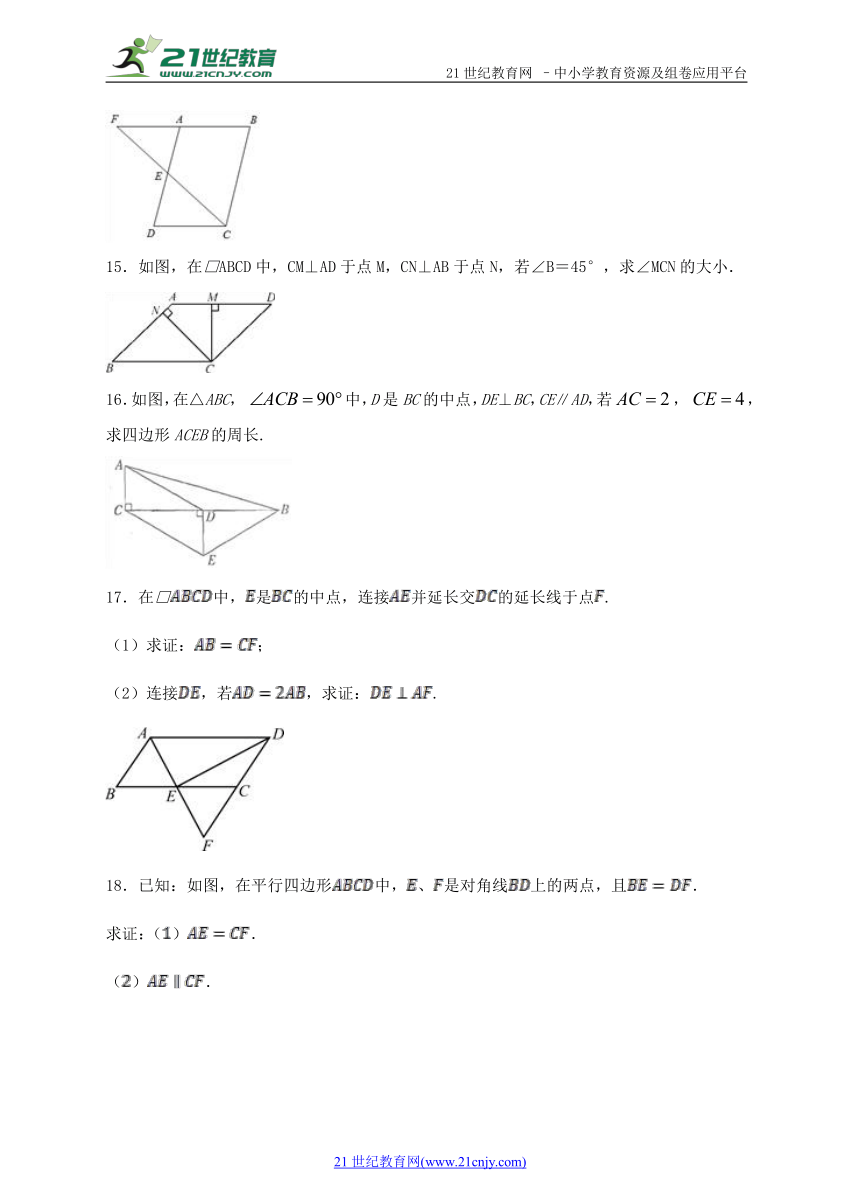
14.如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.【版权所有:21教育】
( http: / / www.21cnjy.com )
15.如图,在□ABCD中,CM⊥AD于点M,CN⊥AB于点N,若∠B=45°,求∠MCN的大小.
( http: / / www.21cnjy.com )
16.如图,在△ABC, 中,D是BC的中点,DE⊥BC,CE∥AD,若, ,求四边形ACEB的周长.【出处:21教育名师】
( http: / / www.21cnjy.com )
17.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
( http: / / www.21cnjy.com )
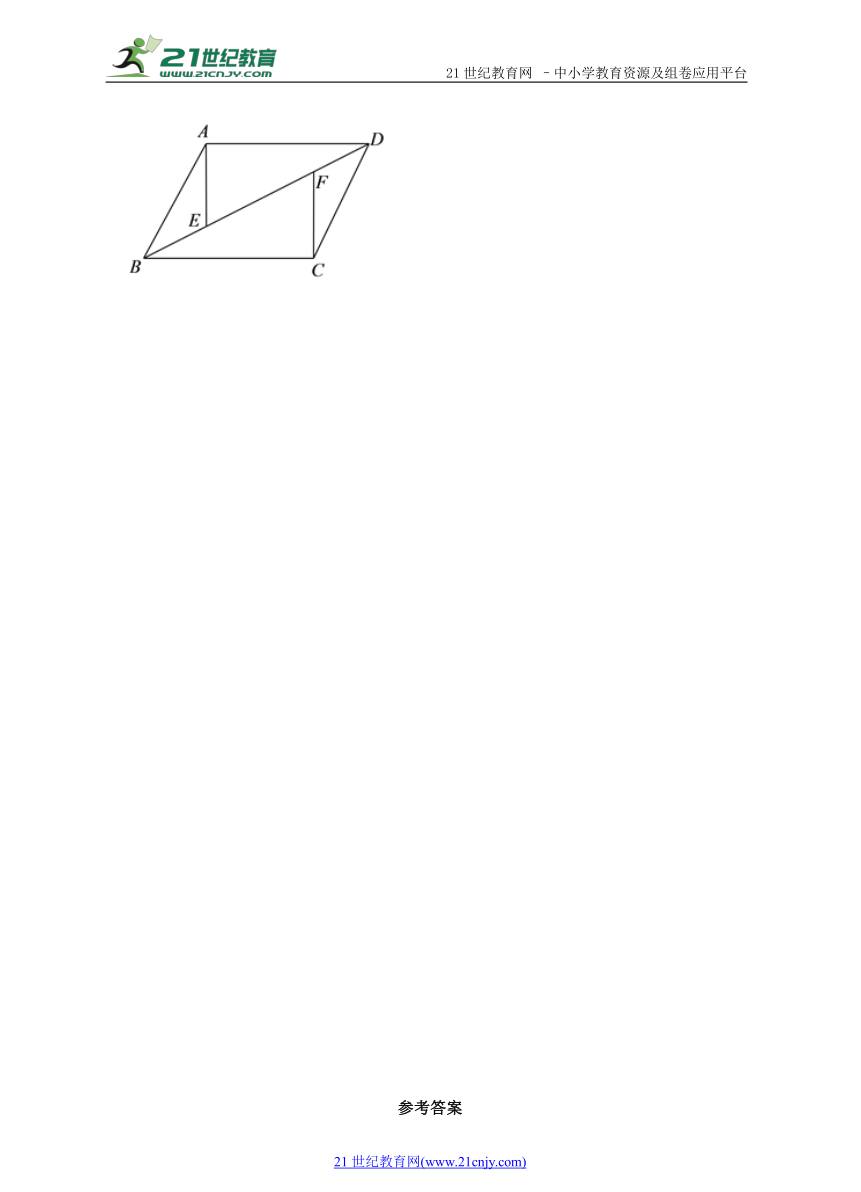
18.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
().
( http: / / www.21cnjy.com )
参考答案
1.B
【解析】∵平行四边形,有两个内角的比为,且这两个内角和为,
∴较小的内角度数为:,
故选.
2.B
【解析】∵,
∴.
∵,
∴.
∵四边形是平行四边形,
∴.
故选.
3.A
【解析】∵,
∴,
∴,
∵平行四边形,
∴,
∴,
∵,
∴,
∴.
故选A.
4.B
【解析】∵平行四边形ABCD,∴∠D=∠B=55°,
∵AE⊥CD,∴∠AED=90°,
∴∠DAE=90°-55°=35°.
故选B.
点睛:本题主要利用平行四边形对角相等解题.
5.D
【解析】试题解析:
( http: / / www.21cnjy.com )
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D,
只有D符合以上两个条件,
故选D.
6.C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
7. D
【解析】根据垂直平分线上点到线段两个端点的距离相等知,EC=AE;
根据在平行四边形ABCD中有BC=AD,AB=CD,
∴△CDE的周长等于CD+DE+CE=CD+DE+AE=CD+AD=AB+BC=3+5=8.
故选B.
8.D
【解析】解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.
∵AD∥EF,CD∥GH,∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有: ABCD, ABHG, ( http: / / www.21cnjy.com )CDGH, BCFE, ADFE, AGOE, BEOH, OFCH, OGDF共9个.即共有9个平行四边形.故选D.21世纪教育网版权所有
9.80
【解析】∵平行四边形ABCD,∴∠B=∠D,
∵∠B +∠D=200°,∴∠B=∠D=100°,
∴∠A=180°-100°=80°.
故答案为80.
点睛:本题关键在于掌握平行四边形的性质.
10.3
【解析】∵四边形ABCD是平行四边形,
∴BC=AD=7cm,CD=AB=4cm,CD∥AB,
∴∠F=∠ABF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠F=∠CBF,
∴CF=BC=7cm,
∴DF=CF-CD=7-4=3(cm).
故答案为:3.
11.3
【解析】如图所示:
( http: / / www.21cnjy.com )
∵平分,
∴.
∵四边形是平行四边形
∴,
∴,
∴.
∵,
∵,
∴.
∵,
∴.
12.2
【解析】∵AE平分∠BAD ( http: / / www.21cnjy.com )交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3,
∴EC=BC-BE=5-3=2,
故答案是:2.www-2-1-cnjy-com
13.36°
【解析】试题分析:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为:36°.
点睛:本题考查了平行四边形的性质、折叠 ( http: / / www.21cnjy.com )的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.
14.12
【解析】试题分析:BF=AB+AF ( http: / / www.21cnjy.com ),由平行四边形的性质可得AB=CD=6,由已知条件不难证明△AEF≌△DEC,所以AF=CD=6,即可得出BF=12.2·1·c·n·j·y
试题解析:
∵E是 ABCD的边AD的中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴AB=CD=6,AB∥CD,
∴∠F=∠DCE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD=6,
∴BF=AB+AF=12.
点睛:本题关键掌握平行四边形的性质、全等三角形的性质及判定.
15.见解析
【解析】试题分析:根据平行四边形的性质得 再利用互余关系可求 用角的和差关系求
试题解析:
∵在 ABCD中,
∵CM⊥AD于M,CN⊥AB于N,
16.10+
【解析】试题分析:首先根据题意得出 ( http: / / www.21cnjy.com )四边形ACED是平行四边形,则DE=AC=2,根据Rt△CDE的勾股定理求出CD的长度,然后根据Rt△ABC的勾股定理得出AB的长度,根据等腰三角形的性质得出BE的长度,从而得出四边形ACEB的周长.21教育网
试题解析:∵ ACB=90,DEBC, ∴ AC//DE,又∵ CE//AD,
∴ 四边形ACED是平行四边形, ∴ DE=AC=2,
在Rt△CDE中,由勾股定理得:CD==2,
∵ D是BC的中点,∴ BC=2CD=4,在Rt△ABC中,由勾股定理得AB==2,
∵ D是BC的中点,DEBC, ∴ EB=EC=4,
∴ 四边形ACEB的周长=AC+CE+EB+BA=10+2.
17.见解析
【解析】试题分析:(1)要证明AB=CF可通 ( http: / / www.21cnjy.com )过△AEB≌△FEC证得,利用平行四边形ABCD的性质不难证明;(2)由平行四边形ABCD的性质可得AB=CD,由△AEB≌△FEC可得AB=CF,所以DF=2CF=2AB,所以AD=DF,由等腰三角形三线合一的性质可证得ED⊥AF .
试题解析:
(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠F,
∵E是BC的中点,
∴BE=CE,
在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS),
∴AB=CF;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=CF,DF=DC+CF ,
∴DF=2CF,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵△AEB≌△FEC,
∴AE=EF,
∴ED⊥AF .
点睛:掌握全等三角形的性质及判定、平行四边形的性质、等腰三角形三线合一的性质.
18.(1)证明见解析(2)证明见解析
【解析】点睛:(1)根据平 ( http: / / www.21cnjy.com )行四边形性质得到AB=CD,AB∥CD,再得到∠ABE=∠CDF,根据“有两边和它们的夹角对应相等的两个三角形全等”得到△ABE≌△CDF,据此可得到即可AE=CF;(2)由△ABE≌△CDF可得∠AEB=∠CFD,再根据“等角的补角相等”得到∠AED=∠CFB,再根据“内错角相等,两直线平行”得到AE∥CF即可.21·cn·jy·com
证明:()∵平行四边形
∴,
.
∴.
在和中,
( http: / / www.21cnjy.com )
∴≌,
∴
( http: / / www.21cnjy.com )
()∵≌,
∴
∴
∴.
点睛:本题考查了平行四边形性质,平行线性质与判定,全等三角形的性质和判定的应用,推出△ABE≌△CDF是解答本题的关键.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.2 平行四边形及其性质(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
(1)平行四边形的概念:有两组对边分别平 ( http: / / www.21cnjy.com )行的四边形叫做平行四边形.
(2)平行四边形的性质:
①边:平行四边形的对边相等.
②角:平行四边形的对角相等.21·世纪*教育网
基础知识和能力拓展精练
一、选择题
1.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是( ).
A. B. C. D.
2.如图,在平行四边形中,于点,,则等于( ).
( http: / / www.21cnjy.com )
A. B. C. D.
3.如图,平行四边形中,,,于,则等于( ).
( http: / / www.21cnjy.com )
A. B. QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) C. D.
4.如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE 的角度为( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A. 25° B. 35° C. 45° D. 55°
5.平行四边形ABCD中, ∠A:∠B:∠C:∠D的值可以是( )
A. 4:3:3:4 B. 7:5:5:7 C. 4:3:2:1 D. 7:5:7:52-1-c-n-j-y
6.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
( http: / / www.21cnjy.com )
A. 100° B. 95° C. 90° D. 85°
7.如图,平行四边形ABCD周长是28cm,△ABC的周长是22cm,则AC长( )
( http: / / www.21cnjy.com )
A. 14cm B. 12cm C. 10cm D. 8cm
8.如图,在 ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形( )
( http: / / www.21cnjy.com )
A. 6个 B. 7个 C. 8个 D. 9个
二、填空题
9.在□ABCD中,∠B +∠D=200°,则∠A=__________°.
10.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.21*cnjy*com
( http: / / www.21cnjy.com )
11.如图,在平行四边形中,已知,,平分交边于点,则__________.
( http: / / www.21cnjy.com )
12.如图,平行四边形ABCD中,AD=5,AB=3,若AE平分∠BAD交边BC于点E,则线段EC的长度为_____.21cnjy.com
( http: / / www.21cnjy.com )
13.如图,在 ABCD中,E为边CD上一 ( http: / / www.21cnjy.com )点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
三、解答题
14.如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.【版权所有:21教育】
( http: / / www.21cnjy.com )
15.如图,在□ABCD中,CM⊥AD于点M,CN⊥AB于点N,若∠B=45°,求∠MCN的大小.
( http: / / www.21cnjy.com )
16.如图,在△ABC, 中,D是BC的中点,DE⊥BC,CE∥AD,若, ,求四边形ACEB的周长.【出处:21教育名师】
( http: / / www.21cnjy.com )
17.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
( http: / / www.21cnjy.com )
18.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
().
( http: / / www.21cnjy.com )
参考答案
1.B
【解析】∵平行四边形,有两个内角的比为,且这两个内角和为,
∴较小的内角度数为:,
故选.
2.B
【解析】∵,
∴.
∵,
∴.
∵四边形是平行四边形,
∴.
故选.
3.A
【解析】∵,
∴,
∴,
∵平行四边形,
∴,
∴,
∵,
∴,
∴.
故选A.
4.B
【解析】∵平行四边形ABCD,∴∠D=∠B=55°,
∵AE⊥CD,∴∠AED=90°,
∴∠DAE=90°-55°=35°.
故选B.
点睛:本题主要利用平行四边形对角相等解题.
5.D
【解析】试题解析:
( http: / / www.21cnjy.com )
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D,
只有D符合以上两个条件,
故选D.
6.C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
7. D
【解析】根据垂直平分线上点到线段两个端点的距离相等知,EC=AE;
根据在平行四边形ABCD中有BC=AD,AB=CD,
∴△CDE的周长等于CD+DE+CE=CD+DE+AE=CD+AD=AB+BC=3+5=8.
故选B.
8.D
【解析】解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.
∵AD∥EF,CD∥GH,∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有: ABCD, ABHG, ( http: / / www.21cnjy.com )CDGH, BCFE, ADFE, AGOE, BEOH, OFCH, OGDF共9个.即共有9个平行四边形.故选D.21世纪教育网版权所有
9.80
【解析】∵平行四边形ABCD,∴∠B=∠D,
∵∠B +∠D=200°,∴∠B=∠D=100°,
∴∠A=180°-100°=80°.
故答案为80.
点睛:本题关键在于掌握平行四边形的性质.
10.3
【解析】∵四边形ABCD是平行四边形,
∴BC=AD=7cm,CD=AB=4cm,CD∥AB,
∴∠F=∠ABF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠F=∠CBF,
∴CF=BC=7cm,
∴DF=CF-CD=7-4=3(cm).
故答案为:3.
11.3
【解析】如图所示:
( http: / / www.21cnjy.com )
∵平分,
∴.
∵四边形是平行四边形
∴,
∴,
∴.
∵,
∵,
∴.
∵,
∴.
12.2
【解析】∵AE平分∠BAD ( http: / / www.21cnjy.com )交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3,
∴EC=BC-BE=5-3=2,
故答案是:2.www-2-1-cnjy-com
13.36°
【解析】试题分析:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为:36°.
点睛:本题考查了平行四边形的性质、折叠 ( http: / / www.21cnjy.com )的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.
14.12
【解析】试题分析:BF=AB+AF ( http: / / www.21cnjy.com ),由平行四边形的性质可得AB=CD=6,由已知条件不难证明△AEF≌△DEC,所以AF=CD=6,即可得出BF=12.2·1·c·n·j·y
试题解析:
∵E是 ABCD的边AD的中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴AB=CD=6,AB∥CD,
∴∠F=∠DCE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD=6,
∴BF=AB+AF=12.
点睛:本题关键掌握平行四边形的性质、全等三角形的性质及判定.
15.见解析
【解析】试题分析:根据平行四边形的性质得 再利用互余关系可求 用角的和差关系求
试题解析:
∵在 ABCD中,
∵CM⊥AD于M,CN⊥AB于N,
16.10+
【解析】试题分析:首先根据题意得出 ( http: / / www.21cnjy.com )四边形ACED是平行四边形,则DE=AC=2,根据Rt△CDE的勾股定理求出CD的长度,然后根据Rt△ABC的勾股定理得出AB的长度,根据等腰三角形的性质得出BE的长度,从而得出四边形ACEB的周长.21教育网
试题解析:∵ ACB=90,DEBC, ∴ AC//DE,又∵ CE//AD,
∴ 四边形ACED是平行四边形, ∴ DE=AC=2,
在Rt△CDE中,由勾股定理得:CD==2,
∵ D是BC的中点,∴ BC=2CD=4,在Rt△ABC中,由勾股定理得AB==2,
∵ D是BC的中点,DEBC, ∴ EB=EC=4,
∴ 四边形ACEB的周长=AC+CE+EB+BA=10+2.
17.见解析
【解析】试题分析:(1)要证明AB=CF可通 ( http: / / www.21cnjy.com )过△AEB≌△FEC证得,利用平行四边形ABCD的性质不难证明;(2)由平行四边形ABCD的性质可得AB=CD,由△AEB≌△FEC可得AB=CF,所以DF=2CF=2AB,所以AD=DF,由等腰三角形三线合一的性质可证得ED⊥AF .
试题解析:
(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠F,
∵E是BC的中点,
∴BE=CE,
在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS),
∴AB=CF;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=CF,DF=DC+CF ,
∴DF=2CF,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵△AEB≌△FEC,
∴AE=EF,
∴ED⊥AF .
点睛:掌握全等三角形的性质及判定、平行四边形的性质、等腰三角形三线合一的性质.
18.(1)证明见解析(2)证明见解析
【解析】点睛:(1)根据平 ( http: / / www.21cnjy.com )行四边形性质得到AB=CD,AB∥CD,再得到∠ABE=∠CDF,根据“有两边和它们的夹角对应相等的两个三角形全等”得到△ABE≌△CDF,据此可得到即可AE=CF;(2)由△ABE≌△CDF可得∠AEB=∠CFD,再根据“等角的补角相等”得到∠AED=∠CFB,再根据“内错角相等,两直线平行”得到AE∥CF即可.21·cn·jy·com
证明:()∵平行四边形
∴,
.
∴.
在和中,
( http: / / www.21cnjy.com )
∴≌,
∴
( http: / / www.21cnjy.com )
()∵≌,
∴
∴
∴.
点睛:本题考查了平行四边形性质,平行线性质与判定,全等三角形的性质和判定的应用,推出△ABE≌△CDF是解答本题的关键.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
