3.4简单几何体的表面展开图课件(第二课时,共35张PPT)
文档属性
| 名称 | 3.4简单几何体的表面展开图课件(第二课时,共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-01 23:13:06 | ||
图片预览






文档简介
课件35张PPT。简单几何体的表面展开图
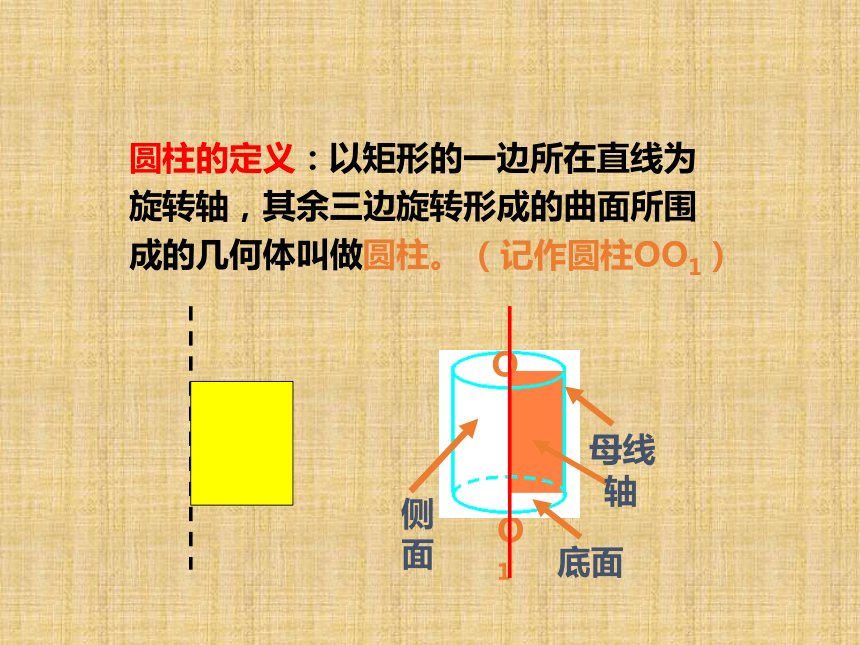
——第二课时新浙教版 九年级下 立方体表面展开图一四一型二三一型二个三型三个二型 对面 “不相连”;异层 “日”字连,整体没有“田”共11种那么怎样得到圆柱、圆锥等简单旋转体的表面展开图呢?O1O圆柱的定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。(记作圆柱OO1)由此可得圆柱的有关概念:
如图,圆柱可以看作矩形ABCD绕边BC所在直线___________,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。
AD旋转所成的面就是圆柱的侧面。
AD不论转到哪个位置,都是圆柱的母线.
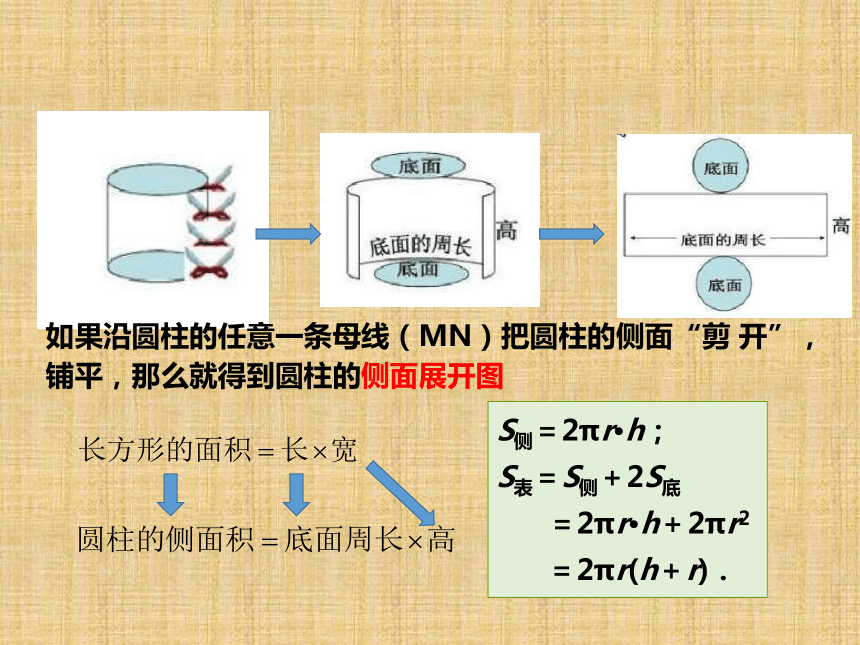
旋转一周如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪 开”,
铺平,那么就得到圆柱的侧面展开图S侧=2πr·h;
S表=S侧+2S底
=2πr·h+2πr2
=2πr(h+r).圆柱的表面展开图:
将圆柱的侧面沿它的一条母线剪开,会得到圆柱的侧面
展开图为矩形,其中一边长等于圆柱的高,另一边长是
底面圆的周长.所以圆柱的侧面积等于 底面圆的周长乘以圆柱的高.
如图,若圆柱的底面半径为r,高为h,
则S侧=2πr·h;
S表=S侧+2S底
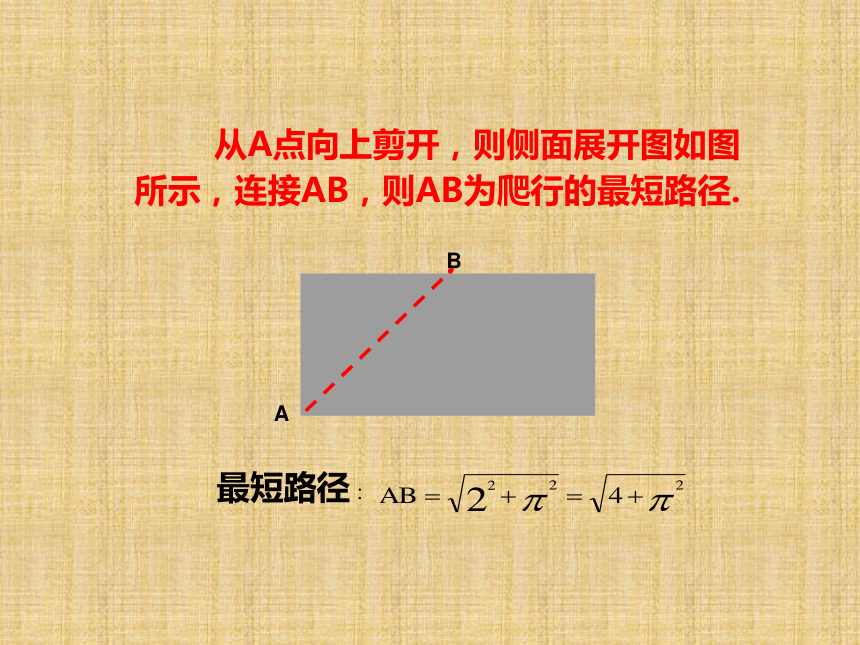
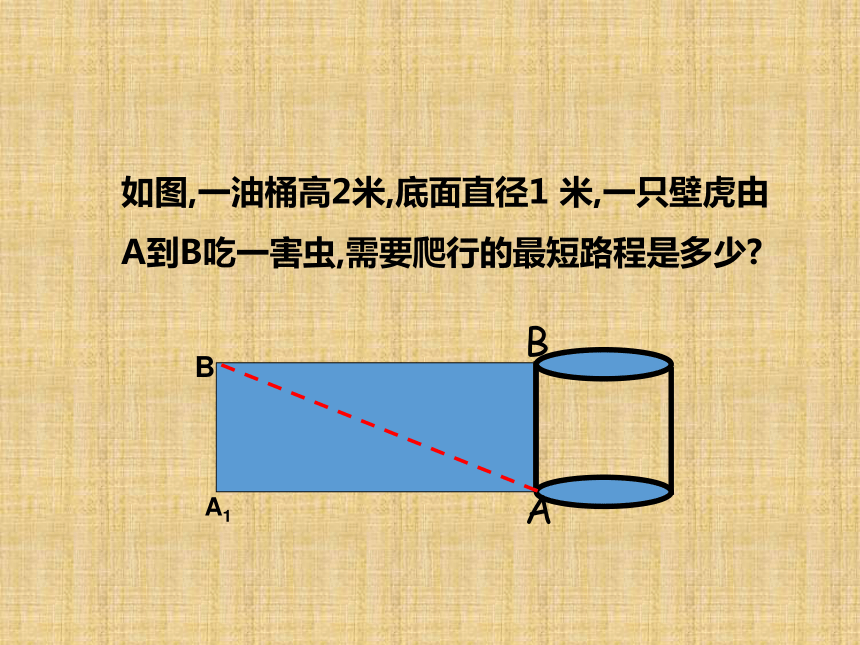
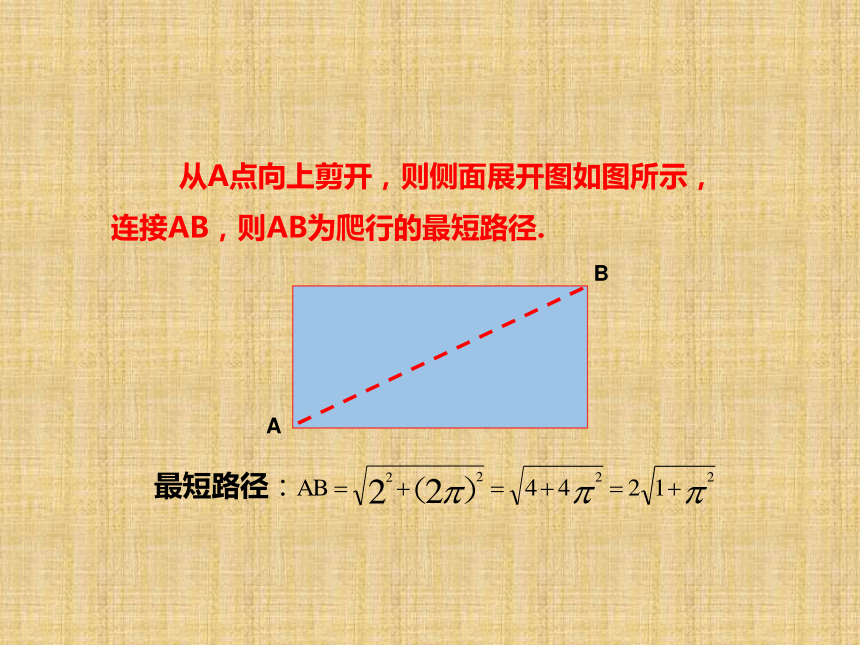
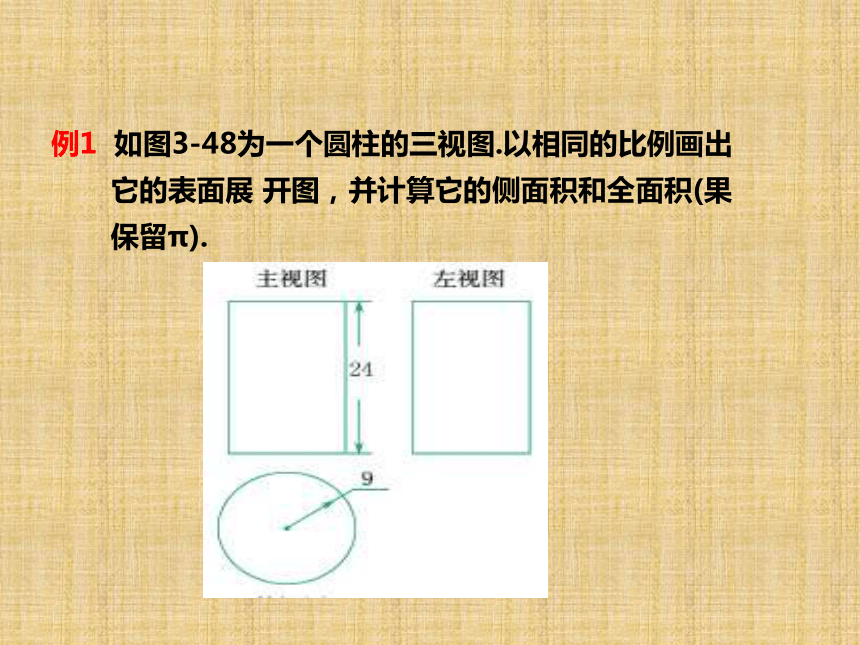
=2πr·h+2πr2=2πr(h+r). 在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,欲从圆柱体的侧面爬行去吃右上角B处的食物,问怎样爬行路径最短,最短路径是多少? 从A点向上剪开,则侧面展开图如图所示,连接AB,则AB为爬行的最短路径.如图,一油桶高2米,底面直径1 米,一只壁虎由A到B吃一害虫,需要爬行的最短路程是多少? 从A点向上剪开,则侧面展开图如图所示,连接AB,则AB为爬行的最短路径.例1 如图3-48为一个圆柱的三视图.以相同的比例画出
它的表面展 开图,并计算它的侧面积和全面积(果
保留π).由图3-48知,圆柱底面圆的半径r为0.9cm,母线长l 为
2.4 cm. 因此圆柱的表面展
开图中两个底面应画成半
径为0.9cm的圆,侧面展开
图应画成长为2πr=2π×0.9
≈5.65(cm),宽为2.4cm的
长方形.
分析:S侧=2πrl=2×π×0.9×2.4=4.32π (cm2);
S全=2πr2+2πrl=2π×0.92+2π×0.9×2.4=5.94π (cm2).
答:这个圆柱的侧面积为4.32πcm2,全面积为5.94πcm2.解:所求圆柱的表面展开,图如图3-49圆锥的定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。OS(记作圆锥SO)1、沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
2、圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?相等母线2、设圆锥的母线长为 l, 底面圆的半径为r, 那么这个扇形的半径 为__ ,扇形的弧长为__ ,因此圆锥的侧面积为___。1、圆锥的侧面展开图是个___。3、圆锥的侧面积与底面积之和称为扇形 l2πrπr l全面积如图,若圆锥的底面半径为r,母线长为l,则
l2=h2+r2
S侧=πrl;
S表=S侧+S底=πrl+πr2=πr(l+r).
若设圆锥的侧面展开图扇形的圆心角为θ,则
θ= ·360°.将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展开图为扇形,其半径等于母线长,弧长是底面圆的周长.圆锥的表面展开图1.弧长的计算公式2.扇形面积计算公式 如图,圆锥的底面半径为1,母线长为4,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少?41B’解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°∴ △ABB’是直角三角形 n=90∵ 圆锥底面半径为1,母线长为4连接BB’,即为蚂蚁爬行的最短路线∴ 2π=已知圆锥底面半径为10cm,母线长为40cm. 求它的侧面展开图的圆心角和全面积ASBAS解:B例2 圆锥形烟囱帽的母线长为80cm,高38.7cm(1)求这个烟囱帽的面积。
(2)以1:40的比例画出这个烟囱帽的展开图解:答:烟囱帽的面积约1、高为4㎝,底面直径为6㎝的圆锥侧面积___
2、圆锥的母线与高的夹角为300,母线长为6cm ,求它的侧面积__,全面积__
3、若圆锥的母线L=10cm,高h=8cm,则其侧面展开图中扇形的圆心角是___
18π27π216° 4.一个圆柱,底面的直径是0.5米,高是1.8米,求它的侧面积。(得数保留两位小数)3.14×0.5×1.8=1.57×1.8(平方米)答:它的侧面积约是2.83平方米。≈2.83 5.圣诞节将近, 某家商店正在制作圣诞节的圆锥形纸帽。已知纸帽的底面周长58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm2) 解:设纸帽的底面半径为rcm,母线长为lcm,所以, 至少要12777.4 cm2的纸。6.如图,已知△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,将△ABC绕直角边AC旋转一周,求所得圆锥的侧面积?ACB解:如果绕AC旋转一周,则所得圆锥的母线为AB=5cm,底面圆半径为BC=4cm,所以所得圆锥的侧面积为:
7. 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?解:将圆锥沿AB展开成扇形ABB’今天我们学习了哪些知识?1、圆柱的表面展开图。2、圆锥的表面展开图。教材87页习题第4、5题。
——第二课时新浙教版 九年级下 立方体表面展开图一四一型二三一型二个三型三个二型 对面 “不相连”;异层 “日”字连,整体没有“田”共11种那么怎样得到圆柱、圆锥等简单旋转体的表面展开图呢?O1O圆柱的定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。(记作圆柱OO1)由此可得圆柱的有关概念:
如图,圆柱可以看作矩形ABCD绕边BC所在直线___________,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。
AD旋转所成的面就是圆柱的侧面。
AD不论转到哪个位置,都是圆柱的母线.
旋转一周如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪 开”,
铺平,那么就得到圆柱的侧面展开图S侧=2πr·h;
S表=S侧+2S底
=2πr·h+2πr2
=2πr(h+r).圆柱的表面展开图:
将圆柱的侧面沿它的一条母线剪开,会得到圆柱的侧面
展开图为矩形,其中一边长等于圆柱的高,另一边长是
底面圆的周长.所以圆柱的侧面积等于 底面圆的周长乘以圆柱的高.
如图,若圆柱的底面半径为r,高为h,
则S侧=2πr·h;
S表=S侧+2S底
=2πr·h+2πr2=2πr(h+r). 在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,欲从圆柱体的侧面爬行去吃右上角B处的食物,问怎样爬行路径最短,最短路径是多少? 从A点向上剪开,则侧面展开图如图所示,连接AB,则AB为爬行的最短路径.如图,一油桶高2米,底面直径1 米,一只壁虎由A到B吃一害虫,需要爬行的最短路程是多少? 从A点向上剪开,则侧面展开图如图所示,连接AB,则AB为爬行的最短路径.例1 如图3-48为一个圆柱的三视图.以相同的比例画出
它的表面展 开图,并计算它的侧面积和全面积(果
保留π).由图3-48知,圆柱底面圆的半径r为0.9cm,母线长l 为
2.4 cm. 因此圆柱的表面展
开图中两个底面应画成半
径为0.9cm的圆,侧面展开
图应画成长为2πr=2π×0.9
≈5.65(cm),宽为2.4cm的
长方形.
分析:S侧=2πrl=2×π×0.9×2.4=4.32π (cm2);
S全=2πr2+2πrl=2π×0.92+2π×0.9×2.4=5.94π (cm2).
答:这个圆柱的侧面积为4.32πcm2,全面积为5.94πcm2.解:所求圆柱的表面展开,图如图3-49圆锥的定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。OS(记作圆锥SO)1、沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
2、圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?相等母线2、设圆锥的母线长为 l, 底面圆的半径为r, 那么这个扇形的半径 为__ ,扇形的弧长为__ ,因此圆锥的侧面积为___。1、圆锥的侧面展开图是个___。3、圆锥的侧面积与底面积之和称为扇形 l2πrπr l全面积如图,若圆锥的底面半径为r,母线长为l,则
l2=h2+r2
S侧=πrl;
S表=S侧+S底=πrl+πr2=πr(l+r).
若设圆锥的侧面展开图扇形的圆心角为θ,则
θ= ·360°.将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展开图为扇形,其半径等于母线长,弧长是底面圆的周长.圆锥的表面展开图1.弧长的计算公式2.扇形面积计算公式 如图,圆锥的底面半径为1,母线长为4,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少?41B’解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°∴ △ABB’是直角三角形 n=90∵ 圆锥底面半径为1,母线长为4连接BB’,即为蚂蚁爬行的最短路线∴ 2π=已知圆锥底面半径为10cm,母线长为40cm. 求它的侧面展开图的圆心角和全面积ASBAS解:B例2 圆锥形烟囱帽的母线长为80cm,高38.7cm(1)求这个烟囱帽的面积。
(2)以1:40的比例画出这个烟囱帽的展开图解:答:烟囱帽的面积约1、高为4㎝,底面直径为6㎝的圆锥侧面积___
2、圆锥的母线与高的夹角为300,母线长为6cm ,求它的侧面积__,全面积__
3、若圆锥的母线L=10cm,高h=8cm,则其侧面展开图中扇形的圆心角是___
18π27π216° 4.一个圆柱,底面的直径是0.5米,高是1.8米,求它的侧面积。(得数保留两位小数)3.14×0.5×1.8=1.57×1.8(平方米)答:它的侧面积约是2.83平方米。≈2.83 5.圣诞节将近, 某家商店正在制作圣诞节的圆锥形纸帽。已知纸帽的底面周长58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm2) 解:设纸帽的底面半径为rcm,母线长为lcm,所以, 至少要12777.4 cm2的纸。6.如图,已知△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,将△ABC绕直角边AC旋转一周,求所得圆锥的侧面积?ACB解:如果绕AC旋转一周,则所得圆锥的母线为AB=5cm,底面圆半径为BC=4cm,所以所得圆锥的侧面积为:
7. 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?解:将圆锥沿AB展开成扇形ABB’今天我们学习了哪些知识?1、圆柱的表面展开图。2、圆锥的表面展开图。教材87页习题第4、5题。
