浙教版九年级下册数学 1.3解直角三角形(3)测试(含答案)
文档属性
| 名称 | 浙教版九年级下册数学 1.3解直角三角形(3)测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 441.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 07:32:09 | ||
图片预览


文档简介
1.3 解直角三角形(第3课时)
如图,在视线与水平线所成的角中,视线在水平线上方的叫做____,视线在水平线下方的叫做____.
在实际测量高度、宽度、距离等问题中,常结合视角知识构造直角三角形,利用三角函数或相似三角形的知识来解决问题.常见的构造的基本图形有如下几种:
(1)如图1,不同地点看同一点;(2)如图2,同一地点看不同点.
A组 基础训练
1.如图,某飞机在空中A点处测得飞行高度h=1000m,从飞机上看到地面指挥站B的俯角α=20°,则地面指挥站与飞机的水平距离约为( )
A.3420m B.9400m C.3640m D.2747m
第1题图
如图,王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
第2题图
A.50m B.100m C.150m D.100m
(衢州中考)如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
第3题图
A.144cm B.180cm C.240cm D.360cm
(苏州中考)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
第4题图
A.4km B.2km C.2km D.(+1)km
5.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图所示),由此可知,B,C两地相距______m.
第5题图
如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________米(结果可保留根号).
第6题图
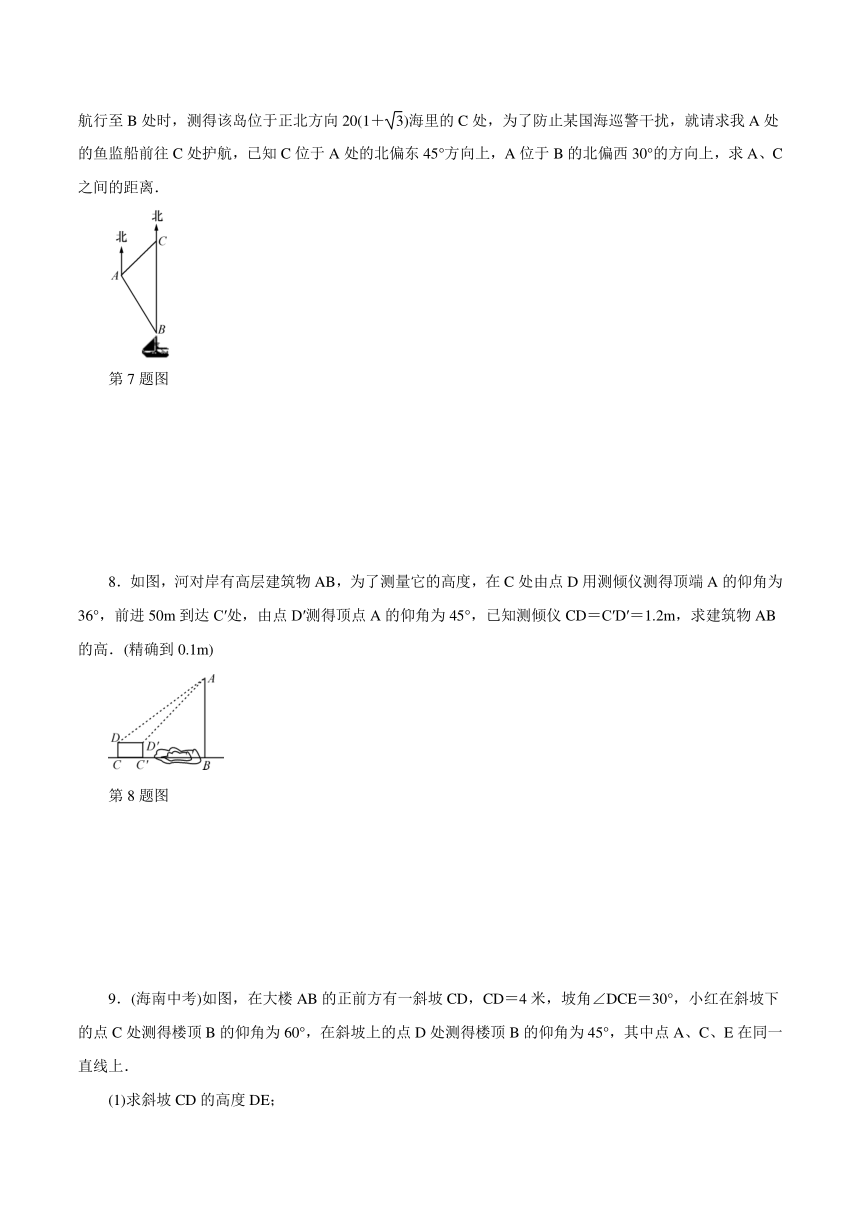
7.(菏泽中考)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
第7题图
8.如图,河对岸有高层建筑物AB,为了测量它的高度,在C处由点D用测倾仪测得顶端A的仰角为36°,前进50m到达C′处,由点D′测得顶点A的仰角为45°,已知测倾仪CD=C′D′=1.2m,求建筑物AB的高.(精确到0.1m)
第8题图
9.(海南中考)如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号).
第9题图
B组 自主提高
10.(台州中考)如图,这是一把可调节座椅的侧面示意图,已知头枕上的点到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少cm?(结果取整数)
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
第10题图
11.如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5km处是村庄M;在点A北偏东53.5°方向上,距离10km处是村庄N.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求M,N两村之间的距离;
(2)要在公路AB旁修建一个土特产收购站P,使得M,N两村到P的距离之和最短,求这个最短距离.
第11题图
参考答案
1.3 解直角三角形(第3课时)
【课堂笔记】
仰角 俯角
【课时训练】
1-4.DDBC 5.200 6.(7+21) 7.如图,作AD⊥BC,垂足为D,
第7题图
由题意得,∠ACD=45°,∠ABD=30°.设CD=x,在Rt△ACD中,可得AD=x,在Rt△ABD中,可得BD=x,又∵BC=20(1+),CD+BD=BC,即x+x=20(1+),解得:x=20,∴AC=x=20(海里).答:A、C之间的距离为20海里. 8.延长DD′交AB于点E,设AE=x,在Rt△ADE中,DE==,在Rt△AD′E中,D′E==,∵DD′=DE-D′E,∴-=50,∴x≈132.84,∴AB=AE+EB=134.0m. 9.(1)在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,∴DE=DC=2米; (2)过D作DF⊥AB,交AB于点F,∵∠BFD=90°,∠BDF=45°,∴∠DBF=45°,即△BFD为等腰直角三角形,设BF=DF=x米,∵四边形DEAF为矩形,∴AF=DE=2米,即AB=(x+2)米,在Rt△ABC中,∠ABC=30°,
第9题图
∴BC====米,BD=BF=x米,DC=4米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°,在Rt△BCD中,根据勾股定理得:2x2=+16,解得:x=4+4(负值舍去),则AB=(6+4)米.
如图,过点A′作A′H⊥OA于点H,由旋转可知,OA′=OA=80,在Rt△OA′H中,OH=OA′cos35°≈80×0.82=65.6.∴AH=OA-OH=80-65.6=14.4≈14cm.答:调整后点A′比调整前点A的高度降低了14cm.
第10题图
(1)过点M作CD∥AB,过点N作NE⊥AB于点E,如图.在Rt△ACM中,∠CAM=36.5°,AM=5km,∵sin36.5°==0.6,∴CM=3,AC==4(km).在Rt△ANE中,∠NAE=90°-53.5°=36.5°,AN=10km,∵sin36.5°==0.6,∴NE=6,AE==8(km),∴MD=CD-CM=AE-CM=5(km),ND=NE-DE=NE-AC=2(km),在Rt△MND中,MN==(km); (2)作点N关于AB的对称点G,连结MG交AB于点P,点P即为站点,此时PM+PN=PM+PG=MG,在Rt△MDG中,MG===5(km).答:最短距离为5km.
第11题图
如图,在视线与水平线所成的角中,视线在水平线上方的叫做____,视线在水平线下方的叫做____.
在实际测量高度、宽度、距离等问题中,常结合视角知识构造直角三角形,利用三角函数或相似三角形的知识来解决问题.常见的构造的基本图形有如下几种:
(1)如图1,不同地点看同一点;(2)如图2,同一地点看不同点.
A组 基础训练
1.如图,某飞机在空中A点处测得飞行高度h=1000m,从飞机上看到地面指挥站B的俯角α=20°,则地面指挥站与飞机的水平距离约为( )
A.3420m B.9400m C.3640m D.2747m
第1题图
如图,王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
第2题图
A.50m B.100m C.150m D.100m
(衢州中考)如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
第3题图
A.144cm B.180cm C.240cm D.360cm
(苏州中考)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
第4题图
A.4km B.2km C.2km D.(+1)km
5.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图所示),由此可知,B,C两地相距______m.
第5题图
如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________米(结果可保留根号).
第6题图
7.(菏泽中考)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
第7题图
8.如图,河对岸有高层建筑物AB,为了测量它的高度,在C处由点D用测倾仪测得顶端A的仰角为36°,前进50m到达C′处,由点D′测得顶点A的仰角为45°,已知测倾仪CD=C′D′=1.2m,求建筑物AB的高.(精确到0.1m)
第8题图
9.(海南中考)如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号).
第9题图
B组 自主提高
10.(台州中考)如图,这是一把可调节座椅的侧面示意图,已知头枕上的点到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少cm?(结果取整数)
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
第10题图
11.如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5km处是村庄M;在点A北偏东53.5°方向上,距离10km处是村庄N.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求M,N两村之间的距离;
(2)要在公路AB旁修建一个土特产收购站P,使得M,N两村到P的距离之和最短,求这个最短距离.
第11题图
参考答案
1.3 解直角三角形(第3课时)
【课堂笔记】
仰角 俯角
【课时训练】
1-4.DDBC 5.200 6.(7+21) 7.如图,作AD⊥BC,垂足为D,
第7题图
由题意得,∠ACD=45°,∠ABD=30°.设CD=x,在Rt△ACD中,可得AD=x,在Rt△ABD中,可得BD=x,又∵BC=20(1+),CD+BD=BC,即x+x=20(1+),解得:x=20,∴AC=x=20(海里).答:A、C之间的距离为20海里. 8.延长DD′交AB于点E,设AE=x,在Rt△ADE中,DE==,在Rt△AD′E中,D′E==,∵DD′=DE-D′E,∴-=50,∴x≈132.84,∴AB=AE+EB=134.0m. 9.(1)在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,∴DE=DC=2米; (2)过D作DF⊥AB,交AB于点F,∵∠BFD=90°,∠BDF=45°,∴∠DBF=45°,即△BFD为等腰直角三角形,设BF=DF=x米,∵四边形DEAF为矩形,∴AF=DE=2米,即AB=(x+2)米,在Rt△ABC中,∠ABC=30°,
第9题图
∴BC====米,BD=BF=x米,DC=4米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°,在Rt△BCD中,根据勾股定理得:2x2=+16,解得:x=4+4(负值舍去),则AB=(6+4)米.
如图,过点A′作A′H⊥OA于点H,由旋转可知,OA′=OA=80,在Rt△OA′H中,OH=OA′cos35°≈80×0.82=65.6.∴AH=OA-OH=80-65.6=14.4≈14cm.答:调整后点A′比调整前点A的高度降低了14cm.
第10题图
(1)过点M作CD∥AB,过点N作NE⊥AB于点E,如图.在Rt△ACM中,∠CAM=36.5°,AM=5km,∵sin36.5°==0.6,∴CM=3,AC==4(km).在Rt△ANE中,∠NAE=90°-53.5°=36.5°,AN=10km,∵sin36.5°==0.6,∴NE=6,AE==8(km),∴MD=CD-CM=AE-CM=5(km),ND=NE-DE=NE-AC=2(km),在Rt△MND中,MN==(km); (2)作点N关于AB的对称点G,连结MG交AB于点P,点P即为站点,此时PM+PN=PM+PG=MG,在Rt△MDG中,MG===5(km).答:最短距离为5km.
第11题图
