5.1 矩形（1）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.1 矩形（1）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
矩形的性质
①平行四边形的性质矩形都具有；
②角：矩形的四个角都是直角；
③边：邻边垂直；
④对角线：矩形的对角线相等；
⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．
基础知识和能力拓展训练
一、选择题
1．矩形的两条对角线的一个交角为60°，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为（ ）
A. 10cm B. 5cm C. 6cm D. 8cm
2．如图，将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点上，若AB＝6，BC＝9，则BF的长为（ ）。
A. 4 B. 32 C. 4.5 D. 5
3．如图所示，四边形ABCD为矩形，点O为对角线的交点，∠BOC=120°，AE⊥BO交BO
于点E，AB=4，则BE等于（　　）
A. 1 B. 2 C. 3 D. 4
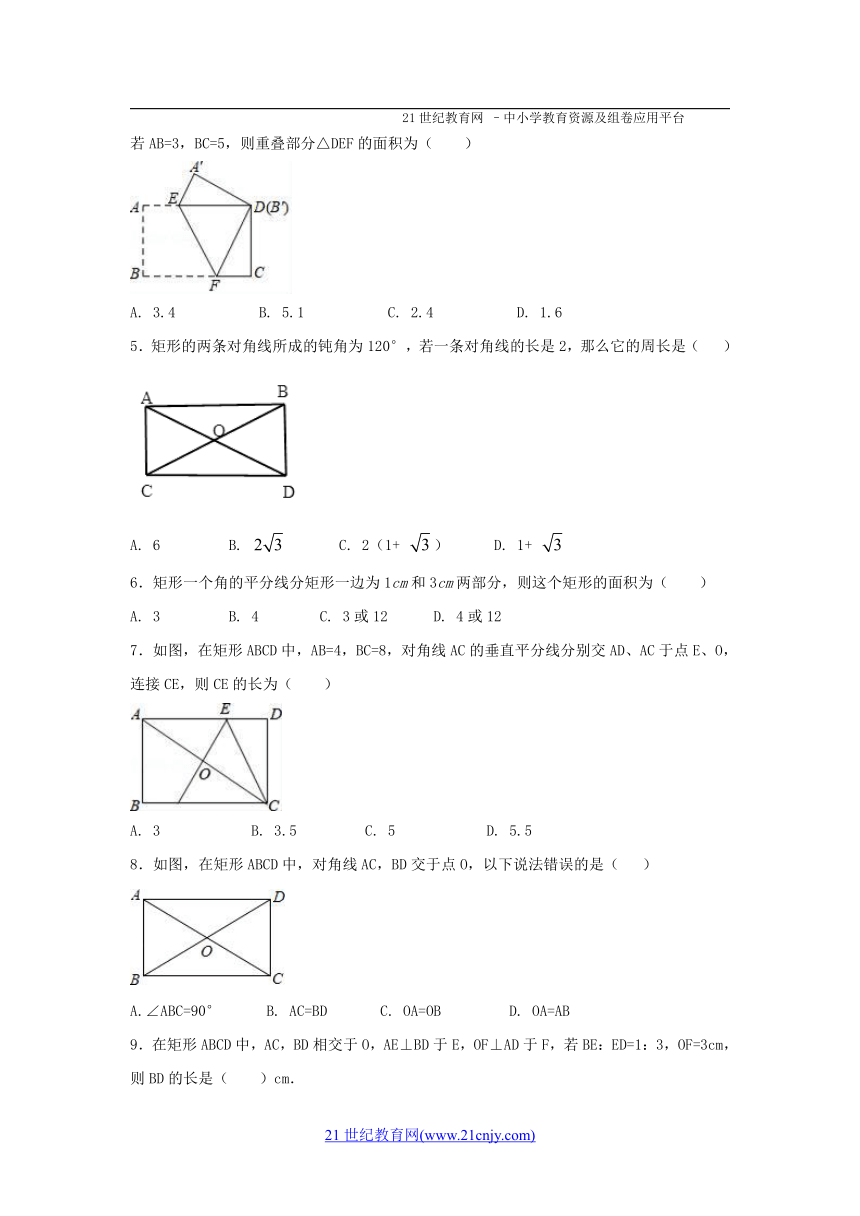
4．如图，把一张矩形纸片ABCD按如图所示方式折叠，使得顶点B和D重合，折痕为EF，若AB=3，BC=5，则重叠部分△DEF的面积为（　　）
A. 3.4 B. 5.1 C. 2.4 D. 1.6
5．矩形的两条对角线所成的钝角为120°，若一条对角线的长是2，那么它的周长是（ ）
A. 6 B. C. 2（1+ ） D. 1+
6．矩形一个角的平分线分矩形一边为1cm和3cm两部分，则这个矩形的面积为（ ）
A. 3 B. 4 C. 3或12 D. 4或12
7．如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（　　）
A. 3 B. 3.5 C. 5 D. 5.5
8．如图，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是（ ）
A.∠ABC=90° B. AC=BD C. OA=OB D. OA=AB
9．在矩形ABCD中，AC，BD相交于O，AE⊥BD于E，OF⊥AD于F，若BE：ED=1：3，OF=3cm，则BD的长是（　　）cm．
A. 6 B. 8 C. 10 D. 12
10．矩形ABCD中， O是BC的中点，∠AOD＝90°．矩形的周长为20cm ，则AB的长为（ ）
A. 1cm B. 2cm C. 2.5cm D. cm
二、填空题
11．矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AC+BD=16，则该矩形的面积为________
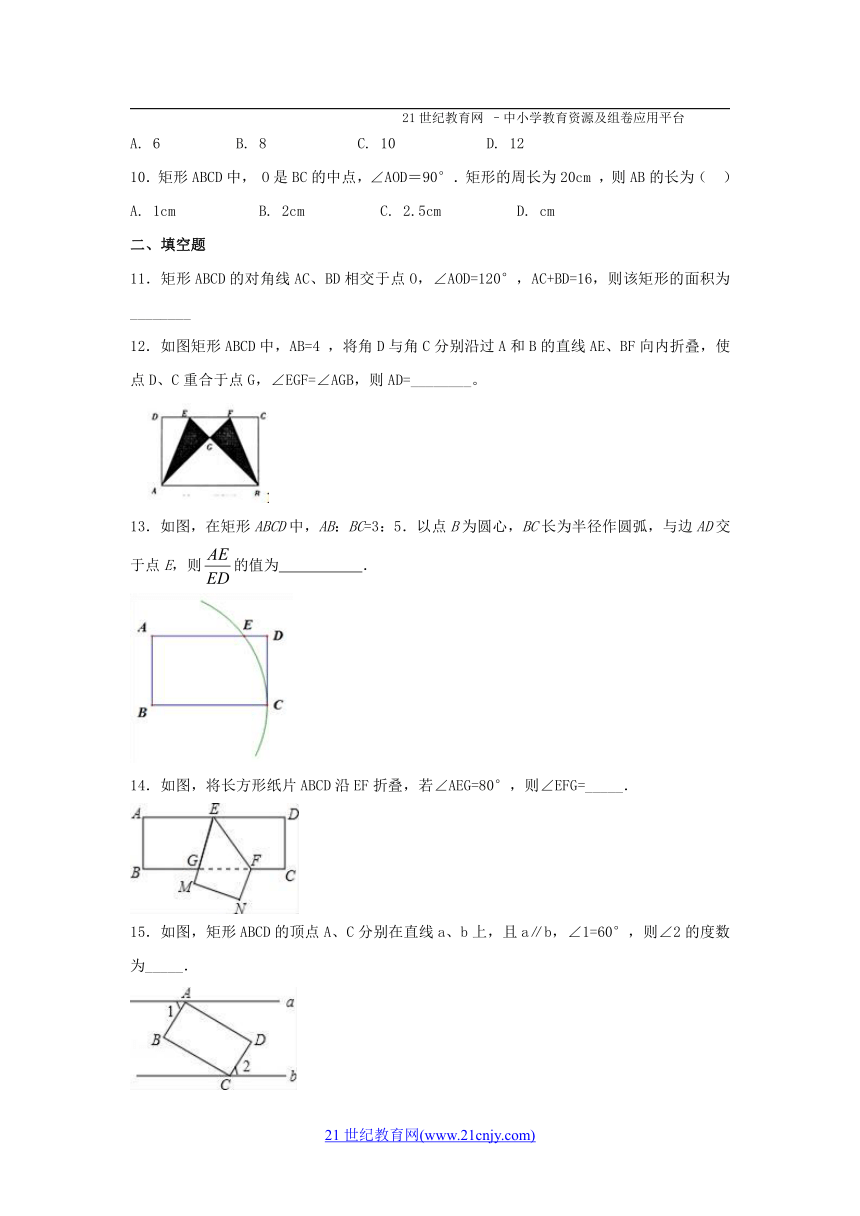
12．如图矩形ABCD中，AB=4 ，将角D与角C分别沿过A和B的直线AE、BF向内折叠，使点D、C重合于点G，∠EGF=∠AGB，则AD=________。
13．如图，在矩形ABCD中，AB：BC=3：5．以点B为圆心，BC长为半径作圆弧，与边AD交于点E，则的值为 ．
14．如图，将长方形纸片ABCD沿EF折叠，若∠AEG=80°，则∠EFG=_____．
15．如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为_____．
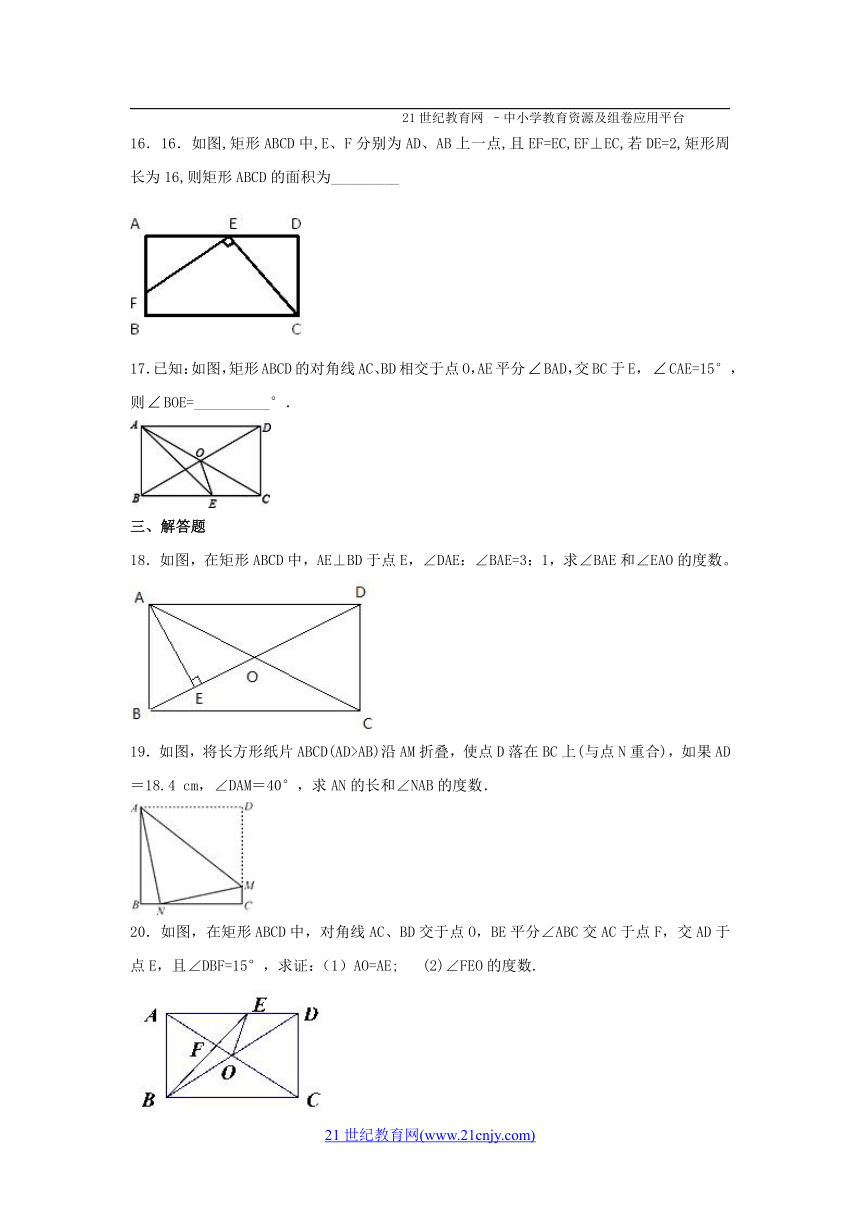
16．16．如图,矩形ABCD中,E、F分别为AD、AB上一点,且EF=EC,EF⊥EC,若DE=2,矩形周长为16,则矩形ABCD的面积为_________
17．已知：如图，矩形ABCD的对角线AC、BD相交于点O，AE平分BAD，交BC于E， CAE=15°，则BOE=__________°．
三、解答题
18．如图，在矩形ABCD中，AE⊥BD于点E，∠DAE：∠BAE=3：1，求∠BAE和∠EAO的度数。
19．如图，将长方形纸片ABCD(AD>AB)沿AM折叠，使点D落在BC上(与点N重合)，如果AD＝18.4 cm，∠DAM＝40°，求AN的长和∠NAB的度数．
20．如图，在矩形ABCD中，对角线AC、BD交于点O，BE平分∠ABC交AC于点F，交AD于点E，且∠DBF=15°，求证：（1）AO=AE; (2)∠FEO的度数.
21．如图，矩形ABCD中，AD=8，CD=6，△CED沿边CE翻折后D恰好落在对角线BD上的D’处，求CE的长.
22．如图，在矩形ABCD中，点E．点F在BC边上，且BE=CF，AF，DE交于点M．求证：
①△ABF≌△DCE
②AM=DM．
23．如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2 cm/s的速度向D移动．
（1）P、Q两点从出发开始到几秒？四边形PBCQ的面积为33cm2；
（2）P、Q两点从出发开始到几秒时？点P和点Q的距离是10cm．
参考答案
1．B
【解析】如图，由题意可知，在矩形ABCD中，AC+BD=10cm，∠AOB=60°，
∴AC=BD=10cm，
∴AO=BO=5cm，
∴△AOB是等边三角形，
∴AB=AO=5cm.
故选B.
2．A
【解析】试题分析：根据题意可知：BC′=3，设BF=x，则CF=(9－x)，根据折叠可得：C′F= CF=(9－x)，根据Rt△BFC′的勾股定理可得： ，解得：x=4，故选A．
3．B
【解析】∵四边形ABCD为矩形，
∴OA=OB=OC=OD，
∵∠BOC=120°，
∴∠AOB=180°-120°=60°，
∴△AOB为等边三角形，即AO=BO=AB=4，
∵AE⊥BO，
∴BE=BO=2.
故选B．
点睛：本题考查了矩形的性质、等边三角形的判定及性质，判定出△AOB为等边三角形是解题的关键．
4．B
【解析】由折叠知，AE=A’E，AB=A’D=3．
设DE=x,则AE= A’E =5-x，CF=4-x，
在Rt△A’EF中，利用勾股定理得：x2=(5-x)2+32，
解得：x=3.4.
∴△DEF的面积为： .
故选B.
5．C
【解析】解：如图．∵四边形ABCD是矩形，∴AC=BD=2，AO=OC=AC，OB=DO=BD，∴OA=OB=1．∵∠AOB=180°﹣120°=60°，∴△AOB是等边三角形，∴AO=OB=AB=1，∴AO=OB=AB=1，∴AD==，∴CD=AB=1，BC=AD=，∴它的周长是：2（1+）．故选C．
6．D
【解析】试题解析：
∵四边形ABCD是矩形，
∴AB=CD，AD=BC，AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠AEB=∠ABE，
∴AB=AE，
①当AE=1cm时，AB=1cm=CD，AD=1cm+3cm=4cm=BC，
此时矩形的面积是1cm×4cm=4cm2；
②当AE=3cm时，AB=3cm=CD，AD=4cm=BC，
此时矩形的面积是：3cm×4cm=12cm2；
故选D.
7．C
【解析】∵四边形ABCD是矩形，
∴CD=AB=4，AD=BC=8，
∵EO是AC的垂直平分线，
∴AE=CE，
设CE=x，则ED=AD﹣AE=8﹣x，
在Rt△CDE中，CE2=CD2+ED2，
即x2=42+（8﹣x）2，
解得：x=5，
即CE的长为5．
故选：C．
【点睛】考查了矩形的性质、勾股定理、线段垂直平分线上的点到线段两端点的距离相等的性质；熟练掌握勾股定理，把相应的边转化为同一个直角三角形的边是解题的关键．
8．D
【解析】解：∵四边形ABCD是矩形，∴∠ABC=90°，AC=BD，OA=OC，OB=OD，∴OA=OB，故A、B、C正确，故错误的是D．故选D．
9．D
【解析】试题解析：∵ABCD是矩形，
∴BO=OD=OA．
∵BE：ED=1：3，
∴BE=EO．
又AE⊥BD，
∴OB=OA=AB．
∴∠ABD=60°．
∴∠FDO=30°
∵OF⊥AD，OF=3，
∴OD=6．
∴BD=2 OD=12．故选D．
10．D
【解析】解：∵O是BC中点，∴OB=OC．∵四边形ABCD是矩形，∴AB=DC，∠B=∠C=90°．在△ABO和△DCO中，∵，∴△ABO≌△DCO（SAS），∴∠AOB=∠DOC．∵∠AOD=90°，∴∠AOB=∠DOC=45°，∴∠BAO=45°=∠AOB，∴AB=OB，BC=2AB．∵矩形ABCD的周长是20cm，∴2（AB+BC）=20cm，AB+BC=10cm，∴3AB=10cm，∴AB=cm．故选D．
点睛：本题考查了矩形性质、全等三角形的性质和判定，等腰直角三角形性质的应用，关键是求出AB=OB，题目比较好，难度适中．
11．16
【解析】解：如图．∵四边形ABCD是矩形，∴AC=BD．又AC+BD=16，∴AC=BD=8，且OA=OB=4．
∵∠AOD=120°，可得∠AOB=60°，∴△AOB是等边三角形，∴AB=4．∵∠ABC=90°，∴∠ACB=30°，∴BC==4，∴矩形的面积=4×4=16．故答案为：16．
12．
【解析】由折叠的性质知，AD=AG=BG=BC，∠D=∠C=∠EGA=∠FGB=90°．
∵∠EGF=∠AGB,
∴∠EGA+∠FGB+∠EFG+∠AGB=360°，
∴∠EGF=∠AGB=90°，
∴△GAB是等腰直角三角形，
∴AG=BG,
∵AG2+BG2=AB2,
∴AG=AB，
∴AD=AG=×4=2．
13．4
【解析】解：如图，连接BE，则BE=BC．
设AB=3x，BC=5x．∵四边形ABCD是矩形，∴AB=CD=3x，AD=BC=5x，∠A=90°，由勾股定理得：AE=4x，则DE=5x﹣4x=x，∴．故答案为：4．
点睛：本题考查了矩形的性质，勾股定理的应用，解答此题的关键是求出x的值，题目比较好，难度适中．
14．50°
【解析】试题解析：∵把一张长方形纸片ABCD沿EF折叠,
∴ ∠DEF=∠FEM,
∴
∵AD∥BC，
∴
故答案为：
15．60°
【解析】延长AB交直线b于点E，
∵a∥b，
∴∠AEC=∠1=60°，
∵四边形ABCD是矩形，
∴AB∥CD，
∴∠2=∠AEC=60°，
故答案为：60°.
【点睛】本题考查了矩形的性质，平行线的性质，准确作出辅助线是解题的关键.
16．15
【解析】因为EF⊥EC，所以∠FEC=90°，所以∠AEF+∠DEC=90°，因为∠AEF+∠AFE=90°，所以∠AFE=∠DEC，因为∠A=∠D，EF=CE，所以△AEF≌△DCE，所以AE=CD，AF=DE，设AB=CD=x，则AD=AE+DE=CD+DE=x+2，所以2（x+x+2）=16,解得x=3，所以AB×BC=3×（3+2）=15，故答案为15.
17．75
【解析】因为AE平分BAD，所以∠BAE=45°，因为∠ABE=90°，所以∠AEB=45°，因为∠CAE=15°，所以∠OAB=60°，因为四边形ABCD是矩形，所以OA=OB，所以△OAB是等边三角形，所以∠OBA=60°，OB=BA，所以∠OBE=30°，OB=BE，所以∠BOE=∠BEO=×(180°-30°)=75°，故答案为75°.
18．∠BAE=22.5°, ∠EAO=45°.
【解析】试题分析：根据矩形性质得出 推出 求出求出 即可求出的度数．
试题解析：∵四边形ABCD是矩形，
∴
∴OA=OB，
∵∠DAE:∠BAE=3:1，
∴
∵AE⊥BD，
∴
∴
∵OA=OB，
∴
∴
19．见解析
【解析】试题分析：依据翻折的性质可知AN=AD，∠DAM=∠NAM，于是可求得问题的答案．
试题解析：解：由翻折的性质可知：AN=AD=18.4cm，∠DAM=∠NAM=40°，∴∠BAN=90°﹣40°﹣40°=10°．
20．见解析
【解析】试题分析：（1）根据矩形的得出OB=OA，∠ABC=∠BAD=90°，求出∠EBA=45°，可得AB=AE；求出∠OBA=60°，得出等边△OBA，推出BA=OA，从而AO=AE；
（2）由△OBA是等边三角形得∠BAO=60°，从而∠OAE=30°，然后根据等腰三角形的性质可求出∠AEO的度数，进而可求出∠FEO的度数.
解：∵四边形ABCD是矩形，
∴∠ABC=∠BAD=90°，OB=OA，
∵BE平分∠ABC，
∴∠ABE=45°，
∵∠OBF=15°，
∴∠OBA=60°，
∵OB=OA，
∴△BOA是等边三角形，
∴∠OAB=60°，BA=OA，
∴∠OEF=∠BEA=180°-∠OAB-∠EBA=180°-45°-60°=75°，
∵∠BAF=90°，∠FBA=45°，
∴∠FBA=45°=∠BFA，
∴BA=AE，
∴AO=AE；
（2）∵∠BAD=90°，∠OAB=60°，
∴∠OAF=90°-60°=30°，
∴∠AEO=×（180°-30°）=75°，
∴∠AOF=∠OEF=75°，
∴∠FEO=75°-45°=30°．
点睛：本题考查了矩形的性质，等边三角形的性质和判定，等腰直角三角形，等腰三角形的性质和判定的应用，解此题的关键是熟练掌握矩形的性质和等腰三角形的判定与性质，题目综合性比较强，有一定的难度．
21．CE=
【解析】整体分析：
由翻折（轴对称）的性质证明△CDE∽△ABD，求出DE，再在Rt△CDE中角勾股定理求结论.
解：由翻折知：DE=D′E，∠ADC=∠CD′=90°，CD=CD′，△CDE≌△CD′，
所以CE⊥DD′，∠CD′D=∠CDD′∠ABD，∠ADB=∠ECD′
所以△CDE∽△ABD，
所以=，即ED=，
因为CE2=62+()2=36+=，
所以CE=.
22．见解析
【解析】整体分析：
①用SAS证明△ABF≌△DCE；（2）由△ABF≌△DCE得∠AFB=∠DEC，再结合AD∥BC，得∠MAD=∠MDA，用等角对等边证明MA=MD.
证明：①∵四边形ABCD为矩形，
∴AB=DC，∠B=∠C，
∵BE=CF，
∴BE+EF=EF+CF，即BF=CE，
在△ABF和△DCE中
∴△ABF≌△DCE（SAS）；
②∵△ABF≌△DCE，
∴∠AFB=∠DEC，
∵AD∥BC，
∴∠AFB=∠MAD，∠DEC=∠MDA，
∴∠MAD=∠MDA，
∴MA=MD．
23．（1）x=5；（2）t=4.8或1.6．
【解析】解：（1）设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2，
则PB=（16﹣3x）cm，QC=2xcm，
根据梯形的面积公式得（16﹣3x+2x）×6=33，
解之得x=5，
（2）设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，
作QE⊥AB，垂足为E，
则QE=AD=6，PQ=10，
∵PA=3t，CQ=BE=2t，
∴PE=AB﹣AP﹣BE=|16﹣5t|，
由勾股定理，得（16﹣5t）2+62=102，
解得t1=4.8，t2=1.6．
答：（1）P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2；
（2）从出发到1.6秒或4.8秒时，点P和点Q的距离是10cm．
【点睛】（1）根据梯形的面积公式可列方程： 求解；
（2）作QE⊥AB，垂足为E，在RtPEQ中，用勾股定理列方程求解．
21世纪教育网(www.21cnjy.com)