5.3 正方形（1）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.3 正方形（1）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
正方形的判定方法：
①先判定四边形是矩形，再判定这个矩形有一组邻边相等；
②先判定四边形是菱形，再判定这个菱形有一个角为直角．
③还可以先判定四边形是平行四边形，再用1或2进行判定．
基础知识和能力拓展训练
一、选择题
1．在下列命题中，正确的是(　　)
A. 有一组对边平行的四边形是平行四边形 B. 有一组邻边相等的平行四边形是菱形
C. 有一个角是直角的四边形是矩形 D. 对角线互相垂直平分的四边形是正方形
2．下列命题中，真命题是（ ）
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线相等的四边形是矩形
3．小明在学习了正方形之后，给同桌小文出了错题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使 ABCD为正方形（如图所示），现有如下四种选法，你认为其中错误的是（　　）
A. ①② B. ①③ C. ②③ D. ②④
4．如图，要证明平行四边形ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明（ ）
A. AB＝AD且AC⊥BD B. AB＝AD且AC＝BD
C. ∠A＝∠B且AC＝BD D. AC和BD互相垂直平分
5．矩形各内角的平分线若能围成一个四边形，则这个四边形一定是（ ）
A. 平行四边形 B. 矩形 C. 正方形 D. 菱形
6．如图，在四边形ABCD中,点O是对角线的交点，能判定这个四边形是正方形的是（ ）
A. AC=BD，AB∥CB，AD∥BC B. AD∥BC，∠BAD =∠BCD
C. AO=CO，BO=DO，AB=BC D. AO=BO=CO=DO，AC⊥BD
7．如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点, 且∠ACB=(　 　)时,则四边形AECF是正方形.
A. 30° B. 45° C. 60° D. 90°
二、填空题
8．已知矩形ABCD，当满足条件______ 时，它成为正方形填一个你认为正确的条件即可．
9．顺次连接四边形各边中点，所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。
10．(2017·齐齐哈尔中考)矩形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件________________，使其成为正方形(只填一个即可)．
11．如图，在△ABC中，点D，E，F分别是△ABC的边AB，BC，AC上的点，且DE∥AC，EF∥AB，要使四边形ADEF是正方形，还需添加条件：__________________．
12．如图在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF,请你添加一个条件_________________，使四边形BECF是正方形.
13．如图，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是____________．(补充一个即可)
14．对角线_______________________________________的四边形是正方形.
15．如图，在△ABC中，O是AC上一动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F.若点O运动到AC的中点，则∠ACB=_____°时，四边形AECF是正方形．
三、解答题
16．已知：如图，平行四边形 ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．
（1）求证：△AOD ≌ △EOC；
（2）连接AC，DE，当∠B∠AEB _______ °时，四边形ACED是正方形？请说明理由．
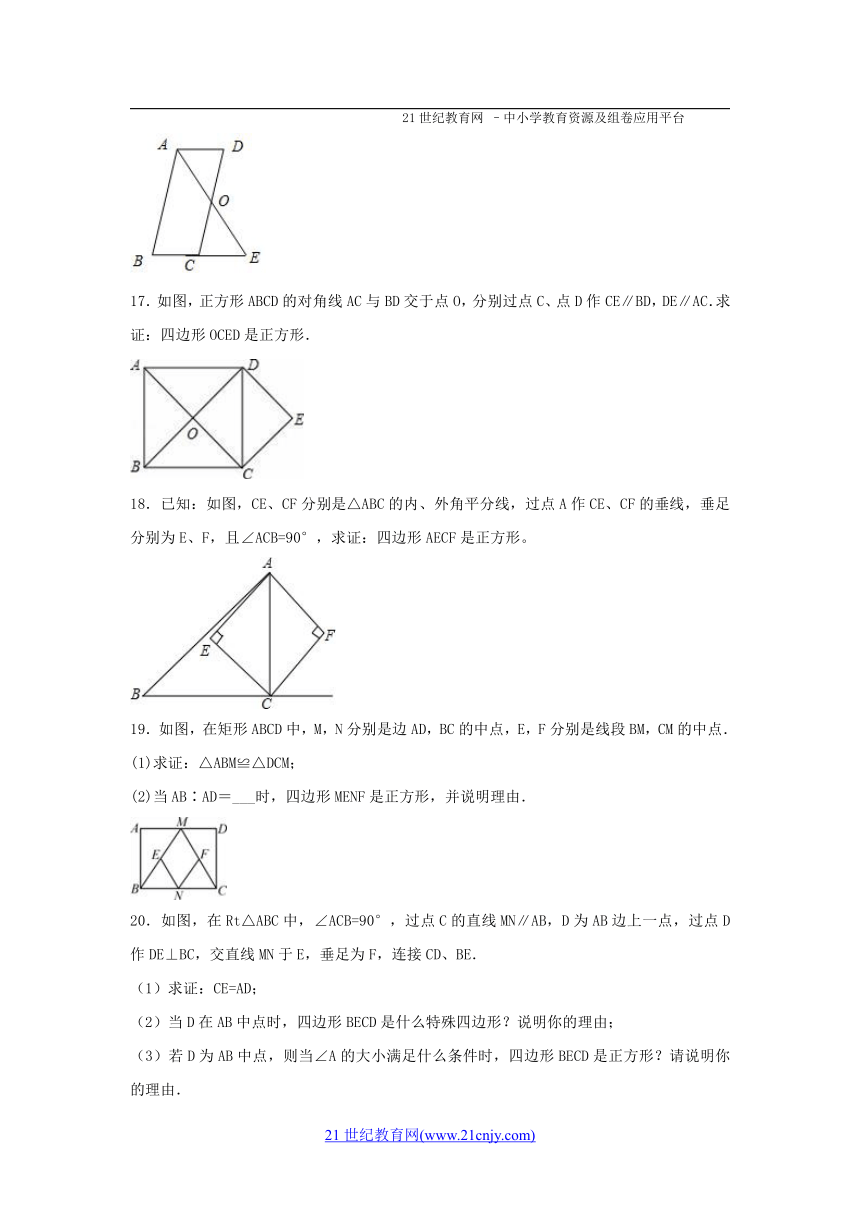
17．如图，正方形ABCD的对角线AC与BD交于点O，分别过点C、点D作CE∥BD，DE∥AC．求证：四边形OCED是正方形．
18．已知：如图，CE、CF分别是△ABC的内、外角平分线，过点A作CE、CF的垂线，垂足分别为E、F，且∠ACB=90°，求证：四边形AECF是正方形。
19．如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
(1)求证：△ABM≌△DCM；
(2)当AB∶AD＝___时，四边形MENF是正方形，并说明理由．
20．如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）求证：CE=AD；
（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．
21．如图，已知正方形ABCD，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．
（1）求证：四边形PMAN是正方形；
（2）求证：EM=BN．
参考答案
1．B
【解析】试题分析：A、有一组对边平行且相等的四边形是平行四边形，故错误；B、正确；C、有一个角是直角的平行四边形是矩形，故错误；D、对角线互相垂直平分且相等的四边形是正方形，故错误；则本题选B．
2．A
【解析】解：A．两条对角线互相平分的四边形是平行四边形，故本选项正确．
B．对角线互相垂直平分的四边形是菱形；故本选项错误．
C．两条对角线互相垂直相等且平分的四边形是正方形．故本选项错误．
D．两条对角线相等且平分的四边形是矩形；故本选项错误．
故选A．
点睛：本题考查了真命题的概念以及平行四边形，菱形，矩形，正方形的判定定理，熟记这些判定定理才能正确的判断正误．
3．C
【解析】A选项四边形ABCD是平行四边形,①AB=BC时,平行四边形ABCD是菱形,
②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意,
B,∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意,
C,∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意,
D,∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.故选C．
4．B
【解析】解：A．根据有一组邻边相等的平行四边形是菱形，或者对角线互相垂直的平行四边形是菱形，所以不能判断平行四边形ABCD是正方形；
B．根据对角线互相垂直的平行四边形是菱形，对角线相等的平行四边形为矩形，所以能判断四边形ABCD是正方形；
C．根据一组邻角相等的平行四边形是矩形，对角线相等的平行四边形也是矩形，即只能证明四边形ABCD是矩形，不能判断四边形ABCD是正方形；
D．根据对角线互相垂直的平行四边形是菱形，对角线互相平分的四边形是平行四边形，所以不能判断四边形ABCD是正方形．
故选B．
5．C
【解析】如图所示，∵四边形ABCD是矩形，
∴∠ABC=∠BCD=∠CDA=∠BAD=90°，
∵AF、BH、CH、DF分别是角平分线，
∴矩形的四个角被分成的八个角都是45°角，
∴∠AEB=180°-45°×2=90°，AE=BE，
同理可得∠F=∠DGC=∠H=90°，
∴四边形EFGH的四个角都是直角，四边形EFGH是矩形，
可以证明△BCH≌△ADF，
∴AF=BH，
∴AF-AE=BH-BE，
即EF=EH，
∴矩形EFGH是正方形，
故选C.
6．D
【解析】AO=BO=CO=DO可得四边形ABCD是矩形，再由AC⊥BD可判定这个四边形是正方形，
故选：D．
【点睛】此题主要考查了正方形的判定，关键是掌握正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；
②先判定四边形是菱形，再判定这个矩形有一个角为直角．③还可以先判定四边形是平行四边形，再用1或2进行判定．
7．D
【解析】分析：本题考查的是正方形的判定方法，平行线的性质与角平分线的性质.
解析：∵MN∥BC，∴∠OEC=∠ECB,∵CE是∠BCA的平分线，∴∠ECB=∠ECA,∴∠ECA=∠OEC，∴OE=OC,同理OC=OF,∵O是AC的中点，∴四边形AECF是平行四边形，∵∠ACB=90°，∴AC=EF,AC⊥EF,∴边形AECF是正方形.
故选D.
8．AB=BC
【解析】本题答案不唯一，
∵四边形ABCD是矩形，
∴（1）当AB=BC时，矩形ABCD是正方形；
（2）当AC⊥BD时，矩形ABCD是正方形.
故答案为：AB=CD（或AC⊥BD）.
点睛：判定一个矩形是正方形的两种主要方法是：（1）有一组邻边相等的矩形是正方形；（2）对角线互相垂直的矩形是正方形.
9．平行四边形 互相垂直 相等 互相垂直且相等
【解析】试题解析：顺次连接四边形各边中点，所得的图形是平行四边形；
(如图)
根据中位线定理可得： 且GF∥BD， 且EH∥BD，
∴EH=FG，EH∥FG，
∴四边形EFGH是平行四边形；
顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形；
如图：
∵E、F. G、H分别为各边中点，
∴EF∥GH∥DB， ，
EH∥FG∥BD，
∵DB⊥AC，
∴EF⊥EH，
∴四边形EFGH是矩形；
顺次连接对角线相等的四边形的各边中点所得的四边形是菱形；
如图，
∵AC=BD，E. F. G、H分别是线段AB、BC、CD、AD的中点
∴EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
根据三角形的中位线的性质，
∴
∵AC=BD，
∴EH=FG=FG=EF，
∴四边形EFGH是菱形；
根据正方形的判别方法知，对角线互相平分，互相垂直且相等的四边形是正方形.
故答案为：平行四边形、互相垂直、相等、互相垂直且相等.
10．AB＝AD(答案不唯一)
【解析】试题解析：添加条件：AB=AD，理由如下：
∵四边形ABCD是矩形，AB=AD，
∴四边形ABCD是正方形，
故答案为：AB=AD(答案不唯一).
11．∠A＝90°，AD＝AF(答案不唯一)
【解析】试题解析：要证明四边形ADEF为正方形，
则要求其四边相等，AB=AC，点D、E、F分别是△ABC的边AB、BC、AC的中点，
则得其为平行四边形，
且有一角为直角，
则在平行四边形的基础上得到正方形．
故答案为：△ABC为等腰直角三角形，且AB=AC，∠A=90°（此题答案不唯一）．
12．AC=BC
【解析】试题解析：∵EF垂直平分BC，
∴BE=EC，BF=CF，
∵BF=BE，
∴BE=EC=CF=BF，
∴四边形BECF是菱形；
当AC=BC时，
∵∠ACB=90°，
则∠A=45°时，菱形BECF是正方形．
13．∠ABC＝90°或AC＝BD
【解析】试题解析：要使菱形成为正方形，只要菱形满足以下条件之一即可，（1）有一个内角是直角（2）对角线相等．
即∠ABC=90°或AC=BD．
故答案为：∠BAD=90°或AC=BD．
14．互相垂直平分且相等
【解析】对角线互相平分的四边形是平行四边形，对角线相等的平行四边形是矩形，对角线互相垂直的矩形是正方形，所以对角线互相垂直平分且相等的四边形是正方形，
故答案为：互相垂直平分且相等.
15．90
【解析】（1）∵MN∥BC，
∴∠OEC=∠ECB，∠OFC=∠FCD．
又∵CE平分∠ACB，FC平分∠ACD．
∴∠ECB=∠OCE，∠OCF=∠FCD，
∴∠OEC=∠OCE，∠OFC=∠OCF，
∴EO=OC，FO=OC，
∴EO=FO；
OE=OC=OF，
当OC=OA，即点O为AC的中点时，
∴OE=OC=OF=OA，
∴四边形AECF是平行四边形，AC=EF，
∴这时四边形AECF是矩形,
∴当点O运动到AC中点时，
四边形AECF是矩形，
由正方形AECF可知，AC⊥EF，
又∵EF∥BC，
∴∠ACB=90°，
∴△ABC是∠ACB=90°.
16．（1）证明见解析（2）当∠B=∠AEB=45°时，四边形ACED是正方形
【解析】试题分析：（1）根据平行线的性质可得∠D=∠OCE，∠DAO=∠E，再根据中点定义可得DO=CO，然后可利用AAS证明△AOD≌△EOC；
（2）当∠B=∠AEB=45°时，四边形ACED是正方形，首先证明四边形ACED是平行四边形，再证对角线互相垂直且相等可得四边形ACED是正方形．
试题解析：证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D=∠OCE，∠DAO=∠E．∵O是CD的中点，∴OC=OD．在△ADO和△ECO中，，∴△AOD≌△EOC（AAS）；
（2）当∠B=∠AEB=45°时，四边形ACED是正方形．
∵△AOD≌△EOC，∴OA=OE．
又∵OC=OD，∴四边形ACED是平行四边形．
∵∠B=∠AEB=45°，∴AB=AE，∠BAE=90°．
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∴∠COE=∠BAE=90°，∴ ACED是菱形．∵AB=AE，AB=CD，∴AE=CD，∴菱形ACED是正方形．
故答案为：45．
点睛：本题主要考查了全等三角形的判定与性质，以及正方形的判定，关键是掌握对角线互相垂直且相等的平行四边形是正方形．
17．证明见解析
【解析】整体分析：
先证明四边形OCED是平行四边形，再由四边形ABCD的性质得到OA=OC=OB=OD，AC⊥BD，即可证明四边形OCED是正方形．
证明：∵CE∥BD，DE∥AC，
∴四边形OCED是平行四边形，
∵四边形ABCD是正方形，
∴OA=OC=OB=OD，AC⊥BD，
∴四边形OCED是正方形．
18．见解析
【解析】试题分析：先证明四边形是矩形，再由，证出即可．
试题解析：证明：∵CE、CF分别是△ABC的内外角平分线，
∵AE⊥CE，AF⊥CF，
∴四边形AECF是矩形，
∴AE=CE，
∴四边形AECF是正方形.
点睛：正方形的判定：有一组邻边相等的矩形是正方形.
19．（1）证明见解析；（2）见解析
【解析】试题分析：（1）利用矩形的性质，利用HL证明△ABM≌△DCM.（2）利用四边形MENF是正方形的结论反推出条件AB∶AD＝1∶2,再用条件证明，先证明∠AMB＝45°.利用△ABM≌△DCM，证明四边形MENF是菱形，最后得菱形MENF是正方形．
试题解析：
解：(1)证明：∵四边形ABCD是矩形，∴AB＝DC，∠A＝∠D＝90°.∵M为AD的中点，∴AM＝MD，∴△ABM≌△DCM.
(2) 1∶2，理由：∵AB∶AD＝1∶2，∴AB＝AD.∵AM＝AD，∴AB＝AM，∴∠ABM＝∠AMB.∵∠A＝90°，∴∠AMB＝45°.∵△ABM≌△DCM，∴BM＝CM，∠DMC＝∠AMB＝45°，∴∠BMC＝90°.∵E，F，N分别是BM，CM，BC的中点，∴EN∥CM，FN∥BM，EM＝MF，
∴四边形MENF是菱形．
∵∠BMC＝90°，
∴菱形MENF是正方形．
20．(1)见解析; (2)见解析; (3)见解析;
【解析】分析：（1）由BC⊥AC，DE⊥BC，得到DE∥AC，从而判断出四边形ADEC是平行四边形．即可，
（2）先判断出△BFD≌△CFE，再判断出BC和DE垂直且互相平分，得到四边形BECD是菱形．
（3）先判断出∠CDB=90°，从而得到有一个角是直角的菱形是正方形．
解析：（1）证明：∵直线m∥AB，
∴EC∥AD．
又∵∠ACB=90°，
∴BC⊥AC．
又∵DE⊥BC，
∴DE∥AC．
∵EC∥AD，DE∥AC，
∴四边形ADEC是平行四边形．
∴CE=AD．
（2）当点D是AB中点时，四边形BECD是菱形．
证明：∵ D是AB中点，
∴DB=DA
又∵直线m∥AB，CE=AD
∴DB= CE，DB ∥ CE
∴四边形BDCE是平行四边形
又∵DE⊥BC
∴四边形BECD是菱形
（3）当∠A的大小是45°时，四边形BECD是正方形．
21．（1）证明见解析；（2）证明见解析.
【解析】试题分析：
（1）先证四边形PMAN是矩形，再证PM=PN；
（2）用ASA证明△EPM≌△BPN.
试题解析：
（1）证明：∵四边形ABCD是正方形，∴∠BAD=90°，AC平分∠BAD，
∵PM⊥AD，PN⊥AB，∴PM=PN，∠PMA=∠PNA=90°，
∴四边形PMAN是矩形，
∵PM=PN，∴四边形PMAN是正方形；
（2）证明：∵四边形PMAN是正方形，∴PM=PN，∠MPN=90°，
∵∠EPB=90°，∴∠MPE+∠EPN=∠NPB+∠EPN=90°，∴∠MPE=∠NPB，
在△EPM和△BPN中，
，
∴△EPM≌△BPN（ASA），
∴EM=BN．
21世纪教育网(www.21cnjy.com)