第5章 特殊平行四边形单元检测提高卷(含解析)
文档属性
| 名称 | 第5章 特殊平行四边形单元检测提高卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 636.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-29 22:28:47 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第5章 特殊平行四边形单元检测提高卷
姓名:__________班级:__________考号:__________
一、选择题(本大题共12小题)
如图是一张矩形纸片, ,若将纸片沿折叠,使落在上,点的对应点为点,若,则( )21cnjy.com
A. B. C. D.
( http: / / www.21cnjy.com / )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF= ( http: / / www.21cnjy.com / ),BD=2,则菱形ABCD的面积为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.2 ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C.6 ( http: / / www.21cnjy.com / ) D.8 ( http: / / www.21cnjy.com / )
如图,把正方形纸片ABCD沿对边中点所 ( http: / / www.21cnjy.com )在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
( http: / / www.21cnjy.com / )
A.2 B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D.1
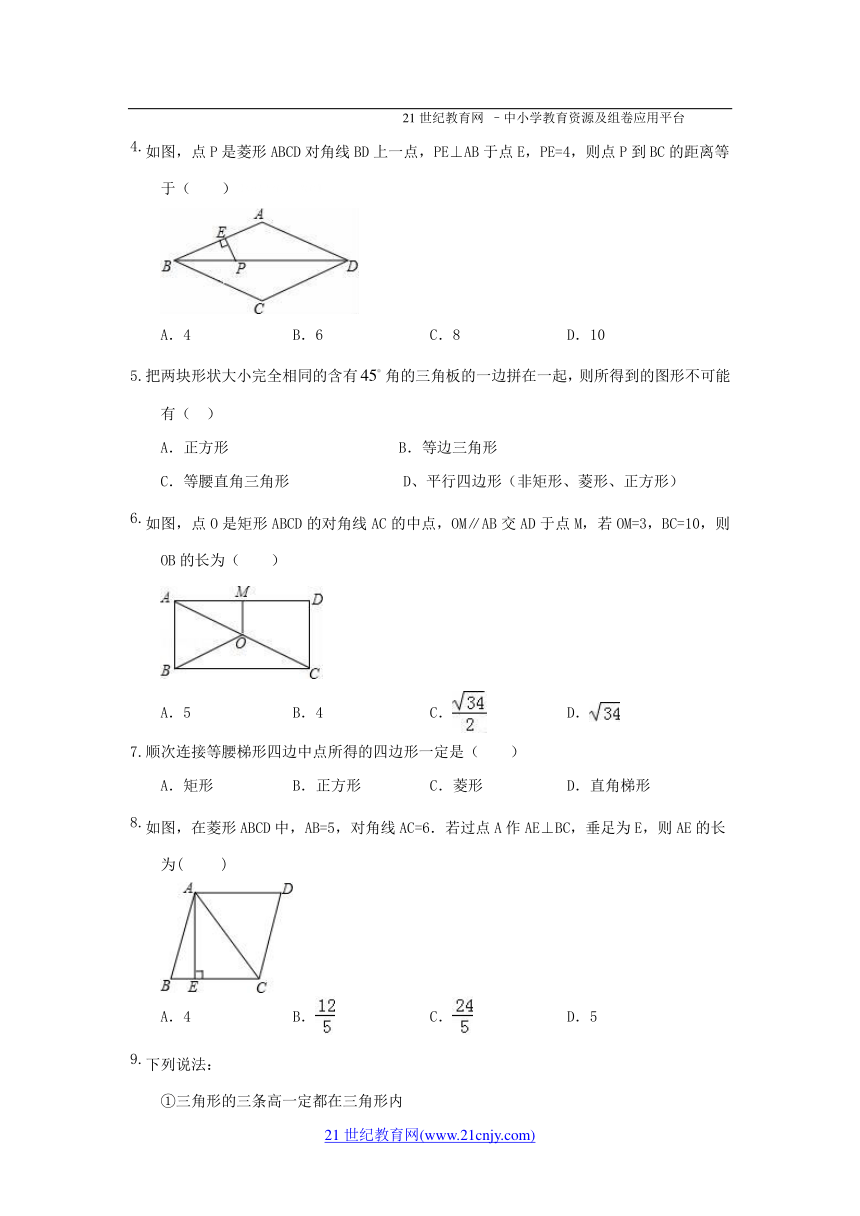
如图,点P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4,则点P到BC的距离等于( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.10
把两块形状大小完全相同的含有角的三角板的一边拼在一起,则所得到的图形不可能有( )
A.正方形 B.等边三角形
C.等腰直角三角形 D、平行四边形(非矩形、菱形、正方形)
如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
( http: / / www.21cnjy.com / )
A.5 B.4 C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
顺次连接等腰梯形四边中点所得的四边形一定是( )
A.矩形 B.正方形 C.菱形 D.直角梯形
如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
( http: / / www.21cnjy.com / )
A.4 B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D.5
下列说法:
①三角形的三条高一定都在三角形内
②有一个角是直角的四边形是矩形
③有一组邻边相等的平行四边形是菱形
④两边及一角对应相等的两个三角形全等
⑤一组对边平行,另一组对边相等的四边形是平行四边形
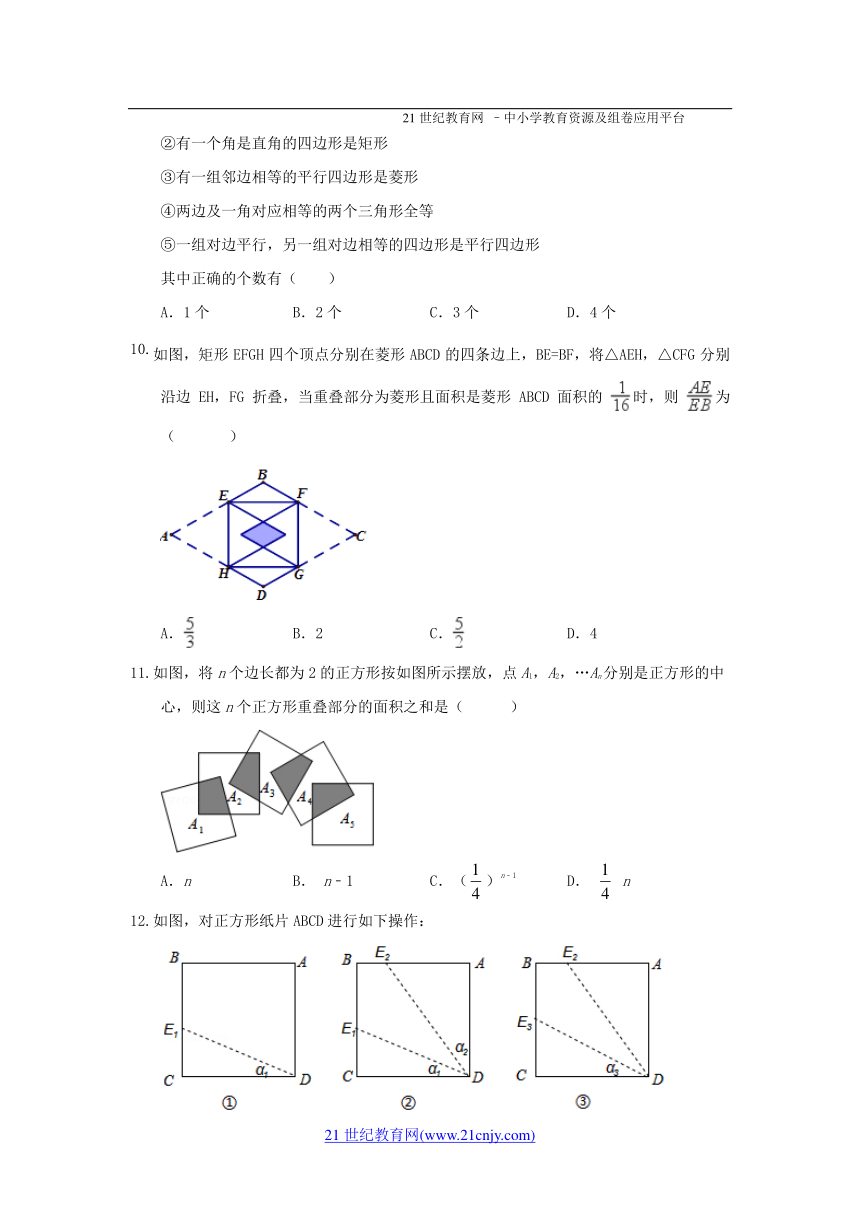
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 ( http: / / www.21cnjy.com / )时,则 ( http: / / www.21cnjy.com / )为( )
( http: / / www.21cnjy.com / )
A. ( http: / / www.21cnjy.com / ) B.2 C. ( http: / / www.21cnjy.com / ) D.4
如图,将n个边长都为2的正方形按如图所示 ( http: / / www.21cnjy.com )摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
( http: / / www.21cnjy.com / )
A.n B. n﹣1 C.()n﹣1 D. n
如图,对正方形纸片ABCD进行如下操作:
( http: / / www.21cnjy.com / )
(1)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=a1;
(2)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=a2;
(3)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=a3;
按此作法从操作(2)起重复以上步骤,得到a1,a2,…,an,…,现有如下结论:
①当a1=10°时,a2=40°;
②2a4+a3=90°;
③当a5=30°时,△CDE9≌△ADE10;
④当a1=45°时,BE2= ( http: / / www.21cnjy.com / )AE2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题)
菱形的一个内角为120°,平分这个内角的对角线长为11厘米,菱形的周长为 .
如图,菱形ABCD中,AC交BD于O,OE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= .21·cn·jy·com
( http: / / www.21cnjy.com / )
如图,矩形ABCD中,对角线AC= ( http: / / www.21cnjy.com / ),E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B’处,则AB= ;
( http: / / www.21cnjy.com / )
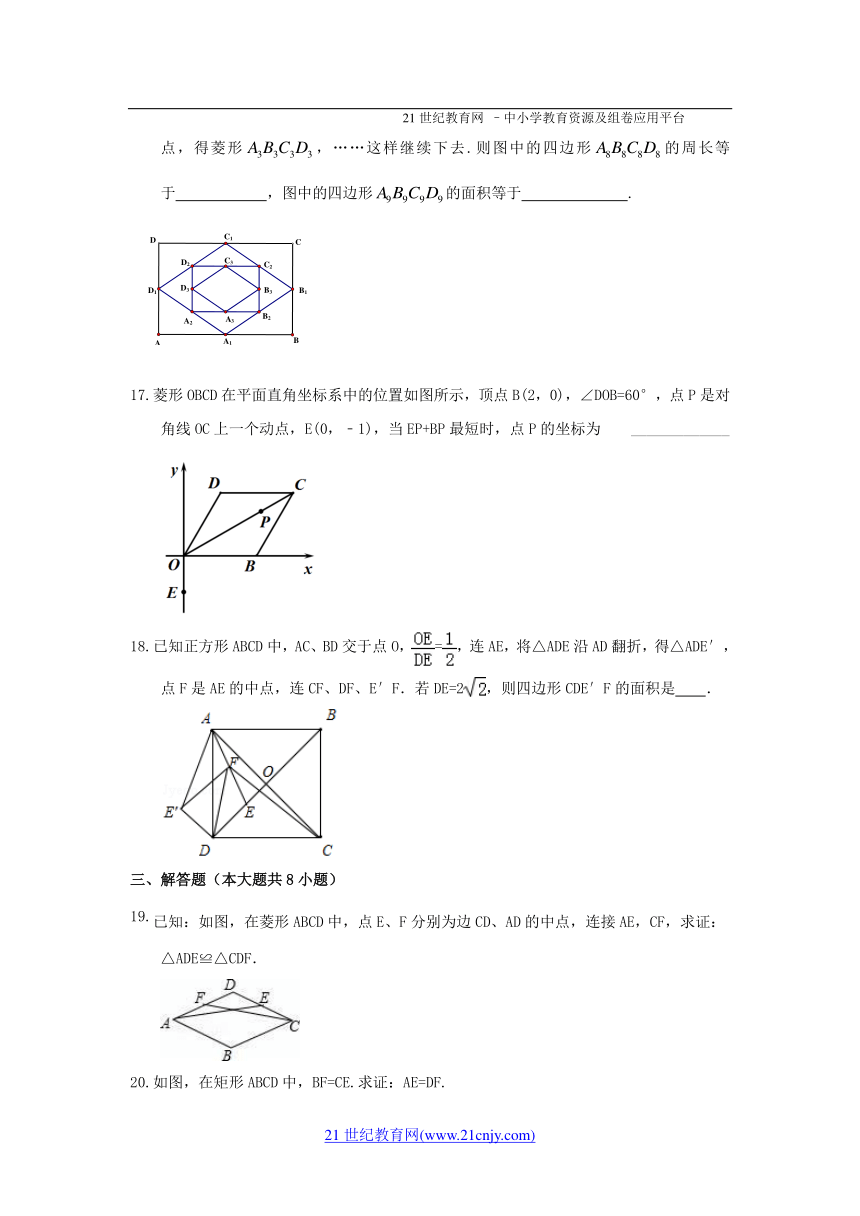
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形;再顺次连结菱形的各边中点,得矩形;再顺次连结矩形的各边中点,得菱形,……这样继续下去.则图中的四边形的周长等于 ,图中的四边形的面积等于 .
菱形OBCD在平面直角坐标系中的位置如图 ( http: / / www.21cnjy.com )所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为 _____________
( http: / / www.21cnjy.com / )
已知正方形ABCD中,AC、BD交于点O, ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),连AE,将△ADE沿AD翻折,得△ADE′,点F是AE的中点,连CF、DF、E′F.若DE=2 ( http: / / www.21cnjy.com / ),则四边形CDE′F的面积是 .
( http: / / www.21cnjy.com / )
三、解答题(本大题共8小题)
已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.
( http: / / www.21cnjy.com / )
如图,在矩形ABCD中,BF=CE.求证:AE=DF.
( http: / / www.21cnjy.com / )
在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
( http: / / www.21cnjy.com / )
如图,正方形ABCD中,点E,F分别在AB,BC上,AF=DE,AF和DE相交于点G.
(1)观察图形,写出图中所有与∠AED相等的角;
(2)选择图中与∠AED相等的任意一个角,并加以证明.
( http: / / www.21cnjy.com / )
如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
( http: / / www.21cnjy.com / )
在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若DE= ( http: / / www.21cnjy.com / )BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
( http: / / www.21cnjy.com / )
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21*cnjy*com
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
( http: / / www.21cnjy.com / )
定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD,
(2)如图2,在矩形ABC ( http: / / www.21cnjy.com )D中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.
( http: / / www.21cnjy.com / )
第5章 特殊平行四边形单元检测提高卷卷答案解析
一 、选择题
A 解析:由折叠知,四边形为正方形,∴ .
【分析】根据中位线定理可得对角线AC的长,再由菱形面积等于对角线乘积的一半可得答案.
解:∵E,F分别是AD,CD边上的中点,EF= ( http: / / www.21cnjy.com / ),
∴AC=2EF=2 ( http: / / www.21cnjy.com / ),
又∵BD=2,
∴菱形ABCD的面积S= ( http: / / www.21cnjy.com / )×AC×BD= ( http: / / www.21cnjy.com / )×2 ( http: / / www.21cnjy.com / )×2=2 ( http: / / www.21cnjy.com / ),
故选:A.
【点评】本题主要考查菱形的性质与中位线定理,熟练掌握中位线定理和菱形面积公式是关键.
【分析】根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值.
解:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM= ( http: / / www.21cnjy.com / ),
故选:B.
【分析】利用菱形的性质,得BD平分∠ABC,利用角平分线的性质,得结果.
解:∵四边形ABCD是菱形,
∴BD平分∠ABC,
∵PE⊥AB,PE=4,
∴点P到BC的距离等于4,
故选A.
【点评】本题主要考查了菱形的性质和角平分线的性质,运用角的平分线上的点到角的两边的距离相等是解答此题的关键.
【考点】正方形、等边三角形、等腰直角三角形、平行四边形(非矩形、菱形、正方形)的定义
【分析】根据常识可知,含有45°角的三 ( http: / / www.21cnjy.com )角板为等腰直角三角形,故可知,当斜边拼在一起可得正方形,将一条直角边拼在一起可得等腰直角三角形和平行四边形,即只有B选项不符题意.2·1·c·n·j·y
解:将两块三角板的斜边拼在一起可得正方形,
将一条直角边拼在一起可得等腰直角三角形和平行四边形.
故选B.
点评:本题主要考查了学生对几何图形的认识和判定,利用学过的知识来探索和发现新的问题.
【考点】矩形的性质.
【分析】已知OM是△ADC的中位线 ( http: / / www.21cnjy.com ),再结合已知条件则DC的长可求出,所以利用勾股定理可求出AC的长,由直角三角形斜边上中线的性质则BO的长即可求出.
解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∴OM=3,
∴DC=6,
∵AD=BC=10,
∴AC= ( http: / / www.21cnjy.com / )=2 ( http: / / www.21cnjy.com / ),
∴BO= ( http: / / www.21cnjy.com / )AC= ( http: / / www.21cnjy.com / ),
故选D.
【考点】中点四边形
【分析】根据等腰梯形的性质及中位线定理和菱形的判定,可推出四边形为菱形
解:如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点,
求证:四边形EFGH是菱形.
证明:连接AC、BD.
∵E、F分别是AB、BC的中点,
∴EF=AC.
同理FG=BD,GH=AC,EH=BD,
又∵四边形ABCD是等腰梯形,
∴AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
故选C.
( http: / / www.21cnjy.com / )
【考点】菱形的性质.
【分析】连接BD,根据菱形的性质可得AC⊥BD,AO= ( http: / / www.21cnjy.com / )AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC AE= ( http: / / www.21cnjy.com / )AC BD可得答案.
解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO= ( http: / / www.21cnjy.com / )AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0= ( http: / / www.21cnjy.com / )=4,
∴DB=8,
∴菱形ABCD的面积是 ( http: / / www.21cnjy.com / )×AC DB= ( http: / / www.21cnjy.com / )×6×8=24,
∴BC AE=24,
AE= ( http: / / www.21cnjy.com / ),
故选:C.
( http: / / www.21cnjy.com / )
【点评】此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.
解:①错误,理由:钝角三角形有两条高在三角形外.
②错误,理由:有一个角是直角的四边形是矩形不一定是矩形,有三个角是直角的四边形是矩形.
③正确,有一组邻边相等的平行四边形是菱形.
④错误,理由两边及一角对应相等的两个三角形不一定全等.
⑤错误,理由:一组对边平行,另一组对边相等的四边形不一定是平行四边形有可能是等腰梯形.
正确的只有③,
故选A.
【考点】菱形的性质,翻折变换(折叠问题)
【分析】依题可得阴影部分是菱形.设 ( http: / / www.21cnjy.com )S菱形ABCD=16,BE=x.从而得出AB=4,阴影部分边长为4-2x.根据(4-2x)2=1求出x,从而得出答案. 【来源:21·世纪·教育·网】
解:依题可得阴影部分是菱形.
∴设S菱形ABCD=16,BE=x.
∴AB=4.
∴阴影部分边长为4-2x.
∴(4-2x)2=1.
∴4-2x=1或4-2x=-1.
∴x= ( http: / / www.21cnjy.com / )或x= ( http: / / www.21cnjy.com / )(舍去).
∴ ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ).
故答案为A.
【考点】正方形的性质;全等三角形的判定与性质
【分析】根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n﹣1)个阴影部分的和.
解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,
5个这样的正方形重叠部分(阴影部分)的面积和为:1×4,
n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.
故选:B.
点评: 此题考查了正方形的性质,解决本 ( http: / / www.21cnjy.com )题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
【分析】①根据角平分线的定义计算即可;
②根据题意、结合图形计算;
③根据全等三角形的判定定理证明;
④作E2F⊥BD于F,根据等腰直角三角形的性质得到BE2= ( http: / / www.21cnjy.com / )FE2,根据角平分线的性质得到AE2=FE2,等量代换即可.21世纪教育网版权所有
解:①当a1=10°时,a2= ( http: / / www.21cnjy.com / )=40°,①正确;
②由图③可知,2a4+a3=90°,②正确;
③当a5=30°时,a9=30°,a10=30°,
在△CDE9和△ADE10中,
( http: / / www.21cnjy.com / ),
∴△CDE9≌△ADE10,③正确;
④当a1=45°时,点E1与点B重合,
作E2F⊥BD于F,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴BE2= ( http: / / www.21cnjy.com / )FE2,
∵DE2平分∠ADB,E2F⊥BD,∠A=90°,
∴AE2=FE2,
∴BE2= ( http: / / www.21cnjy.com / )AE2,④正确,
故选:D.
( http: / / www.21cnjy.com / )
【点评】本题考查的是正方形 ( http: / / www.21cnjy.com )的性质、角平分线的性质、全等三角形的判定,掌握角平分线上的点到角的两边的距离相等、全等三角形的判定定理是解题的关键.
二 、填空题
【考点】 菱形的性质.
【分析】 首先根据题意画出图形,然后由菱形的一个内角为120°,可得△ABC是等边三角形,继而求得边长,则可求得答案.21教育网
解:如图,∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,AC平分∠BAD,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=11厘米,
∴菱形的周长为:44厘米.
故答案为:44厘米.
( http: / / www.21cnjy.com / )
点评: 此题考查了菱形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
【分析】由菱形的性质可 ( http: / / www.21cnjy.com )知O为BD中点,所以OE为直角三角形BED斜边上的中线,由此可得OE=OB,根据等腰三角形的性质和已知条件即可求出∠OED的度数.
解:
∵四边形ABCD是菱形,
∴DO=OB,
∵DE⊥BC于E,
∴OE为直角三角形BED斜边上的中线,
∴OE= ( http: / / www.21cnjy.com / )BD,
∴OB=OE,
∴∠OBE=∠OEB,
∵∠ABC=140°,
∴∠OBE=70°,
∴∠OED=90°﹣70°=20°,
故答案为:20°.
【点评】本题考查了菱形的性质、直角三角形斜边上中线的性质,得到OE为直角三角形BED斜边上的中线是解题的关键.www-2-1-cnjy-com
解:由折叠知,三角形ABE与三角形A ( http: / / www.21cnjy.com / )E全等,所以,AB=A ( http: / / www.21cnjy.com / ),BE= ( http: / / www.21cnjy.com / )E,
∠A ( http: / / www.21cnjy.com / )E=∠ABE=90°
又BC=3BE,有EC=2BE,所以,EC=2 ( http: / / www.21cnjy.com / )E,所以,∠ACE=30°,∠BAC=60°,
又由折叠知:∠ ( http: / / www.21cnjy.com / )AE=∠BAE=30°,所以,∠EAC=∠ECA=30°,
所以,EA=EC,又∠A ( http: / / www.21cnjy.com / )E=90°,由等腰三角形性质,知 ( http: / / www.21cnjy.com / )为AC中点,
所以,AB=A ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )
解:在矩形ABCD中,AB=16,BC=12,根据题意可得:菱形 ( http: / / www.21cnjy.com / )的两条对角线的长分别等于矩形ABCD的两边长16,12,所以菱形 ( http: / / www.21cnjy.com / )的面积= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )矩形ABCD的面积;矩形 ( http: / / www.21cnjy.com / )的两边长分别等于矩形ABCD的两边长的 ( http: / / www.21cnjy.com / ),所以矩形 ( http: / / www.21cnjy.com / )的周长=矩形ABCD的周长的 ( http: / / www.21cnjy.com / )=28,,以此类推可得菱形 ( http: / / www.21cnjy.com / )的面积=矩形 ( http: / / www.21cnjy.com / )的面积的 ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),矩形 ( http: / / www.21cnjy.com / )的的周长=矩形 ( http: / / www.21cnjy.com / )的周长的 ( http: / / www.21cnjy.com / )=矩形ABCD的周长的 ( http: / / www.21cnjy.com / )=14,.....
所以四边形 ( http: / / www.21cnjy.com / )的周长= ( http: / / www.21cnjy.com / ),四边形 ( http: / / www.21cnjy.com / )的面积= ( http: / / www.21cnjy.com / ).
【考点】菱形的性质;坐标与图形性质;轴对称-最短路线问题
【分析】点B的对称点是点D,连接ED,交OC于点P,再得出ED即为EP+BP最短,解答即可
解:如图,连接DE交OC于点P,即点P满足EP+BP最短.
( http: / / www.21cnjy.com / )
如图,延长CD交y轴于点F,则CF⊥y轴,
∵四边形OBCD是菱形,
∵OD=CD=OB=2,
∵∠DOB=60°,则∠DOF=30°,
∴DF=1,OF= ( http: / / www.21cnjy.com / ),
∴D(1, ( http: / / www.21cnjy.com / )),C(3, ( http: / / www.21cnjy.com / )),
设直线DE的解析式为 ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
∴ ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
设直线OC的解析为 ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
∴ ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
由 ( http: / / www.21cnjy.com / ),得 ( http: / / www.21cnjy.com / ),
∴点P的坐标为 ( http: / / www.21cnjy.com / ).
【考点】翻折变换(折叠问题);三角形的角平分线、中线和高;等腰直角三角形;正方形的性质.
【分析】先连接EC、EE′,设EE′交 ( http: / / www.21cnjy.com )AD于N,根据正方形的性质以及折叠的性质,求出NE、ND的长,以及正方形ABCD的对角线长和边长,再根据CF是△ACE的中线,求出△ACF的面积,根据E′F是△AE′E的中线,求出△AE′F的面积,最后根据四边形CDE′F的面积=S梯形ACDE′﹣S△ACF﹣S△AE′F进行计算,即可解决问题.
解:连接EE′,交AD于N,连接CE,
在正方形ABCD中,∠EDN=45°,
由折叠得,AD垂直平分EE′,且∠EDN=∠E′DN=45°,DE=DE′,
∴△DEE′、△DEN、△DE′N均为等腰直角三角形,
∵DE=2 ( http: / / www.21cnjy.com / ), ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),
∴OE= ( http: / / www.21cnjy.com / ),DN=EN=E′N=2,DO=3 ( http: / / www.21cnjy.com / ),DE′=2 ( http: / / www.21cnjy.com / ),
∴AC=6 ( http: / / www.21cnjy.com / ),AD=6,
∵EO⊥AC,
∴S△ACE= ( http: / / www.21cnjy.com / )×6 ( http: / / www.21cnjy.com / )× ( http: / / www.21cnjy.com / )=6,
又∵点F是AE的中点,
∴S△ACF= ( http: / / www.21cnjy.com / )×S△ACE=3,
∵AN⊥EE′,AN=AD﹣DN=6﹣2=4,
∴S△AE′E= ( http: / / www.21cnjy.com / )×4×4=8,
又∵点F是AE的中点,
∴S△AE′F= ( http: / / www.21cnjy.com / )×S△AE′E=4,
∵∠E′DO=∠AOD=90°,
∴DE′∥AC,
∴S梯形ACDE′= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )=24,
∴四边形CDE′F的面积=S梯形ACDE′﹣S△ACF﹣S△AE′F=24﹣3﹣4=17.
故答案为:17
( http: / / www.21cnjy.com / )
三 、解答题
【考点】菱形的性质;全等三角形的判定.
【分析】由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由SAS证明△ADE≌△CDF即可.2-1-c-n-j-y
证明:∵四边形ABCD是菱形,
∴AD=CD,
∵点E、F分别为边CD、AD的中点,
∴AD=2DF,CD=2DE,
∴DE=DF,
在△ADE和△CDF中, ( http: / / www.21cnjy.com / ),
∴△ADE≌△CDF(SAS).
【点评】此题主要考查了全等三角形的判定、菱形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.21·世纪*教育网
【考点】全等三角形的判定与性质
【分析】根据矩形的性质得出AB=CD,∠B=∠C=90°,求出BE=CF,根据SAS推出△ABE≌△DCF即可;21*cnjy*com
解: ∵四边形ABCD是矩形.
∴AB=CD ∠ABC=∠DCB
∵BF=CE
∴BC-BF=BC-CE
即BE=FC
∴△ABE≌△DCF(SAS)
∴AE=DF
【考点】菱形的性质;全等三角形的判定与性质;勾股定理
【分析】(1)根据四边形ABCD是菱形 ( http: / / www.21cnjy.com ),判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=6,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少【出处:21教育名师】
解:(1)∵四边形ABCD为菱形,∴AD∥BC,AO=CO. ∴∠MAO=∠NCO.
在△AOM与△CON中, ( http: / / www.21cnjy.com / )∴△AOM≌△CON.∴OM=ON.
(2)依题意,DE∥AC,又AC⊥ ( http: / / www.21cnjy.com )BD,AD∥BC,∴四边形ACED为平行四边形,DE⊥BD.∴CE=AD=AB=BC=6,DE=AC=8.21教育名师原创作品
∴在Rt△BDE中,由勾股定理,得 ( http: / / www.21cnjy.com / ).
∴△BDE的周长为BD+BE+DE= ( http: / / www.21cnjy.com / )+20.
【考点】全等三角形的判定与性质;正方形的性质
【分析】(1)由图示得出∠DAG,∠AFB,∠CDE与∠AED相等;
(2)根据SAS证明△DAE与△ABF全等,利用全等三角形的性质即可证明.
解:(1)与∠AED相等的角有 ( http: / / www.21cnjy.com / ).
(2)选择 ( http: / / www.21cnjy.com / ):
正方形ABCD中, ( http: / / www.21cnjy.com / ),
又∵AF=DE,∴ ( http: / / www.21cnjy.com / ).∴ ( http: / / www.21cnjy.com / ).
或选择∠DAG=∠AED,证明如下:
∵正方形ABCD,
∴∠DAB=∠B=90°,AD=AB,
∵AF=DE,
∴△DAE≌△ABF(SAS),
∴∠ADE=∠BAF,
∵∠DAG+∠BAF=90°,∠GDA+∠AED=90°,
∴∠DAG=∠AED.
【考点】全等三角形的判定与性质;正方形的性质..
【分析】(1)由正方形的性质得出AB=C ( http: / / www.21cnjy.com )B,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,由SAS证明△ABG≌△CBE,得出对应边相等即可;www.21-cn-jy.com
(2)由△ABG≌△CBE,得出对应 ( http: / / www.21cnjy.com )角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
(1)证明:∵四边形ABCD、BEFG均为正方形,
∴AB=CB,∠ABC=∠GBE=90°,BG=BE,
∴∠ABG=∠CBE,
在△ABG和△CBE中, ( http: / / www.21cnjy.com / ),
∴△ABG≌△CBE(SAS),
∴AG=CE;
(2)证明:如图所示:∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠ABC=90°,
∴∠BAG+∠AMB=90°,
∵∠AMB=∠CMN,
∴∠BCE+∠CMN=90°,
∴∠CNM=90°,
∴AG⊥CE.
( http: / / www.21cnjy.com / )
点评:本题考查了正方形的性质、全等三角形的判定与性质、垂线的证法;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.
【考点】矩形的判定;全等三角形的判定与性质.
【分析】(1)根据平行线得出∠CED=∠BFD,根据AAS推出两三角形全等即可;
(2)根据全等得出DE=DF,根据BD=DC推出四边形是平行四边形,求出∠BEC=90°,根据矩形的判定推出即可.
(1)证明:∵CE∥BF,
∴∠CED=∠BFD,
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中
( http: / / www.21cnjy.com / ),
∴△BDF≌△CDE(AAS);
(2)四边形BFCE是矩形,
证明:∵△BDF≌△CDE,
∴DE=DF,
∵BD=DC,
∴四边形BFCE是平行四边形,
∵BD=CD,DE= ( http: / / www.21cnjy.com / )BC,
∴BD=DC=DE,
∴∠BEC=90°,
∴平行四边形BFCE是矩形.
【点评】本题考查了平行线性质,全等三角形的性质和判定,矩形的判定,平行四边形的判定的应用,注意:有一个角是直角的平行四边形是矩形.
【考点】正方形的判定;全等三角形的判定与性质;等腰三角形的性质.
【分析】(1)利用等腰三角形的性质,可得到∠B=∠C,D又是BC的中点,利用AAS,可证出:△BED≌△CFD.
(2)利用(1)的结论可知,DE=DF,再加上三个角都是直角,可证出四边形DFAE是正方形.
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,
∴∠B=∠C.
∵D是BC的中点,
∴BD=CD.
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,
∴四边形DFAE为矩形.
∵△BED≌△CFD,
∴DE=DF.
∴四边形DFAE为正方形.
【点评】本题利用了全等三角形的判定和性 ( http: / / www.21cnjy.com )质以及矩形、正方形的判定.解答此题的关键是利用等腰三角形的两个底角相等,从而证明Rt△BED和Rt△CFD中的两个锐角对应相等.
【考点】四边形综合题.
【分析】(1)①只要证明四边形ABCD是正方形即可解决问题;
②只要证明△ABD≌△CBD,即可解决问题;
(2)若EF⊥BC,则AE≠E ( http: / / www.21cnjy.com )F,BF≠EF,推出四边形ABFE表示等腰直角四边形,不符合条件.若EF与BC不垂直,①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,分别求解即可;
解:(1)①∵AB=AC=1,AB∥CD,
∴S四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形,
∵∠ABC=90°,
∴四边形ABCD是正方形,
∴BD=AC= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ).
(2)如图1中,连接AC、BD.
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD,
∵BD=BD,
∴△ABD≌△CBD,
∴AD=CD.
(2)若EF⊥BC,则AE≠EF,BF≠EF,
∴四边形ABFE表示等腰直角四边形,不符合条件.
若EF与BC不垂直,
①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,
∴AE=AB=5.
②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,
∴BF=AB=5,
∵DE∥BF,
∴DE:BF=PD:PB=1:2,
∴DE=2.5,
∴AE=9﹣2.5=6.5,
综上所述,满足条件的AE的长为5或6.5.
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
21世纪教育网(www.21cnjy.com)
第5章 特殊平行四边形单元检测提高卷
姓名:__________班级:__________考号:__________
一、选择题(本大题共12小题)
如图是一张矩形纸片, ,若将纸片沿折叠,使落在上,点的对应点为点,若,则( )21cnjy.com
A. B. C. D.
( http: / / www.21cnjy.com / )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF= ( http: / / www.21cnjy.com / ),BD=2,则菱形ABCD的面积为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.2 ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C.6 ( http: / / www.21cnjy.com / ) D.8 ( http: / / www.21cnjy.com / )
如图,把正方形纸片ABCD沿对边中点所 ( http: / / www.21cnjy.com )在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
( http: / / www.21cnjy.com / )
A.2 B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D.1
如图,点P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4,则点P到BC的距离等于( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.10
把两块形状大小完全相同的含有角的三角板的一边拼在一起,则所得到的图形不可能有( )
A.正方形 B.等边三角形
C.等腰直角三角形 D、平行四边形(非矩形、菱形、正方形)
如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
( http: / / www.21cnjy.com / )
A.5 B.4 C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
顺次连接等腰梯形四边中点所得的四边形一定是( )
A.矩形 B.正方形 C.菱形 D.直角梯形
如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
( http: / / www.21cnjy.com / )
A.4 B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D.5
下列说法:
①三角形的三条高一定都在三角形内
②有一个角是直角的四边形是矩形
③有一组邻边相等的平行四边形是菱形
④两边及一角对应相等的两个三角形全等
⑤一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 ( http: / / www.21cnjy.com / )时,则 ( http: / / www.21cnjy.com / )为( )
( http: / / www.21cnjy.com / )
A. ( http: / / www.21cnjy.com / ) B.2 C. ( http: / / www.21cnjy.com / ) D.4
如图,将n个边长都为2的正方形按如图所示 ( http: / / www.21cnjy.com )摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
( http: / / www.21cnjy.com / )
A.n B. n﹣1 C.()n﹣1 D. n
如图,对正方形纸片ABCD进行如下操作:
( http: / / www.21cnjy.com / )
(1)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=a1;
(2)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=a2;
(3)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=a3;
按此作法从操作(2)起重复以上步骤,得到a1,a2,…,an,…,现有如下结论:
①当a1=10°时,a2=40°;
②2a4+a3=90°;
③当a5=30°时,△CDE9≌△ADE10;
④当a1=45°时,BE2= ( http: / / www.21cnjy.com / )AE2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题)
菱形的一个内角为120°,平分这个内角的对角线长为11厘米,菱形的周长为 .
如图,菱形ABCD中,AC交BD于O,OE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= .21·cn·jy·com
( http: / / www.21cnjy.com / )
如图,矩形ABCD中,对角线AC= ( http: / / www.21cnjy.com / ),E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B’处,则AB= ;
( http: / / www.21cnjy.com / )
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形;再顺次连结菱形的各边中点,得矩形;再顺次连结矩形的各边中点,得菱形,……这样继续下去.则图中的四边形的周长等于 ,图中的四边形的面积等于 .
菱形OBCD在平面直角坐标系中的位置如图 ( http: / / www.21cnjy.com )所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为 _____________
( http: / / www.21cnjy.com / )
已知正方形ABCD中,AC、BD交于点O, ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),连AE,将△ADE沿AD翻折,得△ADE′,点F是AE的中点,连CF、DF、E′F.若DE=2 ( http: / / www.21cnjy.com / ),则四边形CDE′F的面积是 .
( http: / / www.21cnjy.com / )
三、解答题(本大题共8小题)
已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.
( http: / / www.21cnjy.com / )
如图,在矩形ABCD中,BF=CE.求证:AE=DF.
( http: / / www.21cnjy.com / )
在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
( http: / / www.21cnjy.com / )
如图,正方形ABCD中,点E,F分别在AB,BC上,AF=DE,AF和DE相交于点G.
(1)观察图形,写出图中所有与∠AED相等的角;
(2)选择图中与∠AED相等的任意一个角,并加以证明.
( http: / / www.21cnjy.com / )
如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
( http: / / www.21cnjy.com / )
在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若DE= ( http: / / www.21cnjy.com / )BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
( http: / / www.21cnjy.com / )
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21*cnjy*com
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
( http: / / www.21cnjy.com / )
定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD,
(2)如图2,在矩形ABC ( http: / / www.21cnjy.com )D中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.
( http: / / www.21cnjy.com / )
第5章 特殊平行四边形单元检测提高卷卷答案解析
一 、选择题
A 解析:由折叠知,四边形为正方形,∴ .
【分析】根据中位线定理可得对角线AC的长,再由菱形面积等于对角线乘积的一半可得答案.
解:∵E,F分别是AD,CD边上的中点,EF= ( http: / / www.21cnjy.com / ),
∴AC=2EF=2 ( http: / / www.21cnjy.com / ),
又∵BD=2,
∴菱形ABCD的面积S= ( http: / / www.21cnjy.com / )×AC×BD= ( http: / / www.21cnjy.com / )×2 ( http: / / www.21cnjy.com / )×2=2 ( http: / / www.21cnjy.com / ),
故选:A.
【点评】本题主要考查菱形的性质与中位线定理,熟练掌握中位线定理和菱形面积公式是关键.
【分析】根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值.
解:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM= ( http: / / www.21cnjy.com / ),
故选:B.
【分析】利用菱形的性质,得BD平分∠ABC,利用角平分线的性质,得结果.
解:∵四边形ABCD是菱形,
∴BD平分∠ABC,
∵PE⊥AB,PE=4,
∴点P到BC的距离等于4,
故选A.
【点评】本题主要考查了菱形的性质和角平分线的性质,运用角的平分线上的点到角的两边的距离相等是解答此题的关键.
【考点】正方形、等边三角形、等腰直角三角形、平行四边形(非矩形、菱形、正方形)的定义
【分析】根据常识可知,含有45°角的三 ( http: / / www.21cnjy.com )角板为等腰直角三角形,故可知,当斜边拼在一起可得正方形,将一条直角边拼在一起可得等腰直角三角形和平行四边形,即只有B选项不符题意.2·1·c·n·j·y
解:将两块三角板的斜边拼在一起可得正方形,
将一条直角边拼在一起可得等腰直角三角形和平行四边形.
故选B.
点评:本题主要考查了学生对几何图形的认识和判定,利用学过的知识来探索和发现新的问题.
【考点】矩形的性质.
【分析】已知OM是△ADC的中位线 ( http: / / www.21cnjy.com ),再结合已知条件则DC的长可求出,所以利用勾股定理可求出AC的长,由直角三角形斜边上中线的性质则BO的长即可求出.
解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∴OM=3,
∴DC=6,
∵AD=BC=10,
∴AC= ( http: / / www.21cnjy.com / )=2 ( http: / / www.21cnjy.com / ),
∴BO= ( http: / / www.21cnjy.com / )AC= ( http: / / www.21cnjy.com / ),
故选D.
【考点】中点四边形
【分析】根据等腰梯形的性质及中位线定理和菱形的判定,可推出四边形为菱形
解:如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点,
求证:四边形EFGH是菱形.
证明:连接AC、BD.
∵E、F分别是AB、BC的中点,
∴EF=AC.
同理FG=BD,GH=AC,EH=BD,
又∵四边形ABCD是等腰梯形,
∴AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
故选C.
( http: / / www.21cnjy.com / )
【考点】菱形的性质.
【分析】连接BD,根据菱形的性质可得AC⊥BD,AO= ( http: / / www.21cnjy.com / )AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC AE= ( http: / / www.21cnjy.com / )AC BD可得答案.
解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO= ( http: / / www.21cnjy.com / )AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0= ( http: / / www.21cnjy.com / )=4,
∴DB=8,
∴菱形ABCD的面积是 ( http: / / www.21cnjy.com / )×AC DB= ( http: / / www.21cnjy.com / )×6×8=24,
∴BC AE=24,
AE= ( http: / / www.21cnjy.com / ),
故选:C.
( http: / / www.21cnjy.com / )
【点评】此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.
解:①错误,理由:钝角三角形有两条高在三角形外.
②错误,理由:有一个角是直角的四边形是矩形不一定是矩形,有三个角是直角的四边形是矩形.
③正确,有一组邻边相等的平行四边形是菱形.
④错误,理由两边及一角对应相等的两个三角形不一定全等.
⑤错误,理由:一组对边平行,另一组对边相等的四边形不一定是平行四边形有可能是等腰梯形.
正确的只有③,
故选A.
【考点】菱形的性质,翻折变换(折叠问题)
【分析】依题可得阴影部分是菱形.设 ( http: / / www.21cnjy.com )S菱形ABCD=16,BE=x.从而得出AB=4,阴影部分边长为4-2x.根据(4-2x)2=1求出x,从而得出答案. 【来源:21·世纪·教育·网】
解:依题可得阴影部分是菱形.
∴设S菱形ABCD=16,BE=x.
∴AB=4.
∴阴影部分边长为4-2x.
∴(4-2x)2=1.
∴4-2x=1或4-2x=-1.
∴x= ( http: / / www.21cnjy.com / )或x= ( http: / / www.21cnjy.com / )(舍去).
∴ ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ).
故答案为A.
【考点】正方形的性质;全等三角形的判定与性质
【分析】根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n﹣1)个阴影部分的和.
解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,
5个这样的正方形重叠部分(阴影部分)的面积和为:1×4,
n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.
故选:B.
点评: 此题考查了正方形的性质,解决本 ( http: / / www.21cnjy.com )题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
【分析】①根据角平分线的定义计算即可;
②根据题意、结合图形计算;
③根据全等三角形的判定定理证明;
④作E2F⊥BD于F,根据等腰直角三角形的性质得到BE2= ( http: / / www.21cnjy.com / )FE2,根据角平分线的性质得到AE2=FE2,等量代换即可.21世纪教育网版权所有
解:①当a1=10°时,a2= ( http: / / www.21cnjy.com / )=40°,①正确;
②由图③可知,2a4+a3=90°,②正确;
③当a5=30°时,a9=30°,a10=30°,
在△CDE9和△ADE10中,
( http: / / www.21cnjy.com / ),
∴△CDE9≌△ADE10,③正确;
④当a1=45°时,点E1与点B重合,
作E2F⊥BD于F,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴BE2= ( http: / / www.21cnjy.com / )FE2,
∵DE2平分∠ADB,E2F⊥BD,∠A=90°,
∴AE2=FE2,
∴BE2= ( http: / / www.21cnjy.com / )AE2,④正确,
故选:D.
( http: / / www.21cnjy.com / )
【点评】本题考查的是正方形 ( http: / / www.21cnjy.com )的性质、角平分线的性质、全等三角形的判定,掌握角平分线上的点到角的两边的距离相等、全等三角形的判定定理是解题的关键.
二 、填空题
【考点】 菱形的性质.
【分析】 首先根据题意画出图形,然后由菱形的一个内角为120°,可得△ABC是等边三角形,继而求得边长,则可求得答案.21教育网
解:如图,∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,AC平分∠BAD,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=11厘米,
∴菱形的周长为:44厘米.
故答案为:44厘米.
( http: / / www.21cnjy.com / )
点评: 此题考查了菱形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
【分析】由菱形的性质可 ( http: / / www.21cnjy.com )知O为BD中点,所以OE为直角三角形BED斜边上的中线,由此可得OE=OB,根据等腰三角形的性质和已知条件即可求出∠OED的度数.
解:
∵四边形ABCD是菱形,
∴DO=OB,
∵DE⊥BC于E,
∴OE为直角三角形BED斜边上的中线,
∴OE= ( http: / / www.21cnjy.com / )BD,
∴OB=OE,
∴∠OBE=∠OEB,
∵∠ABC=140°,
∴∠OBE=70°,
∴∠OED=90°﹣70°=20°,
故答案为:20°.
【点评】本题考查了菱形的性质、直角三角形斜边上中线的性质,得到OE为直角三角形BED斜边上的中线是解题的关键.www-2-1-cnjy-com
解:由折叠知,三角形ABE与三角形A ( http: / / www.21cnjy.com / )E全等,所以,AB=A ( http: / / www.21cnjy.com / ),BE= ( http: / / www.21cnjy.com / )E,
∠A ( http: / / www.21cnjy.com / )E=∠ABE=90°
又BC=3BE,有EC=2BE,所以,EC=2 ( http: / / www.21cnjy.com / )E,所以,∠ACE=30°,∠BAC=60°,
又由折叠知:∠ ( http: / / www.21cnjy.com / )AE=∠BAE=30°,所以,∠EAC=∠ECA=30°,
所以,EA=EC,又∠A ( http: / / www.21cnjy.com / )E=90°,由等腰三角形性质,知 ( http: / / www.21cnjy.com / )为AC中点,
所以,AB=A ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )
解:在矩形ABCD中,AB=16,BC=12,根据题意可得:菱形 ( http: / / www.21cnjy.com / )的两条对角线的长分别等于矩形ABCD的两边长16,12,所以菱形 ( http: / / www.21cnjy.com / )的面积= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )矩形ABCD的面积;矩形 ( http: / / www.21cnjy.com / )的两边长分别等于矩形ABCD的两边长的 ( http: / / www.21cnjy.com / ),所以矩形 ( http: / / www.21cnjy.com / )的周长=矩形ABCD的周长的 ( http: / / www.21cnjy.com / )=28,,以此类推可得菱形 ( http: / / www.21cnjy.com / )的面积=矩形 ( http: / / www.21cnjy.com / )的面积的 ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),矩形 ( http: / / www.21cnjy.com / )的的周长=矩形 ( http: / / www.21cnjy.com / )的周长的 ( http: / / www.21cnjy.com / )=矩形ABCD的周长的 ( http: / / www.21cnjy.com / )=14,.....
所以四边形 ( http: / / www.21cnjy.com / )的周长= ( http: / / www.21cnjy.com / ),四边形 ( http: / / www.21cnjy.com / )的面积= ( http: / / www.21cnjy.com / ).
【考点】菱形的性质;坐标与图形性质;轴对称-最短路线问题
【分析】点B的对称点是点D,连接ED,交OC于点P,再得出ED即为EP+BP最短,解答即可
解:如图,连接DE交OC于点P,即点P满足EP+BP最短.
( http: / / www.21cnjy.com / )
如图,延长CD交y轴于点F,则CF⊥y轴,
∵四边形OBCD是菱形,
∵OD=CD=OB=2,
∵∠DOB=60°,则∠DOF=30°,
∴DF=1,OF= ( http: / / www.21cnjy.com / ),
∴D(1, ( http: / / www.21cnjy.com / )),C(3, ( http: / / www.21cnjy.com / )),
设直线DE的解析式为 ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
∴ ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
设直线OC的解析为 ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
∴ ( http: / / www.21cnjy.com / ),则 ( http: / / www.21cnjy.com / ),
由 ( http: / / www.21cnjy.com / ),得 ( http: / / www.21cnjy.com / ),
∴点P的坐标为 ( http: / / www.21cnjy.com / ).
【考点】翻折变换(折叠问题);三角形的角平分线、中线和高;等腰直角三角形;正方形的性质.
【分析】先连接EC、EE′,设EE′交 ( http: / / www.21cnjy.com )AD于N,根据正方形的性质以及折叠的性质,求出NE、ND的长,以及正方形ABCD的对角线长和边长,再根据CF是△ACE的中线,求出△ACF的面积,根据E′F是△AE′E的中线,求出△AE′F的面积,最后根据四边形CDE′F的面积=S梯形ACDE′﹣S△ACF﹣S△AE′F进行计算,即可解决问题.
解:连接EE′,交AD于N,连接CE,
在正方形ABCD中,∠EDN=45°,
由折叠得,AD垂直平分EE′,且∠EDN=∠E′DN=45°,DE=DE′,
∴△DEE′、△DEN、△DE′N均为等腰直角三角形,
∵DE=2 ( http: / / www.21cnjy.com / ), ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ),
∴OE= ( http: / / www.21cnjy.com / ),DN=EN=E′N=2,DO=3 ( http: / / www.21cnjy.com / ),DE′=2 ( http: / / www.21cnjy.com / ),
∴AC=6 ( http: / / www.21cnjy.com / ),AD=6,
∵EO⊥AC,
∴S△ACE= ( http: / / www.21cnjy.com / )×6 ( http: / / www.21cnjy.com / )× ( http: / / www.21cnjy.com / )=6,
又∵点F是AE的中点,
∴S△ACF= ( http: / / www.21cnjy.com / )×S△ACE=3,
∵AN⊥EE′,AN=AD﹣DN=6﹣2=4,
∴S△AE′E= ( http: / / www.21cnjy.com / )×4×4=8,
又∵点F是AE的中点,
∴S△AE′F= ( http: / / www.21cnjy.com / )×S△AE′E=4,
∵∠E′DO=∠AOD=90°,
∴DE′∥AC,
∴S梯形ACDE′= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )=24,
∴四边形CDE′F的面积=S梯形ACDE′﹣S△ACF﹣S△AE′F=24﹣3﹣4=17.
故答案为:17
( http: / / www.21cnjy.com / )
三 、解答题
【考点】菱形的性质;全等三角形的判定.
【分析】由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由SAS证明△ADE≌△CDF即可.2-1-c-n-j-y
证明:∵四边形ABCD是菱形,
∴AD=CD,
∵点E、F分别为边CD、AD的中点,
∴AD=2DF,CD=2DE,
∴DE=DF,
在△ADE和△CDF中, ( http: / / www.21cnjy.com / ),
∴△ADE≌△CDF(SAS).
【点评】此题主要考查了全等三角形的判定、菱形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.21·世纪*教育网
【考点】全等三角形的判定与性质
【分析】根据矩形的性质得出AB=CD,∠B=∠C=90°,求出BE=CF,根据SAS推出△ABE≌△DCF即可;21*cnjy*com
解: ∵四边形ABCD是矩形.
∴AB=CD ∠ABC=∠DCB
∵BF=CE
∴BC-BF=BC-CE
即BE=FC
∴△ABE≌△DCF(SAS)
∴AE=DF
【考点】菱形的性质;全等三角形的判定与性质;勾股定理
【分析】(1)根据四边形ABCD是菱形 ( http: / / www.21cnjy.com ),判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=6,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少【出处:21教育名师】
解:(1)∵四边形ABCD为菱形,∴AD∥BC,AO=CO. ∴∠MAO=∠NCO.
在△AOM与△CON中, ( http: / / www.21cnjy.com / )∴△AOM≌△CON.∴OM=ON.
(2)依题意,DE∥AC,又AC⊥ ( http: / / www.21cnjy.com )BD,AD∥BC,∴四边形ACED为平行四边形,DE⊥BD.∴CE=AD=AB=BC=6,DE=AC=8.21教育名师原创作品
∴在Rt△BDE中,由勾股定理,得 ( http: / / www.21cnjy.com / ).
∴△BDE的周长为BD+BE+DE= ( http: / / www.21cnjy.com / )+20.
【考点】全等三角形的判定与性质;正方形的性质
【分析】(1)由图示得出∠DAG,∠AFB,∠CDE与∠AED相等;
(2)根据SAS证明△DAE与△ABF全等,利用全等三角形的性质即可证明.
解:(1)与∠AED相等的角有 ( http: / / www.21cnjy.com / ).
(2)选择 ( http: / / www.21cnjy.com / ):
正方形ABCD中, ( http: / / www.21cnjy.com / ),
又∵AF=DE,∴ ( http: / / www.21cnjy.com / ).∴ ( http: / / www.21cnjy.com / ).
或选择∠DAG=∠AED,证明如下:
∵正方形ABCD,
∴∠DAB=∠B=90°,AD=AB,
∵AF=DE,
∴△DAE≌△ABF(SAS),
∴∠ADE=∠BAF,
∵∠DAG+∠BAF=90°,∠GDA+∠AED=90°,
∴∠DAG=∠AED.
【考点】全等三角形的判定与性质;正方形的性质..
【分析】(1)由正方形的性质得出AB=C ( http: / / www.21cnjy.com )B,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,由SAS证明△ABG≌△CBE,得出对应边相等即可;www.21-cn-jy.com
(2)由△ABG≌△CBE,得出对应 ( http: / / www.21cnjy.com )角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
(1)证明:∵四边形ABCD、BEFG均为正方形,
∴AB=CB,∠ABC=∠GBE=90°,BG=BE,
∴∠ABG=∠CBE,
在△ABG和△CBE中, ( http: / / www.21cnjy.com / ),
∴△ABG≌△CBE(SAS),
∴AG=CE;
(2)证明:如图所示:∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠ABC=90°,
∴∠BAG+∠AMB=90°,
∵∠AMB=∠CMN,
∴∠BCE+∠CMN=90°,
∴∠CNM=90°,
∴AG⊥CE.
( http: / / www.21cnjy.com / )
点评:本题考查了正方形的性质、全等三角形的判定与性质、垂线的证法;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.
【考点】矩形的判定;全等三角形的判定与性质.
【分析】(1)根据平行线得出∠CED=∠BFD,根据AAS推出两三角形全等即可;
(2)根据全等得出DE=DF,根据BD=DC推出四边形是平行四边形,求出∠BEC=90°,根据矩形的判定推出即可.
(1)证明:∵CE∥BF,
∴∠CED=∠BFD,
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中
( http: / / www.21cnjy.com / ),
∴△BDF≌△CDE(AAS);
(2)四边形BFCE是矩形,
证明:∵△BDF≌△CDE,
∴DE=DF,
∵BD=DC,
∴四边形BFCE是平行四边形,
∵BD=CD,DE= ( http: / / www.21cnjy.com / )BC,
∴BD=DC=DE,
∴∠BEC=90°,
∴平行四边形BFCE是矩形.
【点评】本题考查了平行线性质,全等三角形的性质和判定,矩形的判定,平行四边形的判定的应用,注意:有一个角是直角的平行四边形是矩形.
【考点】正方形的判定;全等三角形的判定与性质;等腰三角形的性质.
【分析】(1)利用等腰三角形的性质,可得到∠B=∠C,D又是BC的中点,利用AAS,可证出:△BED≌△CFD.
(2)利用(1)的结论可知,DE=DF,再加上三个角都是直角,可证出四边形DFAE是正方形.
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,
∴∠B=∠C.
∵D是BC的中点,
∴BD=CD.
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,
∴四边形DFAE为矩形.
∵△BED≌△CFD,
∴DE=DF.
∴四边形DFAE为正方形.
【点评】本题利用了全等三角形的判定和性 ( http: / / www.21cnjy.com )质以及矩形、正方形的判定.解答此题的关键是利用等腰三角形的两个底角相等,从而证明Rt△BED和Rt△CFD中的两个锐角对应相等.
【考点】四边形综合题.
【分析】(1)①只要证明四边形ABCD是正方形即可解决问题;
②只要证明△ABD≌△CBD,即可解决问题;
(2)若EF⊥BC,则AE≠E ( http: / / www.21cnjy.com )F,BF≠EF,推出四边形ABFE表示等腰直角四边形,不符合条件.若EF与BC不垂直,①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,分别求解即可;
解:(1)①∵AB=AC=1,AB∥CD,
∴S四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形,
∵∠ABC=90°,
∴四边形ABCD是正方形,
∴BD=AC= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / ).
(2)如图1中,连接AC、BD.
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD,
∵BD=BD,
∴△ABD≌△CBD,
∴AD=CD.
(2)若EF⊥BC,则AE≠EF,BF≠EF,
∴四边形ABFE表示等腰直角四边形,不符合条件.
若EF与BC不垂直,
①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,
∴AE=AB=5.
②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,
∴BF=AB=5,
∵DE∥BF,
∴DE:BF=PD:PB=1:2,
∴DE=2.5,
∴AE=9﹣2.5=6.5,
综上所述,满足条件的AE的长为5或6.5.
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
