5.3 正方形（2）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.3 正方形（2）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
正方形的性质
①正方形的四条边都相等，四个角都是直角；
②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；
③正方形具有四边形、平行四边形、矩形、菱形的一切性质．
④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．
基础知识和能力拓展训练
一、选择题
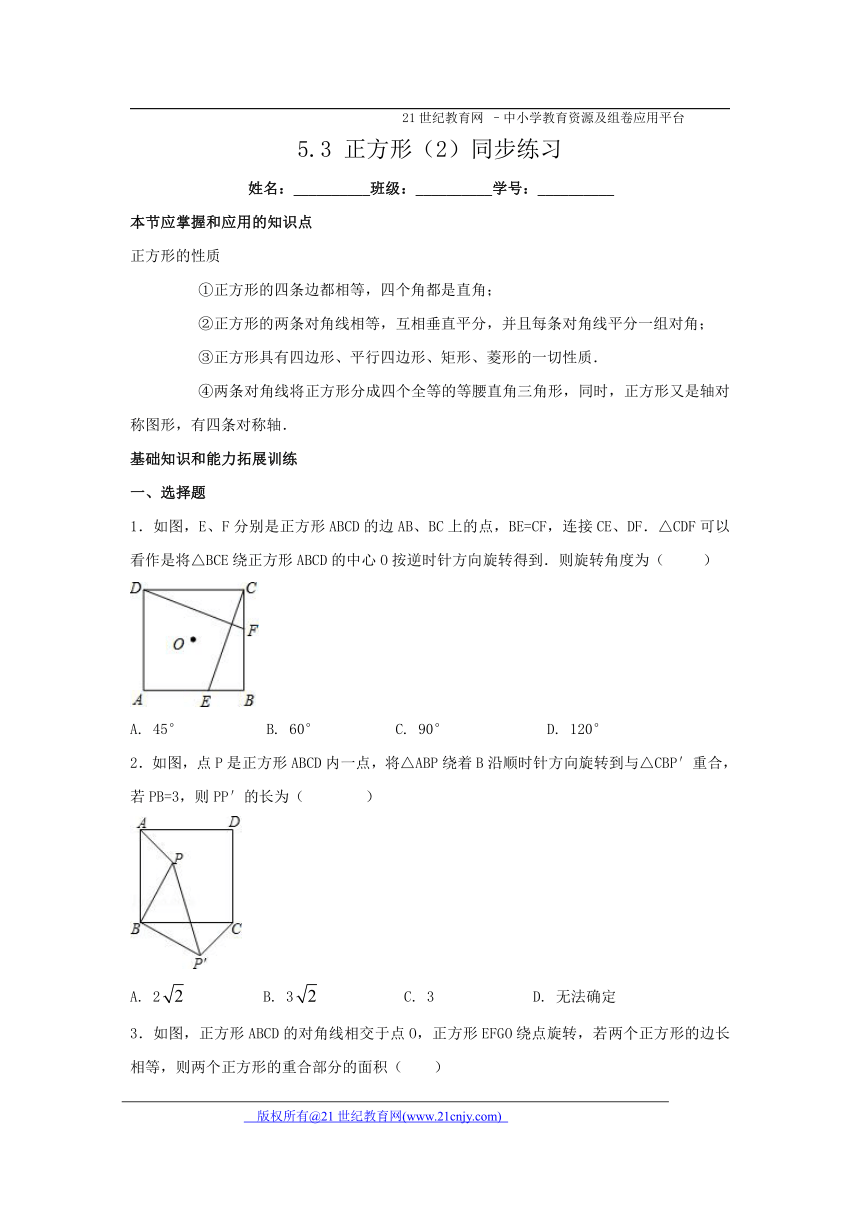
1．如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到．则旋转角度为（ ）
A. 45° B. 60° C. 90° D. 120°
2．如图，点P是正方形ABCD内一点，将△ABP绕着B沿顺时针方向旋转到与△CBP′重合，若PB=3，则PP′的长为（　 　）
A. 2 B. 3 C. 3 D. 无法确定
3．如图，正方形ABCD的对角线相交于点O，正方形EFGO绕点旋转，若两个正方形的边长相等，则两个正方形的重合部分的面积（　　）
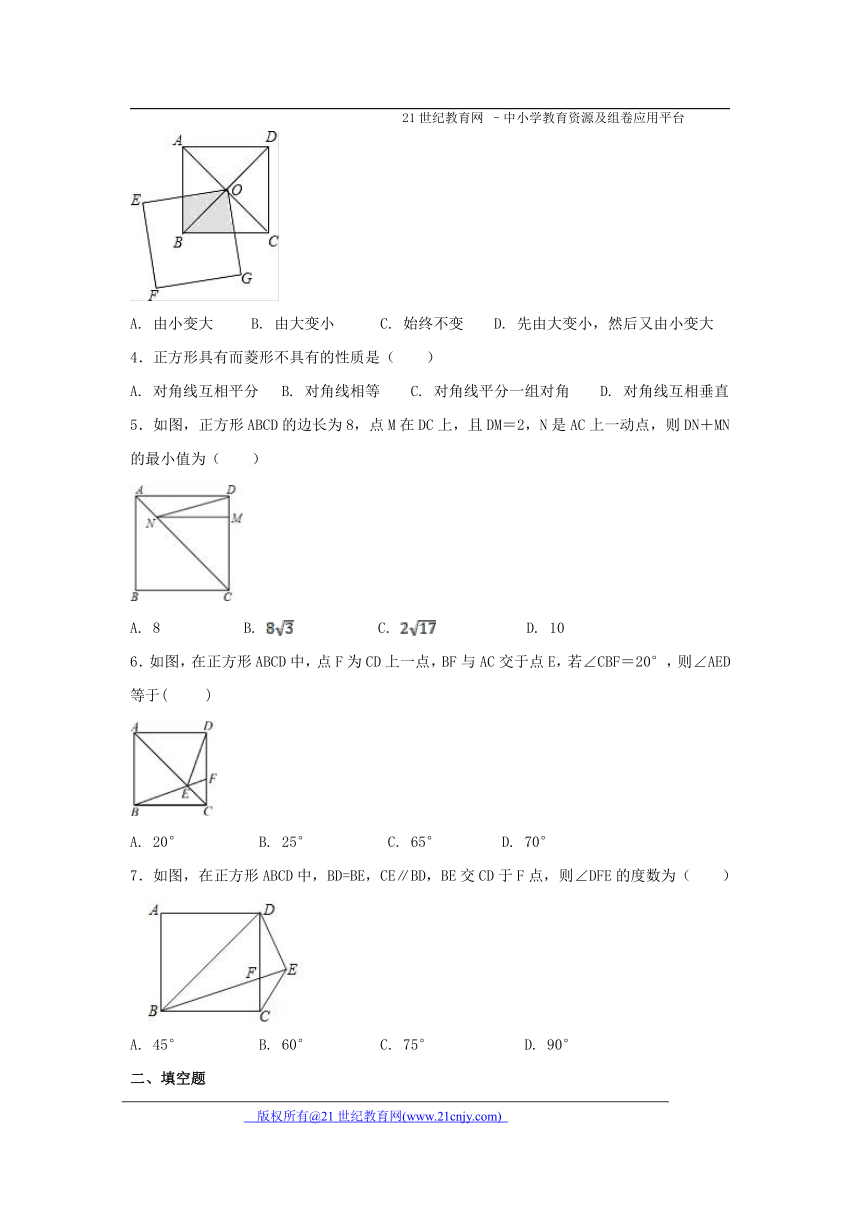
A. 由小变大 B. 由大变小 C. 始终不变 D. 先由大变小，然后又由小变大
4．正方形具有而菱形不具有的性质是（　　）
A. 对角线互相平分 B. 对角线相等 C. 对角线平分一组对角 D. 对角线互相垂直
5．如图，正方形ABCD的边长为8，点M在DC上，且DM＝2，N是AC上一动点，则DN＋MN的最小值为（ ）
A. 8 B. C. D. 10
6．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，若∠CBF＝20°，则∠AED等于(　 　)
A. 20° B. 25° C. 65° D. 70°
7．如图，在正方形ABCD中，BD=BE，CE∥BD，BE交CD于F点，则∠DFE的度数为（　　）
A. 45° B. 60° C. 75° D. 90°
二、填空题
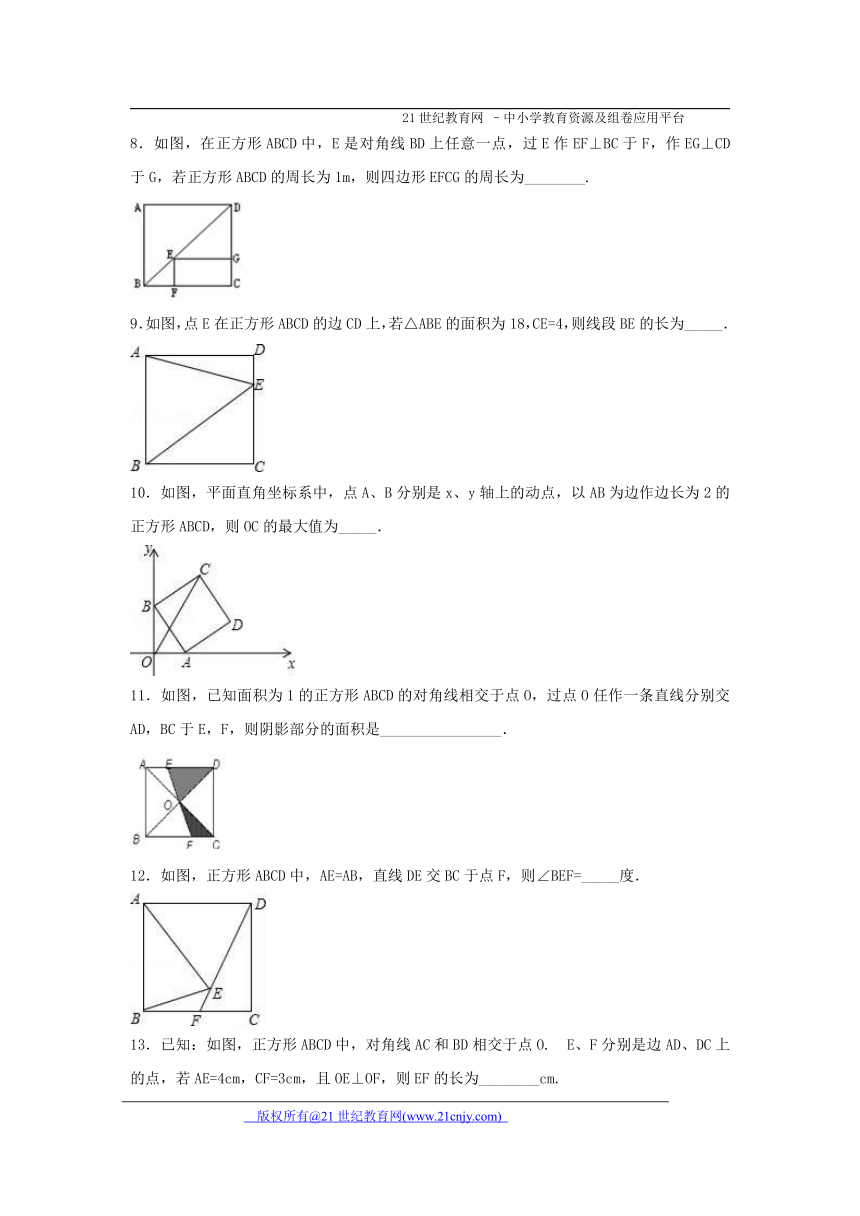
8．如图，在正方形ABCD中，E是对角线BD上任意一点，过E作EF⊥BC于F，作EG⊥CD于G，若正方形ABCD的周长为1m，则四边形EFCG的周长为________.
9．如图，点E在正方形ABCD的边CD上，若△ABE的面积为18，CE=4，则线段BE的长为_____．
10．如图，平面直角坐标系中，点A、B分别是x、y轴上的动点，以AB为边作边长为2的正方形ABCD，则OC的最大值为_____．
11．如图，已知面积为1的正方形ABCD的对角线相交于点O，过点O任作一条直线分别交AD，BC于E，F，则阴影部分的面积是________________．
12．如图，正方形ABCD中，AE=AB，直线DE交BC于点F，则∠BEF=_____度．
13．已知：如图，正方形ABCD中，对角线AC和BD相交于点O. E、F分别是边AD、DC上的点，若AE=4cm，CF=3cm，且OE⊥OF，则EF的长为________cm.
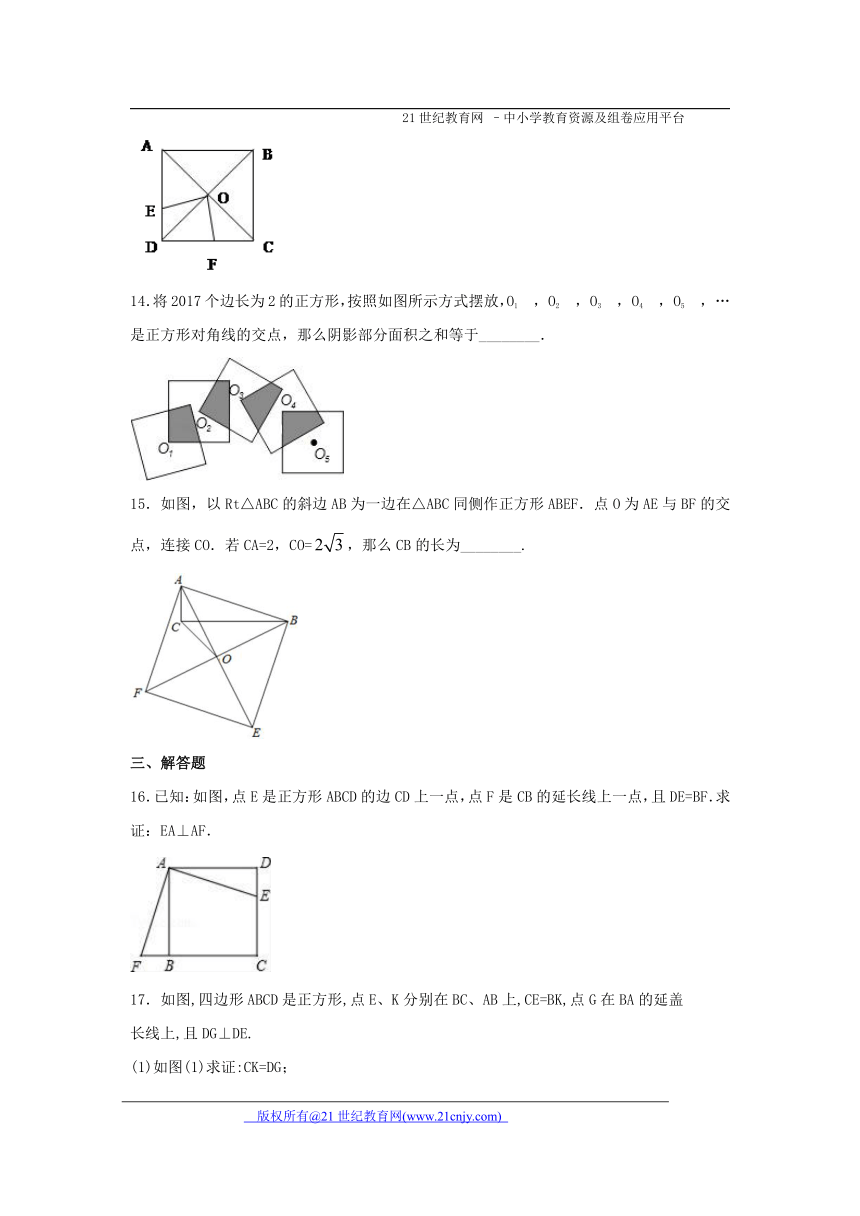
14．将2017个边长为2的正方形，按照如图所示方式摆放，O1 ， O2 ， O3 ， O4 ， O5 ， …是正方形对角线的交点，那么阴影部分面积之和等于________．
15．如图，以Rt△ABC的斜边AB为一边在△ABC同侧作正方形ABEF．点O为AE与BF的交点，连接CO．若CA=2，CO=，那么CB的长为________.
三、解答题
16．已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且DE=BF．求证：EA⊥AF．
17．如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖
长线上,且DG⊥DE.
(1)如图(1)求证:CK=DG；
(2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等
的三角形。
图1 图2
18．如图，已知正方形ABCD中，AE∥BD，BE=BD，BE交AD于F. 求证：DE=DF.
19．如图，已知E是正方形ABCD的边CD外的一点，△DCE为等边三角形，BE交对角线AC于F .
（1）求∠AFD的度数；
（2）求证：AF = EF.
20．如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF．
（1）求证：△BCE≌△DCF；
（2）若∠BEC=60°，求∠EFD的度数．
21．如图1，点为正方形的中心。
（1）将线段绕点逆时针方向旋转，点的对应点为点，连接， ， ，请依题意补全图1；
（2）根据图1中补全的图形，猜想并证明与的关系；
（3）如图2，点是中点，△是等腰直角三角形， 是的中点， ， ， ，△绕点逆时针方向旋转角度，请直接写出旋转过程中的最大值。
参考答案
1．C
【解析】∵将△CBE绕正方形的对角线交点O按顺时针方向旋转到△CDF时，C和D重合，
∴∠COD是旋转角，
∵四边形ABCD是正方形，
∴∠OCD=∠ODC=45°，
∴∠COD=180°-45°-45°=90°，
即旋转角是90°，
故选C.
点睛：本题主要考查了旋转的性质，以及正多边形的性质，正确理解正多边形的性质以及旋转角（对应点与旋转中心所连线段的夹角等于旋转角）是解题的关键．
2．B
【解析】由旋转的性质，得
BP′=BP=3，∠PBP′=∠ABC=90°．
在Rt△PBP′中，由勾股定理，得
PP′=，
故选：B．
3．C
【解析】重叠部分面积不变，总是等于正方形面积的．
理由如下：
∵四边形ABCD和四边形OEFG都是正方形，
∴OB=OC，∠OBC=∠OCD=45°，∠BOC=∠EOG=90°，
∴∠BON=∠MOC．
在△OBN与△OCM中，
∠OBC=∠OCD,
OB=OC,
∠BON=∠MOC，
∴△OBN≌△OCM（ASA），
∴四边形OMCN的面积等于△BOC的面积，
即重叠部分面积不变，总是等于正方形面积的．
故选C．
点睛：本题考查对正方形的性质，全等三角形的性质和判定等知识点的理解和掌握，能推出四边形OMCN的面积等于△BOC的面积是解此题的关键．
4．B
【解析】正方形和菱形都满足：四条边都相等，对角线平分一组对角，对角线垂直且互相平分；
菱形的对角线不一定相等，而正方形的对角线一定相等，
故选B．
5．D
【解析】试题解析：根据题意，连接BD、BM，则BM就是所求DN+MN的最小值，
在Rt△BCM中，BC=8，CM=6，
根据勾股定理得：
即DN+MN的最小值是10；
故选D.
6．C
【解析】解：∵正方形ABCD，∴AB=AD，∠BAE=∠DAE．在△ABE与△ADE中，∵，∴△ABE≌△ADE（SAS），∴∠AEB=∠AED，∠ABE=∠ADE．∵∠CBF=20°，∴∠ABE=70°，∴∠AED=∠AEB=180°﹣45°﹣70°=65°．故选C．
点睛：本题考查了正方形的性质，关键是根据正方形的性质得出∠BAE=∠DAE，再利用全等三角形的判定和性质解答．
7．C
【解析】试题分析：把△BCE逆时针旋转90°得到△BAG，连接DG、AC、AG，则∠BAG=∠BCE，BG=BE，∠GBE=90°，先证出C、A、G三点共线，得出∠DAG=135°，∠BAG=∠DAG，由SAS证明△BAG和△DAG全等，得出BG=DG，证出BG=DG=BE，即△BDG是等边三角形，得出∠GBD=60°，∠DBE=30°，再由三角形的外角的性质求出∠DFE的度数，故选C．
8．m
【解析】∵ABCD为正方形，
∴∠DBC=∠BDC=45°，AB=BC=CD=AD，
又∵EF⊥BC，EG⊥CD，
∴∠EFC=∠EGC=90°，又∠C=90°，
∴四边形EFCG为矩形，
∴EG=FC，EF=GC，
∵△BEF和△EDG都为等腰直角三角形，
∴DG=EG，EF=BF，
则四边形EFCG的周长=EF+FC+CG+EG=DG+GC+CF+FB=DC+BC= (m)．
故答案为： m．
点睛：此题考查了正方形的性质，矩形的判定与性质，以及等腰三角形的性质．根据题意得出△BEF和△EDG都为等腰直角三角形及四边形EFCG为矩形是解本题的关键．
9．
【解析】设正方形边长为a，
∵S△ABE=18，
∴S正方形ABCD=2S△ABE=36，
∴a2=36，
∵a＞0，
∴a=6，
在RT△BCE中，∵BC=6，CE=4，∠C=90°，
∴BE===．
故答案为：．
点睛：本题考查了正方形的性质、三角形的面积公式、勾股定理等知识，解题是关键是理解正方形面积是△ABE面积的2倍
10．
【解析】如图，取AB的中点E，连接OE、CE，
则BE=×2=1，
在Rt△BCE中，由勾股定理得，CE=,
∵∠AOB=90°，点E是AB的中点，
∴OE=BE=1，
由两点之间线段最短可知，点O、E、C三点共线时OC最大，
∴OC的最大值=+1．
故答案为： +1．
【点睛】运用了正方形的性质，直角三角形斜边上的中线等于斜边的一半的性质，勾股定理，熟记各性质并确定出OC最大时的情况是解题的关键．
11．
【解析】试题解析：依据已知和正方形的性质及全等三角形的判定可知△AOE≌△COF，
则得图中阴影部分的面积为正方形面积的，
因为正方形的边长为1，
则其面积为1，
于是这个图中阴影部分的面积为．
故答案为： .
12．45
【解析】解：设∠BAE=x°．∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD．∵AE=AB，∴AB=AE=AD，∴∠ABE=∠AEB=（180°﹣∠BAE）=90°﹣x°，∠DAE=90°﹣x°，∠AED=∠ADE=（180°﹣∠DAE）=[180°﹣（90°﹣x°）]=45°+x°，∴∠BEF=180°﹣∠AEB﹣∠AED=180°﹣（90°﹣x°）﹣（45°+x°）=45°．故答案为：45．
点睛：本题考查了三角形的内角和定理的运用，等腰三角形的性质的运用，正方形性质的应用，解答此题的关键是如何把已知角的未知角结合起来，题目比较典型，但是难度较大．
13．5
【解析】试题解析：连接EF，
∵OD=OC，
∵OE⊥OF
∴∠EOD+∠FOD=90°
∵正方形ABCD
∴∠COF+∠DOF=90°
∴∠EOD=∠FOC
而∠ODE=∠OCF=45°
∴△OFC≌△OED，
∴OE=OF，CF=DE=3cm，则AE=DF=4，
根据勾股定理得到EF==5cm．
故答案为5．
14．2016
【解析】解：由题意可得阴影部分面积等于正方形面积的，则一个阴影部分面积为：1．
n个这样的正方形重叠部分（阴影部分）的面积和为×（n﹣1）×4=（n﹣1）．
所以这个2017个正方形重叠部分的面积和=×（2017﹣1）×4=2016．故答案为：2016．
点睛：本题考查了正方形的性质，解决本题的关键是得到n个这样的正方形重叠部分（阴影部分）的面积和的计算方法，难点是求得一个阴影部分的面积．
15．+2
【解析】如图，在BC上截取BD=AC=2，连接OD，
∵四边形AFEB是正方形，
∴AO=BO，∠AOB=∠ACB=90°，
∴∠CAO=90°-∠ACH，∠DBO=90°-∠BHO，
∵∠ACH=∠BHO，
∴∠CAO=∠DBO，
∴△ACO≌△BDO，
∴DO=CO=，∠AOC=∠BOD，
∵∠BOD+∠AOD=90°，
∴∠AOD+∠AOC=90°，即∠COD=90°，
∴CD=，
∴BC=BD+CD=.
故答案为： .
点睛：本题的解题要点是，通过在BC上截取BD=AC，并结合已知条件证△ACO≌△BDO来证得△COD是等腰直角三角形，这样即可求得CD的长，从而使问题得到解决.
16．见解析
【解析】试题分析：根据条件可以得出AD=AB，∠ABF=∠ADE=90°，从而可以得出△ABF≌△ADE，就可以得出∠FAB=∠EAD，就可以得出结论．
试题解析：
证明：∵四边形ABCD是正方形，
∴AB=AD，∠ABC=∠D=∠BAD=90°，
∴∠ABF=90°．
∵在△BAF和△DAE中，
，
∴△BAF≌△DAE（SAS），
∴FAB=∠EAD，
∵∠EAD+∠BAE=90°，
∴∠FAB+∠BAE=90°，
∴∠FAE=90°，
∴EA⊥AF．
17．（1）证明见解析；（2）ΔGKD,ΔCKD,ΔKGC,ΔDGC.
【解析】试题分析：（1）依据正方形的性质，判定△DCE≌△CBK，即可得到DE=CK，再判定△ADG≌△CDE，即可得到DG=DE，进而得出DG=CK；
（2）依据△DCE≌△CBK，可得S△DCE=S△BCK，进而得到S四边形BEFK=S△CDF，进而得出S四边形BEDK=S△CDK，再根据四边形CDGK是平行四边形，即可得到S△CDK=S△CDG=S△GDK=S△CGK．
试题解析：解：（1）如图1．∵四边形ABCD是正方形，∴DC=CB=AD，∠B=∠DCE=∠DAG=90°．∵CE=BK，∴△DCE≌△CBK，∴DE=CK．∵DG⊥DE，∴∠ADG+∠ADE=90°=∠CDE+∠ADE，∴∠ADG=∠CDE．又∵∠DAG=∠DCE=90°，AD=CD，∴△ADG≌△CDE，∴DG=DE，∴DG=CK；
（2）如图2．∵△DCE≌△CBK，∴S△DCE=S△BCK，∴S四边形BEFK=S△CDF，∴S四边形BEFK+S△DFK=S△CDF+S△DFK，即S四边形BEDK=S△CDK．∵△ADG≌△CDE，∴CE=BK=AG，∴CD=AB=GK．又∵DG=CK，∴四边形CDGK是平行四边形，∴S△CDK=S△CDG=S△GDK=S△CGK，∴与四边形BEDK面积相等的三角形为△CDK，△CDG，△GDK，△GCK．
点睛：本题考查了正方形的性质、全等三角形的判定与性质以及平行四边形的性质与判定．证得△DCE≌△CBK，△ADG≌△CDE以及四边形CDGK是平行四边形是解答此题的关键．
18．见解析
【解析】试题分析：连接AC，交BD于点O，作EG⊥BD于点G，则可知四边形AOGE是矩形，可证得EG=BD=E，所以∠EBD=30°，结合条件可求得∠BED=75°，∠EFD=∠FDB+∠EBD=45+30=75°，故∠DEF=∠DFE，即可得到DF=DE．
试题解析：
证明：连接AC，交BD于点O，作EG⊥BD于点G．如图所示：
∵四边形ABCD是正方形，
∴AC⊥BD，
∵AE∥BD，
∴四边形AOGE是矩形，
∴EG=AO=AC=BD=BE，
∴∠EBD=30°，
∵∠EBD=30°，BE=BD，
∴∠BED=75°，
∵∠EFD=∠FDB+∠EBD=45+30=75°，
∴∠DEF=∠DFE，
∴DF=DE．
19．∠AFD=60°；（2）证明见解析.
【解析】整体分析：
（1）用正方形和等边三角形的性质得△CDF≌△CBF，由△CBE是等腰三角形，求∠CBE的度数即可；（2）用SAS证明△ADF≌△EDF.
（1）解：∵四边形ABCD是正方形，
∴CB=CD=DA=DE，∠BCF=∠DCF=45°，∠BCD=90°，
∵CF=CF，
∴△CDF≌△CBF，
∴∠CDF=∠CBE，
∵△CDE是等边三角形，∴CB=CE，∠DCE=60°，
∴∠CBE=（180°-90°-60°）÷2=15°，
∴∠CDF=15°.
∴∠AFD=∠ACD+∠CDF=45°+15°=60°.
(2)证明：∵DA=DE，∠ADF=∠EDF=75°，DF=DF，
∴△ADF≌△EDF，
∴AF=EF.
20．(1)见解析；（2）15°
【解析】试题分析：（1）可利用边角边证明BE、DF所在的两个直角三角形全等，进而证明这两条线段相等；
（2）由（1）中的全等可得∠DFC=∠BEC=60°，易得∠CFE=45°，相减即可得到所求角的度数．
试题解析：（1）证明：∵ABCD是正方形，
∴DC=BC，∠DCB=∠FCE，
∵CE=CF，
∴△DCF≌△BCE；
（2）∵△BCE≌△DCF，
∴∠DFC=∠BEC=60°，
∵CE=CF，
∴∠CFE=45°，
∴∠EFD=15°．
点睛：综合考查了正方形的性质及全等三角形的判定与性质．用到的知识点为：考查两条线段的大小关系，一般考虑相等，证明这两条线段所在的三角形的全等是常用的方法．
21．（1）图形见解析（2）证明见解析（3）
【解析】（1）根据题意画出图形即可；
（2）延长EA交OF于点H，交BF于点G，利用正方形的性质和旋转的性质证明△EOA≌△FOB，得到AE=BF．根据等边对等角得到∠OEA=∠OFB，由∠OEA+∠OHA=90°，所以∠OFB+∠FHG=90°，进而得到AE⊥BF．
（3）BH的最大值为.
解：（1）正确画出图形，如下图所示：
（2）延长EA交OF于点，交于点
∵为正方形的中心，
∴，∠＝90，
∵绕点逆时针旋转90角得到，
∴，
∴∠＝∠＝90，
∴∠＝∠，
在△和△中，
，
∴△≌△，
∴，
∴∠＝∠，
∵∠+∠，
∴∠+∠=90，
∴⊥;
（3）的最大值为.
点睛：本题主要考查正方形和旋转的性质.根据图形灵活应用几何性质是解题的关键.
版权所有@21世纪教育网(www.21cnjy.com)