5.2 菱形（1）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.2 菱形（1）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
（1）菱形的定义：有一组邻边相等的平行四 ( http: / / www.21cnjy.com )边形叫做菱形．
（2）菱形的性质
①菱形具有平行四边形的一切性质；
②菱形的四条边都相等；
③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；
④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．
（3）菱形的面积计算
①利用平行四边形的面积公式．
②菱形面积=ab．（a、b是两条对角线的长度）
基础知识和能力拓展训练
一、选择题
1．已知：如图，菱形ABCD对角线AC与BD相交于点O，E为BC的中点E，AD=6cm，则OE的长为（　　）
( http: / / www.21cnjy.com / )
A. 6cm B. 4cm C. 3cm D. 2cm
2．已知：如图，在矩形ABCD中，E ,F ( http: / / www.21cnjy.com ) ,G ,H分别为边AB, BC ,CD, DA的中点．若AB＝2，AD＝4，则图中阴影部分的面积为 ( )21*cnjy*com
( http: / / www.21cnjy.com / )
A. 5 B. 4.5 C. 4 D. 3.5
3．如图，菱形ABCD中，对角线AC、BD相交于点O，下列结论中不一定成立的是（ ）
( http: / / www.21cnjy.com / )
A. AB∥DC B. AC＝BD C. AC⊥BD D. OA＝OC
4．如图四边形ABCD是菱形，对角线AC=8，BD=6，DH⊥AB于点H，则DH的长度是（　　）
( http: / / www.21cnjy.com / )
A. B. C. D.
5．如图，将四根长度相等的细木条首尾相连， ( http: / / www.21cnjy.com )用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当AB=4，∠B=60°时，AC等于 （　　）21·cn·jy·com
( http: / / www.21cnjy.com / )
A. 2 B. 4 C. 2 D. 4
6．如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE=，∠EAF=135°，则以下结论正确的是（　　）21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. DE=1 B. tan∠AFO= C. AF= D. 四边形AFCE的面积为
二、填空题
7．已知菱形两条对角线的长分别为5cm和12cm，则这个菱形的面积是________cm2.
8.如图，在菱形ABCD中， E、F分别是DB、DC的中点，若AB=10，则EF=______.
( http: / / www.21cnjy.com / )
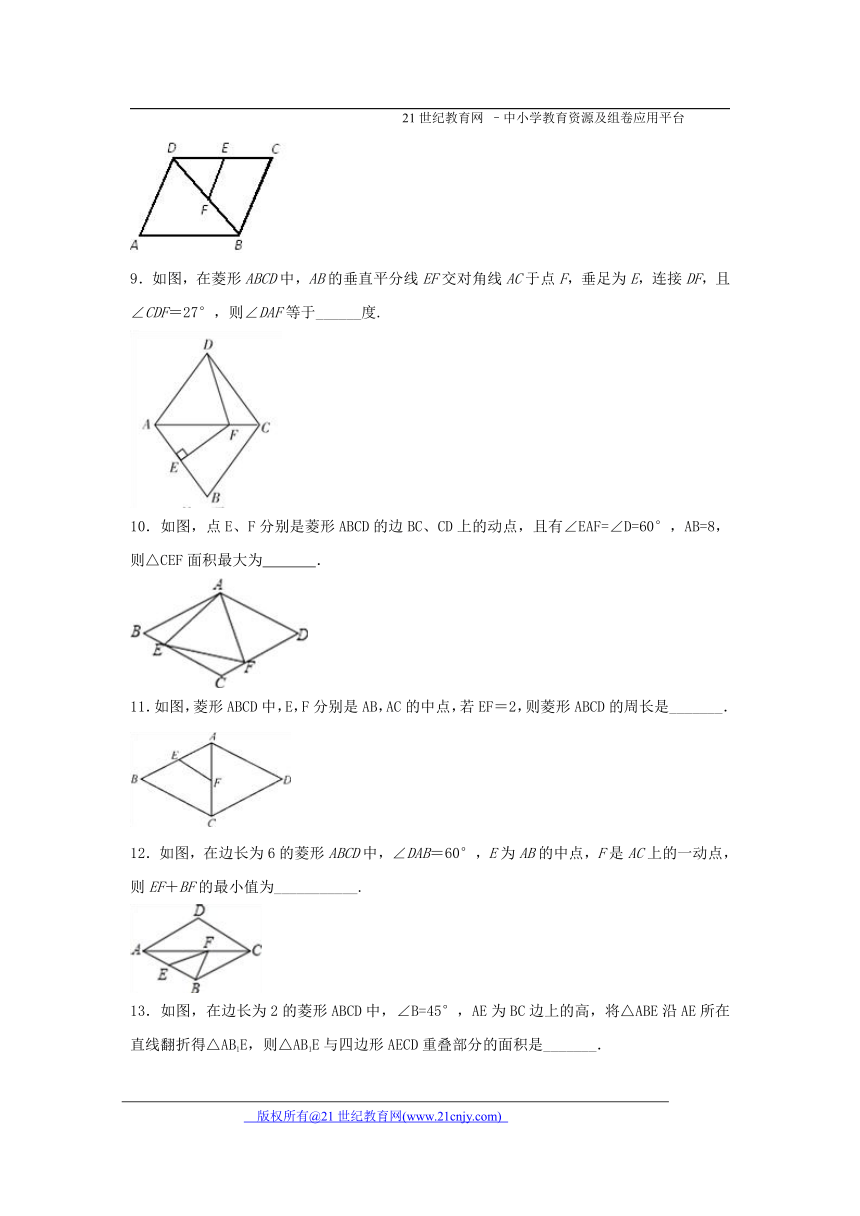
9．如图，在菱形ABCD中，AB的垂直平分线EF交对角线AC于点F，垂足为E，连接DF，且∠CDF＝27°，则∠DAF等于______度.【来源：21·世纪·教育·网】
( http: / / www.21cnjy.com / )
10．如图，点E、F分别是菱形ABCD的边BC、CD上的动点，且有∠EAF=∠D=60°，AB=8，则△CEF面积最大为　 　．21*cnjy*com
( http: / / www.21cnjy.com / )
11．如图，菱形ABCD中，E，F分别是AB，AC的中点，若EF＝2，则菱形ABCD的周长是_______．
( http: / / www.21cnjy.com / )
12．如图，在边长为6的菱 ( http: / / www.21cnjy.com )形ABCD中，∠DAB＝60°，E为AB的中点，F是AC上的一动点，则EF＋BF的最小值为___________.
( http: / / www.21cnjy.com / )
13．如图，在边长为2的菱形ABCD中 ( http: / / www.21cnjy.com )，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB1E，则△AB1E与四边形AECD重叠部分的面积是_______．
( http: / / www.21cnjy.com / )
三、解答题
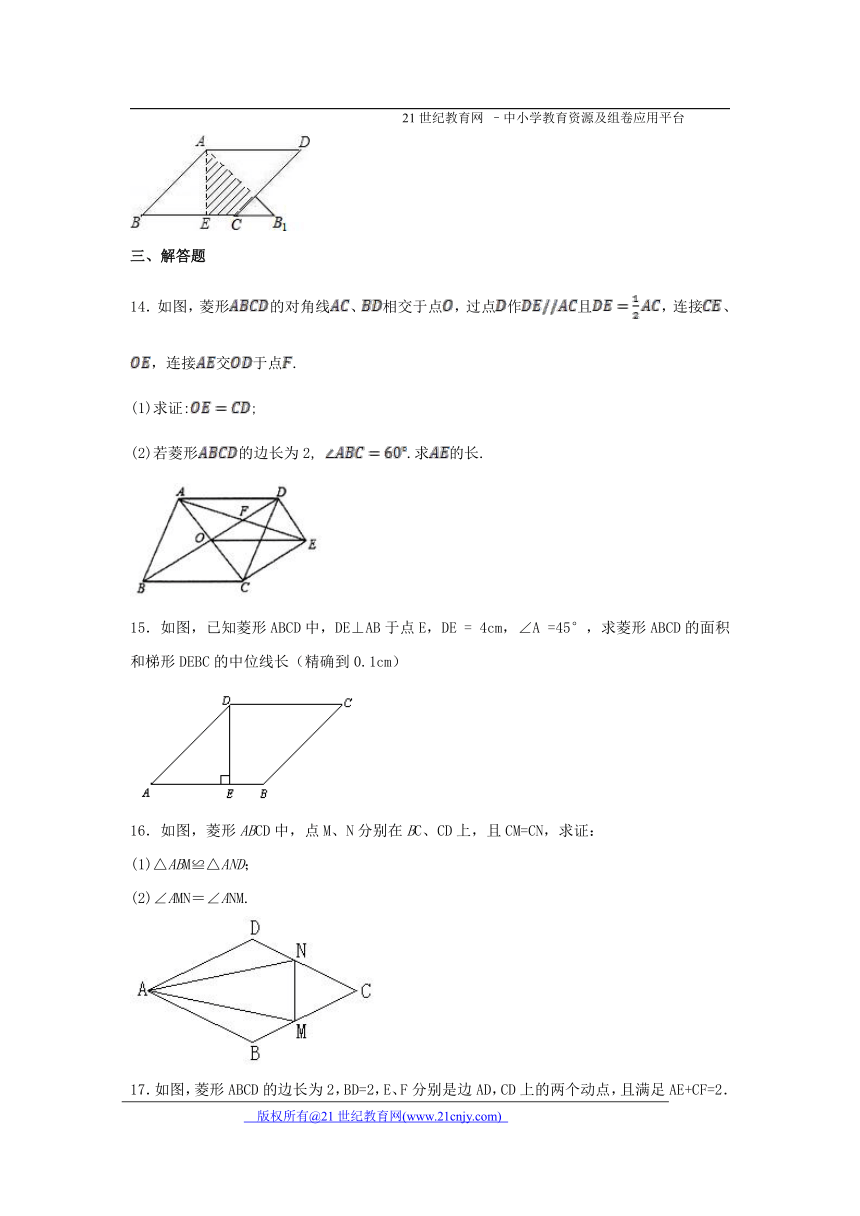
14．如图，菱形的对角线、相交于点，过点作且，连接、，连接交于点.2·1·c·n·j·y
(1)求证:;
(2)若菱形的边长为2, .求的长.
( http: / / www.21cnjy.com / )
15．如图，已知菱形ABCD中，D ( http: / / www.21cnjy.com )E⊥AB于点E，DE = 4cm，∠A =45°，求菱形ABCD的面积和梯形DEBC的中位线长（精确到0.1cm）
( http: / / www.21cnjy.com / )
16．如图，菱形ABCD中，点M、N分别在BC、CD上，且CM=CN，求证：
(1)△ABM≌△AND；
(2)∠AMN＝∠ANM.
( http: / / www.21cnjy.com / )
17．如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2．
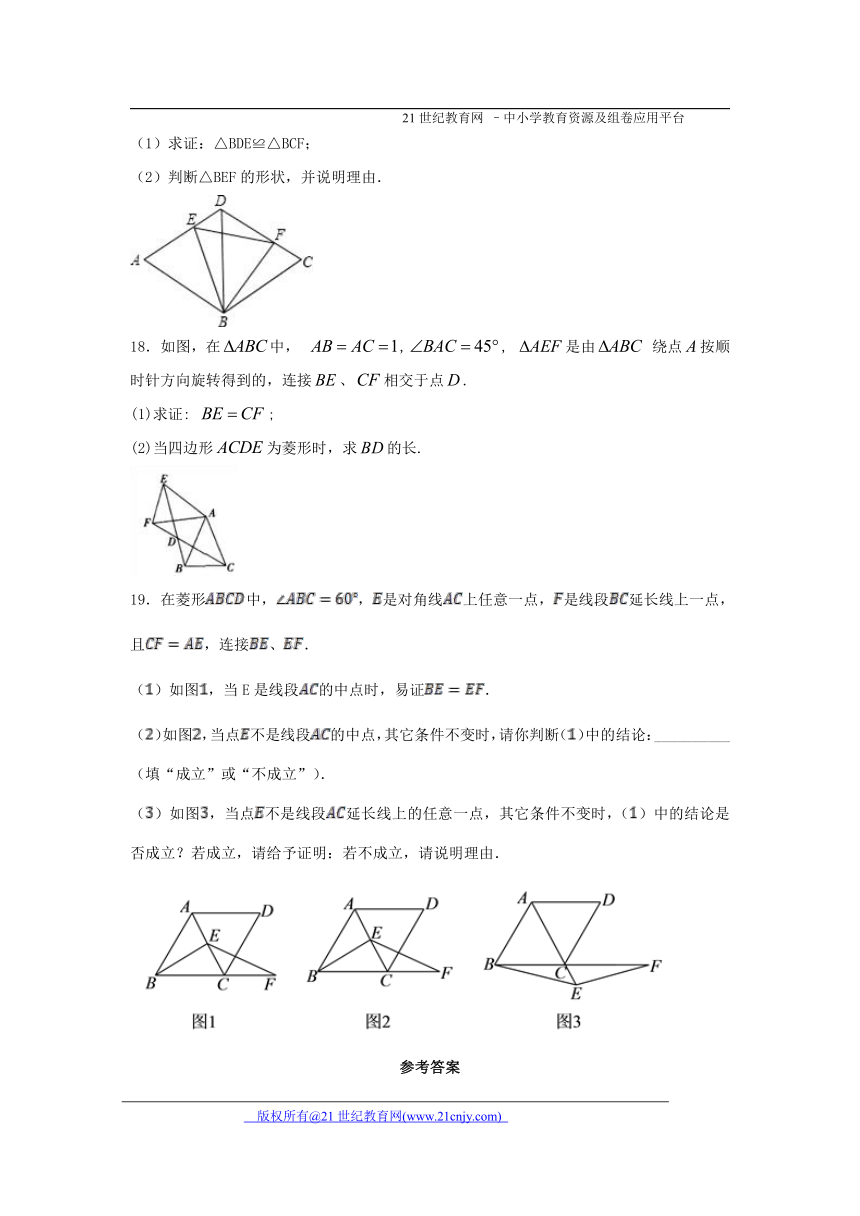
（1）求证：△BDE≌△BCF；
（2）判断△BEF的形状，并说明理由．
( http: / / www.21cnjy.com / )
18．如图，在中， ,, 是由 绕点按顺时针方向旋转得到的，连接、相交于点.
(1)求证: ;
(2)当四边形为菱形时，求的长.
( http: / / www.21cnjy.com / )
19．在菱形中，，是对角线上任意一点，是线段延长线上一点，且，连接、．
（）如图，当E是线段的中点时，易证．
（）如图，当点不是线段的中点，其它条件不变时，请你判断（）中的结论：__________（填“成立”或“不成立”）．
（）如图，当点不是线段延长线上的任意一点，其它条件不变时，（）中的结论是否成立？若成立，请给予证明：若不成立，请说明理由．
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
参考答案
1．C
【解析】∵四边形ABCD是菱形，
∴AO=CO，AB=AD=6cm，
∵E为CB的中点，
∴OE是△ABC的中位线，
∴BA=2OE，
∴OE=3cm．
故选：C．
2．C
【解析】连接AC，BD，FH，EG，
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形，
∴AC=BD，
∵E，F，G，H分别为边AB，BC，CD，DA的中点，
∴HG=AC,EF∥AC,EF=AC,EH=BD，GF=BD，
∴EH=HG =EF=GF，
∴平行四边形EFGH是菱形，
∴FH⊥EG，
∴阴影部分EFGH的面积是×HF×EG=×2×4=4，
故选C.
3．B
【解析】试题解析：∵四边形ABCD是菱形，
∴AB∥DC，故选项A正确，不合题意；
无法得出AC=BD，故选项B错误，符合题意；
AC⊥BD，故选项C正确，不合题意；
OA=OC，故选项D正确，不合题意；
故选B.
点睛：菱形的对角线互相垂直平分,
4．C
【解析】∵四边形ABCD是菱形，AC=8，BD=6，
∴AC⊥BD，OA=OC=4，OB=OD=3，
∴AB=5cm，
∴S菱形ABCD=AC·BD=AB·DH，
∴DH=．
故选C.
5．B
【解析】试题解析：连接AC，
( http: / / www.21cnjy.com / )
∵将四根长度相等的细木条首尾相连，用钉子钉成四边形ABCD，
∴AB=BC，
∵
∴△ABC是等边三角形，
∴AC=AB=4.
故选B.
6．C
【解析】因为四边形ABCD是正方形,所以AB=CB=CD=AD=1,AC⊥BA, ∠ADO=∠ABO=45°,所以OD=OB=OA=, ∠ABF=∠ADE=135°,在Rt△AEO中,根据勾股定理可得:EO=,DE=,所以A错误,因为∠EAF =135°, ∠BAD =90°,所以∠EAF =135°,21·世纪*教育网
∠BAF+∠DAE=45°, 所以∠BAF =∠AED, 所以△ABF ∽△EDA ,所以,,所以BF=,Rt△AOF中,由勾股定理可得:AF=,所以C正确,所以tan∠AFO=,所以B错误,所以,所以D错误,故选C.【出处：21教育名师】
7．30
【解析】菱形的面积=×5×12=30(cm2).
故答案为：30.
8．5
【解析】试题解析：由菱形的性质可知：BC=AB=10，
又∵E、F分别是DB、DC的中点，
∴ (三角形的中位线定理).
故答案为：5.
点睛：三角形的中位线平行于第三边而且等于第三边的一半.
9．51
【解析】如图，连接BF，由菱形的轴 ( http: / / www.21cnjy.com )对称性质得DF=BF，因为EF是AB的垂直平分线，所以BF=AF，所以DF=AF=FB，所以∠FDA=∠FAD=∠FAB，设∠FDA=∠FAD=∠FAB=x，因为∠CDA+∠BAD=180°，所以3x+27°=180°，解得x=51°，故答案为51.
( http: / / www.21cnjy.com / )
10．
【解析】如图，连接AC，
∵四边形ABCD是菱形，且∠EAF=∠D=60°，
∴∠BAC=∠ACF=∠B=60°，AB=BC，
∴∠BAE+∠EAC=∠EAC+∠CAF=60°，△ABC是等边三角形，
∴∠BAE=∠CAF，AB=AC，
∴△ABE≌△ACF，
∴AE=AF，S△ACF=S△ABE，
∴△CEF是等边三角形，S四边形AECF=S△ABC，
∴S△CEF=S△ABC-S△AEF，
∵AB=8，△ABC是等边三角形，
∴S△ABC=，
∴当AE⊥BC，S△AEF的面积最小时，S△CEF最大，
∵当AE⊥BC时，AE=，
∴S△AEF最小=，
∴S△CEF最大=.
故答案为： .
( http: / / www.21cnjy.com / )
11．16
【解析】试题解析：∵E、F分别是AB、AC的中点，
∴EF是△ABC的中位线，
∴BC=2EF=2×2=4，
∴菱形ABCD的周长=4BC=4×4=16．
故答案为16．
12．
【解析】仿照将军饮马的方法求解，如图：由于点 ( http: / / www.21cnjy.com )D和点B关于AC对称，连接DE，则EF＋BF的最小值为DE，在等边三角形ABD中，E为AB的中点，则 ，DE=ADsin60°= .21cnjy.com
故答案：.
( http: / / www.21cnjy.com / )
13．
【解析】解：如图，设CD与AB1交于点O，∵在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，∴AE=，由折叠易得△ABB1为等腰直角三角形，∴S△ABB1=BA AB1=2，S△ABE=1，∴CB1=2BE﹣BC=，∵AB∥CD，∴∠OCB1=∠B=45°，又由折叠的性质知，∠B1=∠B=45°，∴CO=OB1=，∴S△COB1=OC OB1=，∴重叠部分的面积为：2﹣1﹣（）=．2-1-c-n-j-y
( http: / / www.21cnjy.com / )
点睛：此题考查了菱形的性质以及等腰直角三角形的性质．注意掌握数形结合思想的应用．
14．（1）证明见解析（2）
【解析】试题分析：（1）先 ( http: / / www.21cnjy.com )求出四边形OCED是平行四边形，再根据菱形的对角线互相垂直求出∠COD=90°，证明OCED是矩形，可得OE=CD即可；【来源：21cnj*y.co*m】
（2）根据菱形的性质得出AC=AB，再根据勾股定理得出AE的长度即可．
（1）证明：在菱形ABCD中，OC=AC．
∴DE=OC．
∵DE∥AC，
∴四边形OCED是平行四边形．
∵AC⊥BD，
∴平行四边形OCED是矩形．
∴OE=CD．
（2）在菱形ABCD中，∠ABC=60°，
∴AC=AB=2．
∴在矩形OCED中，
CE=OD=．
在Rt△ACE中，
AE=．
点睛：本题考查了菱形的性质，矩形的判定与性质，勾股定理的应用，是基础题，熟记矩形的判定方法与菱形的性质是解题的关键．21教育名师原创作品
15．菱形ABCD的面积是22.7cm ，梯形DEBC的中位线长是3.7cm.
【解析】解：∵四边形ABCD是菱形，
∴AD=DC=AB，
∵DE⊥AB，
∴∠AED=90°，
∵∠A=45°，
∴△ADE是等腰直角三角形，∴AE=DE=4，
由勾股定理得，AD=，
∴AB=，
∴菱形ABCD的面积为DE×AB=4×=≈22.7cm ，
∵BE=-4，CD=AD=，
∴梯形DEBC的中位线长（-4+）÷2=-2≈3.7cm.
答：菱形ABCD的面积是22.7cm ，梯形DEBC的中位线长是3.7cm.
16．（1）证明见解析；（2）证明见解析.
【解析】整体分析：
（1）根据菱形的性质，用SAS证明△ABM≌△AND；（2）由（1）△ABM≌△AND得，AN=AM，根据等角对等边证明.21教育网
证明：⑴∵四边形ABCD是菱形
∴AB＝AD，∠B＝∠D，BC＝DC
又∵CM＝CN
∴BC－CM＝DC－CN即BM＝DN
∵AB＝AD，∠B＝∠D，BM＝DN
∴△ABM≌△ADN（SAS）
⑵∵△ABM≌△ADN
∴AM＝AN
∴∠AMN＝∠ANM
17．（1）证明见解析（2）等边三角形
【解析】试题分析：（1） ( http: / / www.21cnjy.com )由菱形ABCD的边长为2，BD=2，易得BD=BC，∠C=∠BDE=60°，又由AE+CF=2，易得DE=CF，则可证得：△BDE≌△BCF；www-2-1-cnjy-com
（2）由△BDE≌△BCF，易得BE=BF，∠EBF=60°，则可证得△BEF是等边三角形．
试题解析：（1）证明：∵菱形ABCD的 ( http: / / www.21cnjy.com )边长为2，BD=2，∴BC=BD=CD=AD=2，∴∠C=∠CDB=60°．∵∠BDE=∠BDC，∴∠BDE=∠C．∵AE+DE=AD=2，AE+CF=2，∴DE=CF．在△BDE和△BCF中，∵BD=BC，∠BDE=∠C，DE=CF，∴△BDE≌△BCF（SAS）；
（2）解：等边三角形．理由如下：
∵△BDE≌△BCF，∴BE=BF，∠ ( http: / / www.21cnjy.com )CBF=∠DBE．∵∠CBF+∠DBF=60°，∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60°，∴△BEF是等边三角形．
点睛：本题考查了菱形的性质、全等三角形的判定与性质以及等边三角形的判定．注意证得DE=CF，∠BDE=∠C是关键．
18．（1）见解析；（2）
【解析】试题分析：（1）先由旋转的 ( http: / / www.21cnjy.com )性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD；
（2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的性质得∠AEB=∠ABE，根据平行线得性质得∠ABE=∠BAC=45°，所以∠AEB=∠ABE=45°，于是可判断△ABE为等腰直角三角形，所以BE=AC=，于是利用BD=BE-DE求解．
试题解析：（1）证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，
∴AE=AB，AF=AC，∠EAF=∠BAC，
∴∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，
∵AB=AC，
∴AE=AF，
∴△AEB可由△AFC绕点A按顺时针方向旋转得到，
∴BE=CF；
（2）解：∵四边形ACDE为菱形，AB=AC=1，
∴DE=AE=AC=AB=1，AC∥DE，
∴∠AEB=∠ABE，∠ABE=∠BAC=45°，
∴∠AEB=∠ABE=45°，
∴△ABE为等腰直角三角形，
∴BE=AC=，
∴BD=BE-DE=-1．
19．（）证明见解析；（）成立；（）成立，证明见解析.
【解析】(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作 ( http: / / www.21cnjy.com / )交AB的延长线于H,证明 ( http: / / www.21cnjy.com / ),得到 ( http: / / www.21cnjy.com / ).
本题解析：
（）∵菱形，，
∴，，
∵为中点，，
∴，
∴，
∴，
∴，
∴．
（）成立，取，连，
∵菱形，，
∴，，
∵，，
∴为等边三角形．
∴，，
∵，
∴，
在和中，
，
∴≌，
∴．
( http: / / www.21cnjy.com / )
（）成立．
取，连，
由（）得：、均为等边三角形，
∴，，，
∵，
∴，
∴，
在和中，
，
∴≌，
∴．
( http: / / www.21cnjy.com / )
点睛：本题考查了菱形的性质、全等三角形的 ( http: / / www.21cnjy.com )判定与性质、等边三角形的判定与性质;熟练掌握菱形的性质,证明三角形全等和等边三角形是解决问题的关键.【版权所有：21教育】
( http: / / www.21cnjy.com / )
版权所有@21世纪教育网(www.21cnjy.com)