5.2 菱形（2）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.2 菱形（2）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
1.菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等=菱形
2.四条边都相等的四边形是菱形．
几何语言：∵AB=BC=CD=DA∴四边形ABCD是菱形；
3.对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．
几何语言：∵AC⊥BD，四边形ABCD是平行四边形∴平行四边形ABCD是菱形
基础知识和能力拓展训练
一、选择题
1．已知：如图，在矩形ABCD中，E ,F ,G ,H分别为边AB, BC ,CD, DA的中点．若AB＝2，AD＝4，则图中阴影部分的面积为 ( )
A. 5 B. 4.5 C. 4 D. 3.5
2．四边形的四边长顺次为a、b、c、d，且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是（　　）
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
3．如图，在□ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE，CF，则四边形AECF是（　　）
A. 矩形 B. 菱形 C. 正方形 D. 无法确定
4．如图，在 ABCD中，对角线相交于点O，添加下列条件不能判定 ABCD是菱形的只有
A. B. C. D.
5．如图，在四边形中，分别是的中点，要使四边形是菱形，则四边形满足的一个条件是（ ）
A. 四边形是矩形 B. 四边形是菱形 C. D.
6．如图是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：
对于甲、乙两人的作法，可判断(　　)
A. 甲正确，乙错误 B. 甲错误，乙正确 C. 甲、乙均正确 D. 甲、乙均错误
7．一张矩形纸片如图对折两次，然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（　　）
A. 三角形 B. 矩形 C. 菱形 D. 五边形
8．如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( 　)
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
二、填空题
9．在 ABCD中，AB＝5，AC＝6，当BD＝____时，四边形ABCD是菱形．
10．如图，DE∥AC交AB于点E，DF∥AB交AC于F，∠1=∠2,四边形AEDF的形状是__________．
11．如图，将△ABC沿射线BC方向平移得到△DCE，当△ABC满足条件________时(填一个条件)，能够判定四边形ACED为菱形.
12．如图，点D、E、F分别是△ABC三边的中点，且AB=AC，则图中的四边形________是菱形．
13．已知，对角线AC、BD相交于点O.
⑴若AB=BC，则是_______.
⑵若AC=BD，则是_________.
⑶若∠BCD=90°，则是_________.
⑷若OA=OB，且OA⊥OB，则是_________.
⑸若AB=BC，且AC=BD，则是_________.
14．如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是______．
三、解答题
15．已知：在四边形ABCD中，E、F、G、H分别是BC、AD、BD、AC的中点，AB=CD，
EF与GH有什么位置关系？请说明理由。
16．如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．试判断四边形ADCF的形状，并证明你的结论．
17．已知：如图,△和△的顶点在边的同侧, , 交于,∠的平分线交于,延长到,使.
求证：四边形是菱形.
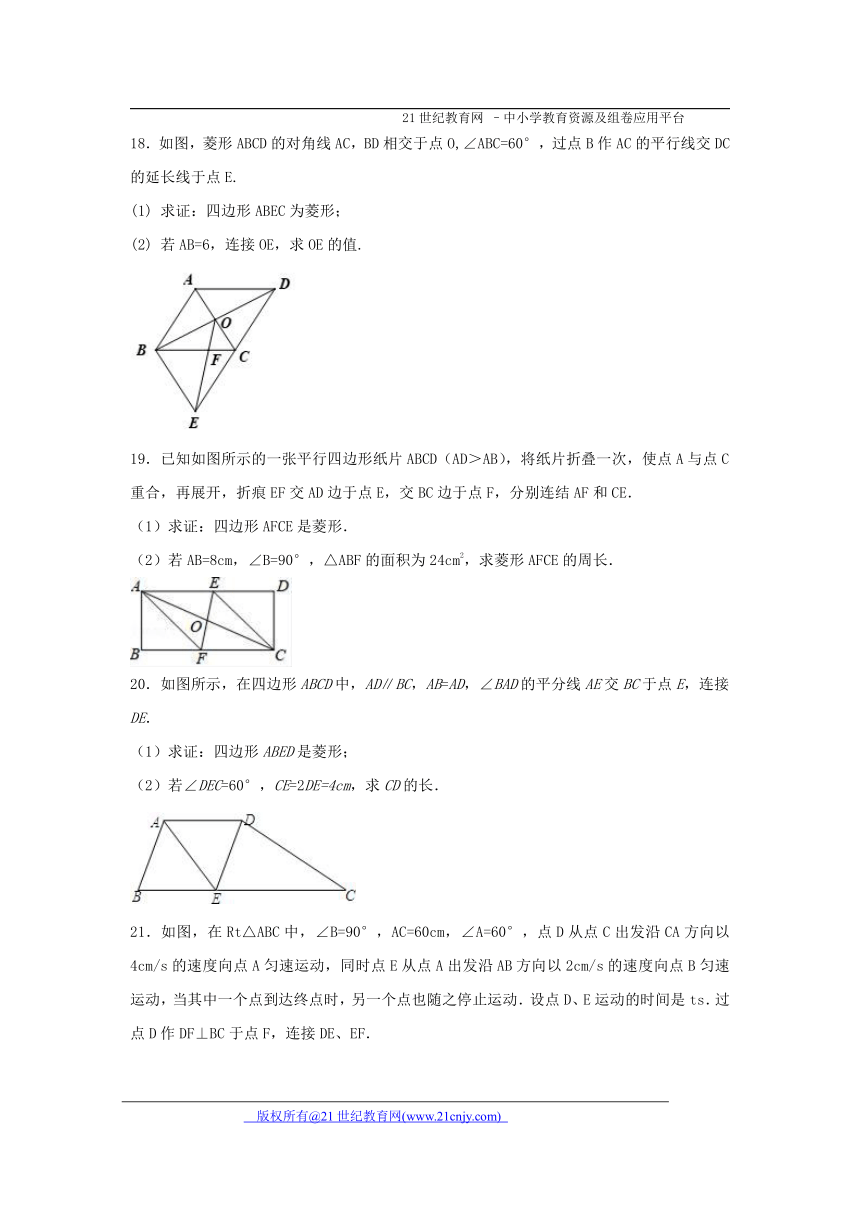
18．如图，菱形ABCD的对角线AC，BD相交于点O,∠ABC=60°，过点B作AC的平行线交DC的延长线于点E.
(1) 求证：四边形ABEC为菱形；
(2) 若AB=6，连接OE，求OE的值.
19．已知如图所示的一张平行四边形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．
（1）求证：四边形AFCE是菱形．
（2）若AB=8cm，∠B=90°，△ABF的面积为24cm2，求菱形AFCE的周长．
20．如图所示，在四边形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．
（1）求证：四边形ABED是菱形；
（2）若∠DEC=60°，CE=2DE=4cm，求CD的长．
21．如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是ts．过点D作DF⊥BC于点F，连接DE、EF．
（1）用t的代数式表示：AE=　 　；DF=　 　；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．
参考答案
1．C
【解析】连接AC，BD，FH，EG，
∵四边形ABCD是矩形，
∴AC=BD，
∵E，F，G，H分别为边AB，BC，CD，DA的中点，
∴HG=AC,EF∥AC,EF=AC,EH=BD，GF=BD，
∴EH=HG =EF=GF，
∴平行四边形EFGH是菱形，
∴FH⊥EG，
∴阴影部分EFGH的面积是×HF×EG=×2×4=4，
故选C.
2．C
【解析】试题解析：整理配方式子
由非负数的性质可知：
∴四边形一定是菱形，
故选C．
3．B
【解析】AF ,∠DAC=∠BCA,∠AOF=∠COE,AC=OC,
∴.
,
四边形AECF是平行四边形，
EF⊥AC，
四边形AECF是菱形.所以选B.
4．C
【解析】解：A．正确．对角线垂直的平行四边形的菱形．
B．正确．邻边相等的平行四边形是菱形．
C．错误．对角线相等的平行四边形是矩形，不一定是菱形．
D．正确．可以证明平行四边形ABCD的邻边相等，即可判定是菱形．
故选C．
5．D
【解析】因为E，F，G，H是AB，BC，CD，DA的中点，所以EF=AD，EH∥BC且EH=BC，GF∥BC且GF=BC，所以四边形EFGH是平行四边形，当EF=EH，即AD=BC时，四边形EFGH是菱形，故选D.
6．C
【解析】试题解析：根据甲的作法作出图形，如下图所示.
∵四边形ABCD是平行四边形，
∴AD∥BC，
∵EF是AC的垂直平分线，
在和中，
∴≌，
又∵AE∥CF，
∴四边形AECF是平行四边形.
∴四边形AECF是菱形.
故甲的作法正确.
根据乙的作法作出图形，如下图所示.
∵AD∥BC，
∴∠1=∠2，∠6=∠7.
∵BF平分，AE平分
∴∠2=∠3，∠5=∠6，
∴∠1=∠3，∠5=∠7，
∵AF∥BE，且
∴四边形ABEF是平行四边形.
∵
∴平行四边形ABEF是菱形.
故乙的作法正确.
故选C.
点睛：菱形的判定方法：有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边相等的平行四边形是菱形.
7．C
【解析】图形①的两条直角边是展开图的对角线的一半，因为四边形的对角线互相平分且垂直，所以将①展开后得到的平面图形是菱形，故选C.
8．B
【解析】根据平行四边形、矩形、菱形、正方形的判定方法一一判断即可．
解：∵∠ACB=∠EFD=30°，
∴AC∥DF，
∵AC=DF，
∴四边形AFDC是平行四边形，
选项A正确；
当E是BC中点时,无法证明∠ACD=90°，
选项B错误；
B、E重合时，易证FA=FD，
∵四边形AFDC是平行四边形，
∴四边形AFDC是菱形，
选项C正确；
当四边相等时,∠AFD=60°,∠FAC=120°，
∴四边形AFDC不可能是正方形，
选项D正确.
故选B.
点睛：本题考查平行四边形、矩形、菱形、正方形的判定.熟练应用平行四边形、矩形、菱形、正方形的判定方法进行证明是解题的关键.
9．8
【解析】连接对角线交于O,如果四边形ABCD是菱形，则AC ,则AO=3，勾股定理知BO=4，BD=8.
故答案为8.
10．菱形
【解析】根据题意，DE∥AC，DF∥AB，
则四边形AEDF是平行四边形，
又∵AD是△ABC的角平分线，
∴∠EAD=∠DAF=∠ADE，
则AE=ED，
即四边形AEDF是菱形.
故答案是：菱形.
11．AC=BC
【解析】解：∵将△ABC沿BC方向平移得到△DCE，∴ACDE，∴四边形ACED为平行四边形，当AC=BC时，则DE=EC，∴平行四边形ACED是菱形．故答案为：AC=BC．
点睛：本题主要考查了平移的性质和平行四边形的判定和菱形的判定，得出ACDE是解题的关键．
12．AEDF
【解析】试题解析：∵D、E、F分别是△ABC三边的中点，
∴DE∥AC，DE=AC，EF∥AB，EF=AB，
∴四边形AEDF为平行四边形．
又∵AC=AB，
∴DE=DF．
∴四边形AEDF为菱形．
故答案为：AEDF.
13． 菱形， 矩形， 矩形， 正方形， 正方形
【解析】(1)∵ABCD是平行四边形
∴AB=DC，AD=BC
∵AB=BC
∴AB=BC=CD=DA
∴平行四边形ABCD是菱形；
(2)∵ABCD是平行四边形，AC=BD
∴平行四边形ABCD是矩形；
(3)∵ABCD是平行四边形，∠BCD=90°
∴平行四边形ABCD是矩形；
(4)∵ABCD是平行四边形，OA=OB
∴AC=BD
∴平行四边形ABCD是矩形
∵OA⊥OB
∴AC⊥BD
∴平行四边形ABCD是正方形；
(5)∵ABCD是平行四边形，AC=BD
∴平行四边形ABCD是矩形
∵AB=BC
∴平行四边形ABCD是正方形。
故答案为菱形、矩形、矩形、正方形、正方形。
14．AD=BC．
【解析】菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．据此四边形ABCD还应满足的一个条件是AD=BC．等．答案不唯一．
解：条件是AD=BC．
∵EH、GF分别是△ABC、△BCD的中位线，
∴EH∥=BC，GF∥=BC，
∴EH∥=GF，
∴四边形EFGH是平行四边形．
要使四边形EFGH是菱形，则要使AD=BC，这样，GH=AD，
∴GH=GF，
∴四边形EFGH是菱形．
15．EF⊥GH
【解析】试题分析：
如图，连接GE、GF、HF、EH，由三角形中位线定理结合AB=CD可证得EG= GF=FH=EH，由此可得四边形EHFG是菱形，从而可得EF⊥GH.
试题解析：
EF⊥GH，理由如下：
连接GE、GF、HF、EH．
∵E、G分别是AD、BD的中点，∴EG=CD，
同理FH=CD，FG=AB，EH=AB
∵AB=CD，
∴EG= GF=FH=EH，
∴平行四边形EHFG是菱形，
∴EF⊥GH.
点睛：本题的解题要点是：顺次连接题中所告诉的四个中点，这样由“三角形中位线定理”结合AB=CD即可得到GF=FH=HE=GE，从而使问题得到解决.
16．四边形ADCF是菱形，证明见解析
【解析】试题分析：根据AAS证△AFE≌△DBE，利用全等三角形的对应边相等得到AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论．
试题解析：解：四边形ADCF是菱形．理由如下：
∵AF∥BC，∴∠AFE=∠DBE．∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD．在△AFE和△DBE中，∵∠AFE=∠DBE，∠FEA=∠BED，AE=DE，∴△AFE≌△DBE（AAS），∴AF=DB．∵DB=DC，∴AF=CD．∵AF∥BC，∴四边形ADCF是平行四边形．∵∠BAC=90°，D是BC的中点，∴AD=DC=BC，∴四边形ADCF是菱形．
点睛：本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用，主要考查学生的推理能力．
17．证明见解析.
【解析】整体分析：
用SSS证△ABC≌△DCB得到EB=EC，根据“三线合一”证EF⊥BC，OB=OC，由对角线互相平分且垂直的四边形是菱形得到结论.
证明：∵AB=DC，AC=BD，BC=CB，
∴△ABC≌△DCB，
∴∠ACB=∠DBC，
∴EB=EC，
∵EF平分∠BEC，
∴EF⊥BC，BO=OC，
∵EO=OF，
∴四边形BFCE是菱形.
18．（1）见解析（2）
【解析】试题分析：（1）先证明四边形ABEC为平行四边形，再利用△ABC为等边三角形证明四边形ABEC为菱形；
（2）根据直角三角形的特征进行解答即可．
试题解析：解：（1）∵菱形ABCD，∴AB=BC，AB∥DE．∵BE∥AC，∴四边形ABEC为平行四边形．∵AB=BC，∠ABC=60°，∴△ABC为等边三角形，∴AB=AC，∴平行四边形ABEC为菱形；
（2）∵AB=6，∠ABC=60°．∵△ABC为等边三角形，∴∠OBC=30°，OB=3，∴∠OBE=30°+60°=90°，∴OE=．
19．（1）见解析；（2）菱形AFCE的周长为40cm．
【解析】试题分析： （1）由折叠可得EA=EC，FA=FC，∠2=∠3；由四边形ABCD为平行四边形可得∠1=∠2，根据等量代换可得∠1=∠3，由三线合一知△AEF为等腰三角形，所以AE=AF，从而可证四边形AFCE是菱形；
（2）由△ABF的面积为24cm2和AB=8cm，根据三角形面积公式可求出BF=6cm，利用勾股定理求出AF=10cm，从而可求出菱形的周长.
（1）证明：∵将平行四边形ABCD（AD＞AB）折叠，使点A与点C重合，
∴EF垂直平分AC，
∴EA=EC，FA=FC，
∴∠2=∠3，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠1=∠2，
∴∠1=∠3，
∵AO⊥EF，
∴△AEF为等腰三角形，
∴AE=AF，
∴AE=EC=AF=CF，
∴四边形AFCE是菱形；
（2）解：在Rt△ABF中，∵AB BF=24，AB=8cm，
∴BF=6cm，
∴AB2+BF2=AF2=100，
∴AF=10cm，
∴菱形AFCE的周长为10×4=40（cm）．
故菱形AFCE的周长为40cm．
20．（1）见解析；（2）CD=2
【解析】整体分析：
（1）用SAS证明△BAE≌△DAE，判断四边形ABED的四边都相等；（2）过点D作DF∥AE交BC于点F，判断四边形AEFD是平行四边形，△DEF是等边三角形，证明△EDC是直角三角形，用勾股定理求解.
（1）证明：如图，∵AE平分∠BAD，∴∠1=∠2，
∵AB=AD，AE=AE，
∴△BAE≌△DAE，
∴BE=DE，
∵AD∥BC，∴∠2=∠3=∠1，∴AB=BE，
∴AB=BE=DE=AD，
∴四边形ABED是菱形．
（2）解：如图，过点D作DF∥AE交BC于点F，则四边形AEFD是平行四边形，
∴DF=AE，AD=EF，
∵四边形ABED是菱形，
∴AB=BE=DE=AD，
∴DE=EF，
又∵∠ABC=60°，
∴∠DEF=60°，
∴△DEF是等边三角形，
∵CE=2DE，∴EF=FC，
∴DF=EF=FC，
∴△CDE是直角三角形．
由勾股定理求得CD=2.
21．（1）2t，2t；（2）当t=10时， AEFD是菱形；（3）当t=s或12s时，△DEF是直角三角形．
【解析】试题分析：
（1）由已知易得∠C=30°，∠DFC=90°，这样结合已知条件即可得到：DF=CD=2t，AE=2t；
（2）由（1）可知，AE=DF，结合AE∥DF可得四边形AEFD是平行四边形，由此可得当AD=AE，即60-4t=2t时，四边形AEFD是菱形，解此关于t的方程即可求得对应的t的值；
（3）如图1和图2，根据题意分∠EDF=90°和∠DEF=90°两种情况结合已知条件分析、计算即可得到对应的t的值.
试题解析：
（1）∵直角△ABC中，∠C=90°﹣∠A=30°．
∵CD=4t，AE=2t，
又∵在直角△CDF中，∠C=30°，
∴DF=CD=2t，
故答案为：2t，2t；
（2）∵DF⊥BC
∴∠CFD=90°
∵∠B=90°
∴∠B=∠CFD
∴DF∥AB，
由（1）得：DF=AE=2t，
∴四边形AEFD是平行四边形，
当AD=AE时，四边形AEFD是菱形，
即60﹣4t=2t，
解得：t=10，
即当t=10时， AEFD是菱形；
（3）分两种情况：
①当∠EDF=90°时，如图1，DE∥BC．
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t，
∴DF=2t=AE，
∴AD=4t，
∴4t=60﹣4t，
∴t=
②当∠DEF=90°时，如图2，DE⊥EF，
∵四边形AEFD是平行四边形，
∴AD∥EF，
∴DE⊥AD，
∴△ADE是直角三角形，∠ADE=90°，
∵∠A=60°，
∴∠DEA=30°，
∴AD=AE，
∴60﹣4t=t，
解得t=12．
综上所述，当t=s或12s时，△DEF是直角三角形．
版权所有@21世纪教育网(www.21cnjy.com)