浙教新版八年级下册 5.2菱形专题训练(含答案)
文档属性
| 名称 | 浙教新版八年级下册 5.2菱形专题训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-07 00:00:00 | ||
图片预览




文档简介
浙教新版八下5.2菱形专题训练
一.选择题(共15小题)(每小题2分,共30分)
1.如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
A.5 B.2 C. D.
2.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
3.菱形的周长为4,两个相邻内角度数为1:2,则该菱形的面积为( )
A. B. C.2 D.2
4.如图,已知某菱形花坛ABCD的周长是24m,∠BAD=120°,则花坛对角线AC的长是( )
A.6m B.6m C.3m D.3m
5.已知菱形的两条对角线的长分别是6和8,则菱形的周长是( )
A.36 B.30 C.24 D.20
6.如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.
A.1 B.2 C.3 D.4
7.如图,在平行四边形ABCD中,对角线AC、BD交于点O,添加下列一个条件,能使平行四边形ABCD成为菱形的是( )
A.AO=BO B.AC=AD C.AB=BC D.OD=AC
8.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣3,0),B(0,2),C(3,0),D(0,﹣2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.平行四边形
9.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD; ②AB=CD; ③OA=OC;④OB=OD; ⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是( )
A.①②④ B.③④⑤ C.①②⑤ D.①②⑥
10.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
11.如图,剪两张对边平行的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC
C.AB=CD,AD=BC D.∠DAB+∠BCD=180°
12.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
13.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
14.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )
A.10 B.12 C.16 D.18
15.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
二.填空题(共15小题)(每小题2分,共30分)
16.如图,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),对角线PM与ON交于点B,则点B的坐标为 .
17.边长为13的菱形,一条对角线长为10,则菱形的面积为 .
18.已知菱形的两条对角线长分别为1和4,则菱形的面积为 .
19.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2,则CE的长为
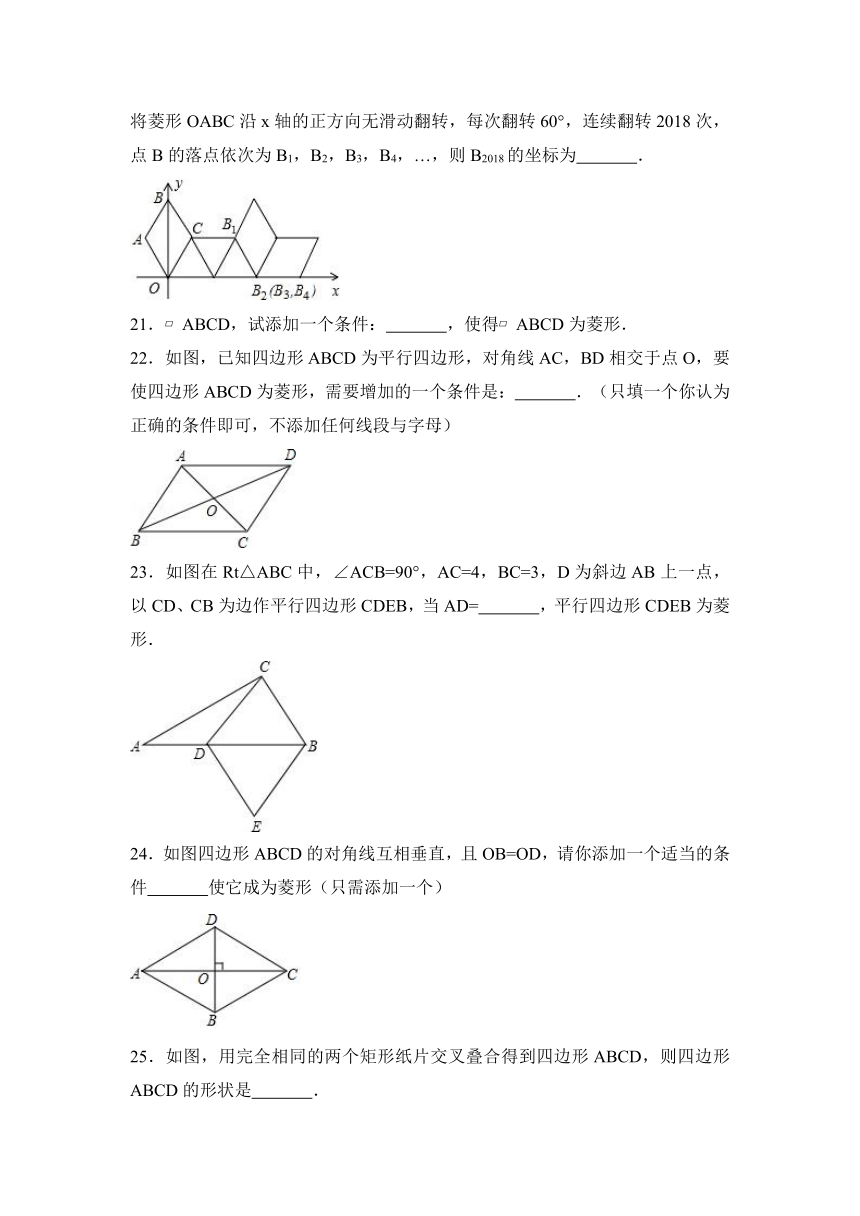
20.如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为 .
21.?ABCD,试添加一个条件: ,使得?ABCD为菱形.
22.如图,已知四边形ABCD为平行四边形,对角线AC,BD相交于点O,要使四边形ABCD为菱形,需要增加的一个条件是: .(只填一个你认为正确的条件即可,不添加任何线段与字母)
23.如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形.
24.如图四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件 使它成为菱形(只需添加一个)
25.如图,用完全相同的两个矩形纸片交叉叠合得到四边形ABCD,则四边形ABCD的形状是 .
26.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
27.如图,把两张宽度都是3cm的纸条交错的叠在一起,相交成角α.则重叠部分的面积为 .
28.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上)
①OG=AB;
②与△EGD全等的三角形共有5个;
③S四边形ODGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
29.如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则长方形纸条的宽度是 cm.
30.两个长为9,宽为3的全等矩形叠合而得到四边形ABCD(不完全重合),则四边形ABCD面积的最大值为 .
三.解答题(共8小题)(每小题5分,共40分)
31.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
32.如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值.
33.如图,在菱形中ABCD中,∠ABC=60°,点F为AD边上一点,连接BF交对角线AC于点G.
(1)如图1,已知CF⊥AD于F,菱形的边长为6,求线段FG的长度;
(2)如图2,已知点E为AB边上一点,连接CE交线段BF于点H,且满足∠FHC=60°,CH=2BH,求证:AH⊥CE.
34.如图,在△ABC中,∠ABC=90°,D,E分别为AB,AC的中点,延长DE到点F,使EF=2DE.
(1)求证:四边形BCFE是平行四边形;
(2)当∠ACB=60°时,求证:四边形BCFE是菱形.
35.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.
求证:四边形BDCE是菱形.
36.已知,如图,AD是△ABC的角平分线,DE∥AC,AF=ED.
求证:四边形AEDF是菱形.
37.如图,△ABC中,AB=AC,AD⊥BC于D,点E、F分别是AB、CD的中点.
(1)求证:四边形AEDF是菱形;
(2)如果AB=AC=BC=10,求四边形AEDF的面积S.
38.如图,在?ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB=4,AF=2DF,求CF的长.
浙教新版八下5.2菱形专题训练答案
一.选择题(共15小题)(每小题2分,共30分)
1.C.2.D.3.A.4.B.5.D.6.D.7.C.8.B.
9.A.10.D.11.D.12.A.13.B.14.C.15.A.
二.填空题(共15小题)(每小题2分,共30分)
16.(4,2).17.120.18.2.19.5或.20.(1346,0);
21.AB=BC(答案不唯一).22.AB=AD(答案不唯一).23..
24.OA=OC.25.菱形.26.6.27..28.①④.
29.2.30.15.
三.解答题(共8小题)(每小题5分,共40分)
31.(1)证明:∵四边形ABCD是菱形,
∴AO=CO,AB∥CD,
∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,
,
∴△AOE≌△COF,
∴AE=CF;
(2)∵E是AB中点,
∴BE=AE=CF.
∵BE∥CF,
∴四边形BEFC是平行四边形,
∵AB=2,
∴EF=BC=AB=2.
32.解:(1)如图1,过点P作PG⊥EF于G,
∵PE=PF,
∴FG=EG=EF=2,∠FPG=∠EPG=∠EPF,
在△FPG中,sin∠FPG===,
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,
∵四边形ABCD是菱形,
∴AD=AB,DC=BC,
∴∠DAC=∠BAC,
∴PM=PN,
在Rt△PME与Rt△PNF中,
,
∴Rt△PME≌Rt△PNF,
∴FN=EM,
在Rt△PMA中,∠PMA=90°,∠PAM=∠DAB=30°,
∴AM=AP?cos30°=3,同理AN=3,
∴AE+AF=(AM﹣EM)+(AN+NF)=6.
33.解:(1)如图1,∵四边形ABCD是菱形,
∴AD=CD,∠D=∠ABC=60°,
∴△ACD是等边三角形,
∵CF⊥AD,
∴AF=DF=3,
由勾股定理得:CF==3,
∵AD∥BC,
∴∠BCF=∠CFD=90°,
∵BC=6,
Rt△BCF中,BF==3,
∵AF∥BC,
∴=,
∴BG=2FG,
∴FG=BF=,
(2)如图2,∵∠FHC=60°,
∴∠BHC=120°,
∵AD∥BC,∠ABC=60°,
∴∠BAD=120°=∠BHC,
∠AFC=∠HBC,
∴△BHC∽△FAB,
∴,
∵CH=2BH,
∴AB=2AF,
∴F是AD的中点,
∵△ADC是等边三角形,
∴∠ACF=∠ACD=30°,
∵∠CAF=∠FHC=60°,
∴A、H、C、F四点共圆,
∴∠AHC+∠AFC=180°,
∵∠AFC=90°,
∴∠AHC=90°,
∴AH⊥CE.
34.(1)证明::∵D.E为AB,AC中点
∴DE为△ABC的中位线,DE=BC,
∴DE∥BC,
即EF∥BC,
∵EF=BC,
∴四边形BCEF为平行四边形.
(2)∵四边形BCEF为平行四边形,
∵∠ACB=60°,
∴BC=CE=BE,
∴四边形BCFE是菱形.
35.证明:∵BE∥CD,CE∥AB,
∴四边形BDCE是平行四边形.
∵∠ACB=90°,CD是AB边上的中线,
∴CD=BD,
∴平行四边形BDCE是菱形.
36.证明:∵AD是△ABC的角平分线
∴∠EAD=∠FAD
∵DE∥AC,ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形.
37.解:(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=AB=AE,
Rt△ACD中,DF=AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形;
(2)如图,
∵AB=AC=BC=10,
∴EF=5,AD=5,
∴菱形AEDF的面积S=.
38.1)证明:∵BF平分∠ABC,
∴∠ABF=∠CBF.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠AFB=∠CBF.
∴∠ABF=∠AFB.
∴AB=AF.
∵AE⊥BF,
∴∠BAO=∠FAE
∵∠FAE=∠BEO
∴∠BAO=∠BEO.
∴AB=BE.
∴AF=BE.
∴四边形ABEF是平行四边形.
∴□ABEF是菱形.
(2)解:∵AD=BC,AF=BE,
∴DF=CE.
∵AF=2DF
∴BE=2CE.
∵AB=BE=4,
∴CE=2.
过点A作AG⊥BC于点G.
∵∠ABC=60°,AB=BE,
∴△ABE是等边三角形.
∴BG=GE=2.
∴AF=CG=4.
∴四边形AGCF是平行四边形.
∴□AGCF是矩形.
∴AG=CF.
在△ABG中,∠ABC=60°,AB=4,
∴AG=.
∴CF=.
一.选择题(共15小题)(每小题2分,共30分)
1.如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
A.5 B.2 C. D.
2.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
3.菱形的周长为4,两个相邻内角度数为1:2,则该菱形的面积为( )
A. B. C.2 D.2
4.如图,已知某菱形花坛ABCD的周长是24m,∠BAD=120°,则花坛对角线AC的长是( )
A.6m B.6m C.3m D.3m
5.已知菱形的两条对角线的长分别是6和8,则菱形的周长是( )
A.36 B.30 C.24 D.20
6.如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.
A.1 B.2 C.3 D.4
7.如图,在平行四边形ABCD中,对角线AC、BD交于点O,添加下列一个条件,能使平行四边形ABCD成为菱形的是( )
A.AO=BO B.AC=AD C.AB=BC D.OD=AC
8.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣3,0),B(0,2),C(3,0),D(0,﹣2),则四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.平行四边形
9.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD; ②AB=CD; ③OA=OC;④OB=OD; ⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是( )
A.①②④ B.③④⑤ C.①②⑤ D.①②⑥
10.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
11.如图,剪两张对边平行的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC
C.AB=CD,AD=BC D.∠DAB+∠BCD=180°
12.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
13.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
14.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )
A.10 B.12 C.16 D.18
15.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
二.填空题(共15小题)(每小题2分,共30分)
16.如图,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),对角线PM与ON交于点B,则点B的坐标为 .
17.边长为13的菱形,一条对角线长为10,则菱形的面积为 .
18.已知菱形的两条对角线长分别为1和4,则菱形的面积为 .
19.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2,则CE的长为
20.如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为 .
21.?ABCD,试添加一个条件: ,使得?ABCD为菱形.
22.如图,已知四边形ABCD为平行四边形,对角线AC,BD相交于点O,要使四边形ABCD为菱形,需要增加的一个条件是: .(只填一个你认为正确的条件即可,不添加任何线段与字母)
23.如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形.
24.如图四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件 使它成为菱形(只需添加一个)
25.如图,用完全相同的两个矩形纸片交叉叠合得到四边形ABCD,则四边形ABCD的形状是 .
26.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
27.如图,把两张宽度都是3cm的纸条交错的叠在一起,相交成角α.则重叠部分的面积为 .
28.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上)
①OG=AB;
②与△EGD全等的三角形共有5个;
③S四边形ODGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
29.如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则长方形纸条的宽度是 cm.
30.两个长为9,宽为3的全等矩形叠合而得到四边形ABCD(不完全重合),则四边形ABCD面积的最大值为 .
三.解答题(共8小题)(每小题5分,共40分)
31.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
32.如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值.
33.如图,在菱形中ABCD中,∠ABC=60°,点F为AD边上一点,连接BF交对角线AC于点G.
(1)如图1,已知CF⊥AD于F,菱形的边长为6,求线段FG的长度;
(2)如图2,已知点E为AB边上一点,连接CE交线段BF于点H,且满足∠FHC=60°,CH=2BH,求证:AH⊥CE.
34.如图,在△ABC中,∠ABC=90°,D,E分别为AB,AC的中点,延长DE到点F,使EF=2DE.
(1)求证:四边形BCFE是平行四边形;
(2)当∠ACB=60°时,求证:四边形BCFE是菱形.
35.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.
求证:四边形BDCE是菱形.
36.已知,如图,AD是△ABC的角平分线,DE∥AC,AF=ED.
求证:四边形AEDF是菱形.
37.如图,△ABC中,AB=AC,AD⊥BC于D,点E、F分别是AB、CD的中点.
(1)求证:四边形AEDF是菱形;
(2)如果AB=AC=BC=10,求四边形AEDF的面积S.
38.如图,在?ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB=4,AF=2DF,求CF的长.
浙教新版八下5.2菱形专题训练答案
一.选择题(共15小题)(每小题2分,共30分)
1.C.2.D.3.A.4.B.5.D.6.D.7.C.8.B.
9.A.10.D.11.D.12.A.13.B.14.C.15.A.
二.填空题(共15小题)(每小题2分,共30分)
16.(4,2).17.120.18.2.19.5或.20.(1346,0);
21.AB=BC(答案不唯一).22.AB=AD(答案不唯一).23..
24.OA=OC.25.菱形.26.6.27..28.①④.
29.2.30.15.
三.解答题(共8小题)(每小题5分,共40分)
31.(1)证明:∵四边形ABCD是菱形,
∴AO=CO,AB∥CD,
∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,
,
∴△AOE≌△COF,
∴AE=CF;
(2)∵E是AB中点,
∴BE=AE=CF.
∵BE∥CF,
∴四边形BEFC是平行四边形,
∵AB=2,
∴EF=BC=AB=2.
32.解:(1)如图1,过点P作PG⊥EF于G,
∵PE=PF,
∴FG=EG=EF=2,∠FPG=∠EPG=∠EPF,
在△FPG中,sin∠FPG===,
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,
∵四边形ABCD是菱形,
∴AD=AB,DC=BC,
∴∠DAC=∠BAC,
∴PM=PN,
在Rt△PME与Rt△PNF中,
,
∴Rt△PME≌Rt△PNF,
∴FN=EM,
在Rt△PMA中,∠PMA=90°,∠PAM=∠DAB=30°,
∴AM=AP?cos30°=3,同理AN=3,
∴AE+AF=(AM﹣EM)+(AN+NF)=6.
33.解:(1)如图1,∵四边形ABCD是菱形,
∴AD=CD,∠D=∠ABC=60°,
∴△ACD是等边三角形,
∵CF⊥AD,
∴AF=DF=3,
由勾股定理得:CF==3,
∵AD∥BC,
∴∠BCF=∠CFD=90°,
∵BC=6,
Rt△BCF中,BF==3,
∵AF∥BC,
∴=,
∴BG=2FG,
∴FG=BF=,
(2)如图2,∵∠FHC=60°,
∴∠BHC=120°,
∵AD∥BC,∠ABC=60°,
∴∠BAD=120°=∠BHC,
∠AFC=∠HBC,
∴△BHC∽△FAB,
∴,
∵CH=2BH,
∴AB=2AF,
∴F是AD的中点,
∵△ADC是等边三角形,
∴∠ACF=∠ACD=30°,
∵∠CAF=∠FHC=60°,
∴A、H、C、F四点共圆,
∴∠AHC+∠AFC=180°,
∵∠AFC=90°,
∴∠AHC=90°,
∴AH⊥CE.
34.(1)证明::∵D.E为AB,AC中点
∴DE为△ABC的中位线,DE=BC,
∴DE∥BC,
即EF∥BC,
∵EF=BC,
∴四边形BCEF为平行四边形.
(2)∵四边形BCEF为平行四边形,
∵∠ACB=60°,
∴BC=CE=BE,
∴四边形BCFE是菱形.
35.证明:∵BE∥CD,CE∥AB,
∴四边形BDCE是平行四边形.
∵∠ACB=90°,CD是AB边上的中线,
∴CD=BD,
∴平行四边形BDCE是菱形.
36.证明:∵AD是△ABC的角平分线
∴∠EAD=∠FAD
∵DE∥AC,ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形.
37.解:(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=AB=AE,
Rt△ACD中,DF=AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形;
(2)如图,
∵AB=AC=BC=10,
∴EF=5,AD=5,
∴菱形AEDF的面积S=.
38.1)证明:∵BF平分∠ABC,
∴∠ABF=∠CBF.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠AFB=∠CBF.
∴∠ABF=∠AFB.
∴AB=AF.
∵AE⊥BF,
∴∠BAO=∠FAE
∵∠FAE=∠BEO
∴∠BAO=∠BEO.
∴AB=BE.
∴AF=BE.
∴四边形ABEF是平行四边形.
∴□ABEF是菱形.
(2)解:∵AD=BC,AF=BE,
∴DF=CE.
∵AF=2DF
∴BE=2CE.
∵AB=BE=4,
∴CE=2.
过点A作AG⊥BC于点G.
∵∠ABC=60°,AB=BE,
∴△ABE是等边三角形.
∴BG=GE=2.
∴AF=CG=4.
∴四边形AGCF是平行四边形.
∴□AGCF是矩形.
∴AG=CF.
在△ABG中,∠ABC=60°,AB=4,
∴AG=.
∴CF=.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
