6.2反比例函数的图象及性质(1)课件

课件13张PPT。 6.2 反比例函数的图象及性质(1)义务教育课程标准实验教科　
浙江版《数学》九年级上册1.一次函数y=kx+b(k≠0)的图象是 。在直角坐标系中作一次函数的图象时，只要确
定 个点，再过这 个点画直线．一条直线两两2.反比例函数的图象又会是什么样子呢?如何
画反比例函数的图像呢？作函数图象的方法是 ， 描点法描点法步骤是 、 、 。列表 描点 连线123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………用描点法画出反比例函数 的图像。合作学习：（1）列表：根据下表x的取值，求出对应的y的值。（3）连线：（2）描点：以表中各组对应值为点的坐标，在直角坐标系中描出相应的点；按自变量从小到大的顺序,将点用光滑曲线连接。123456-1-3-2-4-51234-1-2-3-40-6-556yx16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……用描点法画出反比例函数 的图像。试一试：123456-1-3-2-4-5-61234-1-2-3-40-6-556xy 反比例函数图象画法步骤：列
表描
点连
线 描点法注意：①列x与y的对应值表时，x的值不能为零，但仍可以零的基础，左右
均匀、对称地取值。注意：②描点时自左住右用光滑曲线顺次连结，切忌用折线。注意： ③两个分支合起来才是反比例函数图象。 讨 论反比例函数图像的性质①图像的形状。
②当k>0时，双曲线两分支各在哪些象限？
当k<0?
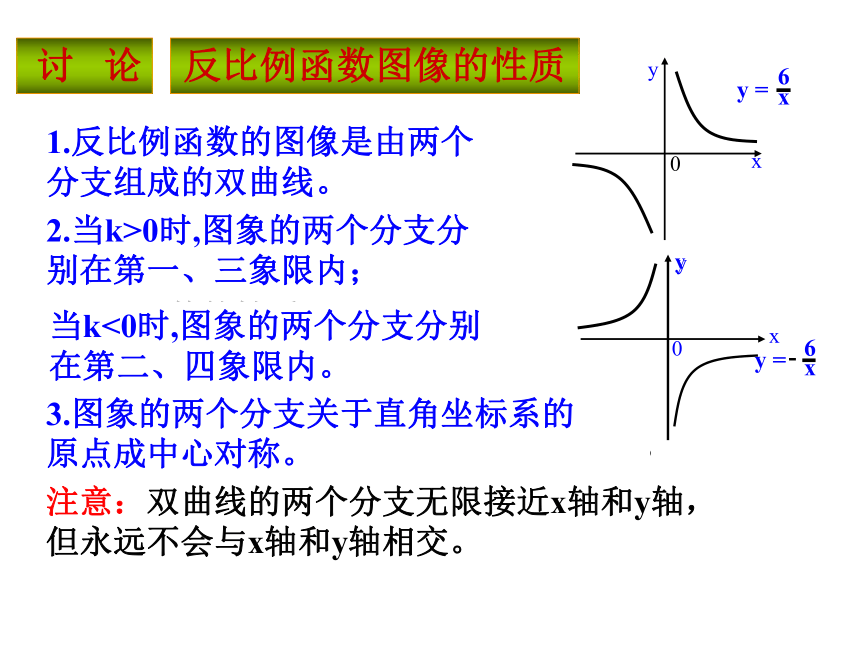
③图像还有哪些特点？2.当k>0时,图象的两个分支分别在第一、三象限内；当k<0时,图象的两个分支分别在第二、四象限内。注意：双曲线的两个分支无限接近x轴和y轴，但永远不会与x轴和y轴相交。
1.反比例函数的图像是由两个 分支组成的双曲线。3.图象的两个分支关于直角坐标系的 原点成中心对称。已知反比例函数y=k/x(k≠0）的图象的一支如图所示，它经过点B(-4,2)。
（1）判断k是正数还是负数；
（2）求这个反比例函数的解析式；
（3）补画这个反比例函数图象的另一支。例 1xy0（-4，2）1.函数 的图象在第_____象限，
2. 双曲线 经过点（-3，___）3.函数 的图象在二、四象限，则m的
取值范围是 ____ .
4.对于函数 ，当 x<0时，对应的图象
分布在第______象限. 练习 1二,四m < 2三
5、已知反比例函数 （k≠0） 的图象上
一点的坐标为（ ，2 ）。
求这个反比例函数的解析式。6. 已知k<0,则函数 y1=kx , y2= 在同一坐标系中的图象大致是 ( )D位置位置y=kx ( k≠0 ) 直线 双曲线一三象限一三象限二四象限二四象限
填表分析正比例函数和反比例函数的区别小结：拓展提高反比例函数y= (k>0)在第一象限内的图像
如图所示,P为该图像上任意一点,PQ⊥x轴于Q,
设△POQ的面积为S,则S与k之间的关系是( ) 如图P是反比例函数y= 上一点,若图中阴影部分
的矩形面积是2,求这个反比例函数的解析式。拓展提高