6.2 反比例函数的图象和性质(1)同步练习
文档属性
| 名称 | 6.2 反比例函数的图象和性质(1)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-12 16:23:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
6.2 反比例函数的图象和性质(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1. 反比例函数y=(k≠0)的图象是双曲线
用描点法画反比例函数的图象,步骤:列表- ( http: / / www.21cnjy.com )--描点---连线.
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值.
(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确.
(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线.
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.21教育网
2. 反比例函数y=(k≠0),当k>0,双曲线的两支分别位于第一、第三象限 ;当k<0,双曲线的两支分别位于第二、第四象限21教育名师原创作品
3. 反比例函数图象既是轴对称图形又是中心 ( http: / / www.21cnjy.com )对称图形,对称轴分别是:①二、四象限的角平分线Y=-X;②一、三象限的角平分线Y=X;对称中心是:坐标原点.
基础知识和能力拓展精练
一、选择题
1.下列函数的图象位于第一、第三象限的是( )
A. y=﹣x2 B. y=x2 C. y= EMBED Equation.DSMT4 D. y=﹣
2.当时,反比例函数的图象在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.若反比例函数y=的图象经过点(m,3m),其中m≠0,则反比例函数的图象在( )
A. 第一、二象限 B. 第一、三象限 C. 第二、四象限 D. 一、三或二、四象限
4.如图,过反比例函数的图象上一点作轴于点,连接.若,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
5.在同一直角坐标系中,函数y=-kx+k与y= (k≠0)的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.为了更好保护水资源,造福人类.某工厂计 ( http: / / www.21cnjy.com )划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
7.已知反比例函数的图象在第二、四象限内,则m的值是( )
A. 2 B. -2 C. 土2 D.
8.反比例函数的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
( http: / / www.21cnjy.com )
A. ①② B. ②③ C. ③④ D. ①④
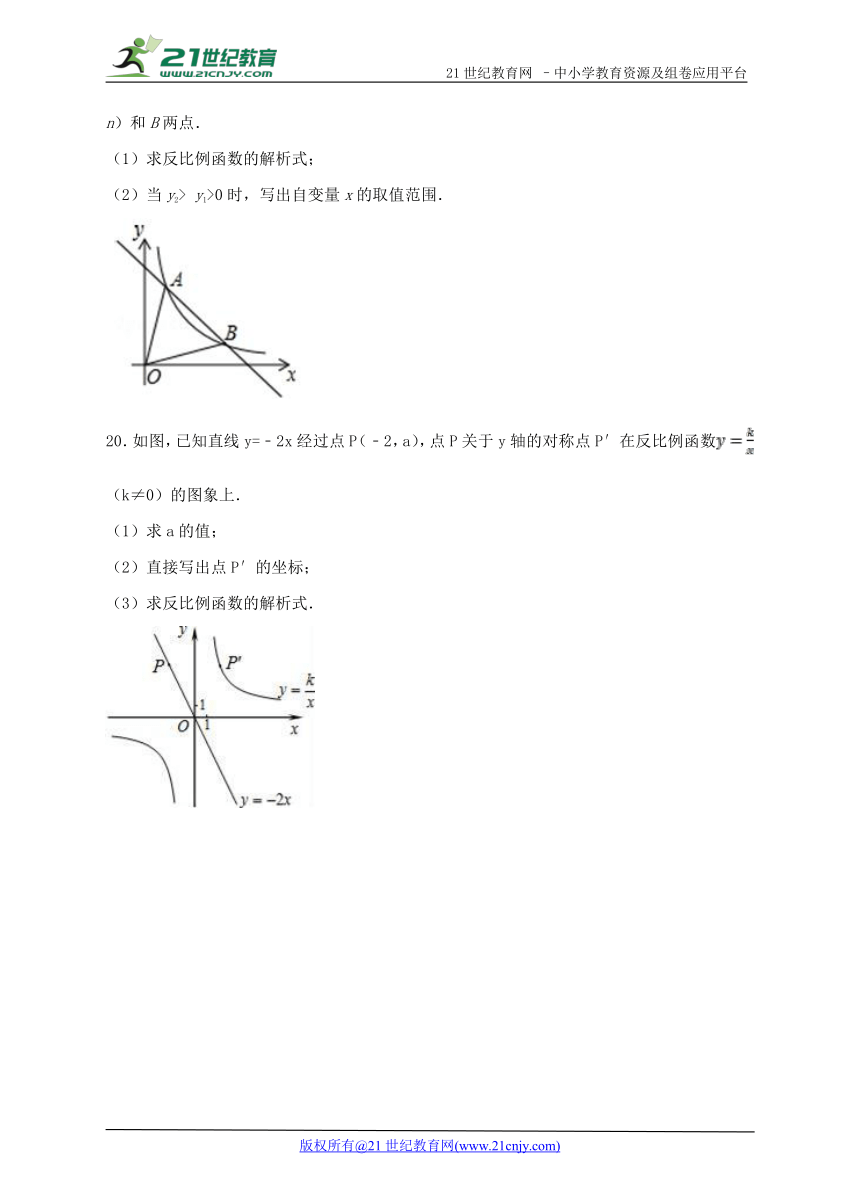
9.如图,已知在中,点A(1,2),∠OBA=90 ,OB在x轴上.将△AOB绕点A逆时针旋转90 ,点O的对应点C恰好落在双曲线上,则的值为( ).
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
二、填空题
10.已知反比例函数的图象经过点 和 ,则 的值是_______.
11.已知三角形的面积一定,则它的底边a上的高h与底边a之间的函数关系的图象大致是________.(将满足条件的序号填入横线上)2·1·c·n·j·y
( http: / / www.21cnjy.com )
(1) (2) (3) (4)21*cnjy*com
12.关于的反比例函数(为常数)的图像在第一、三象限,则的值为____________;
13.在平面直角坐标系中,O是坐标原点.点P(m,n)在反比例函数的图象上.若m=k,n=k-2,则点P的坐标为________;
14.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′称为点P的“倒影点”.直线y=-x+1上有两点A,B,它们的“倒影点”A′,B′均在反比例函数y=的图象上.若AB=2,则k=________.
三、解答题
15.画反比例函数的图象,并指出:
(l)x取什么值时反比例函数的值是正数?
(2)点(0, 0),(0.01,-400)是图象上的点吗?
16.已知函数y=的图象经过点(-3,4).
(1)求k的值,并在正方形网格中画出这个函数的图象;
(2)当x取什么值时,函数的值小于0
( http: / / www.21cnjy.com )
17.已知正比例函数y=kx与比例函数的图象都过点A(m,1).求:
(1)正比例函数的表达式;
(2)正比例函数图象与反比例数图象的另一个交点的坐标.
18.已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)k的值为______ ;
(2)判断点B(-1,6)是否在这个函数的图象上,并说明理由;
(3)当x<3时,直接写出y的取值范围.
19.如图,一次函数y1=﹣x+5的图象与反比例函数y2=(k≠0)在第一象限的图象交于A(1,n)和B两点.21世纪教育网版权所有
(1)求反比例函数的解析式;
(2)当y2> y1>0时,写出自变量x的取值范围.
( http: / / www.21cnjy.com )
20.如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数(k≠0)的图象上.www-2-1-cnjy-com
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
( http: / / www.21cnjy.com )
参考答案
1.C
【解析】选项A,图象过三,四象限,
选项B,图象过一,二象限,
选项C,图象过一,三象限,
选项D,图象过二,四象限.
故选C.
2.C
【解析】k>0,反比例函数图像位于第一、三象限,
∵x<0,∴反比例函数图像位于第三象限.
故选C.
点睛:反比例函数y=(k≠0),若k>0,那么反比例函数图像位于第一、三象限;若k<0,那么反比例函数图像位于第二、四象限.21cnjy.com
3.B
【解析】试题解析:将(m,3m)代入y=得,
3m=
k=3m2>0,
因此反比例函数的图象在一,三象限.
故选B.
点睛:反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数,同时要熟悉反比例函数的性质.21·cn·jy·com
4.C
【解析】试题解析:∵点A是反比例函数y=图象上一点,且AB⊥x轴于点B,
∴S△AOB=|k|=2,
解得:k=±4.
∵反比例函数在第一象限有图象,
∴k=4.
故选C.
【点睛】本题考查了反比例函 ( http: / / www.21cnjy.com )数的性质以及反比例函数系数k的几何意义,解题的关键是找出关于k的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义找出关于k的含绝对值符号的一元一次方程是关键.
5.C
【解析】当k>0时,函数y=-kx+k的图象分布在第一、二、四象限,函数y= 的图象位于第一、三象限。www.21-cn-jy.com
故本题正确答案为C.
6.C
【解析】因为v=sh,所以,其中v是常量,h>0,所以函数图象是在第一象限的双曲线的一条分支,故选C.21·世纪*教育网
7.B
【解析】∵反比例函数的图象在第二、四象限内,
∴ ,解得:.
故选B.
点睛:若函数是关于的反比例函数,且图象在第二、四象限,则需同时满足两个条件:(1);(2).【来源:21·世纪·教育·网】
8.C
【解析】∵反比例函数的图象位于一三象限,
∴m>0
故①错误;
当反比例函数的图象位于一三象限时,在每一象限内,y随x的增大而减小,故②错误;
将A(﹣1,h),B(2,k)代入得到h=﹣m,2k=m,
∵m>0
∴h<k
故③正确;
将P(x,y)代入得到m=xy,将P′(﹣x,﹣y)代入得到m=xy,
故P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上
故④正确,
故选:C.
9.C
【解析】分析:由坐标与图形旋转求出点C坐标,再利用反比例整数解析式求k
OB=CD=1.AB=2.一定要把C点坐标求对.
坐标与图形的旋转是关键.
本题解析: 由A(1,2)可知OB=1,AB=2.将△AOB绕点A逆时针旋转90°得到△ACD,则△AOB △ACD,所以CD=OB=1,AD=AB=2.所以点C坐标(3,1),又点C在双曲线 y= (x>0)上,∴1= ,k=3.2-1-c-n-j-y
故答案为:C.
10.-6
【解析】∵反比例函数的图象过点(3,2)和点(t,1),
∴t×(-1)=3×2,即t=-6.
故答案为:-6.
点睛:若两个点A(a,b)和点B(m,n)都在同一反比例函数的图象上,则.
11.(4)
【解析】设面积为k,则2k=ah,所以,又因为a>0,所以图象是反比例函数在第一象限的部分,故答案为(4).【出处:21教育名师】
12.2;
【解析】试题解析:根据题意得:k2-5=-1
解得:k=±2
∵函数图像在第一、三象限
∴k>0
即k=2.
13.(3,1)
【解析】∵把m=k,n=k-2代入反比例函数y= 中,得k-2=1,解得k=3,
∴m=3,n=3-2=1,
∴点P的坐标为(3,1).
故答案为(3,1).【版权所有:21教育】
点睛:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上点的坐标一定适合反比例函数的解析式.21*cnjy*com
14.-
【解析】试题解析:设点A(a,﹣a+1),B(b,﹣b+1)(a<b),则A′(,),B′(,),
∵AB=,
∴b﹣a=2,即b=a+2.
∵点A′,B′均在反比例函数的图象上,
∴,解得:k=.
故答案为:.
15.(1)x<0(2)不是
【解析】试题分析:(1)画出图象,由图象直接得出结论即可;
(2)由图象可知,显然不过原点(0,0),把另一个点的横坐标代入解析式,比较纵坐标的值即可得出结论.
试题解析:解:(1)图象如图,由图象可知:当x<0时,y>0;
( http: / / www.21cnjy.com )
(2)由图象可知,图象不过原点,∴(0,0)不是图象上的点;
当x=0.01时, ,∴(0.01,-400)不是图象上的点.
16.(1) ;图象见解析;(2)x>0.
【解析】试题分析:(1)把点(-3,4)代入反比例函数解析式可得k的值;
(2)看x轴下方的函数图象所对应的自变量的取值即可.
试题解析:(1)把(-3,4)代入y=,得k=-3×4=-12,
∴y=-,
( http: / / www.21cnjy.com )
(2)由图象可以看出,当x>0时,函数的值小于0.
点睛:反比例函数的比例系数等于反比例函数上的点的横纵坐标的积;函数值小于0,求自变量取值,看x轴下方的函数图象所对应的自变量取值即可.
17.(-3,-1)
【解析】把A的坐标分别代入函数的表达式求解,解由它们组成的方程组即可得解.
解:(1)因为y=kx与都过点A(m,1)所以解得所以正正函数表达式为 (2)由得所以它们的另一个交点坐标为(-3,-1).
18.(1)6 ;(2)不在;(3)y>2或y<0.
【解析】试题分析:(1)将A(2,3)代入y=中可以求出k的值;(2)将x=-1代入反比例函数解析式,若函数值等于6,那么点在这个函数的图像上,若函数值不等于6,那么这个点不在这个函数图像上;(3)画出函数图像,根据图像直接写出y的范围.
试题解析:
(1)∵A(2,3),∴k=6;
(2)B(-1,6)不在这个函数的图象上,
∵反比例函数解析式为:y=,令x=-1,y=-6≠6,
∴B(-1,6)不在这个函数的图象上;
(3)当x=3时,y=2,
如图,点A(3,2),
( http: / / www.21cnjy.com )
当x<3时,y>2或y<0.
点睛:本题关键掌握反比例函数的图像和性质.
19.(1)y=;(2)4<x<5或0<x<1
【解析】试题分析:(1)将点A 的横坐标代入直线的解析式求出点A的坐标,然后将的A的坐标代入反比例函数的解析式即可.
(2)当y2>y1>0时,双曲线便在直线的上方且在x轴的上方,所以求出直线与双曲线及x轴的交点后可由图象直接写出其对应的x取值范围.
试题解析:(1)∵点A(1,n)在一次函数y1=-x+5的图象上,
∴当x=1时,y=-1+5=4
即:A点的坐标为:(1,4)
∵点A(1,4)在反比例函数y2=(k≠0)的图象上
∴k=1×4=4
∴反比例函数的解析式为:y2=
(2)如下图所示:
解方程组:得或
∴B点的坐标为(4,1)
直线与x轴的交点C为(5,0)
( http: / / www.21cnjy.com )
由图象可知:当 4<x<5或0<x<1时,y2>y1>0.
20.(1)4;(2)P′(2,4);(3)
【解析】试题分析:(1)把(-2,a)代入y=-2x中即可求a;
(2)坐标系中任一点关于y轴对称的点的坐标,其中横坐标等于原来点横坐标的相反数,纵坐标不变;
(3)把P′代入y=中,求出k,即可得出反比例函数的解析式.
试题解析:(1)把(-2,a)代入y=-2x中,得a=-2×(-2)=4,
∴a=4;
(2)∵P点的坐标是(-2,4),
∴点P关于y轴的对称点P′的坐标是(2,4);
(3)把P′(2,4)代入函数式y=,得
,
∴k=8,
∴反比例函数的解析式是y=.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
6.2 反比例函数的图象和性质(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1. 反比例函数y=(k≠0)的图象是双曲线
用描点法画反比例函数的图象,步骤:列表- ( http: / / www.21cnjy.com )--描点---连线.
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值.
(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确.
(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线.
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.21教育网
2. 反比例函数y=(k≠0),当k>0,双曲线的两支分别位于第一、第三象限 ;当k<0,双曲线的两支分别位于第二、第四象限21教育名师原创作品
3. 反比例函数图象既是轴对称图形又是中心 ( http: / / www.21cnjy.com )对称图形,对称轴分别是:①二、四象限的角平分线Y=-X;②一、三象限的角平分线Y=X;对称中心是:坐标原点.
基础知识和能力拓展精练
一、选择题
1.下列函数的图象位于第一、第三象限的是( )
A. y=﹣x2 B. y=x2 C. y= EMBED Equation.DSMT4 D. y=﹣
2.当时,反比例函数的图象在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.若反比例函数y=的图象经过点(m,3m),其中m≠0,则反比例函数的图象在( )
A. 第一、二象限 B. 第一、三象限 C. 第二、四象限 D. 一、三或二、四象限
4.如图,过反比例函数的图象上一点作轴于点,连接.若,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
5.在同一直角坐标系中,函数y=-kx+k与y= (k≠0)的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.为了更好保护水资源,造福人类.某工厂计 ( http: / / www.21cnjy.com )划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
7.已知反比例函数的图象在第二、四象限内,则m的值是( )
A. 2 B. -2 C. 土2 D.
8.反比例函数的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
( http: / / www.21cnjy.com )
A. ①② B. ②③ C. ③④ D. ①④
9.如图,已知在中,点A(1,2),∠OBA=90 ,OB在x轴上.将△AOB绕点A逆时针旋转90 ,点O的对应点C恰好落在双曲线上,则的值为( ).
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
二、填空题
10.已知反比例函数的图象经过点 和 ,则 的值是_______.
11.已知三角形的面积一定,则它的底边a上的高h与底边a之间的函数关系的图象大致是________.(将满足条件的序号填入横线上)2·1·c·n·j·y
( http: / / www.21cnjy.com )
(1) (2) (3) (4)21*cnjy*com
12.关于的反比例函数(为常数)的图像在第一、三象限,则的值为____________;
13.在平面直角坐标系中,O是坐标原点.点P(m,n)在反比例函数的图象上.若m=k,n=k-2,则点P的坐标为________;
14.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′称为点P的“倒影点”.直线y=-x+1上有两点A,B,它们的“倒影点”A′,B′均在反比例函数y=的图象上.若AB=2,则k=________.
三、解答题
15.画反比例函数的图象,并指出:
(l)x取什么值时反比例函数的值是正数?
(2)点(0, 0),(0.01,-400)是图象上的点吗?
16.已知函数y=的图象经过点(-3,4).
(1)求k的值,并在正方形网格中画出这个函数的图象;
(2)当x取什么值时,函数的值小于0
( http: / / www.21cnjy.com )
17.已知正比例函数y=kx与比例函数的图象都过点A(m,1).求:
(1)正比例函数的表达式;
(2)正比例函数图象与反比例数图象的另一个交点的坐标.
18.已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)k的值为______ ;
(2)判断点B(-1,6)是否在这个函数的图象上,并说明理由;
(3)当x<3时,直接写出y的取值范围.
19.如图,一次函数y1=﹣x+5的图象与反比例函数y2=(k≠0)在第一象限的图象交于A(1,n)和B两点.21世纪教育网版权所有
(1)求反比例函数的解析式;
(2)当y2> y1>0时,写出自变量x的取值范围.
( http: / / www.21cnjy.com )
20.如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数(k≠0)的图象上.www-2-1-cnjy-com
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
( http: / / www.21cnjy.com )
参考答案
1.C
【解析】选项A,图象过三,四象限,
选项B,图象过一,二象限,
选项C,图象过一,三象限,
选项D,图象过二,四象限.
故选C.
2.C
【解析】k>0,反比例函数图像位于第一、三象限,
∵x<0,∴反比例函数图像位于第三象限.
故选C.
点睛:反比例函数y=(k≠0),若k>0,那么反比例函数图像位于第一、三象限;若k<0,那么反比例函数图像位于第二、四象限.21cnjy.com
3.B
【解析】试题解析:将(m,3m)代入y=得,
3m=
k=3m2>0,
因此反比例函数的图象在一,三象限.
故选B.
点睛:反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数,同时要熟悉反比例函数的性质.21·cn·jy·com
4.C
【解析】试题解析:∵点A是反比例函数y=图象上一点,且AB⊥x轴于点B,
∴S△AOB=|k|=2,
解得:k=±4.
∵反比例函数在第一象限有图象,
∴k=4.
故选C.
【点睛】本题考查了反比例函 ( http: / / www.21cnjy.com )数的性质以及反比例函数系数k的几何意义,解题的关键是找出关于k的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义找出关于k的含绝对值符号的一元一次方程是关键.
5.C
【解析】当k>0时,函数y=-kx+k的图象分布在第一、二、四象限,函数y= 的图象位于第一、三象限。www.21-cn-jy.com
故本题正确答案为C.
6.C
【解析】因为v=sh,所以,其中v是常量,h>0,所以函数图象是在第一象限的双曲线的一条分支,故选C.21·世纪*教育网
7.B
【解析】∵反比例函数的图象在第二、四象限内,
∴ ,解得:.
故选B.
点睛:若函数是关于的反比例函数,且图象在第二、四象限,则需同时满足两个条件:(1);(2).【来源:21·世纪·教育·网】
8.C
【解析】∵反比例函数的图象位于一三象限,
∴m>0
故①错误;
当反比例函数的图象位于一三象限时,在每一象限内,y随x的增大而减小,故②错误;
将A(﹣1,h),B(2,k)代入得到h=﹣m,2k=m,
∵m>0
∴h<k
故③正确;
将P(x,y)代入得到m=xy,将P′(﹣x,﹣y)代入得到m=xy,
故P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上
故④正确,
故选:C.
9.C
【解析】分析:由坐标与图形旋转求出点C坐标,再利用反比例整数解析式求k
OB=CD=1.AB=2.一定要把C点坐标求对.
坐标与图形的旋转是关键.
本题解析: 由A(1,2)可知OB=1,AB=2.将△AOB绕点A逆时针旋转90°得到△ACD,则△AOB △ACD,所以CD=OB=1,AD=AB=2.所以点C坐标(3,1),又点C在双曲线 y= (x>0)上,∴1= ,k=3.2-1-c-n-j-y
故答案为:C.
10.-6
【解析】∵反比例函数的图象过点(3,2)和点(t,1),
∴t×(-1)=3×2,即t=-6.
故答案为:-6.
点睛:若两个点A(a,b)和点B(m,n)都在同一反比例函数的图象上,则.
11.(4)
【解析】设面积为k,则2k=ah,所以,又因为a>0,所以图象是反比例函数在第一象限的部分,故答案为(4).【出处:21教育名师】
12.2;
【解析】试题解析:根据题意得:k2-5=-1
解得:k=±2
∵函数图像在第一、三象限
∴k>0
即k=2.
13.(3,1)
【解析】∵把m=k,n=k-2代入反比例函数y= 中,得k-2=1,解得k=3,
∴m=3,n=3-2=1,
∴点P的坐标为(3,1).
故答案为(3,1).【版权所有:21教育】
点睛:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上点的坐标一定适合反比例函数的解析式.21*cnjy*com
14.-
【解析】试题解析:设点A(a,﹣a+1),B(b,﹣b+1)(a<b),则A′(,),B′(,),
∵AB=,
∴b﹣a=2,即b=a+2.
∵点A′,B′均在反比例函数的图象上,
∴,解得:k=.
故答案为:.
15.(1)x<0(2)不是
【解析】试题分析:(1)画出图象,由图象直接得出结论即可;
(2)由图象可知,显然不过原点(0,0),把另一个点的横坐标代入解析式,比较纵坐标的值即可得出结论.
试题解析:解:(1)图象如图,由图象可知:当x<0时,y>0;
( http: / / www.21cnjy.com )
(2)由图象可知,图象不过原点,∴(0,0)不是图象上的点;
当x=0.01时, ,∴(0.01,-400)不是图象上的点.
16.(1) ;图象见解析;(2)x>0.
【解析】试题分析:(1)把点(-3,4)代入反比例函数解析式可得k的值;
(2)看x轴下方的函数图象所对应的自变量的取值即可.
试题解析:(1)把(-3,4)代入y=,得k=-3×4=-12,
∴y=-,
( http: / / www.21cnjy.com )
(2)由图象可以看出,当x>0时,函数的值小于0.
点睛:反比例函数的比例系数等于反比例函数上的点的横纵坐标的积;函数值小于0,求自变量取值,看x轴下方的函数图象所对应的自变量取值即可.
17.(-3,-1)
【解析】把A的坐标分别代入函数的表达式求解,解由它们组成的方程组即可得解.
解:(1)因为y=kx与都过点A(m,1)所以解得所以正正函数表达式为 (2)由得所以它们的另一个交点坐标为(-3,-1).
18.(1)6 ;(2)不在;(3)y>2或y<0.
【解析】试题分析:(1)将A(2,3)代入y=中可以求出k的值;(2)将x=-1代入反比例函数解析式,若函数值等于6,那么点在这个函数的图像上,若函数值不等于6,那么这个点不在这个函数图像上;(3)画出函数图像,根据图像直接写出y的范围.
试题解析:
(1)∵A(2,3),∴k=6;
(2)B(-1,6)不在这个函数的图象上,
∵反比例函数解析式为:y=,令x=-1,y=-6≠6,
∴B(-1,6)不在这个函数的图象上;
(3)当x=3时,y=2,
如图,点A(3,2),
( http: / / www.21cnjy.com )
当x<3时,y>2或y<0.
点睛:本题关键掌握反比例函数的图像和性质.
19.(1)y=;(2)4<x<5或0<x<1
【解析】试题分析:(1)将点A 的横坐标代入直线的解析式求出点A的坐标,然后将的A的坐标代入反比例函数的解析式即可.
(2)当y2>y1>0时,双曲线便在直线的上方且在x轴的上方,所以求出直线与双曲线及x轴的交点后可由图象直接写出其对应的x取值范围.
试题解析:(1)∵点A(1,n)在一次函数y1=-x+5的图象上,
∴当x=1时,y=-1+5=4
即:A点的坐标为:(1,4)
∵点A(1,4)在反比例函数y2=(k≠0)的图象上
∴k=1×4=4
∴反比例函数的解析式为:y2=
(2)如下图所示:
解方程组:得或
∴B点的坐标为(4,1)
直线与x轴的交点C为(5,0)
( http: / / www.21cnjy.com )
由图象可知:当 4<x<5或0<x<1时,y2>y1>0.
20.(1)4;(2)P′(2,4);(3)
【解析】试题分析:(1)把(-2,a)代入y=-2x中即可求a;
(2)坐标系中任一点关于y轴对称的点的坐标,其中横坐标等于原来点横坐标的相反数,纵坐标不变;
(3)把P′代入y=中,求出k,即可得出反比例函数的解析式.
试题解析:(1)把(-2,a)代入y=-2x中,得a=-2×(-2)=4,
∴a=4;
(2)∵P点的坐标是(-2,4),
∴点P关于y轴的对称点P′的坐标是(2,4);
(3)把P′(2,4)代入函数式y=,得
,
∴k=8,
∴反比例函数的解析式是y=.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
