3.8 正多边形和圆、弧长公式及有关计算 学案(无答案)
文档属性
| 名称 | 3.8 正多边形和圆、弧长公式及有关计算 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-13 00:00:00 | ||
图片预览




文档简介
数学备课组
教师
班级
学生
日期:
上课时间:
主课题:正多边形和圆、弧长公式及有关计算
教学目标:
1. 正多边形的有关概念;正多边形、正多边形的中心、半径、边心距、中心角。正n边形的半径,边心距把正n边形分成2n个全等的直角三角形。
2. 正多边形和圆的关系定理
教学重难点:
1、正多边形和圆关系,弧长公式及应用。
2、正多边形的计算可转化为解直角三角形的问题。
3、解决有关正多边形和圆的计算,应用弧长公式。
教学内容
【同步检测】
1、 正六边形两条对边之间的距离是2,则它的边长是( )
A. B. C. D.
2、如图,两相交圆的公共弦AB为,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比。
【知识精讲】
、重点梳理
、经典例题
例1、如图,扇形OAB的圆心角为,分别以OA、OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( ) A.P=Q B.P>Q C.Q>P D.无法确定
变式训练:如图,△ABC中,,,,分别以AC、BC为直径作半圆,则图中阴影的面积为( ) A. B. C. D.
例2、如图,与相切于点,与轴交于,两点,且、是一元二次方程的两个实数根,求的半径及图中阴影部分的面积.
变式训练:如图,的半径为1,正方形ABCD顶点B坐标为(5,0),顶点D在上运动. ①当点D运动到与点A、O在同一条直线上时,试证明直线CD与 相切; ②当直线CD与相切时,求CD所在直线对应的函数关系式; ③设点D的横坐标为,正方形ABCD的面积为S,求S与之间的函数关系式,并求出S的最大值与最小值.
例3、在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,求S3﹣S4的值。
例4、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)△ADF∽△AED;
(2)FG=2;
(3)S△DEF=4.
变式训练:如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°,求证:;
(2)如图②,若,求的值.
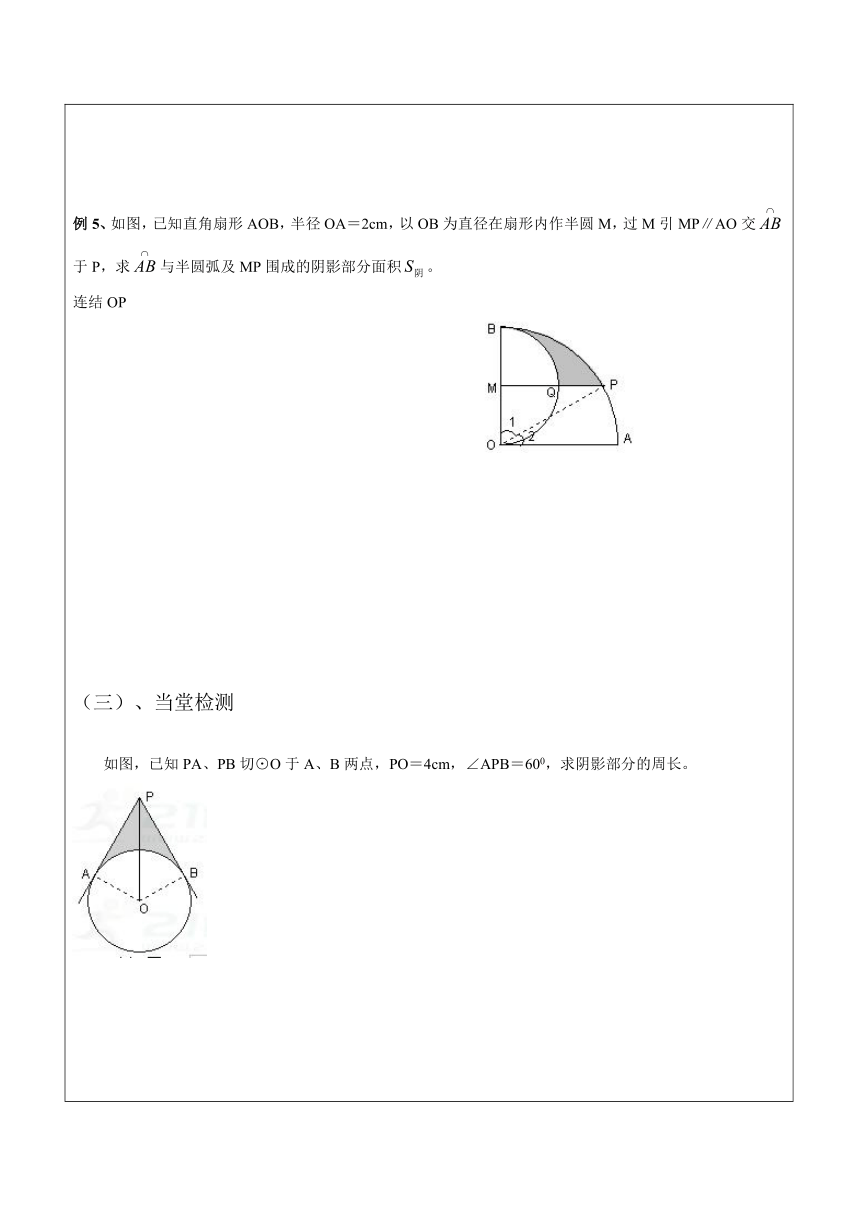
例5、如图,已知直角扇形AOB,半径OA=2cm,以OB为直径在扇形内作半圆M,过M引MP∥AO交于P,求与半圆弧及MP围成的阴影部分面积。
连结OP
(三)、当堂检测
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=600,求阴影部分的周长。
【提高训练】
如图,大小两个同心圆的圆心为O,现任作小圆的三条切线分别交于A、B、C点,记△ABC的面积为,以A、B、C为顶点的三个阴影部分的面积分别为、、,试判断是否为定值,若是,求出这个定值;若不是,请说明理由。
2、如图,⊙O与⊙外切于M,AB、CD是它们的外公切线,A、B、C、D为切点,⊥OA于E,且∠AOC=1200。
(1)求证:⊙的周长等于的弧长;
(2)若⊙的半径为1cm,求图中阴影部分的面积。
【课后练习】
一、选择题:
1、正六边形的两条平行边之间的距离为1,则它的边长为( )
A、 B、 C、 D、
2、如图,两同心圆间的圆环的面积为,过小圆上任一点P作大圆的弦AB,则 的值是( )
A、16 B、 C、4 D、
3、如图,AB为半圆O的直径,C为半圆上一点,且为半圆的,设扇形AOC、△COB、弓形BC的面积分别为、、,则下列结论正确的是( )
A、<< B、<<
C、<< D、<<
4、如图,⊙O1和⊙O2外切于P,它们的外公切线与两圆分别相切于点A、B,设⊙O1的半径为,⊙O2的半径为,的长为,的长为,若,则( )
A、 B、 C、 D、
5、如图,A是半径为1的⊙O外一点,OA=2,AB切⊙O于B,弦BC∥OA,连结AC,则图中阴影部分的面积为( )
A、 B、 C、 D、
6、如图,在△ABC中,∠BAC=300,AC=,BC=,以直线AB为轴旋转一周得到一个几何体,则这个几何体的表面积是( )
A、 B、 C、 D、
二、填空题:
1、扇形的圆心角为1500,扇形的面积为cm2,则扇形的弧长为 。
2、一个圆锥形零件底面圆半径为4 cm,母线长为12 cm,则这个零件的展开图的圆心角的度数是 。
3、如图,正△ABC的中心O恰好为扇形ODE的圆心,要使扇形ODE绕O无论怎样旋转,△ABC与扇形重叠部分的面积总等于△ABC的面积的,则扇形的圆心角应为 。
4、如图,A、B、C、D是圆周上的四个点,,且弦AB=8,CD=4,则图中两个弓形(阴影)面积的和是 (结果保留三个有效数字)。
5、目前,全国人民都在积极支持北京的申奥活动,你们知道吗?国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,每个圆环的内、外圆直径分别为8和10,图中两两相交成的小曲边四边形(阴影部分)的面积相等,已知五个圆环覆盖的面积是122.5平方单位,请你计算出每个小曲边四边形的面积为 平方单位(取3.14)
三、计算或证明题:
1、如图,⊙O内切于△ABC,切点分别为D、E、F,若∠C=900,AD=4,BD=6,求图中阴影部分的面积。
如图,在Rt△ABC中,∠C=900,O点在AB上,半圆O切AC于D,切BC于E,AO=15cm,BO=20cm,求的长。
3、如图,有一个直径是1米圆形铁皮,要从中剪出一个最大的圆心角为900的扇形ABC,求:
(1)被剪掉(阴影)部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?
教师
班级
学生
日期:
上课时间:
主课题:正多边形和圆、弧长公式及有关计算
教学目标:
1. 正多边形的有关概念;正多边形、正多边形的中心、半径、边心距、中心角。正n边形的半径,边心距把正n边形分成2n个全等的直角三角形。
2. 正多边形和圆的关系定理
教学重难点:
1、正多边形和圆关系,弧长公式及应用。
2、正多边形的计算可转化为解直角三角形的问题。
3、解决有关正多边形和圆的计算,应用弧长公式。
教学内容
【同步检测】
1、 正六边形两条对边之间的距离是2,则它的边长是( )
A. B. C. D.
2、如图,两相交圆的公共弦AB为,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比。
【知识精讲】
、重点梳理
、经典例题
例1、如图,扇形OAB的圆心角为,分别以OA、OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( ) A.P=Q B.P>Q C.Q>P D.无法确定
变式训练:如图,△ABC中,,,,分别以AC、BC为直径作半圆,则图中阴影的面积为( ) A. B. C. D.
例2、如图,与相切于点,与轴交于,两点,且、是一元二次方程的两个实数根,求的半径及图中阴影部分的面积.
变式训练:如图,的半径为1,正方形ABCD顶点B坐标为(5,0),顶点D在上运动. ①当点D运动到与点A、O在同一条直线上时,试证明直线CD与 相切; ②当直线CD与相切时,求CD所在直线对应的函数关系式; ③设点D的横坐标为,正方形ABCD的面积为S,求S与之间的函数关系式,并求出S的最大值与最小值.
例3、在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,求S3﹣S4的值。
例4、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)△ADF∽△AED;
(2)FG=2;
(3)S△DEF=4.
变式训练:如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°,求证:;
(2)如图②,若,求的值.
例5、如图,已知直角扇形AOB,半径OA=2cm,以OB为直径在扇形内作半圆M,过M引MP∥AO交于P,求与半圆弧及MP围成的阴影部分面积。
连结OP
(三)、当堂检测
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=600,求阴影部分的周长。
【提高训练】
如图,大小两个同心圆的圆心为O,现任作小圆的三条切线分别交于A、B、C点,记△ABC的面积为,以A、B、C为顶点的三个阴影部分的面积分别为、、,试判断是否为定值,若是,求出这个定值;若不是,请说明理由。
2、如图,⊙O与⊙外切于M,AB、CD是它们的外公切线,A、B、C、D为切点,⊥OA于E,且∠AOC=1200。
(1)求证:⊙的周长等于的弧长;
(2)若⊙的半径为1cm,求图中阴影部分的面积。
【课后练习】
一、选择题:
1、正六边形的两条平行边之间的距离为1,则它的边长为( )
A、 B、 C、 D、
2、如图,两同心圆间的圆环的面积为,过小圆上任一点P作大圆的弦AB,则 的值是( )
A、16 B、 C、4 D、
3、如图,AB为半圆O的直径,C为半圆上一点,且为半圆的,设扇形AOC、△COB、弓形BC的面积分别为、、,则下列结论正确的是( )
A、<< B、<<
C、<< D、<<
4、如图,⊙O1和⊙O2外切于P,它们的外公切线与两圆分别相切于点A、B,设⊙O1的半径为,⊙O2的半径为,的长为,的长为,若,则( )
A、 B、 C、 D、
5、如图,A是半径为1的⊙O外一点,OA=2,AB切⊙O于B,弦BC∥OA,连结AC,则图中阴影部分的面积为( )
A、 B、 C、 D、
6、如图,在△ABC中,∠BAC=300,AC=,BC=,以直线AB为轴旋转一周得到一个几何体,则这个几何体的表面积是( )
A、 B、 C、 D、
二、填空题:
1、扇形的圆心角为1500,扇形的面积为cm2,则扇形的弧长为 。
2、一个圆锥形零件底面圆半径为4 cm,母线长为12 cm,则这个零件的展开图的圆心角的度数是 。
3、如图,正△ABC的中心O恰好为扇形ODE的圆心,要使扇形ODE绕O无论怎样旋转,△ABC与扇形重叠部分的面积总等于△ABC的面积的,则扇形的圆心角应为 。
4、如图,A、B、C、D是圆周上的四个点,,且弦AB=8,CD=4,则图中两个弓形(阴影)面积的和是 (结果保留三个有效数字)。
5、目前,全国人民都在积极支持北京的申奥活动,你们知道吗?国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,每个圆环的内、外圆直径分别为8和10,图中两两相交成的小曲边四边形(阴影部分)的面积相等,已知五个圆环覆盖的面积是122.5平方单位,请你计算出每个小曲边四边形的面积为 平方单位(取3.14)
三、计算或证明题:
1、如图,⊙O内切于△ABC,切点分别为D、E、F,若∠C=900,AD=4,BD=6,求图中阴影部分的面积。
如图,在Rt△ABC中,∠C=900,O点在AB上,半圆O切AC于D,切BC于E,AO=15cm,BO=20cm,求的长。
3、如图,有一个直径是1米圆形铁皮,要从中剪出一个最大的圆心角为900的扇形ABC,求:
(1)被剪掉(阴影)部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?
同课章节目录
