浙教新版八下6.3反比例函数的应用 同步练习卷(含答案)
文档属性
| 名称 | 浙教新版八下6.3反比例函数的应用 同步练习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 343.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-14 11:19:36 | ||
图片预览

文档简介
浙教新版八下《6.3 反比例函数的应用》同步练习卷
一.选择题(共10小题)(每小题3分,共30分 )
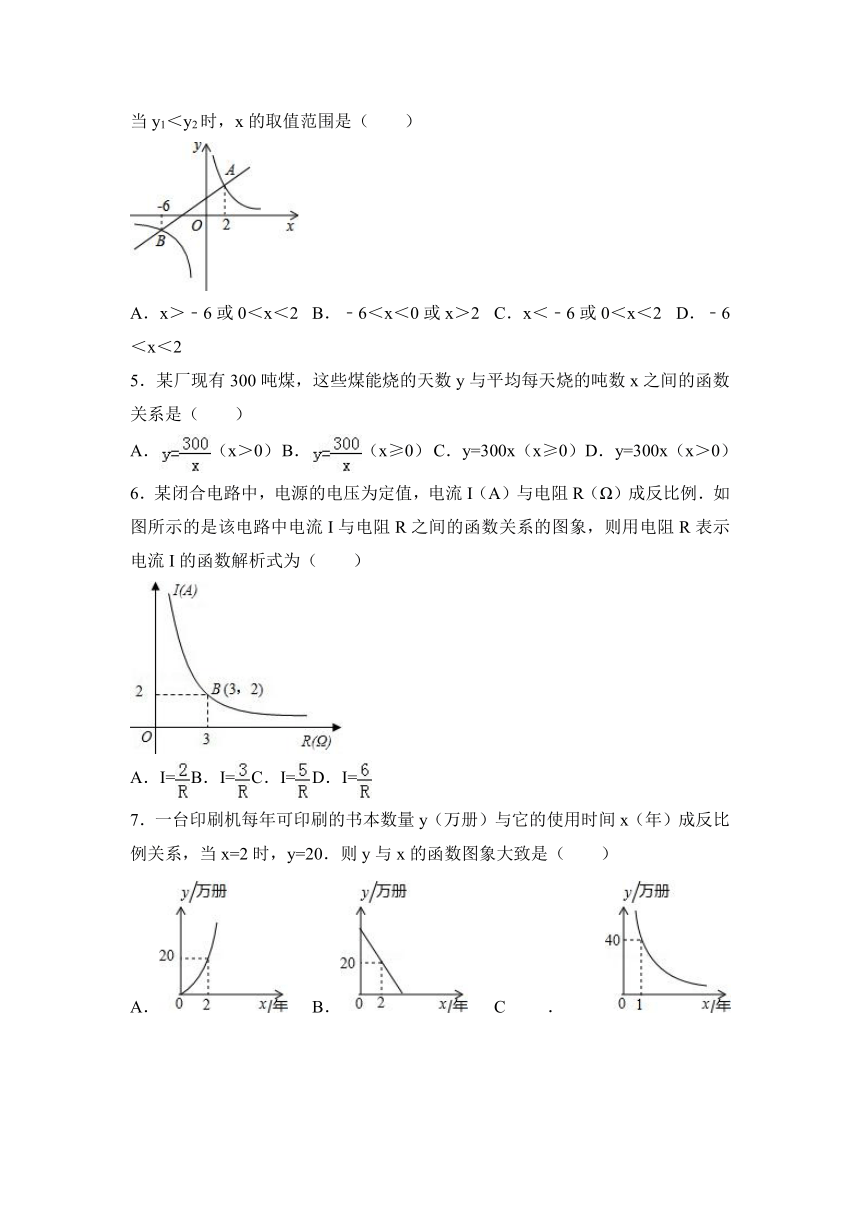
1.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=(k≠0)的图象上,则点E的坐标为( )
A. B.() C.() D.()
2.如图,在反比例函数y=(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
A.4.5 B.4.2 C.4 D.3.8
3.已知点A(﹣2,1),B(1,4),若反比例函数y=与线段AB有公共点时,k的取值范围是( )
A.﹣≤k<0或0<k≤4 B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4 D.﹣2≤k<0或0<k≤4
4.如图,直线y1=x+2与双曲线y2=交于A(2,m)、B(﹣6,n)两点.则当y1<y2时,x的取值范围是( )
A.x>﹣6或0<x<2 B.﹣6<x<0或x>2 C.x<﹣6或0<x<2 D.﹣6<x<2
5.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0) C.y=300x(x≥0) D.y=300x(x>0)
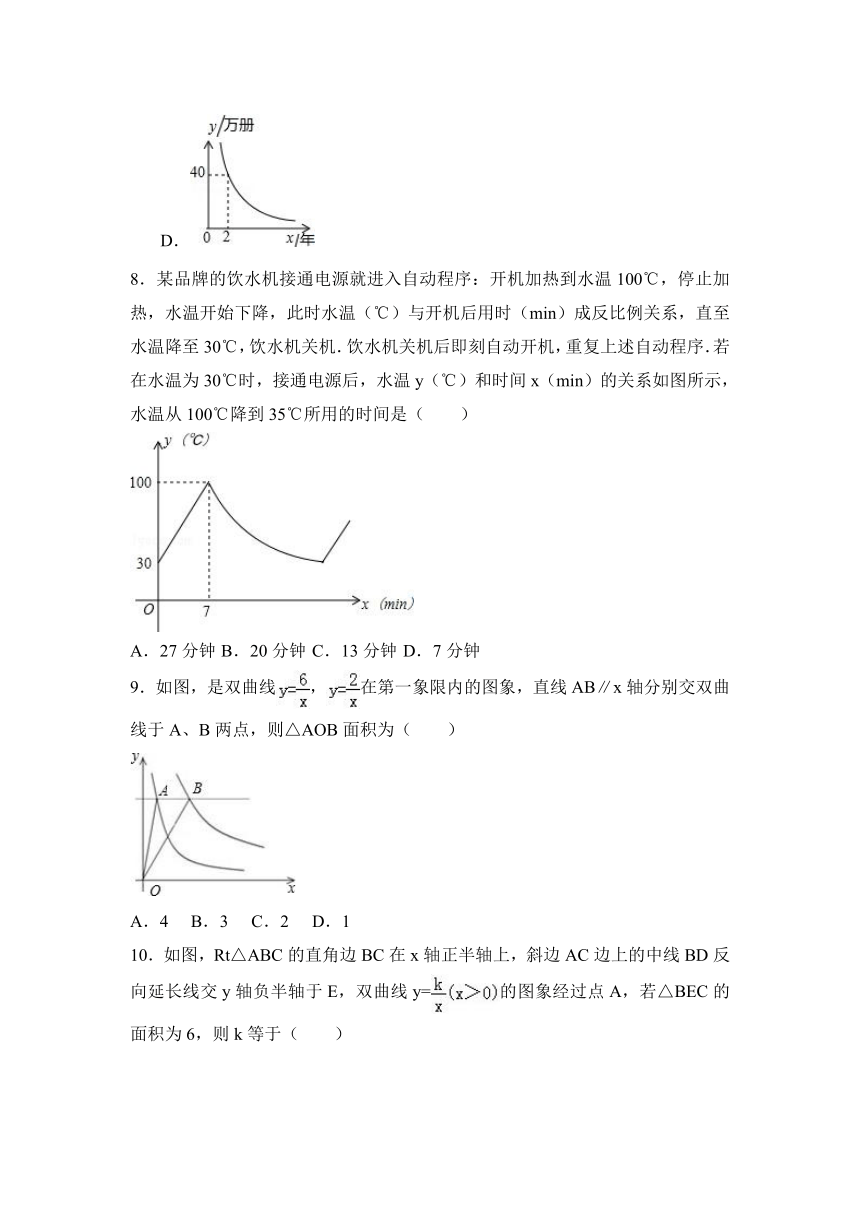
6.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A.I= B.I= C.I= D.I=
7.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B. C. D.
8.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A.27分钟 B.20分钟 C.13分钟 D.7分钟
9.如图,是双曲线,在第一象限内的图象,直线AB∥x轴分别交双曲线于A、B两点,则△AOB面积为( )
A.4 B.3 C.2 D.1
10.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线y=的图象经过点A,若△BEC的面积为6,则k等于( )
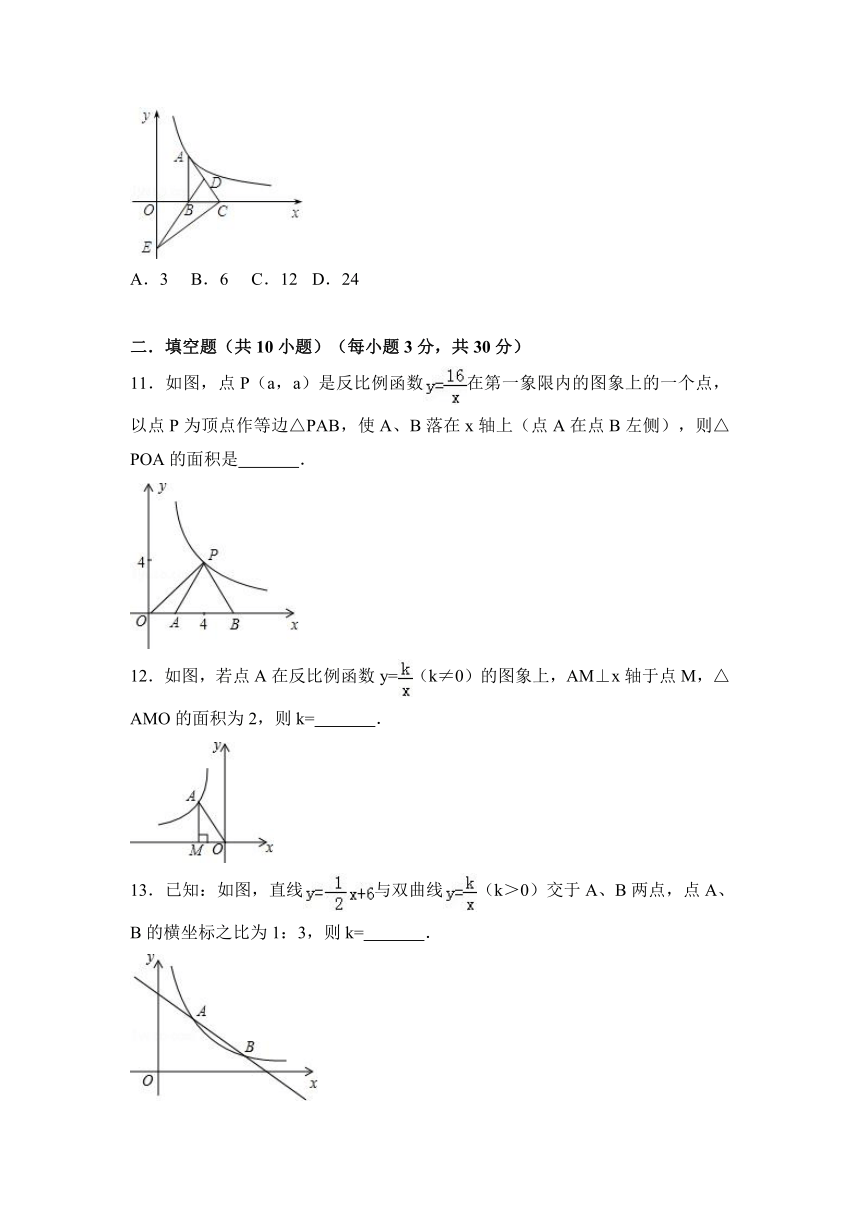
A.3 B.6 C.12 D.24
二.填空题(共10小题)(每小题3分,共30分)
11.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
12.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为2,则k= .
13.已知:如图,直线与双曲线(k>0)交于A、B两点,点A、B的横坐标之比为1:3,则k= .
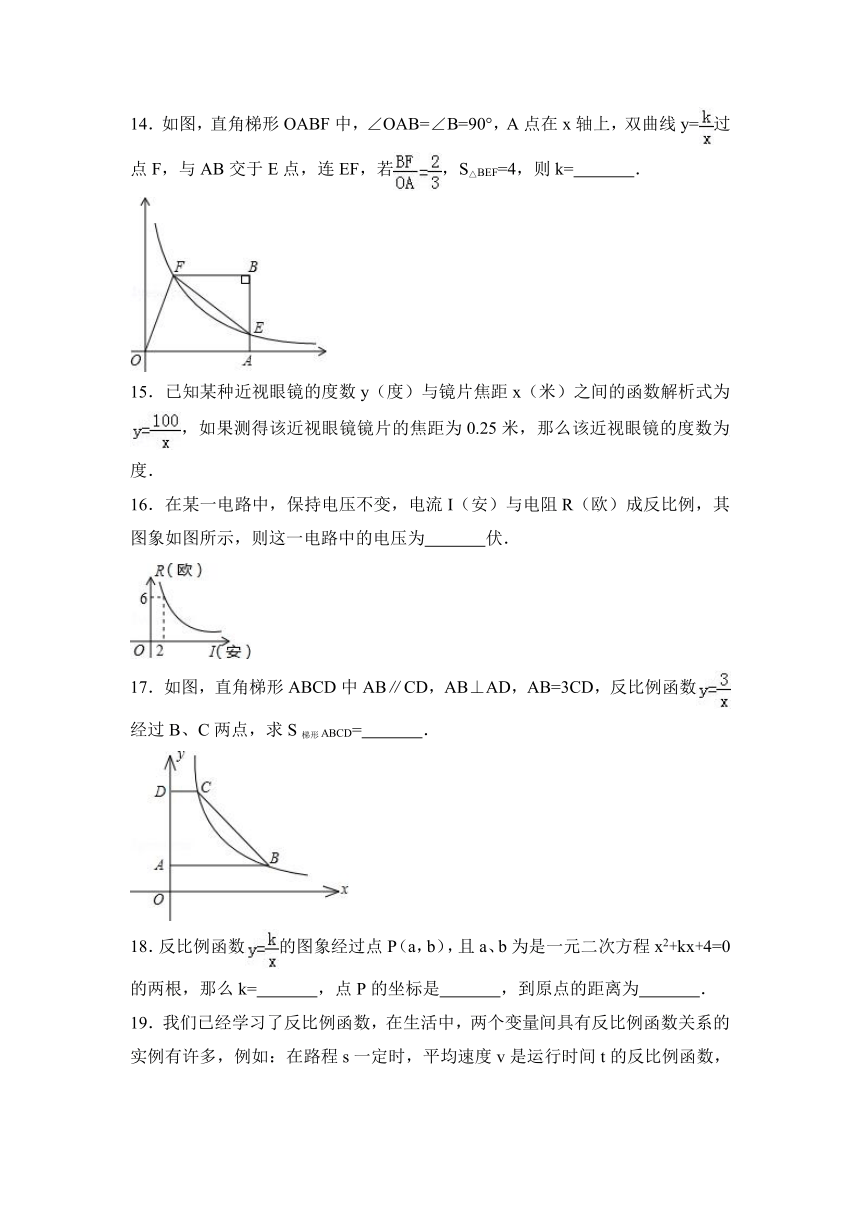
14.如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=过点F,与AB交于E点,连EF,若,S△BEF=4,则k= .
15.已知某种近视眼镜的度数y(度)与镜片焦距x(米)之间的函数解析式为,如果测得该近视眼镜镜片的焦距为0.25米,那么该近视眼镜的度数为 度.
16.在某一电路中,保持电压不变,电流I(安)与电阻R(欧)成反比例,其图象如图所示,则这一电路中的电压为 伏.
17.如图,直角梯形ABCD中AB∥CD,AB⊥AD,AB=3CD,反比例函数经过B、C两点,求S梯形ABCD= .
18.反比例函数的图象经过点P(a,b),且a、b为是一元二次方程x2+kx+4=0的两根,那么k= ,点P的坐标是 ,到原点的距离为 .
19.我们已经学习了反比例函数,在生活中,两个变量间具有反比例函数关系的实例有许多,例如:在路程s一定时,平均速度v是运行时间t的反比例函数,其函数关系式可以写为:v=(s为常数,s≠0).
请你仿照上例,再举一个在日常生活、学习中,两个变量间具有反比例函数关系的实例: ;并写出这两个变量之间的函数解析式: .
20.如图,A、B两点在(x>0)上,如果一个点的横纵坐标均为整数,那么我们称这个点是格点,请写出图中阴影部分(不包括边界)所含格点的个数是 .
三.解答题(共10小题)(每小题4分,共40分)
21.如图,P是反比例函数(k>0)在第一象限图象上的一点,点A的坐标为(2,0).
(1)当点P的横坐标逐渐增大时,△POA的面积将如何变化?
(2)若△POA为等边三角形,求此反比例函数的解析式.
22.已知反比例函数y=的图象与一次函数y=k2x+m的图象交于A(a,1)、B(,﹣3)两点,连结AO.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出k2x+m﹣<0的x的取值范围;
(3)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
23.如图,一次函数y1=k1x+b的图象与反比例函数y2=(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)
(1)求一次函数和反比例函数的解析式;
(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.
24.如图,已知A(﹣4,n),B(3,4)是一次函数y1=kx+b的图象与反比例函数的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线和直线y1=kx+b于P、Q两点.
(1)求反比例函数和一次函数的解析式;
(2)当t为何值时,;
(3)以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线(x>0)始终有交点.
25.在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(m/天)的函数关系图象如图所示,是双曲线的一部分.
(1)请根据题意,求y与x之间的函数表达式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠15米,问该工程队需用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在一个月内(按30天计算)完成任务,那么每天至少要完成多少米?
26.如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=(x>0)图象上,△BOC的面积为8.
(1)求反比例函数y=的关系式;
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式;
(3)当运动时间为秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
27.如图,已知点A(﹣8,n),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数y=图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积,
(3)求方程kx+b﹣=0的解(请直接写出答察);
(4)求不等式kx+b﹣>0的解集(请直接写出答案).
28.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
29.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)求k的值;
(2)现在栽培一种在自然光照且温度为16℃到18℃的条件下生长最快的新品种,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内生长最快的时间是多少小时?
30.如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=的图象经过点B;反比例函数y2=的图象经过点C(,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
浙教新版八下《6.3 反比例函数的应用》同步练习卷答案
一.选择题(共10小题)
1.A.2.C.3.A.4.C.5.A.6.D.7.C.8.C.9.C.10.C.
二.填空题(共10小题)
11.. 12.﹣4. 13.. 14.6. 15.400.
16.12. 17.4. 18.4、(﹣2,﹣2)、2.
19.矩形的面积S一定时,矩形的长a是矩形的宽b的反比例函数;a=(S为常数,且S≠0).
20.3.
三.解答题(共10小题)
21.解:(1)设P(x,y),则△POA的面积=×OA×y=y.
又∵当k>0时,在每一个象限内,y随x的增大而减小.
故当点P的横坐标逐渐增大时,△POA的面积将逐渐减小;
(2)过点P作PC⊥OA,垂足为C,
∵△POA为等边三角形,OA=2,
∴OC=1,,
∴,
代入,得,
所以反比例函数的解析式为.
22.解:(1)∵反比例函数y=的图象经过B(,﹣3),
∴k1=3××(﹣3)=﹣3,
∵反比例函数y=的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得:,
解得.
∴反比例函数关系式为y=﹣,一次函数关系式为y=﹣3x﹣2;
(2)k2x+m﹣<0的x的取值范围为﹣1<x<0或x>;
(3)OA==,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,﹣)或(0,).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣)或(0,)或(0,2)或(0,1).
23.解:(1)∵反比例函数y2=(x>0)的图象经过(2,1),
∴k2=2,
∴反比例函数的解析式为:y2=,
∵一次函数y1=k1x+b的图象经过(2,1)和(0,3),
∴,
解得,,
∴一次函数的解析式为:y1=﹣x+3;
(2)作点B关于x轴的对称点B′,连接AB′交x轴于P,则点P即为所求,
,
解得,,,
则点B的坐标为(1,2),
则点B关于x轴的对称点B′的坐标为(1,﹣2),
设直线AB′的解析式为y=ax+c,
,
解得,,
则直线AB′的解析式为y=3x﹣5,
3x﹣5=0,
解得,x=,
∴点p的坐标为(,0).
24.解:(1)将B(3,4)代入,得m=3×4=12,
∴反比例函数解析式为,
将A(﹣4,n)代入反比例函数,得n=﹣3,
∴A(﹣4,﹣3)
∵直线y1=kx+b过点A和点B,
∴,解得,
∴一次函数的解析式为y=x+1;
(2)如图1,∵PQ⊥x轴,
∴以PQ为底边时,△APQ与△BPQ的面积之比等于PQ边上的高之比,
又∵,
∴,
∵点D(t,0),A(﹣4,﹣3),B(3,4),
∴,即,
解得;
(3)如图2,设直线QM与双曲线交于C点.
依题意可知:P(t,),Q(t,t+1),C(,t+1),
∴QM=PQ=,QC=,
∴QM﹣QC==,
∵0<t<3,
∴0<t(t+1)<12,
∴>1,
即QM﹣QC>0,
∴QM>QC,
即边QM与双曲线始终有交点.
25.解:(1)设y=.
∵点(24,50)在其图象上,
∴所求函数表达式为y=;
(2)由图象,知共需开挖水渠24×50=1200(m);
2台挖掘机需要1200÷(2×15)=40天;
(3)1200÷30=40(m).
故每天至少要完成40m.
26.解:(1)∵四边形AOCB为正方形,
∴AB=BC=OC=OA,
设点B坐标为(a,a),
∵S△BOC=8,
∴a2=8,
∴a=±4
又∵点B在第一象限
点B坐标为(4,4),
将点B(4,4)代入y=得,
k=16,
∴反比例函数解析式为y=;
(2)∵运动时间为t,
∴AE=t,BF=2t,
∵AB=4,∴BE=4﹣t,
∴S△BEF=(4﹣t)?2t
=﹣t2+4t;
(3)存在.
当t=时,点E的坐标为(,4),点F的坐标为(4,),
①作F点关于x轴的对称点F1,得F1(4,﹣),经过点E、F1作直线,
由E(,4),F1(4,﹣)代入y=ax+b得,
,
解得:,
可得直线EF1的解析式是y=﹣2x+;
当y=0时,x=,
∴P点的坐标为(,0)
②作E点关于y轴的对称点E1,得E1(﹣,4),经过点E1、F作直线,
由E1(﹣,4),F(4,)设解析式为:y=kx+c,
代入得:,
解得:,
可得直线E1F的解析式是:y=﹣x+,
当x=0时,y=,
∴P点的坐标为(0,),
∴P点的坐标分别为(,0)或(0,).
27.解:(1)∵B(3,﹣8)在反比例函数y=图象上,
∴﹣8=,m=﹣24,反比例函数的解析式为y=﹣,
把A(﹣8,n)代入y=﹣,n=3,
设一次函数解析式为y=kx+b,
,
解得,,
一次函数解析式为y=﹣x﹣5.
(2)﹣x﹣5=0,x=﹣5,
点C的坐标为(﹣5,0),
△AOB的面积=△AOC的面积+△BOC的面积
=×5×3+×5×8=.
(3)点A(﹣8,3),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数y=图象的两个交点,
方程kx+b﹣=0的解是:x1=﹣8,x2=3,
(4)由图象可知,当x<﹣8或0<x<3时,kx+b>,
∴不等式kx+b﹣>0的解集为:x<﹣8或0<x<3.
28.解:(1)当0≤x≤15时,设y=ax(a≠0);当x≥15时,设y=(k≠0).
将(15,20)代入y=ax,
20=15a,解得:a=,
∴y=x(0≤x≤15).
将(15,20)代入y=,
20=,解得:k=300,
∴y=(x≥15).
(2)当y=x=8时,x=6;
当y==8时,x=37.5.
37.5﹣6=31.5(分钟).
答:有效消毒时间是31.5分钟.
29.解:(1)∵点B(12,18)在双曲线y=上,
∴,
解得:k=216.
(2)线段AD的解析式是y=4x+10,当y=16时,x=1.5
当y=16时,x==13.5
所以时间为13.5﹣1.5=12小时.
30.解:(1)∵CA⊥x轴,∠ACB=90°,
∴CB∥x轴.
∵将C(,m)代入函数y2=得:n==,
∴点C(,).
∴点B的纵坐标为.
∵将y1=代入得:=,解得;x=2,
∴点B的坐标为(2,).
(2)如图所示:连接ME、MD、MF.
∵⊙M与BC,CA,AB分别相切于D,E,F,
∴ME⊥AC,MD⊥BC,MF⊥AB.
∴∠ECD=∠CDM=∠CEM=90°.
∴四边形CDME为矩形.
∵MD=ME,
∴四边形CDME为正方形.
∵在Rt△ACB中,AC=,BC=,
∴AB=2.
∵S△ACB=AC?BC=(AC+BC+AB)?r,
∴⊙M的半径===﹣1.
∴点M的坐标为(2﹣1,1).
一.选择题(共10小题)(每小题3分,共30分 )
1.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=(k≠0)的图象上,则点E的坐标为( )
A. B.() C.() D.()
2.如图,在反比例函数y=(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
A.4.5 B.4.2 C.4 D.3.8
3.已知点A(﹣2,1),B(1,4),若反比例函数y=与线段AB有公共点时,k的取值范围是( )
A.﹣≤k<0或0<k≤4 B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4 D.﹣2≤k<0或0<k≤4
4.如图,直线y1=x+2与双曲线y2=交于A(2,m)、B(﹣6,n)两点.则当y1<y2时,x的取值范围是( )
A.x>﹣6或0<x<2 B.﹣6<x<0或x>2 C.x<﹣6或0<x<2 D.﹣6<x<2
5.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0) C.y=300x(x≥0) D.y=300x(x>0)
6.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A.I= B.I= C.I= D.I=
7.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B. C. D.
8.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A.27分钟 B.20分钟 C.13分钟 D.7分钟
9.如图,是双曲线,在第一象限内的图象,直线AB∥x轴分别交双曲线于A、B两点,则△AOB面积为( )
A.4 B.3 C.2 D.1
10.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线y=的图象经过点A,若△BEC的面积为6,则k等于( )
A.3 B.6 C.12 D.24
二.填空题(共10小题)(每小题3分,共30分)
11.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
12.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为2,则k= .
13.已知:如图,直线与双曲线(k>0)交于A、B两点,点A、B的横坐标之比为1:3,则k= .
14.如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=过点F,与AB交于E点,连EF,若,S△BEF=4,则k= .
15.已知某种近视眼镜的度数y(度)与镜片焦距x(米)之间的函数解析式为,如果测得该近视眼镜镜片的焦距为0.25米,那么该近视眼镜的度数为 度.
16.在某一电路中,保持电压不变,电流I(安)与电阻R(欧)成反比例,其图象如图所示,则这一电路中的电压为 伏.
17.如图,直角梯形ABCD中AB∥CD,AB⊥AD,AB=3CD,反比例函数经过B、C两点,求S梯形ABCD= .
18.反比例函数的图象经过点P(a,b),且a、b为是一元二次方程x2+kx+4=0的两根,那么k= ,点P的坐标是 ,到原点的距离为 .
19.我们已经学习了反比例函数,在生活中,两个变量间具有反比例函数关系的实例有许多,例如:在路程s一定时,平均速度v是运行时间t的反比例函数,其函数关系式可以写为:v=(s为常数,s≠0).
请你仿照上例,再举一个在日常生活、学习中,两个变量间具有反比例函数关系的实例: ;并写出这两个变量之间的函数解析式: .
20.如图,A、B两点在(x>0)上,如果一个点的横纵坐标均为整数,那么我们称这个点是格点,请写出图中阴影部分(不包括边界)所含格点的个数是 .
三.解答题(共10小题)(每小题4分,共40分)
21.如图,P是反比例函数(k>0)在第一象限图象上的一点,点A的坐标为(2,0).
(1)当点P的横坐标逐渐增大时,△POA的面积将如何变化?
(2)若△POA为等边三角形,求此反比例函数的解析式.
22.已知反比例函数y=的图象与一次函数y=k2x+m的图象交于A(a,1)、B(,﹣3)两点,连结AO.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出k2x+m﹣<0的x的取值范围;
(3)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
23.如图,一次函数y1=k1x+b的图象与反比例函数y2=(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)
(1)求一次函数和反比例函数的解析式;
(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.
24.如图,已知A(﹣4,n),B(3,4)是一次函数y1=kx+b的图象与反比例函数的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线和直线y1=kx+b于P、Q两点.
(1)求反比例函数和一次函数的解析式;
(2)当t为何值时,;
(3)以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线(x>0)始终有交点.
25.在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(m/天)的函数关系图象如图所示,是双曲线的一部分.
(1)请根据题意,求y与x之间的函数表达式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠15米,问该工程队需用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在一个月内(按30天计算)完成任务,那么每天至少要完成多少米?
26.如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=(x>0)图象上,△BOC的面积为8.
(1)求反比例函数y=的关系式;
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式;
(3)当运动时间为秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
27.如图,已知点A(﹣8,n),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数y=图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积,
(3)求方程kx+b﹣=0的解(请直接写出答察);
(4)求不等式kx+b﹣>0的解集(请直接写出答案).
28.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
29.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)求k的值;
(2)现在栽培一种在自然光照且温度为16℃到18℃的条件下生长最快的新品种,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内生长最快的时间是多少小时?
30.如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=的图象经过点B;反比例函数y2=的图象经过点C(,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
浙教新版八下《6.3 反比例函数的应用》同步练习卷答案
一.选择题(共10小题)
1.A.2.C.3.A.4.C.5.A.6.D.7.C.8.C.9.C.10.C.
二.填空题(共10小题)
11.. 12.﹣4. 13.. 14.6. 15.400.
16.12. 17.4. 18.4、(﹣2,﹣2)、2.
19.矩形的面积S一定时,矩形的长a是矩形的宽b的反比例函数;a=(S为常数,且S≠0).
20.3.
三.解答题(共10小题)
21.解:(1)设P(x,y),则△POA的面积=×OA×y=y.
又∵当k>0时,在每一个象限内,y随x的增大而减小.
故当点P的横坐标逐渐增大时,△POA的面积将逐渐减小;
(2)过点P作PC⊥OA,垂足为C,
∵△POA为等边三角形,OA=2,
∴OC=1,,
∴,
代入,得,
所以反比例函数的解析式为.
22.解:(1)∵反比例函数y=的图象经过B(,﹣3),
∴k1=3××(﹣3)=﹣3,
∵反比例函数y=的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得:,
解得.
∴反比例函数关系式为y=﹣,一次函数关系式为y=﹣3x﹣2;
(2)k2x+m﹣<0的x的取值范围为﹣1<x<0或x>;
(3)OA==,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,﹣)或(0,).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣)或(0,)或(0,2)或(0,1).
23.解:(1)∵反比例函数y2=(x>0)的图象经过(2,1),
∴k2=2,
∴反比例函数的解析式为:y2=,
∵一次函数y1=k1x+b的图象经过(2,1)和(0,3),
∴,
解得,,
∴一次函数的解析式为:y1=﹣x+3;
(2)作点B关于x轴的对称点B′,连接AB′交x轴于P,则点P即为所求,
,
解得,,,
则点B的坐标为(1,2),
则点B关于x轴的对称点B′的坐标为(1,﹣2),
设直线AB′的解析式为y=ax+c,
,
解得,,
则直线AB′的解析式为y=3x﹣5,
3x﹣5=0,
解得,x=,
∴点p的坐标为(,0).
24.解:(1)将B(3,4)代入,得m=3×4=12,
∴反比例函数解析式为,
将A(﹣4,n)代入反比例函数,得n=﹣3,
∴A(﹣4,﹣3)
∵直线y1=kx+b过点A和点B,
∴,解得,
∴一次函数的解析式为y=x+1;
(2)如图1,∵PQ⊥x轴,
∴以PQ为底边时,△APQ与△BPQ的面积之比等于PQ边上的高之比,
又∵,
∴,
∵点D(t,0),A(﹣4,﹣3),B(3,4),
∴,即,
解得;
(3)如图2,设直线QM与双曲线交于C点.
依题意可知:P(t,),Q(t,t+1),C(,t+1),
∴QM=PQ=,QC=,
∴QM﹣QC==,
∵0<t<3,
∴0<t(t+1)<12,
∴>1,
即QM﹣QC>0,
∴QM>QC,
即边QM与双曲线始终有交点.
25.解:(1)设y=.
∵点(24,50)在其图象上,
∴所求函数表达式为y=;
(2)由图象,知共需开挖水渠24×50=1200(m);
2台挖掘机需要1200÷(2×15)=40天;
(3)1200÷30=40(m).
故每天至少要完成40m.
26.解:(1)∵四边形AOCB为正方形,
∴AB=BC=OC=OA,
设点B坐标为(a,a),
∵S△BOC=8,
∴a2=8,
∴a=±4
又∵点B在第一象限
点B坐标为(4,4),
将点B(4,4)代入y=得,
k=16,
∴反比例函数解析式为y=;
(2)∵运动时间为t,
∴AE=t,BF=2t,
∵AB=4,∴BE=4﹣t,
∴S△BEF=(4﹣t)?2t
=﹣t2+4t;
(3)存在.
当t=时,点E的坐标为(,4),点F的坐标为(4,),
①作F点关于x轴的对称点F1,得F1(4,﹣),经过点E、F1作直线,
由E(,4),F1(4,﹣)代入y=ax+b得,
,
解得:,
可得直线EF1的解析式是y=﹣2x+;
当y=0时,x=,
∴P点的坐标为(,0)
②作E点关于y轴的对称点E1,得E1(﹣,4),经过点E1、F作直线,
由E1(﹣,4),F(4,)设解析式为:y=kx+c,
代入得:,
解得:,
可得直线E1F的解析式是:y=﹣x+,
当x=0时,y=,
∴P点的坐标为(0,),
∴P点的坐标分别为(,0)或(0,).
27.解:(1)∵B(3,﹣8)在反比例函数y=图象上,
∴﹣8=,m=﹣24,反比例函数的解析式为y=﹣,
把A(﹣8,n)代入y=﹣,n=3,
设一次函数解析式为y=kx+b,
,
解得,,
一次函数解析式为y=﹣x﹣5.
(2)﹣x﹣5=0,x=﹣5,
点C的坐标为(﹣5,0),
△AOB的面积=△AOC的面积+△BOC的面积
=×5×3+×5×8=.
(3)点A(﹣8,3),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数y=图象的两个交点,
方程kx+b﹣=0的解是:x1=﹣8,x2=3,
(4)由图象可知,当x<﹣8或0<x<3时,kx+b>,
∴不等式kx+b﹣>0的解集为:x<﹣8或0<x<3.
28.解:(1)当0≤x≤15时,设y=ax(a≠0);当x≥15时,设y=(k≠0).
将(15,20)代入y=ax,
20=15a,解得:a=,
∴y=x(0≤x≤15).
将(15,20)代入y=,
20=,解得:k=300,
∴y=(x≥15).
(2)当y=x=8时,x=6;
当y==8时,x=37.5.
37.5﹣6=31.5(分钟).
答:有效消毒时间是31.5分钟.
29.解:(1)∵点B(12,18)在双曲线y=上,
∴,
解得:k=216.
(2)线段AD的解析式是y=4x+10,当y=16时,x=1.5
当y=16时,x==13.5
所以时间为13.5﹣1.5=12小时.
30.解:(1)∵CA⊥x轴,∠ACB=90°,
∴CB∥x轴.
∵将C(,m)代入函数y2=得:n==,
∴点C(,).
∴点B的纵坐标为.
∵将y1=代入得:=,解得;x=2,
∴点B的坐标为(2,).
(2)如图所示:连接ME、MD、MF.
∵⊙M与BC,CA,AB分别相切于D,E,F,
∴ME⊥AC,MD⊥BC,MF⊥AB.
∴∠ECD=∠CDM=∠CEM=90°.
∴四边形CDME为矩形.
∵MD=ME,
∴四边形CDME为正方形.
∵在Rt△ACB中,AC=,BC=,
∴AB=2.
∵S△ACB=AC?BC=(AC+BC+AB)?r,
∴⊙M的半径===﹣1.
∴点M的坐标为(2﹣1,1).
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
