浙教新版八年级下学期6.2反比例函数的图象和性质 同步练习卷(含答案)
文档属性
| 名称 | 浙教新版八年级下学期6.2反比例函数的图象和性质 同步练习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-14 11:25:35 | ||
图片预览




文档简介
浙教新版八下《6.2 反比例函数的图象和性质》同步练习卷
一.选择题(共15小题)(每小题2分,共30分)
1.若,,则x的取值范围( )
A. B.或
C.或 D.以上答案都不对
2.已知点A(x1,y1),(x2,y2)是反比例函数y=图象上的点,若x1>0>x2,则一定成立的是( )
A.y1>y2>0 B.y1>0>y2 C.0>y1>y2 D.y2>0>y1
3.如果点A(x1,y1)和点B(x2,y2)是直线y=kx﹣b上的两点,且当x1<x2时,y1<y2,那么函数y=的图象位于( )象限.
A.一、四 B.二、四 C.三、四 D.一、三
4.若双曲线位于第二、四象限,则k的取值范围是( )
A.k<1 B.k≥1 C.k>1 D.k≠1
5.如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
6.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=(k≠0)的图象上,则点E的坐标为( )
A. B.() C.() D.()
7.若M(,y1)、N(,y2)、P(,y3)三点都在函数(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y2>y3>y1 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
8.点(x1,y1)、(x2,y2)、(x3,y3)在反比例函数的图象上,且x1<0<x2<x3,则有( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1
9.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2 B.k<﹣2 C.k>2 D.k<2
10.如图,A,B,C为反比例函数图象上的三个点,分别从A,B,C向xy轴作垂线,构成三个矩形,它们的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是( )
A.S1=S2>S3 B.S1<S2<S3 C.S1>S2>S3 D.S1=S2=S3
11.在反比例函数y=的图象的每一个象限内,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k≥3 D.k<3
12.已知函数图象如图,以下结论,其中正确有( )个:
①m<0;
②在每个分支上y随x的增大而增大;
③若A(﹣1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
A.4个 B.3个 C.2个 D.1个
13.如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )
A.S1>S2>S3 B.S3>S2>S1 C.S1=S2=S3 D.S2>S3>S1
14.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A,B两点,若S△AOB=2,则k2﹣k1的值是( )
A.1 B.2 C.4 D.8
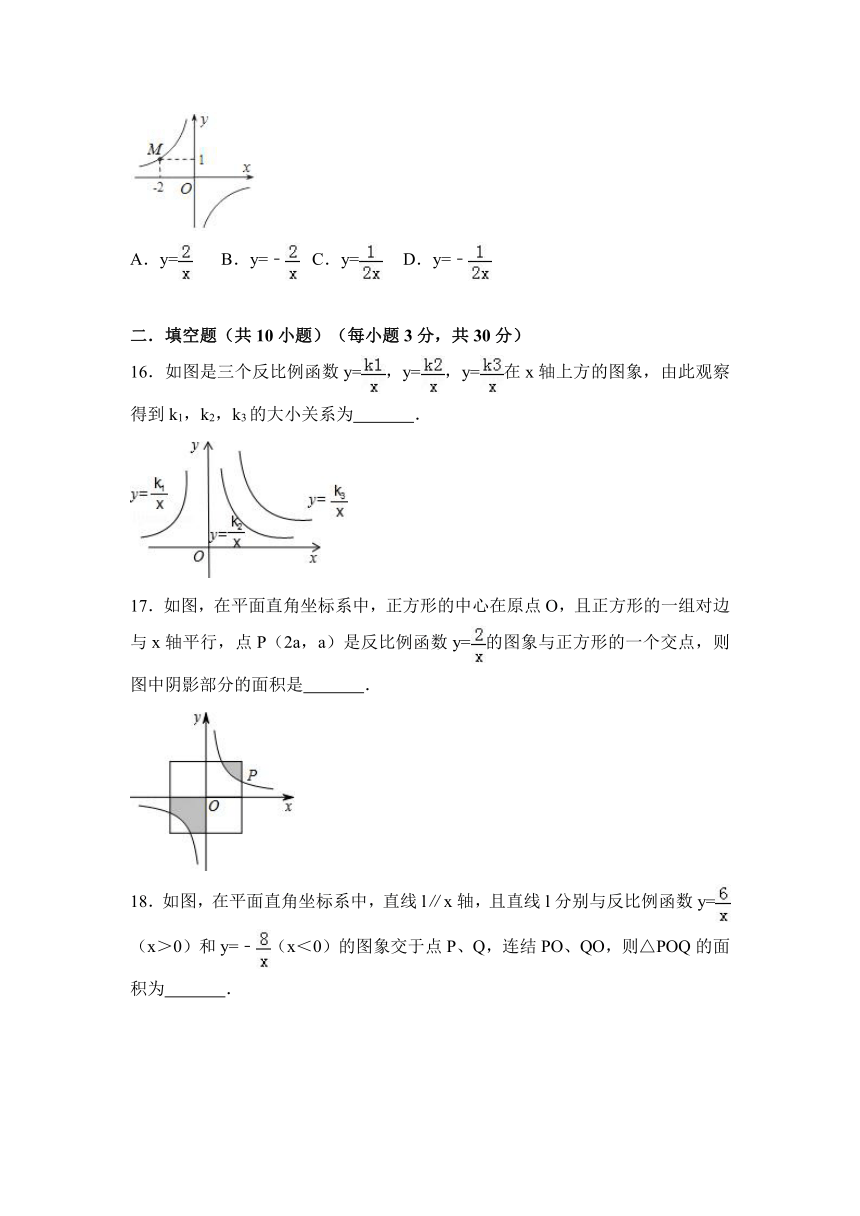
15.如图,某反比例函数的图象过点M(﹣2,1),则此反比例函数表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
二.填空题(共10小题)(每小题3分,共30分)
16.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
17.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=的图象与正方形的一个交点,则图中阴影部分的面积是 .
18.如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=(x>0)和y=﹣(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
19.已知点A(2,y1),B(1,y2)在反比例函数y=(k<0)的图象上,则y1 y2.(选填“>”、“=”、“<”)
20.如图所示是三个反比例函数y=,y=,y=的图象,由此观察k1、k2、k3的大小关系是 .(用“<”连接)
21.有一个函数具备以下两个特点:(1)与直线y=﹣x有两个交点;(2)图象上任意一点到两坐标轴的距离的积都为5,请写出这个函数解析式 .
22.如图,在平面直角坐标系中,点P(3a,a)是反比例函y=与⊙O的一个交点,则图中阴影部分的面积为 .
23.点A(2,1)在反比例函数y=的图象上,当y<2时,x的取值范围是 .
24.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于点A,B,若点A的坐标为(﹣2,3),则点B的坐标为 .
25.如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为 .
三.解答题(共8小题)(每小题5分,共40分)
26.(1)画出函数y=﹣(x<0)的图象:
列表:
x
…
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
…
描点并连线.
(2)从图象可以看出,曲线从左向右 ,当x由小变大时,y=﹣(x<0)随之 .
27.已知函数y=(m﹣2)x是反比例函数.
(1)求m的值;
(2)画出函数的图象.
28.如图,双曲线y=(k>0,x>0)的图象上有两点P1(x1,y1)和P2(x2,y2),且x1<x2,分别过P1和P2向x轴作垂线,垂足为B、D.过P1和P2向y轴作垂线,垂足为A、C.
(1)若记四边形AP1BO和四边形CP2DO的面积分别为S1和S2,周长为C1和C2,试比较S1和S2,C1和C2的大小;
(2)若P是双曲线y=(k>0,x>0)的图象上一点,分别过P向x轴、y轴垂线,垂足为M、N.试问当P点落在何处时,四边形PMON的周长最小?
29.已知y=﹣图象上一点到y轴的距离是,求这点的坐标.
30.如果函数y=kx|k|﹣3的图象是双曲线,且在第二、四象限内,求k的值.
31.如图,点P(4,1)在双曲线y=(x>0)上.
(1)则k的值为 ;
(2)若正方形ABCD的顶点B,C在双曲线y=(x>0)上,顶点A,D分别在x轴和y轴的正半轴上,求点C的坐标.
32.如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.
(1)若AD=1,求点F的坐标.
(2)若反比例函数y=的图象经过点E,G两点,求k值.
33.如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴和y轴上,且OA=4,反比例函数y=(x>0)的图象交AB于点D,交BC于点E.
(1)求点D的坐标;
(2)证明:OE=OD.
浙教新版八下《6.2 反比例函数的图象和性质》同步练习卷答案
一.选择题(共15小题)
1.C.2.B.3.D.4.A.5.D.6.A.7.C.8.B.
9.B.10.D.11.D.12.B.13.C.14.C.15.B.
二.填空题(共10小题)
16.k1<k2<k3. 17.4. 18.7. 19.y1>y2. 20.k1<k3<k2.
21.y=﹣. 22.10π. 23.x>1或x<0. 24.(2,﹣3). 25.y=.
三.解答题(共8小题)
26.解:(1)列表:
x
…
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
1
2
3
6
…
函数图象如图;
;
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=﹣(x<0)随之变大.
故答案为:依次升高,变大.
27.解:(1)∵函数y=(m﹣2)x是反比例函数,
∴,
∴m=﹣2;
(2)当m=﹣2时反比例函数的解析式为y=﹣,
图象为:
28.解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;
当y1﹣y2=x2﹣x1,即AC=BD时,C1=C2;
当y1﹣y2<x2﹣x1,即AC<BD时,C1<C2;
当y1﹣y2>x2﹣x1,即AC>BD时,C1>C2.
(2)设P(x,y),即(x,),
四边形PMON的周长=2(x+y)=2(x+),
因为面积相等的四边形中正方形的周长最小,
所以x=,即x2=k,
解得x=,
故P点坐标为(,).
29.解:∵y=﹣图象上一点到y轴的距离是,
∴这个点的横坐标为或﹣,
当x=时,y=﹣=﹣=﹣,此时这个点的坐标为(,﹣);
当x=﹣时,y=﹣==,此时这个点的坐标为(,).
30.解:∵该函数的图象是双曲线且在第二、四象限
∴,
解得,
∴k=﹣2.
31.解:(1)点P(4,1)在双曲线y=上,
将x=4,y=1代入解析式可得:
k=4;
故答案为:4;
(2)过点B作BE⊥OA于点E,过点C作CF⊥OD于点F,
∵四边形ABCD是正方形,
∴AB=AD=DC,∠CDA=90°,
∴∠FDC+∠ODA=90°,
∵∠CFD=∠DOA=90°,
∴∠FCD+∠FDC=90°,
∴∠FDC=∠OAD,
在△CFD和△AOD中,
,
∴△CFD≌△AOD(AAS),
同理可得:△DOA≌△AEB≌△CFD,
∴CF=OD=AE=b,DF=OA=BE=a,
设A(a,0),D(0,b),
则B(a+b,a),C(b,a+b),
可得:b(a+b)=4,a(a+b)=4,
解得:a=b=.
所以点C的坐标为:(,2).
32.解:(1)过F作FN⊥x轴,交CB的延长线于点M,
∵∠FBM+∠MBD=90°∠MBD+∠ABD=90°,
∴∠FBM=∠ABD,
∵四边形OABC是正方形,
∴BF=BD,
在△ABD和△BMF中,,
∴ABD≌△BMF,
∴BM=AB=2,FM=AD=1,
∴F(4,3);
(2)过E作EH⊥x轴,交x轴于点H,
∵∠FBM+∠MBD=90°,∠MBD+∠ABD=90°,
∴∠FBM=∠ABD,
∵四边形BDEF为正方形,
∴BF=BD,
在△ABD和△BMF中,
,
∴△ABD≌△BMF(AAS),
设AD=FM=a,则有F(4,2+a),C(0,2),
由三角形中位线可得G为CF的中点,
∴G(2,2+a),
同理得到△DHE≌△BAD,
∴EH=AD=a,OH=OA+AD+DH=4+a,
∴E(4+a,a),
∴2(2+a)=a(4+a),即a2+3a﹣4=0,
解得:a=1或a=﹣4(舍去),
∴E(5,1),
把F代入反比例解析式得:k=5.
33.(1)解:∵OA=4,
∴A(4,0),
∴当x=4时,y===1,
∴D(4,1);
(2)证明:∵OC=OA=4,
∴E(4,1),
∴CE=AD=1,
在△OCE和△OAD中,
∵,
∴△OCE≌△OAD(SAS),
∴OE=OD
一.选择题(共15小题)(每小题2分,共30分)
1.若,,则x的取值范围( )
A. B.或
C.或 D.以上答案都不对
2.已知点A(x1,y1),(x2,y2)是反比例函数y=图象上的点,若x1>0>x2,则一定成立的是( )
A.y1>y2>0 B.y1>0>y2 C.0>y1>y2 D.y2>0>y1
3.如果点A(x1,y1)和点B(x2,y2)是直线y=kx﹣b上的两点,且当x1<x2时,y1<y2,那么函数y=的图象位于( )象限.
A.一、四 B.二、四 C.三、四 D.一、三
4.若双曲线位于第二、四象限,则k的取值范围是( )
A.k<1 B.k≥1 C.k>1 D.k≠1
5.如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
6.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=(k≠0)的图象上,则点E的坐标为( )
A. B.() C.() D.()
7.若M(,y1)、N(,y2)、P(,y3)三点都在函数(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y2>y3>y1 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
8.点(x1,y1)、(x2,y2)、(x3,y3)在反比例函数的图象上,且x1<0<x2<x3,则有( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1
9.若反比例函数y=,当x<0时,y随x的增大而增大,则k的取值范围是( )
A.k>﹣2 B.k<﹣2 C.k>2 D.k<2
10.如图,A,B,C为反比例函数图象上的三个点,分别从A,B,C向xy轴作垂线,构成三个矩形,它们的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是( )
A.S1=S2>S3 B.S1<S2<S3 C.S1>S2>S3 D.S1=S2=S3
11.在反比例函数y=的图象的每一个象限内,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k≥3 D.k<3
12.已知函数图象如图,以下结论,其中正确有( )个:
①m<0;
②在每个分支上y随x的增大而增大;
③若A(﹣1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
A.4个 B.3个 C.2个 D.1个
13.如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )
A.S1>S2>S3 B.S3>S2>S1 C.S1=S2=S3 D.S2>S3>S1
14.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A,B两点,若S△AOB=2,则k2﹣k1的值是( )
A.1 B.2 C.4 D.8
15.如图,某反比例函数的图象过点M(﹣2,1),则此反比例函数表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
二.填空题(共10小题)(每小题3分,共30分)
16.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
17.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=的图象与正方形的一个交点,则图中阴影部分的面积是 .
18.如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=(x>0)和y=﹣(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
19.已知点A(2,y1),B(1,y2)在反比例函数y=(k<0)的图象上,则y1 y2.(选填“>”、“=”、“<”)
20.如图所示是三个反比例函数y=,y=,y=的图象,由此观察k1、k2、k3的大小关系是 .(用“<”连接)
21.有一个函数具备以下两个特点:(1)与直线y=﹣x有两个交点;(2)图象上任意一点到两坐标轴的距离的积都为5,请写出这个函数解析式 .
22.如图,在平面直角坐标系中,点P(3a,a)是反比例函y=与⊙O的一个交点,则图中阴影部分的面积为 .
23.点A(2,1)在反比例函数y=的图象上,当y<2时,x的取值范围是 .
24.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于点A,B,若点A的坐标为(﹣2,3),则点B的坐标为 .
25.如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为 .
三.解答题(共8小题)(每小题5分,共40分)
26.(1)画出函数y=﹣(x<0)的图象:
列表:
x
…
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
…
描点并连线.
(2)从图象可以看出,曲线从左向右 ,当x由小变大时,y=﹣(x<0)随之 .
27.已知函数y=(m﹣2)x是反比例函数.
(1)求m的值;
(2)画出函数的图象.
28.如图,双曲线y=(k>0,x>0)的图象上有两点P1(x1,y1)和P2(x2,y2),且x1<x2,分别过P1和P2向x轴作垂线,垂足为B、D.过P1和P2向y轴作垂线,垂足为A、C.
(1)若记四边形AP1BO和四边形CP2DO的面积分别为S1和S2,周长为C1和C2,试比较S1和S2,C1和C2的大小;
(2)若P是双曲线y=(k>0,x>0)的图象上一点,分别过P向x轴、y轴垂线,垂足为M、N.试问当P点落在何处时,四边形PMON的周长最小?
29.已知y=﹣图象上一点到y轴的距离是,求这点的坐标.
30.如果函数y=kx|k|﹣3的图象是双曲线,且在第二、四象限内,求k的值.
31.如图,点P(4,1)在双曲线y=(x>0)上.
(1)则k的值为 ;
(2)若正方形ABCD的顶点B,C在双曲线y=(x>0)上,顶点A,D分别在x轴和y轴的正半轴上,求点C的坐标.
32.如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.
(1)若AD=1,求点F的坐标.
(2)若反比例函数y=的图象经过点E,G两点,求k值.
33.如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴和y轴上,且OA=4,反比例函数y=(x>0)的图象交AB于点D,交BC于点E.
(1)求点D的坐标;
(2)证明:OE=OD.
浙教新版八下《6.2 反比例函数的图象和性质》同步练习卷答案
一.选择题(共15小题)
1.C.2.B.3.D.4.A.5.D.6.A.7.C.8.B.
9.B.10.D.11.D.12.B.13.C.14.C.15.B.
二.填空题(共10小题)
16.k1<k2<k3. 17.4. 18.7. 19.y1>y2. 20.k1<k3<k2.
21.y=﹣. 22.10π. 23.x>1或x<0. 24.(2,﹣3). 25.y=.
三.解答题(共8小题)
26.解:(1)列表:
x
…
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
1
2
3
6
…
函数图象如图;
;
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=﹣(x<0)随之变大.
故答案为:依次升高,变大.
27.解:(1)∵函数y=(m﹣2)x是反比例函数,
∴,
∴m=﹣2;
(2)当m=﹣2时反比例函数的解析式为y=﹣,
图象为:
28.解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;
当y1﹣y2=x2﹣x1,即AC=BD时,C1=C2;
当y1﹣y2<x2﹣x1,即AC<BD时,C1<C2;
当y1﹣y2>x2﹣x1,即AC>BD时,C1>C2.
(2)设P(x,y),即(x,),
四边形PMON的周长=2(x+y)=2(x+),
因为面积相等的四边形中正方形的周长最小,
所以x=,即x2=k,
解得x=,
故P点坐标为(,).
29.解:∵y=﹣图象上一点到y轴的距离是,
∴这个点的横坐标为或﹣,
当x=时,y=﹣=﹣=﹣,此时这个点的坐标为(,﹣);
当x=﹣时,y=﹣==,此时这个点的坐标为(,).
30.解:∵该函数的图象是双曲线且在第二、四象限
∴,
解得,
∴k=﹣2.
31.解:(1)点P(4,1)在双曲线y=上,
将x=4,y=1代入解析式可得:
k=4;
故答案为:4;
(2)过点B作BE⊥OA于点E,过点C作CF⊥OD于点F,
∵四边形ABCD是正方形,
∴AB=AD=DC,∠CDA=90°,
∴∠FDC+∠ODA=90°,
∵∠CFD=∠DOA=90°,
∴∠FCD+∠FDC=90°,
∴∠FDC=∠OAD,
在△CFD和△AOD中,
,
∴△CFD≌△AOD(AAS),
同理可得:△DOA≌△AEB≌△CFD,
∴CF=OD=AE=b,DF=OA=BE=a,
设A(a,0),D(0,b),
则B(a+b,a),C(b,a+b),
可得:b(a+b)=4,a(a+b)=4,
解得:a=b=.
所以点C的坐标为:(,2).
32.解:(1)过F作FN⊥x轴,交CB的延长线于点M,
∵∠FBM+∠MBD=90°∠MBD+∠ABD=90°,
∴∠FBM=∠ABD,
∵四边形OABC是正方形,
∴BF=BD,
在△ABD和△BMF中,,
∴ABD≌△BMF,
∴BM=AB=2,FM=AD=1,
∴F(4,3);
(2)过E作EH⊥x轴,交x轴于点H,
∵∠FBM+∠MBD=90°,∠MBD+∠ABD=90°,
∴∠FBM=∠ABD,
∵四边形BDEF为正方形,
∴BF=BD,
在△ABD和△BMF中,
,
∴△ABD≌△BMF(AAS),
设AD=FM=a,则有F(4,2+a),C(0,2),
由三角形中位线可得G为CF的中点,
∴G(2,2+a),
同理得到△DHE≌△BAD,
∴EH=AD=a,OH=OA+AD+DH=4+a,
∴E(4+a,a),
∴2(2+a)=a(4+a),即a2+3a﹣4=0,
解得:a=1或a=﹣4(舍去),
∴E(5,1),
把F代入反比例解析式得:k=5.
33.(1)解:∵OA=4,
∴A(4,0),
∴当x=4时,y===1,
∴D(4,1);
(2)证明:∵OC=OA=4,
∴E(4,1),
∴CE=AD=1,
在△OCE和△OAD中,
∵,
∴△OCE≌△OAD(SAS),
∴OE=OD
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
