1.1二次函数 课件(共16张PPT)
文档属性
| 名称 | 1.1二次函数 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 901.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-15 00:00:00 | ||
图片预览






文档简介
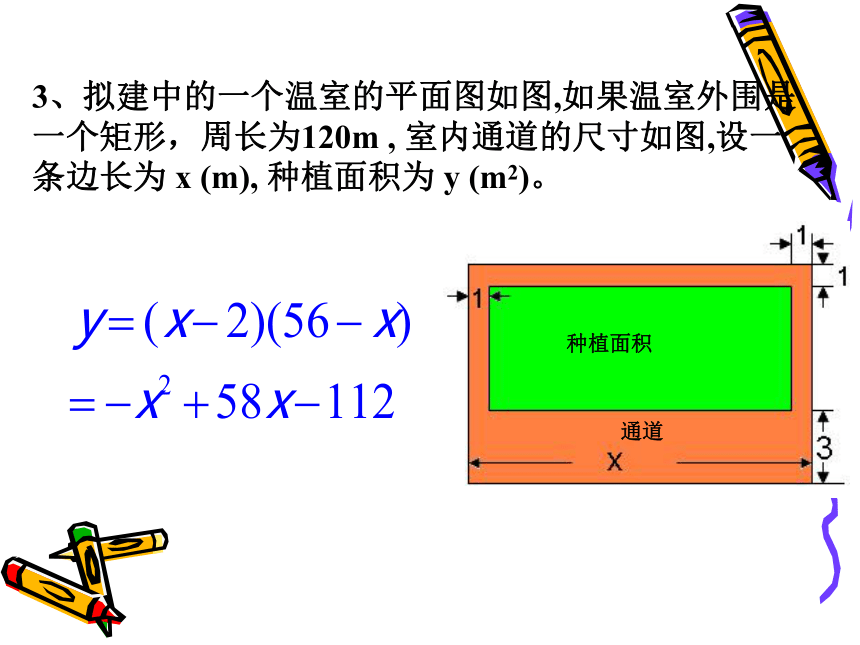
课件16张PPT。1.1 二次函数Q1:我们学过哪些函数?一次函数、正比例函数、反比例函数Q2:函数的定义是什么?在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地确定了一个y的值,那么我们称y是x的函数,其中x是自变量,y是因变量。请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系:1、圆的面积y (cm2)与圆的半径x (cm)。2、王先生存人银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的年利率为x,两年后王先生共得本息y万元。3、拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为120m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2)。上述函数解析式具有哪些共同的特征?经化简后都具有y=ax2+bx+c 的形式。一般的,我们把形如y=ax2+bx+c(其中a,b,c是常数,且a≠0)的函数叫做二次函数。a为二次项系数
b为一次项系数
c为常数项下列函数中,哪些是二次函数?是不是是是先化简后判断
不是做一做二次函数y=ax2+bx+c中a≠0,但b、c可以为0。例1 如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形 (图中阴影部分 ). 设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2) .
求 (1)y关于 x的函数解析式和自变量x的取值范围 ;
(2)当 x分别为0.25,0.5,1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示. 例题探究例1 如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形 (图中阴影部分 ). 设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2) .
求 (1)y关于 x的函数解析式和自变量x的取值范围 ;分析: S四边形EFGH=S正方形ABCD-4×SRt△AEH列表如下: (2)当 x分别为0.25,0.5,1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示. 小结1、图形的面积计算可以采取面积差、面积和、直接计算的方法2、在实际问题中自变量的取值范围需要符合实际作业题6.已知一隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,且矩形的一条边长为2.5m。求:
(1)隧道截面的面积S(m2)与截面上部半圆的半径r(m)之间的函数表达式。
(2)当r=2m时,隧道截面的面积。(精确到0.1m2)例2 已知二次函数y=x2+bx+c, 当x=1时, 函数值为4, 当x=2时, 函数值为-5, 求这个二次函数的解析式.待定系数法2.已知二次函数y=ax2+bx+c, 当x=2时,函数值是3;当x=-2时, 函数值是2;当x=4时, 函数值也是2, 求这个二次函数的表达式. 课内练习小结3、初步形成建立简单二次函数模型的概念,并能根据实际问题确定自变量的取值范围2、用待定系数法求二次函数的解析式
b为一次项系数
c为常数项下列函数中,哪些是二次函数?是不是是是先化简后判断
不是做一做二次函数y=ax2+bx+c中a≠0,但b、c可以为0。例1 如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形 (图中阴影部分 ). 设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2) .
求 (1)y关于 x的函数解析式和自变量x的取值范围 ;
(2)当 x分别为0.25,0.5,1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示. 例题探究例1 如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形 (图中阴影部分 ). 设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2) .
求 (1)y关于 x的函数解析式和自变量x的取值范围 ;分析: S四边形EFGH=S正方形ABCD-4×SRt△AEH列表如下: (2)当 x分别为0.25,0.5,1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示. 小结1、图形的面积计算可以采取面积差、面积和、直接计算的方法2、在实际问题中自变量的取值范围需要符合实际作业题6.已知一隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,且矩形的一条边长为2.5m。求:
(1)隧道截面的面积S(m2)与截面上部半圆的半径r(m)之间的函数表达式。
(2)当r=2m时,隧道截面的面积。(精确到0.1m2)例2 已知二次函数y=x2+bx+c, 当x=1时, 函数值为4, 当x=2时, 函数值为-5, 求这个二次函数的解析式.待定系数法2.已知二次函数y=ax2+bx+c, 当x=2时,函数值是3;当x=-2时, 函数值是2;当x=4时, 函数值也是2, 求这个二次函数的表达式. 课内练习小结3、初步形成建立简单二次函数模型的概念,并能根据实际问题确定自变量的取值范围2、用待定系数法求二次函数的解析式
同课章节目录
