1.4 二次函数的应用(1)同步作业
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.4 二次函数的应用(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A. 2m B. 3m C. 4m D. 5m
2.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
A. y= B. y=﹣ C. y=﹣ D. y=
3.如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
A. 32×20﹣20x﹣30x=540 B. 32×20﹣20x﹣30x﹣x2=540
C. (32﹣x)(20﹣x)=540 D. 32×20﹣20x﹣30x+2x2=540
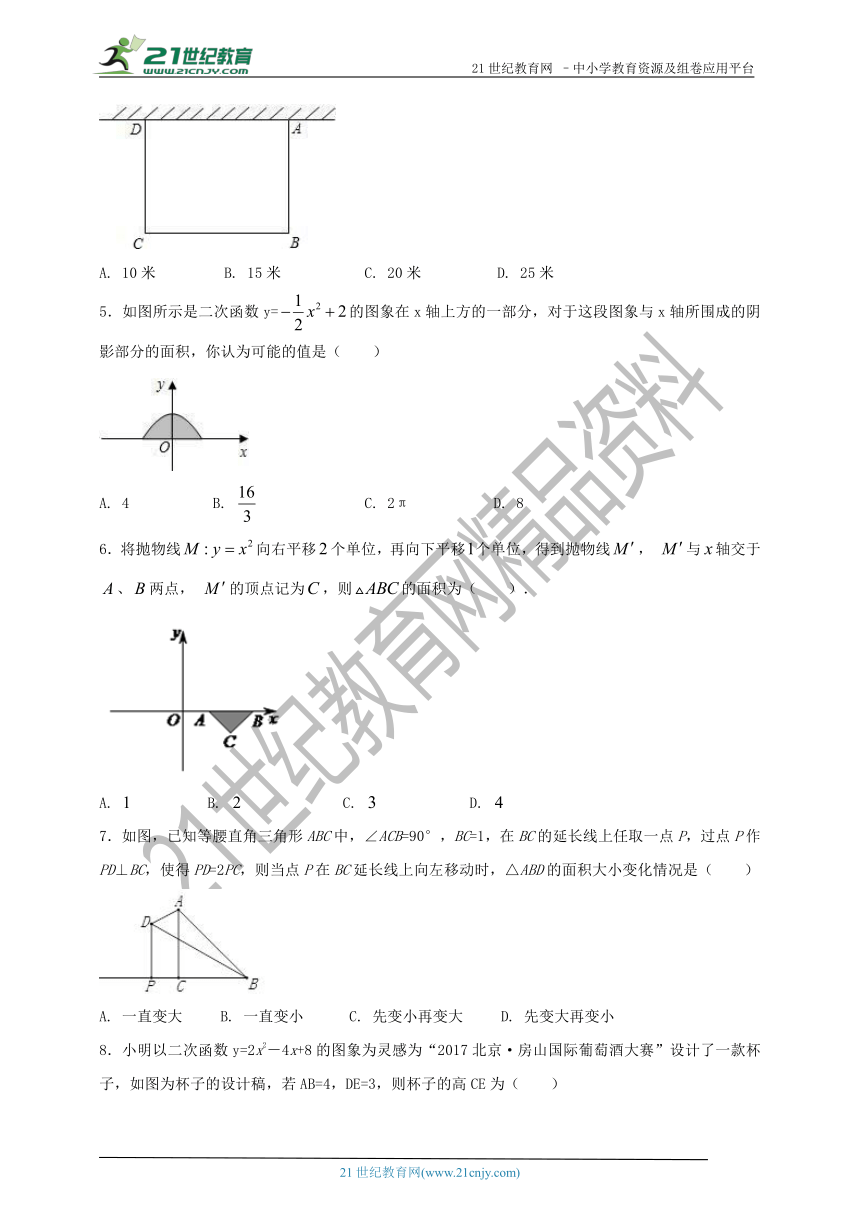
4.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A. 10米 B. 15米 C. 20米 D. 25米
5.如图所示是二次函数y=的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )
A. 4 B. C. 2π D. 8
6.将抛物线向右平移个单位,再向下平移个单位,得到抛物线, 与轴交于、两点, 的顶点记为,则的面积为( ).
A. B. C. D.
7.如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
A. 一直变大 B. 一直变小 C. 先变小再变大 D. 先变大再变小
8.小明以二次函数y=2x2-4x+8的图象为灵感为“2017北京·房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )
A. 14 B. 11 C. 6 D. 3
二、填空题
9.用的铁丝所围的长方形的面积与长的关系__________.
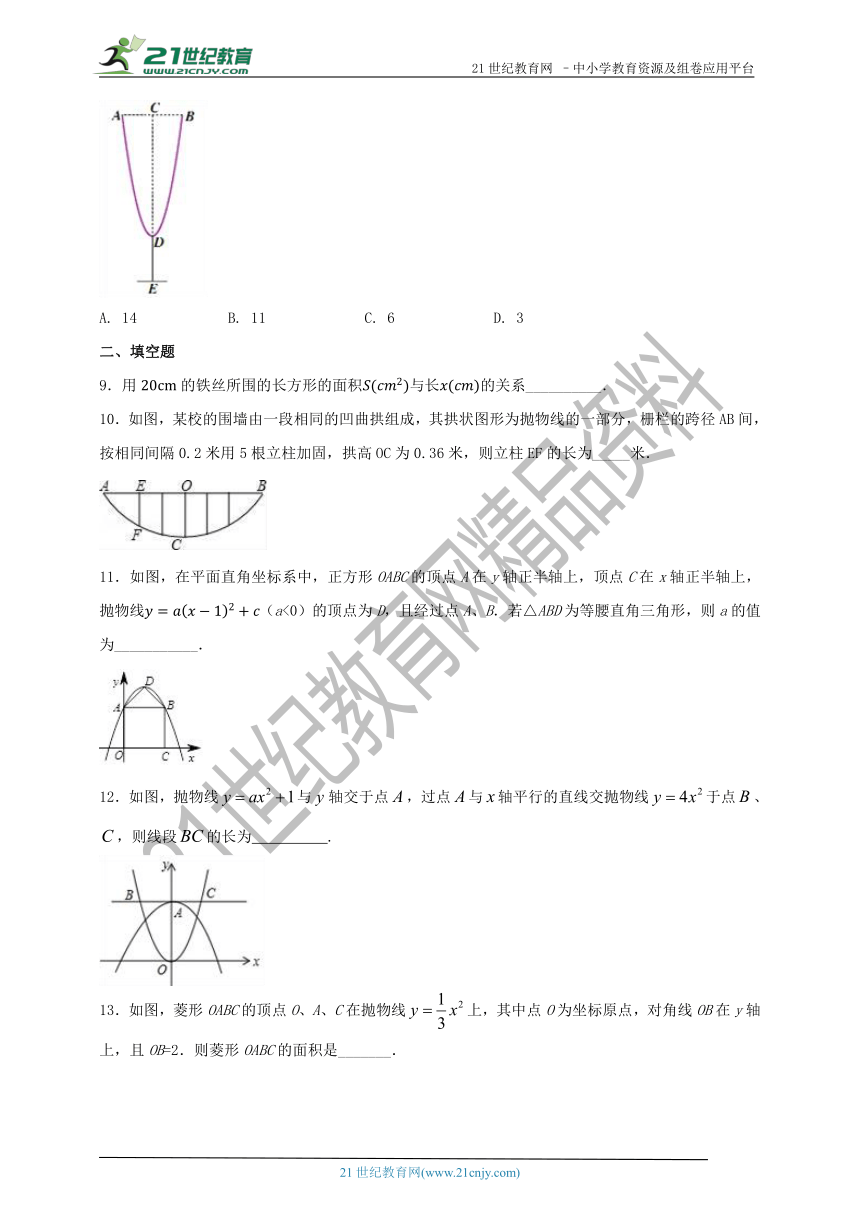
10.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为_____米.
11.如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
12.如图,抛物线与轴交于点,过点与轴平行的直线交抛物线于点、,则线段的长为 .
13.如图,菱形OABC的顶点O、A、C在抛物线上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是_______.
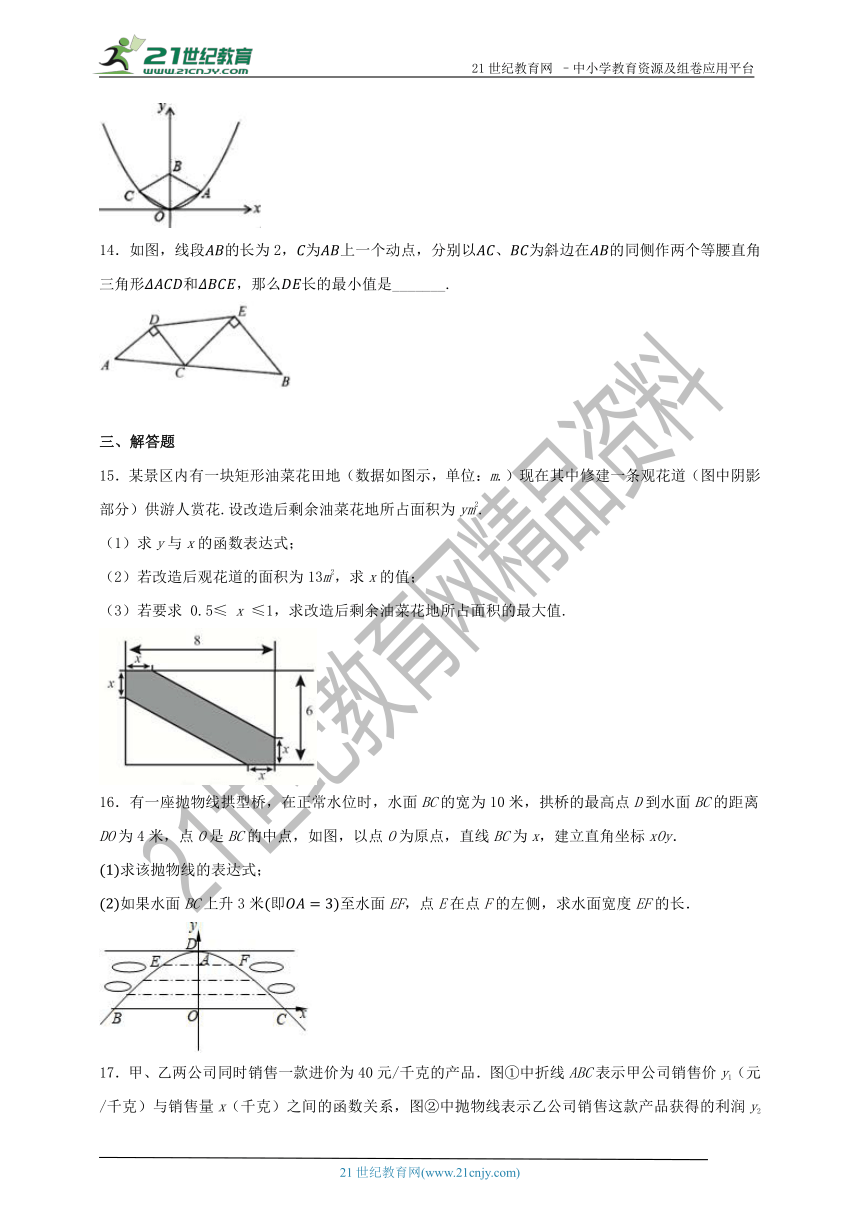
14.如图,线段的长为2,为上一个动点,分别以、为斜边在的同侧作两个等腰直角三角形和,那么长的最小值是_______.
三、解答题
15.某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
16.有一座抛物线拱型桥,在正常水位时,水面BC的宽为10米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x,建立直角坐标xOy.
求该抛物线的表达式;
如果水面BC上升3米即至水面EF,点E在点F的左侧,求水面宽度EF的长.
17.甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
18.河上有一座桥孔为抛物线形的拱桥(如图 ),水面宽 时,水面离桥孔顶部 ,因降暴雨水面上升 .
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ,宽 (横断面如图 所示),暴雨后这艘船能从这座拱桥下通过吗
19.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
参考答案
1.B
【解析】试题解析:设抛物线的解析式为 由题意,得
∴抛物线的解析式为:
当y=0时,
解得: (舍去),
OB=3m.
故选B.
2.C
【解析】如图,由题意可设抛物线的解析式为,
∵由题意可知点A、B的坐标分别为(-5,-4)、(5,-4),且抛物线过点A、B,
∴,解得:,
∴抛物线的解析式为:.
故选C.
3.C
【解析】
如图,将小路平移,则草地的长为(32-x)米,小路的宽为(20-x)米,故可列方程为:
(32﹣x)(20﹣x)=540 .
故选C.
4.A
【解析】设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x= -2x2+40x.
要使矩形ABCD面积最大,
则
即x的长为10m.
故选A.
5.B
【解析】函数与y轴交于(0,2)点,与x轴交于(-2,0)和(2,0)两点,则三点构成的三角形面积S1=4,则以半径为2的半圆的面积为S2=π××22=2π,则阴影部分的面积S有:4<S<2π.因为选项A、C、D均不在S取值范围内.故选 B
6.A
【解析】试题解析:根据题意可得,抛物线的解析式为:
解得:
即
故选A.
点睛:二次函数的平移规律:左加右减,上加下减.
7.C
【解析】试题解析:设PC=x,则PD=2x
∴SΔBPD=×PB×PD= (x+1)×2x=x2+x
SΔABC=×AC×BC= ×1×1=
S梯形ACPD= (2x+1)×x=x2+x
∴SΔABD= S梯形ACPD+ SΔABC- SΔBPD=-x+2
∴△ABD的面积先变小再变大.
故选C.
8.B
【解析】∵,
∴在坐标系中,该二次函数图象的顶点D的坐标为(1,6),
设此时点A、B的坐标分别为,则由题意可知,AB=,而是关于x的一元二次方程的解,
∴,
∴,
又∵AB==4,
∴,解得: ,
∴点A、B的纵坐标为14,
∴DC=14-6=8,
又∵DE=3,
∴CE=DC+DE=11.
故选B.
9.
【解析】试题解析:.
故答案为:
10.0.2
【解析】如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为﹣0.4,
∴当x=﹣0.4时,y=0.16,
∴EF=0.36﹣0.16=0.2米
故答案为0.2.
点睛:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题,熟练掌握待定系数法求函数关系式是解答本题的关键.
11.-1
【解析】分析:抛物线的对称轴方程为即点的横坐标为1,△ABD为等腰直角三角形,则点的横坐标为2,正方形的边长为2,进而求出点的纵坐标为2+1=3,把点代入抛物线解析式,即可求出的值.
详解:抛物线的对称轴方程为
即点的横坐标为1,
△ABD为等腰直角三角形,则点的横坐标为2,正方形的边长为2,
,
代入抛物线解析式得:解得:
故答案为:
点睛:属于二次函数综合体,考查待定系数法求函数解析式,正方形的性质,二次函数的图象与性质等,重点掌握待定系数法.
12.1
【解析】由题意得A(0,1),所以直线BC是y=1,与抛物线联立知,
B(-,1),C(,1),故BC=1.
故答案为1.
13.
【解析】解:∵菱形OABC的顶点O、A、C在抛物线上,对角线OB在y轴上,且OB=2,∴由题意可得:A,C点纵坐标为1,故1=,解得:x=±,故A(,1),C(﹣,1),故菱形OABC的面积是:2×(×2×)=.故答案为: .
点睛:本题主要考查了菱形的性质以及二次函数图象上点的坐标性质,得出A,C点坐标是解题的关键.
14.
【解析】【分析】设AC=x,则BC=2-x,然后分别表示出DC、EC,继而在RT△DCE中,利用勾股定理求出DE长度的表达式,利用函数的知识进行解答即可.
【详解】设AC=x,则BC=2-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=x,CE=(2-x),
∴∠DCE=90°,
故DE2=DC2+CE2=x2+(2-x)2=x2-2x+2=(x-1)2+1,
当x=1时,DE2取得最小值,DE也取得最小值,最小值为1,
故答案为:1.
【点睛】本题考查了二次函数最值及等腰直角三角形,关键是表示出DC、CE,得出DE的表达式.
16.(1) (2)5m
【解析】分析:直接假设出二次函数解析式进而得出答案;
根据题意得出y=3进而求出x的值,即可得出答案.
详解:(1)设抛物线解析式为:,
由题意可得图象经过,,
则,
解得:,
故抛物线解析为:;
由题意可得:时,
解得:,
故EF,
答:水面宽度EF的长为5m.
点睛:此题主要考查了二次函数的应用,正确得出函数解析式是解题关键.
17.(1)y2=―0.4(x―75)2+2250;(2)当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.
【解析】分析:(1)由图象可知y与x之间是一次函数关系,可设y=kx+b,把(0,120),(80,72)代入可得;(2)根据:销售利润W=该产品每千克利润×销售量,列出函数关系式,配成二次函数顶点式,结合自变量取值范围可得其最值.
详解:(1)设y1与x之间的函数表达式为y1=kx+b.
根据题意,当x=0时,y1=120;当x=80时,y1=72.
所以,解得
所以,y1与x之间的函数表达式为y1=-0.6x+120.
设y2与x之间的函数表达式为y2=a(x―75)2+2250,
当x=0时,y2=0,解得a=―0.4.
所以,y2与x之间的函数表达式为y2=―0.4(x―75)2+2250.
(2)解:设甲、乙两公司的销售总利润的差为w(元).
当0<x≤80时,
w=(y1-40)x―y2= (-0.6x+120―40)x-[(-0.4(x―75)2+2250]
=-0.2x2+20x=-0.2(x-50)2+500.
∵-0.2<0,0<x≤80
∴当x=50时, w有最大值,最大值为500.
当80<x≤84时,
w=(72―40)x―[―0.4(x―75)2+2250]=0.4x2―28x,
∵当80<x≤84时,w随x的增大而增大,
∴当x=84时, 有最大值,最大值为470.4.
综上所述,当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.
点睛:本题考查了一次函数和二次函数的应用,涉及了待定系数法求函数解析式的知识 ,解答本题的关键是根据图象找出图象中所包含的有用信息.
18.(1)水面宽为 米;(2)这艘船能从这座拱桥下通过.
【解析】试题分析:
(1)建立如下图所示的平面直角坐标系,由题意设抛物线型拱桥的解析式为:y=ax2,由题意可知此抛物线过点(3,-3),由此即可求出抛物线的解析式,把y=-2代入所得解析式,解此对应的x的值,即可求得此时水面的宽;
(2)由题意在(1)中所得的解析式中,求出当x=2时对应的y的值,比较此时y的值的绝对值和1.5的大小即可得出结论.
试题解析:
(1) 如图,以抛物线的顶点为原点,以桥面为 轴,建立平面直角坐标系,由题意可知抛物线过点 ,
设抛物线的函数表达式为: .
把 代入 ,可求 ,
则抛物线对应的函数表达式为 .
当水面上涨 米后,水面所在的位置为直线 ,
令 得,则,解得: , ,
∴此时水面宽为为: (米);
(2)由题意 :当船在桥拱的正中心航行时,船的边缘距抛物线对称轴水平距离为 米,在中,令 得, ,
∵船上货物最高点距拱顶为: (米)且 ,
∴这艘船能从这座拱桥下通过.
19.(1)y=﹣0.5x2+0.5;(2)所需不锈钢管的总长度为80米.
【解析】试题分析:(1)根据所建坐标系特点可设解析式为y=ax2+c的形式,结合图象易求B点和C点坐标,代入解析式解方程组求出a,c的值得解析式;
(2)根据对称性求B3、B4的纵坐标后再求出总长度.
试题解析:(1)由题意得B(0,0.5)、C(1,0)
设抛物线的解析式为:y=ax2+c
代入得a=﹣0.5,c=0.5,
故解析式为y=﹣0.5x2+0.5;
(2)如图1所示:
∵当x=0.2时,y=0.48,
当x=0.6时,y=0.32,
∴B1C1+B2C2+B3C3+B4C4=2×(0.48+0.32)=1.6米
∴所需不锈钢管的总长度为:1.6×50=80米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.4 二次函数的应用(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A. 2m B. 3m C. 4m D. 5m
2.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
A. y= B. y=﹣ C. y=﹣ D. y=
3.如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
A. 32×20﹣20x﹣30x=540 B. 32×20﹣20x﹣30x﹣x2=540
C. (32﹣x)(20﹣x)=540 D. 32×20﹣20x﹣30x+2x2=540
4.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A. 10米 B. 15米 C. 20米 D. 25米
5.如图所示是二次函数y=的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )
A. 4 B. C. 2π D. 8
6.将抛物线向右平移个单位,再向下平移个单位,得到抛物线, 与轴交于、两点, 的顶点记为,则的面积为( ).
A. B. C. D.
7.如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
A. 一直变大 B. 一直变小 C. 先变小再变大 D. 先变大再变小
8.小明以二次函数y=2x2-4x+8的图象为灵感为“2017北京·房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )
A. 14 B. 11 C. 6 D. 3
二、填空题
9.用的铁丝所围的长方形的面积与长的关系__________.
10.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为_____米.
11.如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
12.如图,抛物线与轴交于点,过点与轴平行的直线交抛物线于点、,则线段的长为 .
13.如图,菱形OABC的顶点O、A、C在抛物线上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是_______.
14.如图,线段的长为2,为上一个动点,分别以、为斜边在的同侧作两个等腰直角三角形和,那么长的最小值是_______.
三、解答题
15.某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
16.有一座抛物线拱型桥,在正常水位时,水面BC的宽为10米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x,建立直角坐标xOy.
求该抛物线的表达式;
如果水面BC上升3米即至水面EF,点E在点F的左侧,求水面宽度EF的长.
17.甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
18.河上有一座桥孔为抛物线形的拱桥(如图 ),水面宽 时,水面离桥孔顶部 ,因降暴雨水面上升 .
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ,宽 (横断面如图 所示),暴雨后这艘船能从这座拱桥下通过吗
19.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
参考答案
1.B
【解析】试题解析:设抛物线的解析式为 由题意,得
∴抛物线的解析式为:
当y=0时,
解得: (舍去),
OB=3m.
故选B.
2.C
【解析】如图,由题意可设抛物线的解析式为,
∵由题意可知点A、B的坐标分别为(-5,-4)、(5,-4),且抛物线过点A、B,
∴,解得:,
∴抛物线的解析式为:.
故选C.
3.C
【解析】
如图,将小路平移,则草地的长为(32-x)米,小路的宽为(20-x)米,故可列方程为:
(32﹣x)(20﹣x)=540 .
故选C.
4.A
【解析】设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x= -2x2+40x.
要使矩形ABCD面积最大,
则
即x的长为10m.
故选A.
5.B
【解析】函数与y轴交于(0,2)点,与x轴交于(-2,0)和(2,0)两点,则三点构成的三角形面积S1=4,则以半径为2的半圆的面积为S2=π××22=2π,则阴影部分的面积S有:4<S<2π.因为选项A、C、D均不在S取值范围内.故选 B
6.A
【解析】试题解析:根据题意可得,抛物线的解析式为:
解得:
即
故选A.
点睛:二次函数的平移规律:左加右减,上加下减.
7.C
【解析】试题解析:设PC=x,则PD=2x
∴SΔBPD=×PB×PD= (x+1)×2x=x2+x
SΔABC=×AC×BC= ×1×1=
S梯形ACPD= (2x+1)×x=x2+x
∴SΔABD= S梯形ACPD+ SΔABC- SΔBPD=-x+2
∴△ABD的面积先变小再变大.
故选C.
8.B
【解析】∵,
∴在坐标系中,该二次函数图象的顶点D的坐标为(1,6),
设此时点A、B的坐标分别为,则由题意可知,AB=,而是关于x的一元二次方程的解,
∴,
∴,
又∵AB==4,
∴,解得: ,
∴点A、B的纵坐标为14,
∴DC=14-6=8,
又∵DE=3,
∴CE=DC+DE=11.
故选B.
9.
【解析】试题解析:.
故答案为:
10.0.2
【解析】如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为﹣0.4,
∴当x=﹣0.4时,y=0.16,
∴EF=0.36﹣0.16=0.2米
故答案为0.2.
点睛:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题,熟练掌握待定系数法求函数关系式是解答本题的关键.
11.-1
【解析】分析:抛物线的对称轴方程为即点的横坐标为1,△ABD为等腰直角三角形,则点的横坐标为2,正方形的边长为2,进而求出点的纵坐标为2+1=3,把点代入抛物线解析式,即可求出的值.
详解:抛物线的对称轴方程为
即点的横坐标为1,
△ABD为等腰直角三角形,则点的横坐标为2,正方形的边长为2,
,
代入抛物线解析式得:解得:
故答案为:
点睛:属于二次函数综合体,考查待定系数法求函数解析式,正方形的性质,二次函数的图象与性质等,重点掌握待定系数法.
12.1
【解析】由题意得A(0,1),所以直线BC是y=1,与抛物线联立知,
B(-,1),C(,1),故BC=1.
故答案为1.
13.
【解析】解:∵菱形OABC的顶点O、A、C在抛物线上,对角线OB在y轴上,且OB=2,∴由题意可得:A,C点纵坐标为1,故1=,解得:x=±,故A(,1),C(﹣,1),故菱形OABC的面积是:2×(×2×)=.故答案为: .
点睛:本题主要考查了菱形的性质以及二次函数图象上点的坐标性质,得出A,C点坐标是解题的关键.
14.
【解析】【分析】设AC=x,则BC=2-x,然后分别表示出DC、EC,继而在RT△DCE中,利用勾股定理求出DE长度的表达式,利用函数的知识进行解答即可.
【详解】设AC=x,则BC=2-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=x,CE=(2-x),
∴∠DCE=90°,
故DE2=DC2+CE2=x2+(2-x)2=x2-2x+2=(x-1)2+1,
当x=1时,DE2取得最小值,DE也取得最小值,最小值为1,
故答案为:1.
【点睛】本题考查了二次函数最值及等腰直角三角形,关键是表示出DC、CE,得出DE的表达式.
16.(1) (2)5m
【解析】分析:直接假设出二次函数解析式进而得出答案;
根据题意得出y=3进而求出x的值,即可得出答案.
详解:(1)设抛物线解析式为:,
由题意可得图象经过,,
则,
解得:,
故抛物线解析为:;
由题意可得:时,
解得:,
故EF,
答:水面宽度EF的长为5m.
点睛:此题主要考查了二次函数的应用,正确得出函数解析式是解题关键.
17.(1)y2=―0.4(x―75)2+2250;(2)当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.
【解析】分析:(1)由图象可知y与x之间是一次函数关系,可设y=kx+b,把(0,120),(80,72)代入可得;(2)根据:销售利润W=该产品每千克利润×销售量,列出函数关系式,配成二次函数顶点式,结合自变量取值范围可得其最值.
详解:(1)设y1与x之间的函数表达式为y1=kx+b.
根据题意,当x=0时,y1=120;当x=80时,y1=72.
所以,解得
所以,y1与x之间的函数表达式为y1=-0.6x+120.
设y2与x之间的函数表达式为y2=a(x―75)2+2250,
当x=0时,y2=0,解得a=―0.4.
所以,y2与x之间的函数表达式为y2=―0.4(x―75)2+2250.
(2)解:设甲、乙两公司的销售总利润的差为w(元).
当0<x≤80时,
w=(y1-40)x―y2= (-0.6x+120―40)x-[(-0.4(x―75)2+2250]
=-0.2x2+20x=-0.2(x-50)2+500.
∵-0.2<0,0<x≤80
∴当x=50时, w有最大值,最大值为500.
当80<x≤84时,
w=(72―40)x―[―0.4(x―75)2+2250]=0.4x2―28x,
∵当80<x≤84时,w随x的增大而增大,
∴当x=84时, 有最大值,最大值为470.4.
综上所述,当销售量为50千克时,甲乙两公司获得的利润的差最大,最大是500元.
点睛:本题考查了一次函数和二次函数的应用,涉及了待定系数法求函数解析式的知识 ,解答本题的关键是根据图象找出图象中所包含的有用信息.
18.(1)水面宽为 米;(2)这艘船能从这座拱桥下通过.
【解析】试题分析:
(1)建立如下图所示的平面直角坐标系,由题意设抛物线型拱桥的解析式为:y=ax2,由题意可知此抛物线过点(3,-3),由此即可求出抛物线的解析式,把y=-2代入所得解析式,解此对应的x的值,即可求得此时水面的宽;
(2)由题意在(1)中所得的解析式中,求出当x=2时对应的y的值,比较此时y的值的绝对值和1.5的大小即可得出结论.
试题解析:
(1) 如图,以抛物线的顶点为原点,以桥面为 轴,建立平面直角坐标系,由题意可知抛物线过点 ,
设抛物线的函数表达式为: .
把 代入 ,可求 ,
则抛物线对应的函数表达式为 .
当水面上涨 米后,水面所在的位置为直线 ,
令 得,则,解得: , ,
∴此时水面宽为为: (米);
(2)由题意 :当船在桥拱的正中心航行时,船的边缘距抛物线对称轴水平距离为 米,在中,令 得, ,
∵船上货物最高点距拱顶为: (米)且 ,
∴这艘船能从这座拱桥下通过.
19.(1)y=﹣0.5x2+0.5;(2)所需不锈钢管的总长度为80米.
【解析】试题分析:(1)根据所建坐标系特点可设解析式为y=ax2+c的形式,结合图象易求B点和C点坐标,代入解析式解方程组求出a,c的值得解析式;
(2)根据对称性求B3、B4的纵坐标后再求出总长度.
试题解析:(1)由题意得B(0,0.5)、C(1,0)
设抛物线的解析式为:y=ax2+c
代入得a=﹣0.5,c=0.5,
故解析式为y=﹣0.5x2+0.5;
(2)如图1所示:
∵当x=0.2时,y=0.48,
当x=0.6时,y=0.32,
∴B1C1+B2C2+B3C3+B4C4=2×(0.48+0.32)=1.6米
∴所需不锈钢管的总长度为:1.6×50=80米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
