九年级数学上册第二章简单事件的概率微专题概率与代数、几何的综合随堂练习(含解析)
文档属性
| 名称 | 九年级数学上册第二章简单事件的概率微专题概率与代数、几何的综合随堂练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-19 00:00:00 | ||
图片预览


文档简介
概率与代数、几何的综合_
一 概率与代数式的综合
(教材P59作业题第2题)
下表是中国人民银行公布的中国人寿保险经验生命表(2000~2003年)女性表的部分摘录.根据下表估算下列概率(结果精确到0.000 1).
年龄x
生存人数lx
死亡人数dx
0
1 000 000
661
1
999 339
536
30
991 476
403
31
991 074
428
61
938 005
6 064
62
931 941
6 743
63
925 198
7 489
64
917 709
8 314
79
649 175
32 429
80
616 746
34 398
81
582 347
36 253
82
546 095
37 950
(1)一名女性79岁当年死亡的概率;
(2)一名61岁的女性活到80岁的概率.
解:(1)一名女性79岁当年死亡的概率P==≈0.050 0;
(2)一名61岁的女性活到80岁的概率P=≈0.657 5.
【思想方法】 概率与代数、几何的综合运用其本质还是求概率,只不过应用代数和几何的方法确定某些限制条件的事件数.一般的方法是先利用列表或画树状图求出所有等可能的情况,然后求出满足所涉及知识的情形,再求概率,此类问题能很好地考查概率与其他知识的综合运用.
[2016·滨州]有5张看上去无差别的卡片,上面分别写着0,π,,,1.333,随机抽取1张,则取出的数是无理数的概率是____.
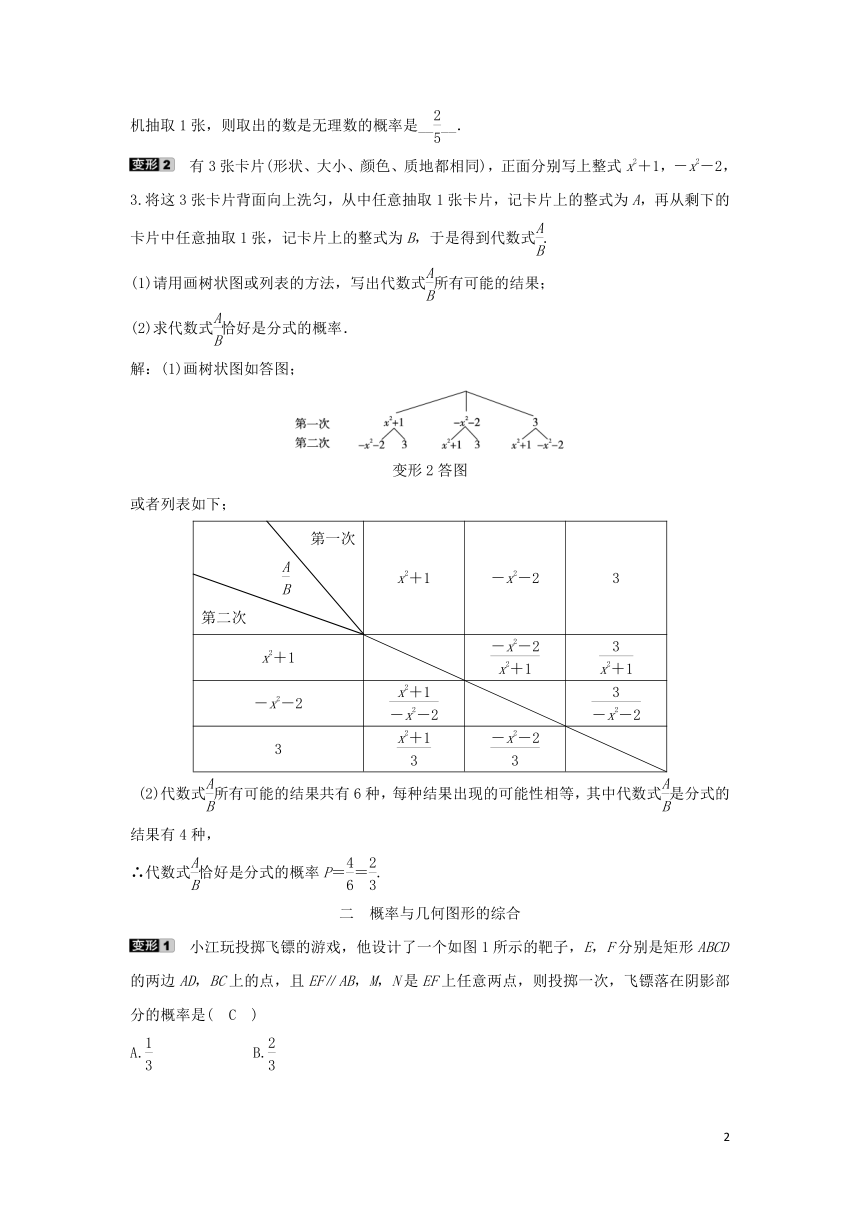
有3张卡片(形状、大小、颜色、质地都相同),正面分别写上整式x2+1,-x2-2,3.将这3张卡片背面向上洗匀,从中任意抽取1张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取1张,记卡片上的整式为B,于是得到代数式.
(1)请用画树状图或列表的方法,写出代数式所有可能的结果;
(2)求代数式恰好是分式的概率.
解:(1)画树状图如答图;
变形2答图
或者列表如下;
第一次
第二次
x2+1
-x2-2
3
x2+1
-x2-2
3
(2)代数式所有可能的结果共有6种,每种结果出现的可能性相等,其中代数式是分式的结果有4种,
∴代数式恰好是分式的概率P==.
二 概率与几何图形的综合
小江玩投掷飞镖的游戏,他设计了一个如图1所示的靶子,E,F分别是矩形ABCD的两边AD,BC上的点,且EF∥AB,M,N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率是( C )
A. B.
C. D.
图1 图2
如图2,有以下3个条件:①AC=AB;②AB∥CD;③∠1=∠2,从这3个条件中选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( D )
A.0 B. C. D.1
如图3,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是__△DFG或△DHF__(只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,求所画三角形与△ABC面积相等的概率(用画树状图或列表法求解).
图3
解:(2)画树状图如答图.
变形3答图
由树状图可知共有6种等可能结果,其中与△ABC面积相等的有3种,即△DHF,△DGF和△EGF,
∴所画三角形与△ABC面积相等的概率P==.
三 概率与方程(或不等式)的综合
有 9 张卡片,分别写有 1~9 这九个数字,将它们背面朝上洗匀后,任意抽出1张,记卡片上的数字为 a,则使关于 x 的不等式组 有解的概率为____.
【解析】 设不等式组有解,则不等式组 的解为3≤x<,那么必须满足条件>3?a>5,∴满足条件的a的值为6,7,8,9,∴有解的概率P=.
大课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值;然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数解的概率.
解:(1)列表表示(p,q)所有可能的结果如下,共有9种;
q
(p,q)
p
-1
0
1
-1
(-1,-1)
(-1,0)
(-1,1)
0
(0,-1)
(0,0)
(0,1)
1
(1,-1)
(1,0)
(1,1)
(2)当p2-4q<0时,方程没有实数解,满足p2-4q<0的(p,q)共有3对:(-1,1),(0,1),(1,1),
∴关于x的方程x2+px+q=0没有实数解的概率P==.
四 概率与平面直角坐标系的综合
[2017·湘潭]从-2,1,3这三个数中任取两个不同的数,作为点的坐标.
(1)写出该点所有可能的坐标;
(2)求该点在第一象限的概率.
解: (1)画树状图如答图,
变形1答图
∴所有可能的坐标为(1,3),(1,-2),(3,1),(3,-2),(-2,1),(-2,3);
(2)∵共有6种等可能的结果,其中点(1,3),(3,1)落在第一象限,
∴该点刚好落在第一象限的概率为=.
五 概率与反比例函数的综合
[2016·甘肃]在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字-1,-2,0.现从甲袋中任意摸出1个小球,记其标有的数字为x,再从乙袋中任意摸出1个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M的所有可能的坐标;
(2)求点M(x,y)在函数y=-的图象上的概率.
解:(1)列表如下;
x
y
-1
-2
0
0
(0,-1)
(0,-2)
(0,0)
1
(1,-1)
(1,-2)
(1,0)
2
(2,-1)
(2,-2)
(2,0)
(2)由上表可知,点M的坐标共有9种可能的结果,每种结果出现的可能性相等,其中在函数y=-的图象上(记为事件A)的点M有2种,即(1,-2)和(2,-1),
∴所求概率P(A)=.
六 概率与一次函数的综合
在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
解:(1)画树状图如答图,
变形1答图
则点Q所有可能的坐标为(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种;
(2)∵共有12种等可能的结果,其中在函数y=-x+5的图象上的有4种:(1,4),(2,3),(3,2),(4,1),
∴点(x,y)在函数y=-x+5的图象上的概率为=;
(3)这个游戏不公平.
理由:∵x,y满足xy>6有(2,4),(3,4),(4,2),(4,3),共4种情况,x,y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1),共6种情况.
∴P(小明胜)==,
P(小红胜)==,
∴这个游戏不公平.
公平的游戏规则:若x,y满足xy≥6则小明胜,若x,y满足xy<6则小红胜.
一 概率与代数式的综合
(教材P59作业题第2题)
下表是中国人民银行公布的中国人寿保险经验生命表(2000~2003年)女性表的部分摘录.根据下表估算下列概率(结果精确到0.000 1).
年龄x
生存人数lx
死亡人数dx
0
1 000 000
661
1
999 339
536
30
991 476
403
31
991 074
428
61
938 005
6 064
62
931 941
6 743
63
925 198
7 489
64
917 709
8 314
79
649 175
32 429
80
616 746
34 398
81
582 347
36 253
82
546 095
37 950
(1)一名女性79岁当年死亡的概率;
(2)一名61岁的女性活到80岁的概率.
解:(1)一名女性79岁当年死亡的概率P==≈0.050 0;
(2)一名61岁的女性活到80岁的概率P=≈0.657 5.
【思想方法】 概率与代数、几何的综合运用其本质还是求概率,只不过应用代数和几何的方法确定某些限制条件的事件数.一般的方法是先利用列表或画树状图求出所有等可能的情况,然后求出满足所涉及知识的情形,再求概率,此类问题能很好地考查概率与其他知识的综合运用.
[2016·滨州]有5张看上去无差别的卡片,上面分别写着0,π,,,1.333,随机抽取1张,则取出的数是无理数的概率是____.
有3张卡片(形状、大小、颜色、质地都相同),正面分别写上整式x2+1,-x2-2,3.将这3张卡片背面向上洗匀,从中任意抽取1张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取1张,记卡片上的整式为B,于是得到代数式.
(1)请用画树状图或列表的方法,写出代数式所有可能的结果;
(2)求代数式恰好是分式的概率.
解:(1)画树状图如答图;
变形2答图
或者列表如下;
第一次
第二次
x2+1
-x2-2
3
x2+1
-x2-2
3
(2)代数式所有可能的结果共有6种,每种结果出现的可能性相等,其中代数式是分式的结果有4种,
∴代数式恰好是分式的概率P==.
二 概率与几何图形的综合
小江玩投掷飞镖的游戏,他设计了一个如图1所示的靶子,E,F分别是矩形ABCD的两边AD,BC上的点,且EF∥AB,M,N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率是( C )
A. B.
C. D.
图1 图2
如图2,有以下3个条件:①AC=AB;②AB∥CD;③∠1=∠2,从这3个条件中选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( D )
A.0 B. C. D.1
如图3,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是__△DFG或△DHF__(只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,求所画三角形与△ABC面积相等的概率(用画树状图或列表法求解).
图3
解:(2)画树状图如答图.
变形3答图
由树状图可知共有6种等可能结果,其中与△ABC面积相等的有3种,即△DHF,△DGF和△EGF,
∴所画三角形与△ABC面积相等的概率P==.
三 概率与方程(或不等式)的综合
有 9 张卡片,分别写有 1~9 这九个数字,将它们背面朝上洗匀后,任意抽出1张,记卡片上的数字为 a,则使关于 x 的不等式组 有解的概率为____.
【解析】 设不等式组有解,则不等式组 的解为3≤x<,那么必须满足条件>3?a>5,∴满足条件的a的值为6,7,8,9,∴有解的概率P=.
大课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值;然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数解的概率.
解:(1)列表表示(p,q)所有可能的结果如下,共有9种;
q
(p,q)
p
-1
0
1
-1
(-1,-1)
(-1,0)
(-1,1)
0
(0,-1)
(0,0)
(0,1)
1
(1,-1)
(1,0)
(1,1)
(2)当p2-4q<0时,方程没有实数解,满足p2-4q<0的(p,q)共有3对:(-1,1),(0,1),(1,1),
∴关于x的方程x2+px+q=0没有实数解的概率P==.
四 概率与平面直角坐标系的综合
[2017·湘潭]从-2,1,3这三个数中任取两个不同的数,作为点的坐标.
(1)写出该点所有可能的坐标;
(2)求该点在第一象限的概率.
解: (1)画树状图如答图,
变形1答图
∴所有可能的坐标为(1,3),(1,-2),(3,1),(3,-2),(-2,1),(-2,3);
(2)∵共有6种等可能的结果,其中点(1,3),(3,1)落在第一象限,
∴该点刚好落在第一象限的概率为=.
五 概率与反比例函数的综合
[2016·甘肃]在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字-1,-2,0.现从甲袋中任意摸出1个小球,记其标有的数字为x,再从乙袋中任意摸出1个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M的所有可能的坐标;
(2)求点M(x,y)在函数y=-的图象上的概率.
解:(1)列表如下;
x
y
-1
-2
0
0
(0,-1)
(0,-2)
(0,0)
1
(1,-1)
(1,-2)
(1,0)
2
(2,-1)
(2,-2)
(2,0)
(2)由上表可知,点M的坐标共有9种可能的结果,每种结果出现的可能性相等,其中在函数y=-的图象上(记为事件A)的点M有2种,即(1,-2)和(2,-1),
∴所求概率P(A)=.
六 概率与一次函数的综合
在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
解:(1)画树状图如答图,
变形1答图
则点Q所有可能的坐标为(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种;
(2)∵共有12种等可能的结果,其中在函数y=-x+5的图象上的有4种:(1,4),(2,3),(3,2),(4,1),
∴点(x,y)在函数y=-x+5的图象上的概率为=;
(3)这个游戏不公平.
理由:∵x,y满足xy>6有(2,4),(3,4),(4,2),(4,3),共4种情况,x,y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1),共6种情况.
∴P(小明胜)==,
P(小红胜)==,
∴这个游戏不公平.
公平的游戏规则:若x,y满足xy≥6则小明胜,若x,y满足xy<6则小红胜.
同课章节目录
