3.2图形的旋转随堂练习（含解析）

3.2__图形的旋转
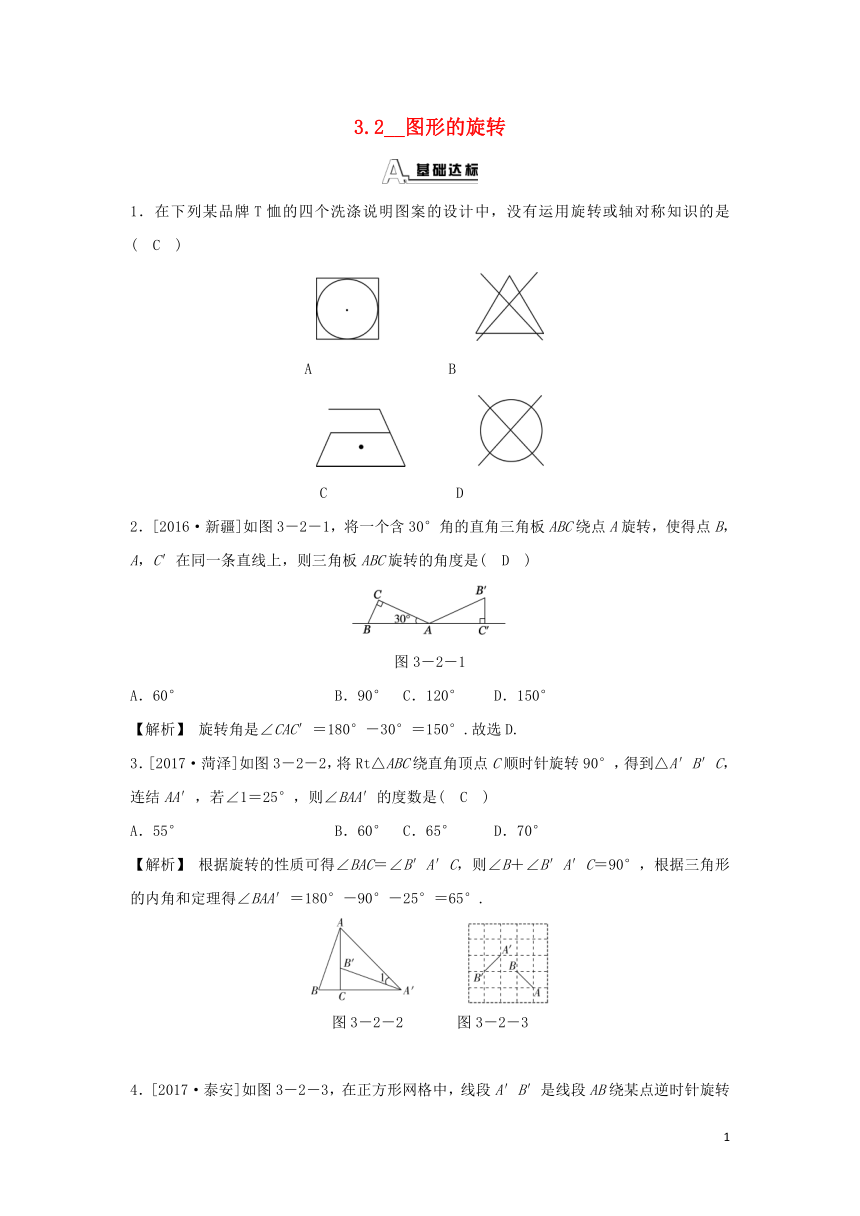
1．在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用旋转或轴对称知识的是(　C　)
　　　　　 A　　　　　 　　　B
　　　　　 C　　　　　 　　　D
2．[2016·新疆]如图3－2－1，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的角度是(　D　)
图3－2－1
A．60° B．90° C．120° D．150°
【解析】 旋转角是∠CAC′＝180°－30°＝150°.故选D.
3．[2017·菏泽]如图3－2－2，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠1＝25°，则∠BAA′的度数是(　C　)
A．55° B．60° C．65° D．70°
【解析】 根据旋转的性质可得∠BAC＝∠B′A′C，则∠B＋∠B′A′C＝90°，根据三角形的内角和定理得∠BAA′＝180°－90°－25°＝65°.

图3－2－2　 图3－2－3
4．[2017·泰安]如图3－2－3，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为(　C　)
A．30° B．60° C．90° D．120°
【解析】 AA′和BB′的垂直平分线的交点即为旋转中心O，根据网格的特征可知 ∠AOA′＝90°，所以旋转角 α＝90°.
5．[2017·天津]如图3－2－4，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点恰好落在AB的延长线上，连结AD.下列结论一定正确的是(　C　)
图3－2－4
A．∠ABD＝∠E B．∠CBE＝∠C
C．AD∥BC D．AD＝BC
【解析】 根据旋转的性质，可得AB＝DB，CB＝EB，∠ABD＝∠CBE＝60°，∴△ABD是等边三角形，∴∠DAB＝∠CBE＝60°，根据“同位角相等，两直线平行”可得AD∥BC，故选C.
6．如图3－2－5，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为(　C　)
图3－2－5
A．35° B．40° C．50° D．65°
7．[2017·宜宾]如图3－2－6，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB＝15°，则∠AOD的度数是__60°__.
图3－2－6
【解析】 由旋转可知∠BOD＝45°，∵∠AOB＝15°，∴∠AOD＝60°.
8．如图3－2－7，在△ABC和△ADE中，点E在BC边上，∠BAC＝∠DAE，∠B＝∠D，AB＝AD.
(1)求证：△ABC≌△ADE；
(2)如果∠AEC＝75°，将△ADE绕着点A旋转一个锐角后与△ABC重合，求这个旋转角的大小．
图3－2－7
解：(1)证明：∵∠BAC＝∠DAE，AB＝AD，∠B＝∠D，
∴△ABC≌△ADE(ASA)；
(2)∵△ABC≌△ADE，
∴AC与AE是一组对应边，
∴∠CAE为旋转角．
∵AE＝AC，∠AEC＝75°，
∴∠ACE＝∠AEC＝75°，
∴∠CAE＝180°－75°－75°＝30°.
9．如图3－2－8，在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，△A′B′C是由△ABC绕C点顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连结AB′，且A，B′，A′在同一条直线上，则AA′的长为(　A　)
图3－2－8
A．6 B．4
C．3 D．3
【解析】 ∵在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，
∴∠CAB＝30°，AB＝4.
由旋转性质，得AB＝A′B′＝4，AC＝A′C，∠A′＝∠CAB＝30°，∠A′B′C＝∠B＝60°，B′C＝BC＝2，
∴∠CAA′＝∠A′＝30°，
∵∠A′B′C＝∠ACB′＋∠B′AC，
∴∠ACB′＝∠B′AC＝30°，∴AB′＝B′C＝2，
∴AA′＝AB′＋A′B′＝2＋4＝6.故选A.
10．[2016·西宁]如图3－2－9，已知正方形ABCD的边长为3，E，F分别是AB，BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM.若AE＝1，则FM的长为____．
图3－2－9
【解析】 ∵△DAE逆时针旋转90°得到△DCM，
∴∠FCM＝∠FCD＋∠DCM＝180°，
∴F，C，M三点共线，
∴DE＝DM，∠EDM＝90°，
∴∠EDF＋∠FDM＝90°，∵∠EDF＝45°，
∴∠FDM＝∠EDF＝45°，
在△DEF和△DMF中，
∴△DEF≌△DMF(SAS)，∴EF＝MF，
设EF＝MF＝x，
∵AE＝CM＝1，且BC＝3，
∴BM＝BC＋CM＝3＋1＝4，
∴BF＝BM－MF＝BM－EF＝4－x，
∵EB＝AB－AE＝3－1＝2，
在Rt△EBF中，由勾股定理，得EB2＋BF2＝EF2，
即22＋(4－x)2＝x2，
解得x＝，∴FM＝.
11．[2017·宁波]在4×4的方格纸中，△ABC的三个顶点都在格点上．
(1)在图3－2－10①中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可)；
(2)将图②中的△ABC绕着点C按顺时针方向旋转90°，画出经旋转后的三角形．
图3－2－10
解： (1)如答图①所示；(画出其中一种情况即可)
第11题答图①
(2)如答图②所示．
第11题答图②
12．[2016·日照]如图3－2－11，在正方形ABCD中，E，F是对角线BD上两点，且∠EAF＝45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连结EQ，求证：
图
3－2－11
(1)EA是∠QED的平分线；
(2)EF2＝BE2＋DF2.
证明：(1)∵将△ADF绕点A顺时针旋转90°后，得到△ABQ，
∴BQ＝DF，AQ＝AF，∠ABQ＝∠ADF＝45°，∠QAF＝90°，
∵∠EAF＝45°，∴∠QAE＝45°.
在△AQE和△AFE中，
∴△AQE≌△AFE(SAS)，∴∠AEQ＝∠AEF，
∴EA是∠QED的平分线；
(2)由(1)得△AQE≌△AFE，∴QE＝EF，
在Rt△QBE中，BQ2＋BE2＝QE2，
则EF2＝BE2＋DF2.
13．如图3－2－12，在△ABC中，AB＝AC，∠BAC＝α(0°<α<60°)，将线段BC绕点B逆时针旋转60°得到线段BD.
图3－2－12
(1)如图①，直接写出∠ABD的大小(用含α的式子表示)；
(2)如图②，∠BCE＝150°，∠ABE＝60°，判断△ABE的形状并加以证明；
(3)在(2)的条件下，连结DE，若∠DEC＝45°，求α的值．
解：(1)30°－α；
(2)△ABE为等边三角形．
证明：如答图，连结AD，CD，ED.
∵线段BC绕点B逆时针旋转60°得到线段BD，
∴BC＝BD，∠DBC＝60°.又∵∠ABE＝60°，
∴∠ABD＝60°－∠DBE＝∠EBC＝30°－α，
第13题答图
且△BCD为等边三角形，
在△ABD与△ACD中，
∴△ABD≌△ACD(SSS)，
∴∠BAD＝∠CAD＝∠BAC＝α.
∵∠BCE＝150°，
∴∠BEC＝180°－－150°＝α，
∴∠BAD＝∠BEC.
在△ABD与△EBC中，
∴△ABD≌△EBC(AAS)，∴AB＝BE.
又∵∠ABE＝60°，∴△ABE为等边三角形；
(3)∵∠BCD＝60°，∠BCE＝150°，
∴∠DCE＝150°－60°＝90°.又∵∠DEC＝45°，
∴△DCE为等腰直角三角形，
∴DC＝CE＝BC，
∴∠EBC＝＝15°，
∵∠EBC＝30°－α＝15°，∴α＝30°.