1.1 .1三角形的定义、三角形的分类、三角形的稳定性 同步作业
文档属性
| 名称 | 1.1 .1三角形的定义、三角形的分类、三角形的稳定性 同步作业 | 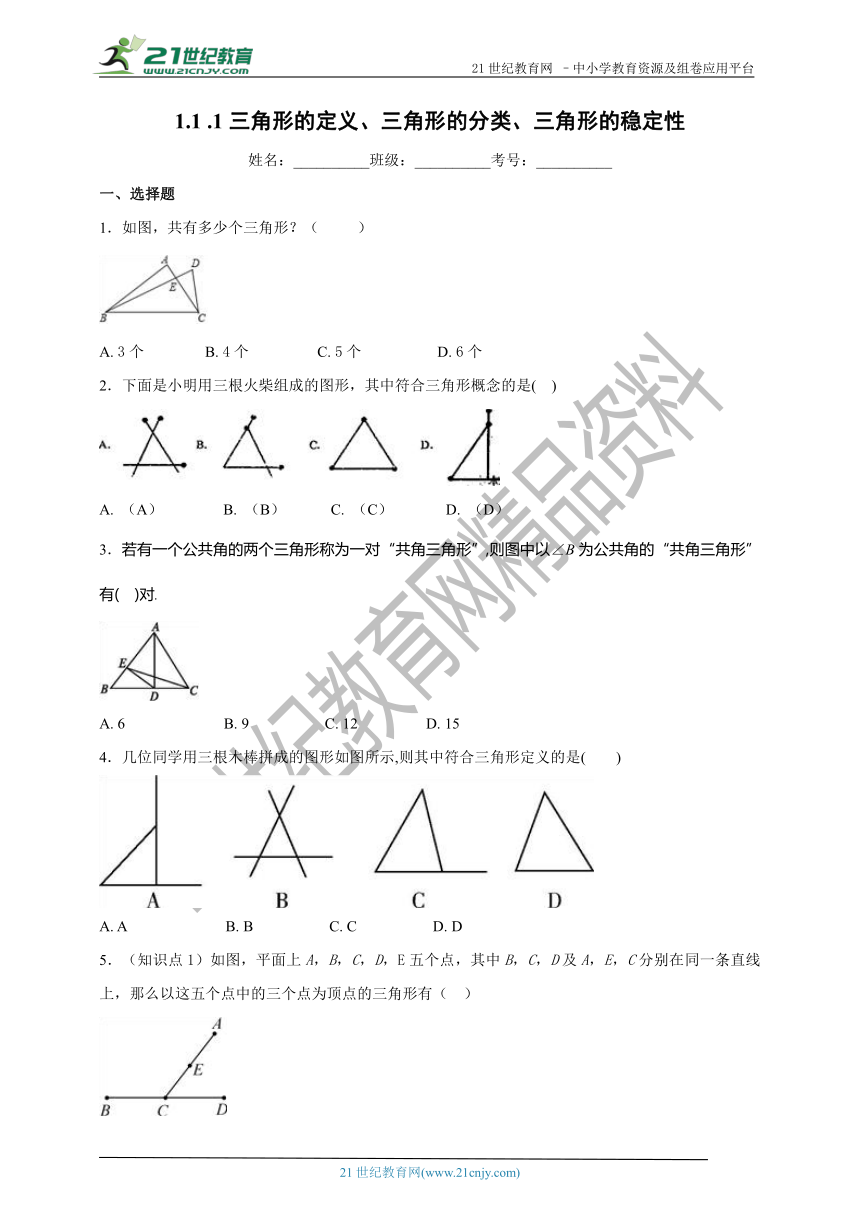 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-18 10:17:27 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.1 .1三角形的定义、三角形的分类、三角形的稳定性
姓名:__________班级:__________考号:__________
一、选择题
1.如图,共有多少个三角形?( )
A. 3个 B. 4个 C. 5个 D. 6个
2.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( )
A. (A) B. (B) C. (C) D. (D)
3.若有一个公共角的两个三角形称为一对“共角三角形”,则图中以∠B为公共角的“共角三角形”有( )对.
A. 6 B. 9 C. 12 D. 15
4.几位同学用三根木棒拼成的图形如图所示,则其中符合三角形定义的是( )
A. A B. B C. C D. D
5.(知识点1)如图,平面上A,B,C,D,E五个点,其中B,C,D及A,E,C分别在同一条直线上,那么以这五个点中的三个点为顶点的三角形有( )
A. 4个 B. 6个 C. 8个 D. 10个
6.三角形纸片内有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,这样的小三角形的个数是( )
A. 299 B. 201 C. 205 D. 207
7.三角形是( )
A. 连接任意三角形组成的图形
B. 由不在同一条直线上的三条线段首尾顺次相接所组成的的图形
C. 由三条线段组成的图形
D. 以上说法均不对
8.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A. 2 B. 4 C. 3 D. 5
9.下列说法正确的是( )
A. 按角分类,三角形可以分为钝角三角形、锐角三角形和等腰直角三角形
B. 按边分类,三角形可分为等腰三角形、不等边三角形和等边三角形
C. 三角形的外角大于任何一个内角
D. 一个三角形中至少有一个内角不大于60°
10.三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
二、填空题
11.(1)如图,点D在△ABC内,写出图中所有除△ABC外的三角形:__________;
(2)在△ACD中,∠ACD所对的边是______;在△ABD中,边AD所对的角是______.
12.如图,在△ABC中, D是BC边上一点,E是AD边上一点.
(1)以AC为边的三角形共有________个,它们是____________________________;
(2)∠1是△________和△________的内角;
(3)在△ACE中,∠CAE的对边是________.
13.工人师傅在做完门框后,为防止变形常常像图中所示的那样上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是_____.
14.如图,自行车的车身为三角形结构,这样做根据的数学道理是____________.
15.如图,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案是________.
三、解答题
16.如图,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
17.如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:
(1)图中有多少个三角形 并把它们表示出来.
(2)△BDF的三个顶点是什么 三条边是什么
(3)以AB为边的三角形有哪些
(4)以F为顶点的三角形有哪些
18.根据下列条件,判断△ABC的形状.
(1)∠A=40°,∠B=80°;
(2)∠A∶∠B∶∠C=2∶3∶7.
19.如图1,在四边形木条框架中,任意添加1根对角线木条,就能使框架的形状稳定.
判断下列说法是否正确.(正确的打“√”,错误的打“×”)
(1)在图2中任意添加2根对角线木条,都能使框架的形状稳定.(____)
(2)在图3中任意添加3根对角线木条,都能使框架的形状稳定.(____)
(3)图4是一个用螺钉将木条链接成的框架,颇具美感,它的形状是稳定的.(____)
参考答案
1.C
【解析】分析:分别找出单个的三角形即可.
详解:三角形有△ABE,△DEC,△BEC,△ABC,△BDC,
故选:C.
点睛:本题考查了三角形的知识,按照一定的顺序找出三角形是解题的关键.
2.C
【解析】∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故选C.
3.A
【解析】试题分析:含有∠B的三角形有:△BDE、△BCE、△ABD、△ABC,则共有6对,故选A.
4.D
【解析】试题分析:因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选D.
点睛:此题考查了三角形的定义.解题的关键是熟练记住定义.
5.C
【解析】不在同一条直线上的三点首尾顺次相接即可得到一个三角形,据此作出判断.能围成的三角形有△BCE,△BCA,△CDE,△CDA,△BDE,△BDA,△AEB,△AED,共8个.故选C.
6.B
【解析】根据题意可以得到当三角形纸片内有个点时,有3个小三角形;当有2个点时,有5个小三角形;当n=3时,有7个小三角形,因而若有n个点时,一定是有2n+1个三角形.
解:根据题意有这样的三角形的个数为:2n=1=2×100+1=201,
故选B.
“点睛”此题主要考查了利用平面内点的个数确定三角形个数,根据n取比较的数值时得到的数值,找出规律,再利用规律解决问题.
7.B
【解析】试题解析:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选B.
8.B
【解析】如图,满足条件的点C共有4个.故选B.
9.D
【解析】分析:根据三角形的分类、三角形的外角和内角的性质得出正确答案.
详解:A、按角分类,三角形可以分为钝角三角形、锐角三角形和直角三角形,故错误;B、按边分类,三角形可分为等腰三角形、不等边三角形,故错误;C、三角形的外角大于任何一个与它不相邻的内角,故错误;D、一个三角形中至少有一个内角不大于60°,故正确,则本题选D.
点睛:本题主要考查的是三角形的分类以及三角形内角和外角的性质,属于基础题型.理解三角形的性质是解决这个问题的关键.
10.C
【解析】∵(a-b)2+|b-c|=0,
∴ ,解得: ,
∴ a=b=c,
又∵a、b、c是△ABC的三边,
∴△ABC是等边三角形.
故选C.
点睛:(1)一个代数式的平方和绝对值都是非负数;(2)两个非负数的和为0,则这两个非负数都为0.
11. △ABD,△ACD,△BCD AD ∠ABD
【解析】解:(1)△ABD,△ACD,△BCD;
(2)AD,∠ABD.
故答案为:(1)△ABD,△ACD,△BCD;(2)AD,∠ABD.
12.(1)3;△ACE,△ACD,△ACB;(2)BCE,CDE;(3)CE.
【解析】由图形可知,以AC为边的三角形有△ACE,△ACD,△ACB, 共3个; ∠1是△CDE和△CBE的内角;在△ACE中,∠CAE的对边是CE.
故答案:(1)3;△ACE,△ACD,△ACB;(2)BCE,CDE;(3)CE.
13.三角形的稳定性.
【解析】这样做的依据是三角形的稳定性,故答案为:三角形的稳定性.
14.三角形具有稳定性
【解析】自行车的车身为三角结构,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
15.③
【解析】根据三角形具有稳定性,四边形不具有稳定性可知最好的加固方案是③.
16.6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形.
17.答案见解析
【解析】试题分析:利用三角形的定义以及三角形有关的角和边概念分别得出即可.
试题解析:
(1)8个:△ABC,△ABF,△ABE,△ABD,△BDF,△AEF,△ACD,△BCE;
(2)三个顶点:B,D,F;三条边:BD,BF,DF;
(3)△ABC,△ABF,△ABD,△ABE;
(4)△ABF,△BDF,△AEF.
点睛:此题主要考查了三角形有关定义,正确把握相关定义是解题关键.
18.(1)△ABC是锐角三角形(2)△ABC是钝角三角形.
【解析】试题分析:(1)根据三角形的内角和是180°求出∠C的度数即可判断△ABC的形状;
(2)因为∠A∶∠B∶∠C=2∶3∶7,所以可设∠A=2x,∠B=3x,∠C=7x,根据三角形内角和是180°列出方程求出∠A、∠B、∠C的度数,即可判断△ABC的度数.
试题解析:
(1)∠C=180°-∠A-∠B=60°,因为40°<60°<80°<90°,所以△ABC是锐角三角形.
(2)设∠A=2x,∠B=3x,∠C=7x,
则2x+3x+7x=180°,解得x=15°.
所以∠C=7×15°=105°.
所以△ABC是钝角三角形.
点睛:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
19. √, ×, √
【解析】试题分析:
根据所添加的对角线木条,结合“三角形具有稳定性,四边形具有不稳定性”分析即可得出结论.
试题解析:
(1)在图2中任意添加2根对角线木条,都能使图形全部由三角形结构组成,所以(1)中说法正确;
(2)如下图,当按图中的方法,在图3中添加3根对角线木条后,图形中有四边形结构,图形结构不稳定,所以(2)说法是错误的;
(3)当用螺钉将木条链接成如图4的框架时,则图中的框架形状全是由三角形结构组成的,所以(3)中的说法是正确的.
即:(1)√;(2)×;(3)√.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.1 .1三角形的定义、三角形的分类、三角形的稳定性
姓名:__________班级:__________考号:__________
一、选择题
1.如图,共有多少个三角形?( )
A. 3个 B. 4个 C. 5个 D. 6个
2.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( )
A. (A) B. (B) C. (C) D. (D)
3.若有一个公共角的两个三角形称为一对“共角三角形”,则图中以∠B为公共角的“共角三角形”有( )对.
A. 6 B. 9 C. 12 D. 15
4.几位同学用三根木棒拼成的图形如图所示,则其中符合三角形定义的是( )
A. A B. B C. C D. D
5.(知识点1)如图,平面上A,B,C,D,E五个点,其中B,C,D及A,E,C分别在同一条直线上,那么以这五个点中的三个点为顶点的三角形有( )
A. 4个 B. 6个 C. 8个 D. 10个
6.三角形纸片内有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,这样的小三角形的个数是( )
A. 299 B. 201 C. 205 D. 207
7.三角形是( )
A. 连接任意三角形组成的图形
B. 由不在同一条直线上的三条线段首尾顺次相接所组成的的图形
C. 由三条线段组成的图形
D. 以上说法均不对
8.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A. 2 B. 4 C. 3 D. 5
9.下列说法正确的是( )
A. 按角分类,三角形可以分为钝角三角形、锐角三角形和等腰直角三角形
B. 按边分类,三角形可分为等腰三角形、不等边三角形和等边三角形
C. 三角形的外角大于任何一个内角
D. 一个三角形中至少有一个内角不大于60°
10.三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
二、填空题
11.(1)如图,点D在△ABC内,写出图中所有除△ABC外的三角形:__________;
(2)在△ACD中,∠ACD所对的边是______;在△ABD中,边AD所对的角是______.
12.如图,在△ABC中, D是BC边上一点,E是AD边上一点.
(1)以AC为边的三角形共有________个,它们是____________________________;
(2)∠1是△________和△________的内角;
(3)在△ACE中,∠CAE的对边是________.
13.工人师傅在做完门框后,为防止变形常常像图中所示的那样上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是_____.
14.如图,自行车的车身为三角形结构,这样做根据的数学道理是____________.
15.如图,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案是________.
三、解答题
16.如图,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
17.如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:
(1)图中有多少个三角形 并把它们表示出来.
(2)△BDF的三个顶点是什么 三条边是什么
(3)以AB为边的三角形有哪些
(4)以F为顶点的三角形有哪些
18.根据下列条件,判断△ABC的形状.
(1)∠A=40°,∠B=80°;
(2)∠A∶∠B∶∠C=2∶3∶7.
19.如图1,在四边形木条框架中,任意添加1根对角线木条,就能使框架的形状稳定.
判断下列说法是否正确.(正确的打“√”,错误的打“×”)
(1)在图2中任意添加2根对角线木条,都能使框架的形状稳定.(____)
(2)在图3中任意添加3根对角线木条,都能使框架的形状稳定.(____)
(3)图4是一个用螺钉将木条链接成的框架,颇具美感,它的形状是稳定的.(____)
参考答案
1.C
【解析】分析:分别找出单个的三角形即可.
详解:三角形有△ABE,△DEC,△BEC,△ABC,△BDC,
故选:C.
点睛:本题考查了三角形的知识,按照一定的顺序找出三角形是解题的关键.
2.C
【解析】∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故选C.
3.A
【解析】试题分析:含有∠B的三角形有:△BDE、△BCE、△ABD、△ABC,则共有6对,故选A.
4.D
【解析】试题分析:因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选D.
点睛:此题考查了三角形的定义.解题的关键是熟练记住定义.
5.C
【解析】不在同一条直线上的三点首尾顺次相接即可得到一个三角形,据此作出判断.能围成的三角形有△BCE,△BCA,△CDE,△CDA,△BDE,△BDA,△AEB,△AED,共8个.故选C.
6.B
【解析】根据题意可以得到当三角形纸片内有个点时,有3个小三角形;当有2个点时,有5个小三角形;当n=3时,有7个小三角形,因而若有n个点时,一定是有2n+1个三角形.
解:根据题意有这样的三角形的个数为:2n=1=2×100+1=201,
故选B.
“点睛”此题主要考查了利用平面内点的个数确定三角形个数,根据n取比较的数值时得到的数值,找出规律,再利用规律解决问题.
7.B
【解析】试题解析:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选B.
8.B
【解析】如图,满足条件的点C共有4个.故选B.
9.D
【解析】分析:根据三角形的分类、三角形的外角和内角的性质得出正确答案.
详解:A、按角分类,三角形可以分为钝角三角形、锐角三角形和直角三角形,故错误;B、按边分类,三角形可分为等腰三角形、不等边三角形,故错误;C、三角形的外角大于任何一个与它不相邻的内角,故错误;D、一个三角形中至少有一个内角不大于60°,故正确,则本题选D.
点睛:本题主要考查的是三角形的分类以及三角形内角和外角的性质,属于基础题型.理解三角形的性质是解决这个问题的关键.
10.C
【解析】∵(a-b)2+|b-c|=0,
∴ ,解得: ,
∴ a=b=c,
又∵a、b、c是△ABC的三边,
∴△ABC是等边三角形.
故选C.
点睛:(1)一个代数式的平方和绝对值都是非负数;(2)两个非负数的和为0,则这两个非负数都为0.
11. △ABD,△ACD,△BCD AD ∠ABD
【解析】解:(1)△ABD,△ACD,△BCD;
(2)AD,∠ABD.
故答案为:(1)△ABD,△ACD,△BCD;(2)AD,∠ABD.
12.(1)3;△ACE,△ACD,△ACB;(2)BCE,CDE;(3)CE.
【解析】由图形可知,以AC为边的三角形有△ACE,△ACD,△ACB, 共3个; ∠1是△CDE和△CBE的内角;在△ACE中,∠CAE的对边是CE.
故答案:(1)3;△ACE,△ACD,△ACB;(2)BCE,CDE;(3)CE.
13.三角形的稳定性.
【解析】这样做的依据是三角形的稳定性,故答案为:三角形的稳定性.
14.三角形具有稳定性
【解析】自行车的车身为三角结构,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
15.③
【解析】根据三角形具有稳定性,四边形不具有稳定性可知最好的加固方案是③.
16.6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形.
17.答案见解析
【解析】试题分析:利用三角形的定义以及三角形有关的角和边概念分别得出即可.
试题解析:
(1)8个:△ABC,△ABF,△ABE,△ABD,△BDF,△AEF,△ACD,△BCE;
(2)三个顶点:B,D,F;三条边:BD,BF,DF;
(3)△ABC,△ABF,△ABD,△ABE;
(4)△ABF,△BDF,△AEF.
点睛:此题主要考查了三角形有关定义,正确把握相关定义是解题关键.
18.(1)△ABC是锐角三角形(2)△ABC是钝角三角形.
【解析】试题分析:(1)根据三角形的内角和是180°求出∠C的度数即可判断△ABC的形状;
(2)因为∠A∶∠B∶∠C=2∶3∶7,所以可设∠A=2x,∠B=3x,∠C=7x,根据三角形内角和是180°列出方程求出∠A、∠B、∠C的度数,即可判断△ABC的度数.
试题解析:
(1)∠C=180°-∠A-∠B=60°,因为40°<60°<80°<90°,所以△ABC是锐角三角形.
(2)设∠A=2x,∠B=3x,∠C=7x,
则2x+3x+7x=180°,解得x=15°.
所以∠C=7×15°=105°.
所以△ABC是钝角三角形.
点睛:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
19. √, ×, √
【解析】试题分析:
根据所添加的对角线木条,结合“三角形具有稳定性,四边形具有不稳定性”分析即可得出结论.
试题解析:
(1)在图2中任意添加2根对角线木条,都能使图形全部由三角形结构组成,所以(1)中说法正确;
(2)如下图,当按图中的方法,在图3中添加3根对角线木条后,图形中有四边形结构,图形结构不稳定,所以(2)说法是错误的;
(3)当用螺钉将木条链接成如图4的框架时,则图中的框架形状全是由三角形结构组成的,所以(3)中的说法是正确的.
即:(1)√;(2)×;(3)√.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
