1.3 证明、三角形的外角性质同步作业

21世纪教育网 –中小学教育资源及组卷应用平台
1.3 证明、三角形的外角性质同步作业
姓名：__________班级：__________考号：__________
一、选择题
1．三角形中∠B的平分线和外角的平分线的夹角是（ ）．
A. 60° B. 90° C. 45° D. 135°
2．一把直尺和一块三角板ABC（其中∠B=30°，∠C=90°）摆放位置如图所示，直尺一边与三角板的两直角边分别交于点D，点E，另一边与三角板的两直角边分别交于点F，点A，且∠CDE=50°，那么∠BAF的大小为（　　）
A. 20° B. 40° C. 45° D. 50°
3．某校九年级四个班的代表队准备举行篮球友谊赛．甲、乙、丙三位同学预测比赛的 结果如下：
甲说：“902班得冠军，904班得第三”；
乙说：“901班得第四，903班得亚军”；
丙说：“903班得第三，904班得冠军”．
赛后得知，三人都只猜对了一半，则得冠军的是
A．901班 B．902班 C．903班 D．904班
4．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（　　）
A. 40° B. 45° C. 50° D. 55°
5．已知直线a∥b，将一块含45°角的直角三角板（∠C=90°）按如图所示的位置摆放，若∠1=55°，则∠2的度数为（　　）
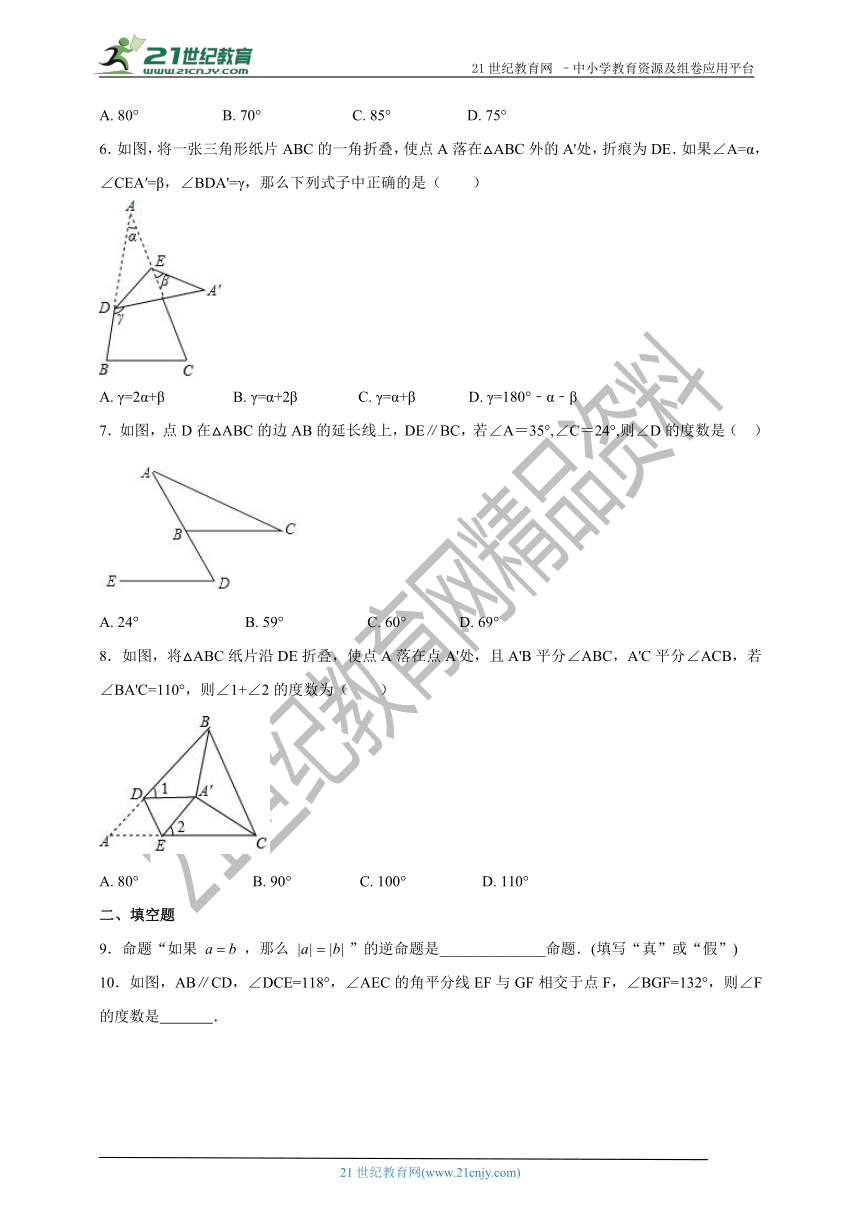
A. 80° B. 70° C. 85° D. 75°
6．如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，那么下列式子中正确的是（　　）
A. γ=2α+β B. γ=α+2β C. γ=α+β D. γ=180°﹣α﹣β
7．如图，点D在△ABC的边AB的延长线上，DE∥BC，若∠A＝35°,∠C＝24°,则∠D的度数是（ ）
A. 24° B. 59° C. 60° D. 69°
8．如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C=110°，则∠1+∠2的度数为（　　）
A. 80° B. 90° C. 100° D. 110°
二、填空题
9．命题“如果 a b ，那么 |a| |b| ”的逆命题是______________命题．(填写“真”或“假”)
10．如图，AB∥CD，∠DCE=118°，∠AEC的角平分线EF与GF相交于点F，∠BGF=132°，则∠F的度数是　 　．
11．甲、乙、丙三人进行乒乓球比赛，规则是：两人比赛，另一人当裁判，输者将在下一局中担任裁判，每一局比赛没有平局．已知甲、乙各比赛了4局，丙当了3次裁判．则第二局的输者是________。
12．如图，CE 是△ABC 的外角∠ACD 的平分线，交 BA 的延长线于点 E，若∠E=20°，∠B=30°，则∠BAC=_____．
13．如图，在四边形ABCD中，∠A与∠DCB互补，E为BC 延长线上的点，且∠1+∠2+∠DCE，则∠A的度数是____________．
14．如图，BC∥DE，已知∠B＝22 ，∠D＝51 ，则∠A＝________。
15．如图，在△ABC中，EF∥BC，∠ACG是△ABC的外角，∠BAC的平分线交BC于点D，记∠ADC=α，∠ACG=β，∠AEF=γ，则：α、β、γ三者间的数量关系式是______.
三、解答题
16．已知：如图，∠2是△ABC的一个外角．
求证：∠2=∠A+∠B．
证明：如图，
∵∠A+∠B+∠1=180° （ ）
∠1+∠2=180° （ ）
∴∠2=∠A+∠B （ ）
17．如图，AD⊥BD,AE平分∠BAD, ∠B=30°，∠ACD=70°，求∠EAB和∠CAE的度数.
18．如图，∠MAN=100°，点B、C是射线AM、AN上的动点，∠ACB的平分线和∠MBC的平分线所在直线相交于点D，求∠BDC的大小
19．证明：两条平行直线被第三条直线所截，一对同旁内角的平分线互相垂直.
已知:
求证： .
证明：
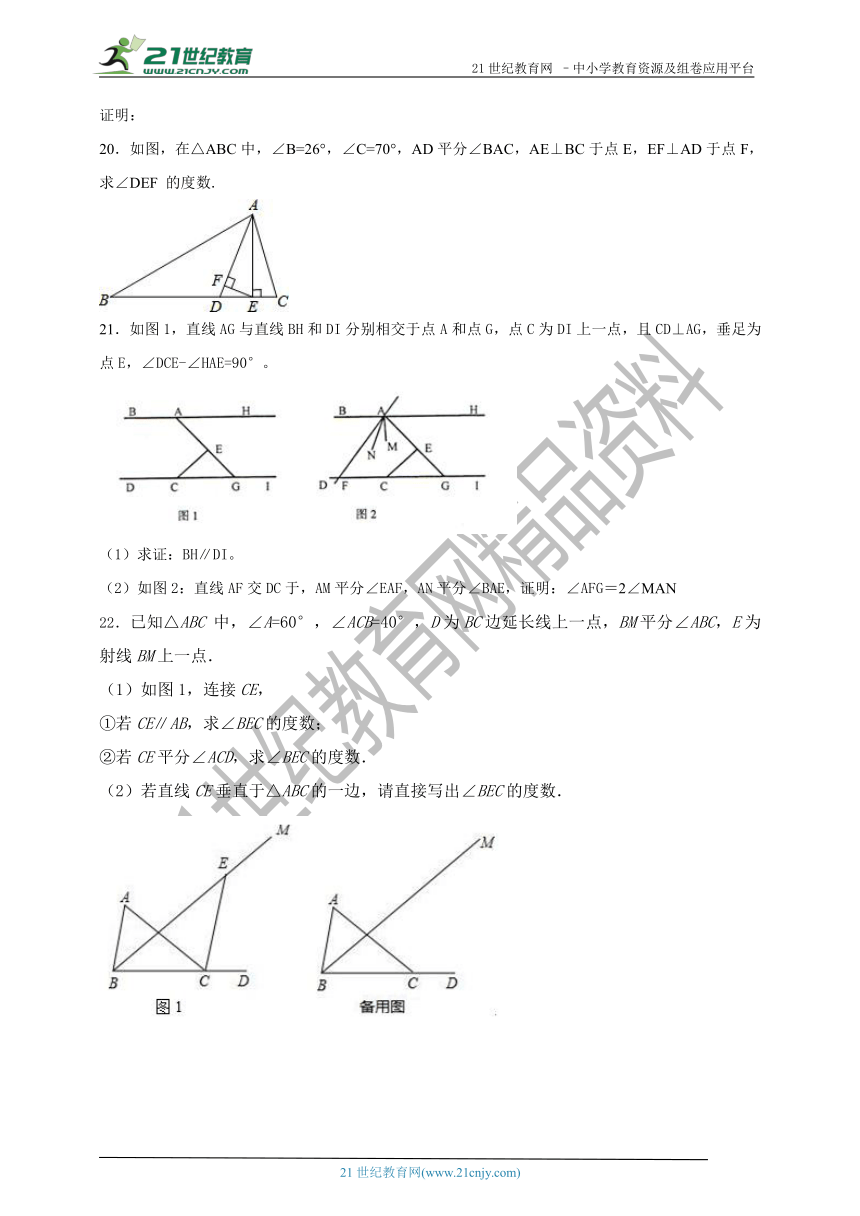
20．如图，在△ABC中，∠B=26°，∠C=70°，AD平分∠BAC，AE⊥BC于点E，EF⊥AD于点F，求∠DEF 的度数.
21．如图1，直线AG与直线BH和DI分别相交于点A和点G，点C为DI上一点，且CD⊥AG，垂足为点E，∠DCE-∠HAE=90°。
（1）求证：BH∥DI。
（2）如图2：直线AF交DC于，AM平分∠EAF，AN平分∠BAE，证明：∠AFG＝2∠MAN
22．已知△ABC 中，∠A=60°，∠ACB=40°，D为BC边延长线上一点，BM平分∠ABC，E为射线BM上一点．
（1）如图1，连接CE，
①若CE∥AB，求∠BEC的度数；
②若CE平分∠ACD，求∠BEC的度数．
（2）若直线CE垂直于△ABC的一边，请直接写出∠BEC的度数．
参考答案
1．B
【解析】
如图，BD平分∠ABF，BE平分∠ABC，
∴∠ABD=∠ABF，∠ABE=∠ABC，
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=（∠ABF+∠ABC）=90°.
故选B.
2．A
【解析】分析：根据平行线的性质得出∠AFC的度数，然后根据三角形外角的性质得出答案．
详解：∵DE∥AF， ∴∠AFC=∠CDE=50°，
根据三角形外角的性质可得：∠AFC=∠B+∠BAF，∴∠BAF=50°－30°=20°，故选A．
点睛：本题主要考查的是平行线的性质以及三角形外角的性质，属于基础题型．明白平行线的性质是解题的关键．
3．B
【解析】
试题解析：假设甲说的“902班得冠军”是正确的，那么丙说的“904班得冠军”是错误的，
“903班得第三”就是正确的，那么乙说的“903班得亚军”是错误的，
“901班得第四”是正确的，这样三人都猜对了一半，且没矛盾．
故丙猜测是正确的．
故选B.
考点：命题.
4．C
【解析】【分析】根据三角形外角性质求出∠ACD，根据角平分线定义求出即可．
【详解】∵∠A=60°，∠B=40°，
∴∠ACD=∠A+∠B=100°，
∵CE平分∠ACD，
∴∠ECD=∠ACD=50°，
故选C．
【点睛】本题考查了角平分线定义和三角形外角性质，熟记三角形外角性质的内容是解此题的关键．
5．A
【解析】【分析】如图，先根据三角形外角的性质求出∠4的度数，再根据平行线的性质求出∠5的度数，最后根据邻补角的定义进行求解即可得.
【详解】如图，
∵∠1=∠3=55°，∠B=45°，
∴∠4=∠3+∠B=100°，
∵a∥b，
∴∠5=∠4=100°，
∴∠2=180°﹣∠5=80°，
故选A．
【点睛】本题考查了平行线的性质，三角形内角和定理，三角形的外角的性质等知识，结合图形灵活运用相关的知识解决问题是关键.
6．A
【解析】分析：根据三角形的外角得：∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，代入已知可得结论．
详解：由折叠得：∠A=∠A'，如图，
∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，
∵∠A=α，∠CEA′=β，∠BDA'=γ，
∴∠BDA'=γ=α+α+β=2α+β，
故选：A．
点睛：本题考查了三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键．
7．B
【解析】【分析】根据三角形外角性质得∠DBC=∠A+∠C，再由平行线性质得∠D=∠DBC.
【详解】∵∠A=35°，∠C=24°，
∴∠DBC=∠A+∠C=35°+24°=59°，
又∵DE∥BC，
∴∠D=∠DBC=59°，
故选B.
【点睛】本题考查了平行线的性质，三角形外角的性质，熟练掌握相关的性质是解题的关键.
8．A
【解析】分析：连接AA′．首先求出∠BAC，再证明∠1+∠2=2∠BAC即可解决问题．
详解：连接AA′．
∵A'B平分∠ABC，A'C平分∠ACB，∠BA'C=110°，∴∠A′BC+∠A′CB=70°，∴∠ABC+∠ACB=140°，∴∠BAC=180°﹣140°=40°．
∵∠1=∠DAA′+∠DA′A，∠2=∠EAA′+∠EA′A．
∵∠DAA′=∠DA′A，∠EAA′=∠EA′A，∴∠1+∠2=2（∠DAA′+∠EAA′）=2∠BAC=80°．
故选A．
点睛：本题考查了三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识，属于中考常考题型．
9．假
【解析】“如果ab，那么|a| |b|”逆命题是：如果|a||b|，那么ab，该命题为假命题.
故答案为假.
10．11°．
【解析】分析：本题考查的是平行线的内错角相等，角平分线的性质和三角形外角的性质.
解析：∵AB//CD，∠DCE=118°，∴∠AEC=118°, ∵∠AEC的角平分线EF与GF相交线于点F, ∴∠AEF=∠FEC=59°, ∵∠BGF=132°, ∴∠F=11°.
故答案为11°.
11．丙
【解析】由题意，知：由丙当了3次裁判知有三场比赛是甲乙比赛，丙当裁判，且这三场比赛分别是第一局，第三局，第五局：
第一局：甲VS乙，丙当裁判；
第三局：甲VS乙，丙当裁判；
第五局：甲VS乙，丙当裁判；
由于输球的人下局当裁判，因此第二场输的人是丙。
故答案是：丙。
12．70°
【解析】分析：根据三角形外角性质求出∠ECD，即可求出∠ACE，根据三角形外角性质求出∠BAC即可．
详解：∵∠B=30°,∠E=20°，
∴∠ECD=∠B+∠E=50°，
∵CE平分∠ACD，
∴∠ACE=∠ECD=50°，
∴∠BAC=∠ACE+∠E=50°+20°=70°.
故答案为：70°.
点睛：本题考查了三角形的外角性质，角平分线定义的应用，注意：三角形的一个外角等于和它不相邻的两个内角的和.
13．112°
【解析】分析：根据三角形外角的性质得到∠DCE的度数，再根据同角的补角相等得到∠A=∠DCE，即可得到结论．
详解：∵∠1+∠2+∠DCE=224°，∠1+∠2=∠DCE，∴∠DCE=112°．
∵∠A+∠DCB=180°，∠DCE+∠DCB=180°，∴∠A=∠DCE=112°．
故答案为：112°．
点睛：本题考查了三角形外角的性质和同角的补角相等．熟练掌握三角形外角的性质和同角的补角相等是解题的关键．
14．29
【解析】分析：设AD与BC相交于点F．由平行线的性质得到∠AFC=∠ADE=51°．再由三角形外角的性质即可得到结论．
详解：设AD与BC相交于点F．
∵BC∥DE，∴∠AFC=∠ADE=51°．
∵∠A+∠B=∠AFC，∴∠A=∠AFC－∠B=51°－22°=29°．
故答案为：29°．
点睛：本题考查了平行线的性质和三角形外角的性质．熟练掌握平行线的性质和三角形外角的性质是解题的关键．
15．2∠α=∠β+∠γ.
【解析】分析：根据两直线平行，同位角相等可得∠B=γ，再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BAD、∠CAD，再根据角平分线的定义可得∠BAD=∠CAD，然后列出方程整理即可得解．
详解：∵EF∥BC，
∴∠B=γ，
由三角形的外角性质得，∠BAD=α-∠B=α-γ，
∠CAD=β-α，
∵AD是∠BAC的平分线，
∴∠BAD=∠CAD，
∴α-γ=β-α，
∴β+γ=2α．
故答案为：β+γ=2α．
点睛：本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记性质是解题的关键．
16．三角形内角和定理；邻补角的定义；等量代换
【解析】试题分析：根据三角形内角和定理和平角的定义得出∠A+∠B+∠1=180°，∠1+∠2=180°，从而得出∠A+∠B+∠1=∠1+∠2，即∠2=∠A+∠B．
试题解析：证明：∵∠A+∠B+∠1=180°(三角形内角和定理)，
∠1+∠2=180°(邻补角的定义)，
∴∠2=∠A+∠B(等量代换)．
故答案为：三角形内角和定理，邻补角的定义，等量代换.
17．∠EAB=30°．∠CAE=10°.
【解析】分析：根据直角三角形的两个锐角互余，得∠BAD=60°，根据角平分线定义求得∠EAB；根据三角形的外角的性质，求得∠BAC，从而求得∠CAE．
详解：∵AD⊥BD，∠B=30°，
∴∠BAD=60°．
又AE平分∠BAD，
∴∠EAB=30°．
∵∠ACD=70°，
∴∠BAC=∠ACD-∠B=40°．
∴∠CAE=∠BAC-∠EAB=10°．
点睛：此题综合运用了三角形的内角和定理、三角形的外角性质以及角平分线定义．
三角形的内角和是180°；三角形的外角等于和它不相邻的两个内角的和．
18．∠BDC＝50°
【解析】试题分析：根据角平分线定义得出∠ACB=2∠DCB，∠MBC=2∠CBE，根据三角形外角性质得出2∠D+∠ACB=∠A+∠ACB，求出∠A=2∠D，即可求出答案．
解：由∠CBE是三角形CDB的外角，所以∠BDC＝∠CBM－∠ACB=100°，
又因为∠ACB的平分线和∠MBC的平分线
所以∠BDC＝
19．见解析.
【解析】试题分析：根据题意画出图形，写出已知与求证，证明过程为：由AB与CD平行，利用两直线平行同旁内角互补得到∠BEF+∠EFD=180°，再由EG与FG为角平分线，利用角平分线定义及等量代换得到∠GEF+∠EFG=90°，根据三角形的内角和定理即可得∠EGF=90°，结论得证．
试题解析：
已知：直线AB∥CD，直接EF分别交AB，CD于点E，F，∠BEF，∠EFD的平分线交于G点.
求证：EG⊥FG
证明：∵AB∥CD，
∴∠BEF+∠EFD=180°，
∵EG平分∠BEF,FG平分∠EFD，
∴∠GEF=∠BEF，∠EFG=∠EFD，
∴∠GEF+∠EFG=∠BEF+∠EFD=×180°=90°，
∴∠EGF=180°-(∠GEF+∠EFG)=90°，
∴EG⊥FG
20．22°.
【解析】试题分析：根据三角形的内角和求出的度数,根据角平分线的性质求出依据三角形外角的性质求出的度数，直角三角形的两锐角互余，即可求出的度数.
试题解析：
中，
平分，
是的外角,
,
于，
21．证明见解析
【解析】分析：（1）根据三角形外角的性质可得∠DCE=∠EGC+90°，再结合∠DCE－∠HAE=90°可得∠CGA=∠HAE，即可证得结论；
（2）根据角平分线的定义表示出∠EAM、∠EAN，然后求出∠MAN，再根据两直线平行，内错角相等可得∠BAF=∠AFG，从而得解.
详解：（1）∵∠DCE＋∠ECG=180°，
∠CEG＋∠CGA＋∠ECG=180°，
所以∠DCE=∠CEG＋∠CGA.
因为CD⊥AG，
所以∠DCE－∠CGA=∠CEG=90°.
又因为∠DCE－∠HAE=90°，
所以∠CGA=∠HAE，
所以BH∥DI；
（2）因为AM平分∠EAF， AN平分∠BAE，
所以∠EAM=∠FAM ， ∠EAN=∠BAN.
又因为∠MAN=∠EAN－∠EAM，
所以∠MAN=∠BAN－∠FAM.
又因为∠BAN=∠BAF＋∠FAN，
∠FAM=∠MAN＋∠FAN，
所以∠MAN=∠BAF－∠MAN，
所以∠BAF=2∠MAN.
又因为BH∥DI，
所以∠AFG=∠BAF，
所以∠AFG=2∠MAN.
点睛：本题考查了平行线的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记平行线的判定与性质是解题的关键.
22．（1）①40°；②30°；(2)50°，130°，10°
【解析】试题分析：（1）①根据三角形的内角和得到∠ABC=80°，由角平分线的定义得到∠ABE=∠ABC=40°，根据平行线的性质即可得到结论；
②根据邻补角的定义得到∠ACD=180°-∠ACB=140°，根据角平分线的定义得到∠CBE=∠ABC=40°，∠ECD=∠ACD=70°，根据三角形的外角的性质即可得到结论；
（2）①如图1，当CE⊥BC时，②如图2，当CE⊥AB于F时，③如图3，当CE⊥AC时，根据垂直的定义和三角形的内角和即可得到结论．
试题解析：（1）①∵∠A=60°，∠ACB=40°，
∴∠ABC=80°，
∵BM平分∠ABC，
∴∠ABE=∠ABC=40°，
∵CE∥AB，
∴∠BEC=∠ABE=40°；
②∵∠A=60°，∠ACB=40°，
∴∠ABC=80°，∠ACD=180°-∠ACB=140°，
∵BM平分∠ABC，CE平分∠ACD，
∴∠CBE=∠ABC=40°，∠ECD=∠ACD=70°，
∴∠BEC=∠ECD-∠CBE=30°；
（2）①如图1，当CE⊥BC时，
∵∠CBE=40°，
∴∠BEC=50°；
②如图2，当CE⊥AB于F时，
∵∠ABE=40°，
∴∠BEC=90°+40°=130°，
③如图3，当CE⊥AC时，
∵∠CBE=40°，∠ACB=40°，
∴∠BEC=180°-40°-40°-90°=10°．
【点睛】本题考查了平行线的性质，角平分线的定义，垂直的定义，三角形的内角和，三角形的外角的性质，正确的画出图形是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)