1.4 全等三角形同步作业

21世纪教育网 –中小学教育资源及组卷应用平台
1.4 全等三角形同步作业
姓名：__________班级：__________考号：__________
一、选择题
1．下列图形是全等图形的是（ ）
A. B.
C. D.
2．如图所示，图中的两个三角形能完全重合，下列写法正确的是( )
A. △ABE≌△AFB B. △ABE≌△ABF C. △ABE≌△FBA D. △ABE≌△FAB
3．如图，△ABE≌△ACD，∠B=50°，∠AEC=120°，则∠DAC的度数是（　　）
A. 120° B. 70° C. 60° D. 50°
4．如图，△ABC≌△AED，点D在BC上，若， 则 的度数是（ ）
A. B. C. D.
5．如图是两个全等三角形，则∠1的度数为(　　)
A. 62° B. 72° C. 76° D. 66°
6．如图，△ABC≌△BAD，如果AB=6cm，BD=5cm，AD=4cm，那么BC的长是( )
A. 4cm B. 5cm C. 6cm D. 无法确定
7．如图，△ABC ≌△DEF，则此图中相等的线段有（ ）
A. 2对 B. 3对 C. 4对 D. 5对
8．下列说法正确的个数为 (　　)
(1)形状相同的两个三角形是全等三角形;(2)在两个三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应角平分线分别相等.
A. 3 B. 2 C. 1 D. 0
二、填空题
9．如图，四边形ABCD与四边形A′B′C′D′全等，则∠A′=________ ，∠A=________ ，B′C′=________ ，AD=________ ．
10．如图⑴～⑿中全等的图形是_____和______；_____和______；_____和______；
_____和______；_____和______；_____和______；（填图形的序号）
11．如图，△ABE≌△ACD，AB＝10cm，∠A＝60°，∠B＝30°，则∠ADC＝________°，AD＝________cm.
12．如图，△ABD≌△ABC，∠C=100，∠ABD=30，那么∠DAB=_____.
13．如图，已知△ABD≌△ACE，且AB=8，BD=7，AD=6，则BC=______．
14．14．如图，B、C、D在同一直线上，△BAE≌△BCE，△BAE≌△DCE，则∠D＝______.
15．如图，△ABC≌△DCB，若AC=10，DE=3，则CE的长为________ .
三、解答题
16．已知：如图，△ABD与△CDB全等，∠ABD＝∠CDB，写出其余的对应角和各对对应边．
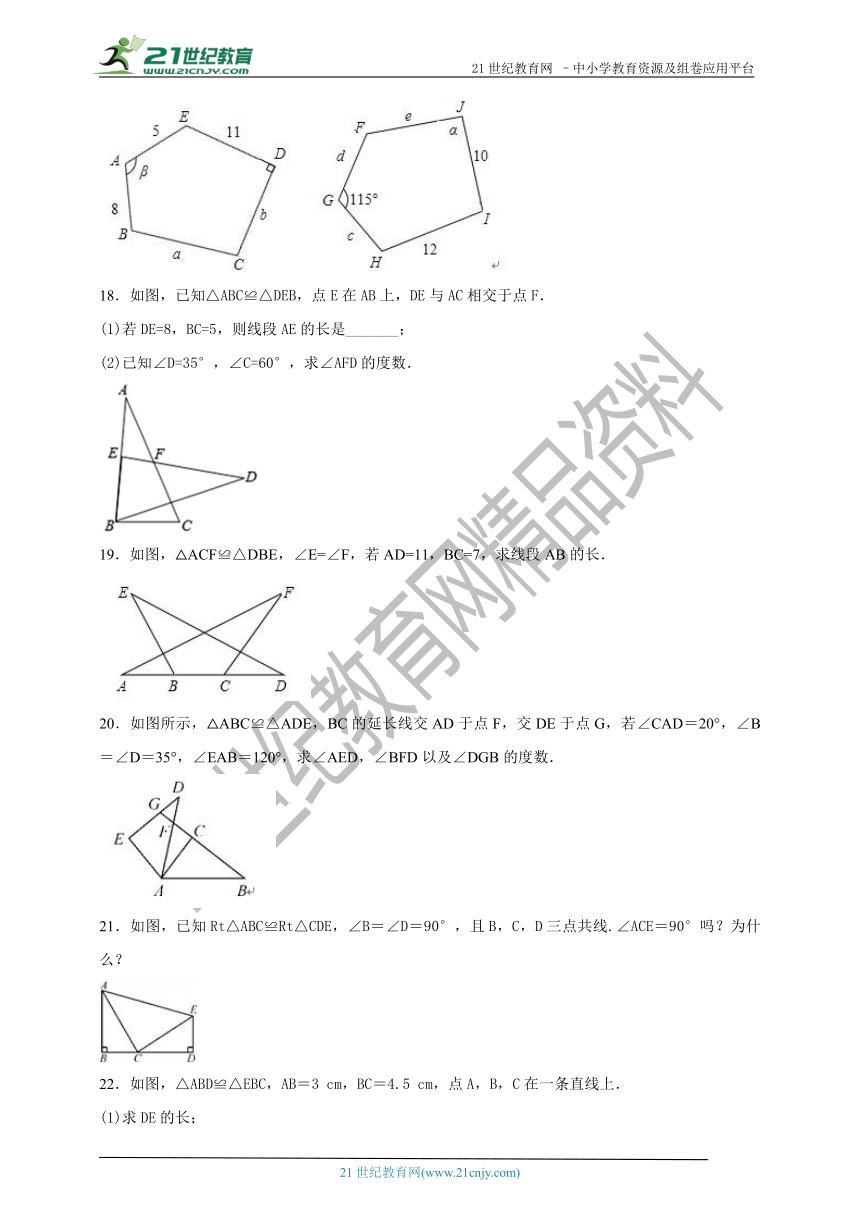
17．图中所示的是两个全等的五边形，∠β=115°，d=5，指出它们的对应顶点 对应边与对应角，并说出图中标的a，b，c，e，α各字母所表示的值．

18．如图，已知△ABC≌△DEB，点E在AB上，DE与AC相交于点F．
(1)若DE=8，BC=5，则线段AE的长是_______；
(2)已知∠D=35°，∠C=60°，求∠AFD的度数．
19．如图，△ACF≌△DBE，∠E=∠F，若AD=11，BC=7，求线段AB的长．
20．如图所示，△ABC≌△ADE，BC的延长线交AD于点F，交DE于点G，若∠CAD＝20°，∠B＝∠D＝35°，∠EAB＝120°，求∠AED，∠BFD以及∠DGB的度数．
21．如图，已知Rt△ABC≌Rt△CDE，∠B＝∠D＝90°，且B，C，D三点共线.∠ACE＝90°吗？为什么？
22．如图，△ABD≌△EBC，AB＝3 cm，BC＝4.5 cm，点A，B，C在一条直线上．
(1)求DE的长；
(2)判断AC与BD的位置关系，并说明理由．
参考答案
1．B
【解析】试题解析：A、两个图形相似，错误；
B、两个图形全等，正确；
C、两个图形相似，错误；
D、两个图形不全等，错误；
故选B.
2．B
【解析】解：要把对应顶点写在对应位置．∵B和B对应，A和A对应，E和F对应，故△ABE≌△ABF．故选B．
3．B
【解析】分析：由全等三角形性质可得∠ADC=∠AEB=60°，∠C=∠B=50°，再根据三角形内角和定理可得∠DAC=180°-50°-60°.
详解：∵∠AEC=120°，
∴∠AEB=180°-120°=60°，
∵△ABE≌△ACD，
∴∠ADC=∠AEB=60°，∠C=∠B=50°，
∴∠DAC=180°-50°-60°=70°，
故选：B.
点睛：本题考核知识点：全等三角形性质. 解题关键点：熟练运用全等三角形性质.
4．C
【解析】分析：根据全等三角形的性质：对应角相等解答即可．
详解：∵△ABC≌△ADE，∴∠B=∠E．
∵∠EGA=∠DGB，∴∠BDE=∠EAB=52°，
∴∠CDE=180°－∠BDE=180°－52°=128°．
故选C．
点睛：本题考查了全等三角形的性质，三角形内角和定理、邻补角的定义的应用，熟练掌握全等三角形的性质是解题的关键．
5．C
【解析】分析：根据三角形内角和定理计算出∠2的度数，然后再根据全等三角形的对应角相等可得∠1=∠2．
详解：根据三角形内角和可得
因为两个三角形全等，
所以
故选C.
点睛：考查三角形全等的性质，掌握全等三角形的对应边相等，对应角相等是解题的关键.
6．A
【解析】【分析】根据全等三角形的对应边相等可得出BC=AD，据此即可得.
【详解】∵△ABC≌△BAD，AD=4cm，
∴BC=AD=4cm，
故选A．
【点睛】本题考查了全等三角形的性质，熟记全等三角形的对应边相等，对应角相等是解决此类问题的关键.
7．C
【解析】分析：1.△ABC≌△DEF，则三组对应边分别相等.
2.边BC与EF有公共边EC，所以BE与CF相等.
详解：∵△ABC≌△DEF，
∴AB=DE,AC=DF,BC=EF,
又∵BC与EF有公共边EC，
∴BE=CF.
故选：C.
点睛：本题考查了全等三角形对应边相等.
8．C
【解析】(1)形状相同、大小相等的两个三角形是全等形,而原说法没有指出大小相等这一点,故(1)错误；(2)在两个全等三角形中,对应角相等,对应边相等,而非相等的角是对应角,相等的边是对应边,故(2)错误；(3)全等三角形对应边上的高、中线及对应角平分线分别相等,故(3)正确。
故选：C.
点睛：根据全等三角形的概念：能够完全重合的图形是全等图形，及全等图形性质：全等图形的对应边、对应角分别相等，但相等的角和相等的边不一定是对应角和对应边；全等三角形对应边上的高、中线及对应角平分线分别相等.
9．120°；70°；12；6
【解析】∵四边形ABCD与四边形A′B′C′D′全等，
由题意得：∠A′=∠D =∠120°，∠D′=∠A=70°，B′C′=CB=12，AD = D′A′=6．
10． （1）、（4）；（2）、（12）；（3）、（11）；（5）、（9）；（6）、（8）；（7）、（10）
【解析】通过观察可以发现：（1）和（4）、（2）和（12）、（3）和（11）、（5）和（9）、（6）和（8）、（7）和（10）是全等形，
故答案为：（1）、（4）；（2）、（12）；（3）、（11）；（5）、（9）；（6）、（8）；（7）、（10）.
11． 90 5
【解析】【分析】根据∠A=60°，∠B=30°可得∠AEB=90°，根据AB=10cm以及直角三角形的性质可得AE=5cm，根据三角形全等可得：AD=AE=5cm，∠ADC=∠AEB=90°.
【详解】在三角形ABE中，∠A=60°，∠B=30°
所以，∠AEB=180-∠A-∠B= 90°,
因为，AB=10cm
所以，AE==5cm，
因为，△ABE≌△ACD，
所以，AD=AE=5cm，∠ADC=∠AEB=90°.
故答案为：(1). 90 (2). 5
【点睛】本题考核知识点：全等三角形的性质. 解题关键点：熟记全等三角形的性质，证角相等和边相等.
12．50
【解析】【分析】要求∠DAB的度数，只要求出∠DAB+∠D，利用全等三角形的对应角相等，求出∠D的大小利用三角形内角和定理即可求得答案．
【详解】∵△ABC≌△ABD，∠C=100°，∠ABD=30°，
∴∠D=∠C=100°，
又∵∠ABD=30°，
∴∠DAB=180°-∠D-∠ABD=180°-100°-30°=50°，
故答案为：50.
【点睛】本题考查了全等三角形的性质，三角形内角和定理，熟练掌握全等三角形的性质及三角形的内角和定理是解决本题的关键.
13．2．
【解析】∵△ABD≌△ACE，∴AD=AC=6，∵AB=8，∴BC=8﹣6=2，故答案为2．
14．30°
【解析】试题解析：∵△BAE≌△BCE，△BAE≌△DCE，
∴∠A=∠ECB=∠ECD，∠ABE=∠CBE=∠D，
又∵B、C、D在同一直线上，
∴∠ECB+∠ECD=180°，
∴∠A=∠ECB=∠ECD=90°，
∴∠ABE+∠CBE+∠D=90°，
∴3∠D=90°，
∴∠D=30°．
故答案为：30°．
15．7
【解析】分析：根据全等三角形的对应边相等解答．
详解：∵△ABC≌△DCB，
∴AB=DC，∠A=∠D，
在△ABE和△DCE中，
，
∴△ABE≌△DCE，
∴AE=DE=3，
∴CE=AC-AE=7，
故答案为7．
点睛：本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．
16．∠A与∠C，∠ADB与∠CBD是对应角；BD与DB，AD与CB，AB与CD是对应边．
【解析】试题分析：关键是找准对应顶点．
试题解析：解：△ABD与△CDB全等，∠ABD＝∠CDB，则∠A与∠C，∠ADB与∠CBD是对应角；BD与DB，AD与CB，AB与CD是对应边．
17．a=12，c=8，b=10，e=11，α=90°．
【解析】根据能够完全重合的两个图形叫做全等形，重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角可得对应顶点，对应边与对应角，进而可得a，b，c，e，α各字母所表示的值．
解：对应顶点：A和G，E和F，D和J，C和I，B和H，
对应边：AB和GH，AE和GF，ED和FJ，CD和JI，BC和HI；
对应角：∠A和∠G，∠B和∠H，∠C和∠I，∠D和∠J，∠E和∠F；
∵两个五边形全等，
∴a=12，c=8，b=10，e=11，α=90°．
18．(1)3 ;(2)见解析.
【解析】分析：（1）根据全等三角形的性质得出AB＝DE＝8，BE＝BC＝5，即可求出答案；
（2）①根据全等三角形的性质得出∠A＝∠D＝35°，∠DBE＝∠C＝60°，根据三角形外角性质求出∠AEF，根据三角形外角性质求出∠AFD即可．
详解：（1）∵△ABC≌△DEB，DE＝8，BC＝5，
∴AB＝DE＝8，BE＝BC＝5，
∴AE＝AB BE＝8 5＝3，
故答案为：3；
(2)△ABC≌△DEB，
∴∠A=∠D=35°，∠DBE=∠C=60°，
∴∠AED=∠DBE+∠D=35°+60°=95°，
∴∠AFD=∠A+∠AED=130°
点睛：本题考查了全等三角形的性质，三角形外角性质的应用，能熟记全等三角形的性质是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
19．AB=2.
【解析】∵△ACF≌△DBE，∴AC=DB，
∴AC–BC=DB–BC，即AB=CD，
∵AD=11，BC=7，
∴AB=（AD–BC）=×（11–7）=2，
即AB=2．
20．∠AED＝95°，∠BFD＝105°，∠DGB＝70°.
【解析】分析：
根据“全等三角形的性质”和“三角形内角和定理及三角形外角的性质”结合已知条件进行分析解答即可.
详解：
∵△ABC≌△ADE，
∴∠EAD＝∠CAB.
∵∠CAD＝20°，∠EAB＝120°，
∴∠EAD＝∠CAB＝(∠EAB－∠CAD)＝50°.
∵∠D＋∠EAD＋∠AED＝180°，
∴∠AED＝180°－35°－50°＝95°.
∴∠FAB＝∠CAD＋∠CAB＝20°＋50°＝70°.
∴∠BFD＝∠B＋∠FAB＝35°＋70°＝105°.
∵∠BFD＝∠D＋∠DGB，
∴∠DGB＝∠BFD－∠D＝105°－35°＝70°.
点睛：本题是一道考查利用“全等三角形的性质、三角形内角和定理及三角形外角的性质”求角度的问题，熟悉“全等三角形的对应角相等，三角形的内角和为180°及三角形的一个外角等于与它不相邻的两个内角的和”等知识是解答本题的关键.
21．∠ACE＝90°
【解析】分析：根据全等三角形的性质可得∠BAC＝∠DCE，结合∠BAC＋∠BCA＝90°证∠DCE＋∠BCA＝90°.
详解：∠ACE＝90°.
理由：因为Rt△ABC≌Rt△CDE，
所以∠BAC＝∠DCE.
因为∠B＝90°，
所以∠BAC＋∠BCA＝90°.
所以∠DCE＋∠BCA＝90°.
所以∠ACE＝180°－(∠DCE＋∠BCA)＝90°.
点睛：本题考查了全等三角形的对应边相等，全等三角形的对应角相等，注意对应关系是关键．
22．见解析
【解析】试题分析：（1）根据全等三角形的对应边相等得到BD=BC=4.5cm，BE=AB=3cm，计算即可；
（2）根据全等三角形的对应角相等和平角的定义解答．
试题解析：解：（1）∵△ABD≌△EBC，∴BD=BC=4.5cm，BE=AB=3cm，∴DE=BD-BE=1.5cm；
（2）DB与AC垂直．理由如下：
∵△ABD≌△EBC，∴∠ABD=∠EBC．又∵A、B、C在一条直线上，∴∠EBC=90°，∴DB与AC垂直．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)