2.2 简单事件的概率(1)同步作业
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.2 简单事件的概率(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.小明做了 6 次掷质地均匀硬币的试验,在前 5 次试验中,有 2 次正面朝上,3 次正面朝下, 那么第 6 次试验,硬币正面朝上的概率是()
A. 1 B. 0 C. 0.5 D. 不稳定
2.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
A. B. C. D.
3.一个不透明的盒子里有9个黄球和若干个红球,红球和黄球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中红球的个数为( )
A. 11 B. 15 C. 19 D. 21
4.在一个不透明的袋子里装着9个完全相同的乒乓球,把它们分别标记上数字1,2,3,4,5,6,7,
8,9,从中随机摸出一个小球,标号为奇数的概率为
A. B. C. D.
5.在一个暗箱内放有a个除颜色外其余完全相同的小球,其中红球只有3个且摸到红球的概率为15%,则a的值是( )
A. 20 B. 15 C. 12 D. 9
6.四张相同的卡片,每张的正面分别写着,,,,将卡片正面朝下扣在桌上,随机抽出一张,这张卡片上写的不是最简二次根式的概率是( )
A. B. C. D.
7.小明向图中的格盘中随意掷一棋子,使之落在三角形内的概率是( )
A. B. C. D.
8.一个不透明的盒子中,放着编号为1到10的10张卡片(编号均为正整数),这些卡片除了编号以外没有任何其他区别.盒中卡片已经搅匀,从中随机的抽出一张卡片,则“该卡片上的数字大于”的概率是( )
A. B. C. D.
9.笔筒中有10支型号、颜色完全相同的铅笔,将它们逐一标上1﹣10的号码,若从笔筒中任意抽出一支铅笔,则抽到编号是3的倍数的概率是( )
A. B. C. D.
10.掷一枚均匀的骰子,骰子的6个面上分别刻有1、2、3、4、5、6点,则点数为奇数的概率是( )
A. B. C. D.
二、填空题
11.张华讲义夹里放了大小相同的试卷共12张,其中语文4张、数学2张、英语3张、物理3张,他随机地从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率为_______.
12.在一张边长为4cm的正方形纸上做扎针随机试验,纸上有一个半径为1cm的圆形阴影区域,则针头扎在阴影区域内的概率为__________;
13.袋子里有6只红球,4只白球,每只球除颜色以外都相同,从中任意摸出1只球,是红的可能性___________ 选填“大于”“小于”或“等于”)是白球的可能性.
14.有四张看上去无差别的卡片,正面分别写有“兴城首山”、“龙回头”、“觉华岛”、“葫芦山庄”四个景区的名称,将它们背面朝上,从中随机一张卡片正面写有“葫芦山庄”的概率是__.
15.已知函数y=(2k﹣1)x+4(k为常数),若从﹣3≤k≤3中任取k值,则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为_____.
16.如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
17.如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是__.
三、解答题
18.“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满100元,就会有一次转动大转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得20元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少?
19.有7张卡片,分别写有数字 -1,0,1,2,3,4,5,这七个数字,从中任意抽取一张,
(1)求抽到的数字为正数的概率
(2)求抽到数字的绝对值小于2的概率.
20.米奇家住宅面积为90平方米,其中客厅30平方米,大卧室18平方米,小卧室15平方米,厨房14平方米,大卫生间9平方米,小卫生间4平方米.如果一只小猫在该住宅内地面上任意跑.求:
(1)P(在客厅捉到小猫);
(2)P(在小卧室捉到小猫);
(3)P(在卫生间捉到小猫);
(4)P(不在卧室捉到小猫).
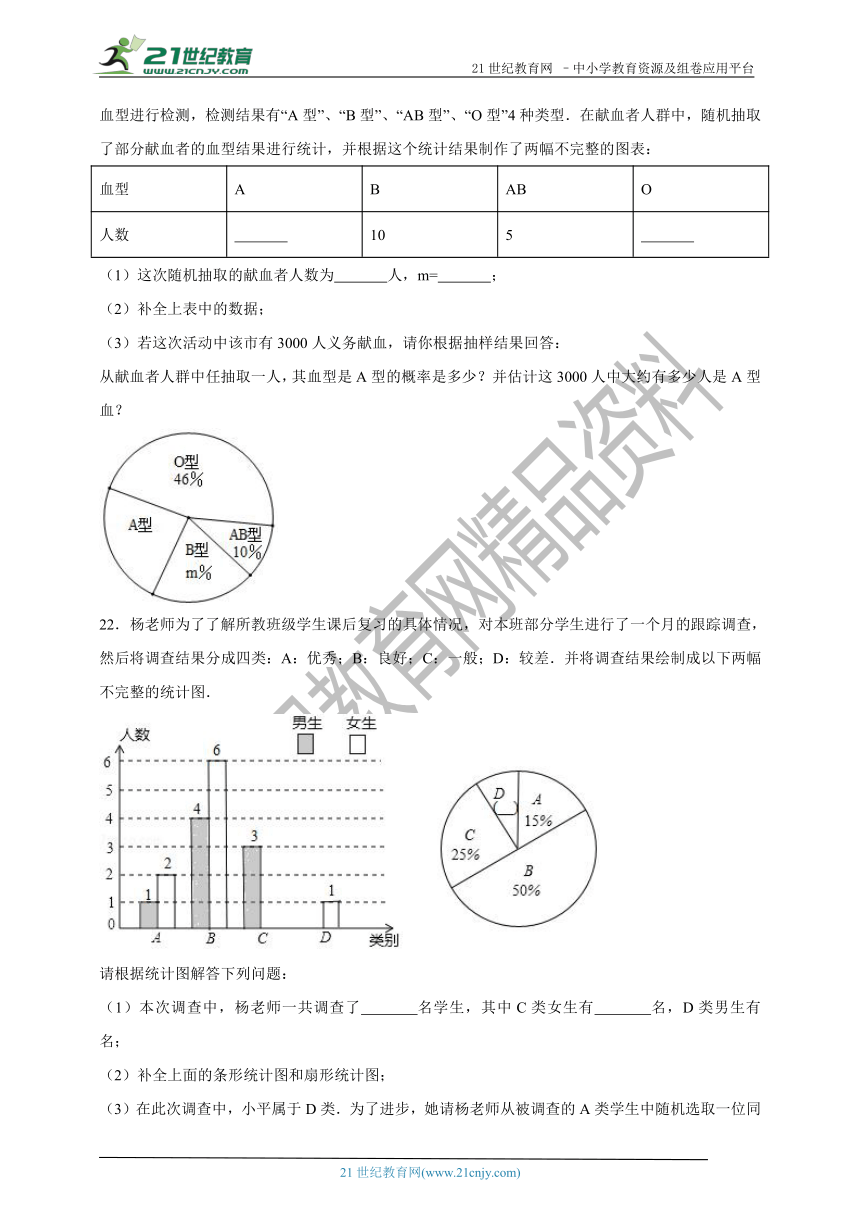
21.6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 A B AB O
人数 10 5
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?
22.杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.
请根据统计图解答下列问题:
(1)本次调查中,杨老师一共调查了 名学生,其中C类女生有 名,D类男生有 名;
(2)补全上面的条形统计图和扇形统计图;
(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.
参考答案
1.C
【解析】分析:本题是一道列举法求概率的问题,属于基础题,可以直接用概率的公式求解.
详解:因为一枚质地均匀的硬币只有正反两面,所以不管抛多少次,硬币正面朝上的概率都是.
故选C.
点睛:本题考查了概率的意义,一般地,在大量重复实验中,如果事件A发生的频率 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P( A) =p.明确概率的意义是解答的关键,用到的知识点为:概率=所求情况数与总情况数之比.
2.B
【解析】分析:根据题意可知所有的方块有15块,阴影方块有5块,根据概率的计算法则得出答案.
详解:P(停在阴影方砖)=,故选B.
点睛:本题主要考查的是概率的计算法则,属于基础题型.明确计算法则是解决这个问题的关键.
3.D
【解析】分析:
设盒子中红球的个数为x,根据题意列出方程,解方程即可求得红球的个数.
详解:
设盒子中红球的个数为x,根据题意得:
,
解得:,
经检验,是所列方程的解,
即盒子中红球大约有21个.
故选D.
点睛:知道在这一试验中:“摸到黄球的概率=袋子中黄球的个数:袋子中球的总数”是解答本题的关键.
4.C
【解析】分析:
由题意可知,从袋子中随机摸出一个球,共有9种等可能结果,其中标号为奇数的有1、3、5、7、9,共5种,由此即可得到所求概率.
详解:
∵从袋子中随机摸出一个球,其上的标号共有9种等可能结果,其中属于奇数的有1、3、5、7、9,共5种,
∴P(随机摸出一个球,标号刚好是奇数)=.
故选C.
点睛:读懂题意,知道随机从袋子中摸出一个球,其上的标号有9种等可能结果,其中属于奇数的有5种,是正确解答本题的关键.
5.A
【解析】分析:由在一个暗箱内放有a个除颜色外其余完全相同的小球,其中红球只有3个且摸到红球的概率为15%,根据概率公式即可得方程:=15%,解此方程即可求得答案.
详解:根据题意得: =15%,
解得:a=20.
故选A.
点睛:本题考查了概率公式.
6.A
【解析】分析:由,,,中,不是最简二次根式的只有,再用概率公式计算可得.
详解:
∵,,,中,不是最简二次根式的只有,
∴所以卡片上写的不是最简二次根式的概率是,
故选A.
点睛:考查了概率公式,掌握概率=所求情况数与总情况数之比和最简二次根式的定义是解题的关键.
7.C
【解析】【分析】先设小正方形的边长为1,求正方形和三角形的面积分别为9和3,再用面积比求概率.
【详解】设小正方形的边长为1,则正方形的面积为9,三角形的面积为,所以,棋子落在三角形内的概率是.
故选:C.
【点睛】本题考核知识点:几何概率. 解题关键点:本题将概率的求解设置于两种图形中,考查学生对简单几何概念的掌握情况,用到的知识点为:概率=相应的面积与总面积之比.
8.A
【解析】∵1到10的10张卡片中,大于的数有:6,7,8,9,10,
∴“该卡片上的数字大于”的概率是.
故选A.
9.C
【解析】【分析】由标有1﹣10的号码的10支铅笔中,标号为3的倍数的有3、6、9这3种情况,利用概率公式计算可得.
【详解】∵在标有1﹣10的号码的10支铅笔中,
标号为3的倍数的有3、6、9这3种情况,
∴抽到编号是3的倍数的概率是,
故选C.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
10.C
【解析】分析:根据题意和题目中的数据可以求得点数为奇数的概率.
详解:由题意可得,
点数为奇数的概率是:,
故选:C.
点睛:本题考查概率公式,解答本题的关键是明确题意,利用概率的知识解答.
11.
【解析】分析: 根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
详解: : ∵小明的讲义夹里放了大小相同的试卷共12张,其中数学2张,
∴他随机地从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率为 .
故答案为: .
点睛: 本题考查概率公式,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率.
12.
【解析】分析:
根据“所求概率=圆形阴影区域的面积和正方形纸片的面积之比”结合题中所给数据进行计算即可.
详解:
由题意可得:
P(针头扎在阴影区域)=.
故答案为:.
点睛:知道“针头扎在阴影区域内的概率=圆形阴影区域的面积和正方形纸片的面积之比”是解答本题的关键.
13.大于
【解析】试题分析:摸出红球的概率=6÷(6+4)=0.6,摸出是白球的概率=4÷(6+4)=0.4,则摸出是红球的可能性大于白球的可能性.
14.
【解析】【分析】共有4种可能,符合条件的有1种,利用概率公式进行计算即可得.
【详解】∵在这4张无差别的卡片上,只有1张写有“葫芦山庄”,
∴从中随机一张卡片正面写有“葫芦山庄”的概率是,
故答案为:.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
15.
【解析】【分析】直接利用一次函数增减性结合k的取值范围进而得出答案.
【详解】当2k﹣1>0时,
解得:k>,则<k≤3时,y随x增加而增加,
故﹣3≤k<时,y随x增加而减小,
则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为:,
故答案为:.
【点睛】本题考查了概率公式以及一次函数的性质,熟练掌握概率的计算方法以及一次函数的性质是解题的关键.
16.
【解析】【分析】根据几何概型概率的求法,飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比,根据题意,可得小正方形的面积与大正方形的面积,进而可得答案.
【详解】根据题意,AB2=AE2+BE2=13,
∴S正方形ABCD=13,
∵△ABE≌△BCF,
∴AE=BF=3,∵BE=2,
∴EF=1,
∴S正方形EFGH=1,
,故飞镖扎在小正方形内的概率为,
故答案为:.
【点睛】本题考查了几何概率的计算,求出小正方形的面积与大正方形的面积是解题的关键.
17.
【解析】分析:根据图形分析可得求图中阴影部分面积实为求扇形部分面积,而扇形面积是圆面积的,可得结论.
详解:如图所示:连接OA,
∵正六边形内接于⊙O,
∴△OAB,△OBC都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OC∥AB,
∴S△ABC=S△OBC,
∴S阴=S扇形OBC,
则飞镖落在阴影部分的概率是;
故答案为:.
点睛:此题主要考查了正多边形和圆、几何概率以及扇形面积求法,得出阴影部分面积=S扇形OBC是解题关键.
18.(1) (2) (3) (4)
【解析】【分析】从圆心角的度数可以算出每个扇形的面积与圆面积的比,这个比就是对应的奖项的概率.
【详解】解:(1)享受七折优惠的概率为;
(2)得20元的概率为;
(3)得10元的概率为;
(4) 中奖得钱的概率是.
【点睛】本题考核知识点:几何概率. 解题关键点:把事件的概率转化为扇形面积和圆的面积的比. 用到的知识点为:概率=相应的面积与总面积之比.
19.(1)抽到的数字为正数的概率为: ;(2)抽到的数字的绝对值小于2的概率为:
【解析】分析:根据概率公式解答即可.
详解:(1)-1,0,1,2,3,4,5中,正数为1,2,3,4,5,抽到数字为正数的概率为:P(正数)=;
(2)-1,0,1,2,3,4,5中,绝对值小于2的数有±1,0,抽到绝对值小于2的数的概率为:P(绝对值小于2)=.
点睛:本题考查了概率公式,熟悉古典概率是解题的关键.
20.(1) (2) (3) (4)
【解析】分析:
根据题意,由相应房间的面积比上总面积90进行计算即可.
详解:
由题意可得:
(1)P(在客厅捉到小猫)=;
(2)P(在小卧室捉到小猫)=;
(3)P(在卫生间捉到小猫)=;
(4)P(不在卧室捉到小猫)=.
点睛:知道:“在某个房间捉到小猫的概率=该房间的面积:米奇家住宅的总面积”是解答本题的关键.
21.(1)50,20;(2)12,23;见图;(3)大约有720人是A型血.
【解析】【分析】(1)用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数,然后用B型的人数除以抽取的总人数即可求得m的值;
(2)先计算出O型的人数,再计算出A型人数,从而可补全上表中的数据;
(3)用样本中A型的人数除以50得到血型是A型的概率,然后用3000乘以此概率可估计这3000人中是A型血的人数.
【详解】(1)这次随机抽取的献血者人数为5÷10%=50(人),
所以m=×100=20,
故答案为50,20;
(2)O型献血的人数为46%×50=23(人),
A型献血的人数为50﹣10﹣5﹣23=12(人),
补全表格中的数据如下:
血型 A B AB O
人数 12 10 5 23
故答案为12,23;
(3)从献血者人群中任抽取一人,其血型是A型的概率=,
3000×=720,
估计这3000人中大约有720人是A型血.
【点睛】本题考查了扇形统计图、统计表、概率公式、用样本估计总体等,读懂统计图、统计表,从中找到必要的信息是解题的关键;随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.
22.(1)20、2、1;(2)补图见解析;(3)
【解析】分析:(1)由A类别人数及其所占百分比可得总人数,用总人数乘以C类别百分比,再减去其中男生人数可得女生人数,同理求得D类别男生人数;
(2)根据(1)中所求结果可补全图形;
(3)根据概率公式计算可得.
详解:(1)杨老师调查的学生总人数为(1+2)÷15%=20人,
C类女生人数为20×25%-3=2人,D类男生人数为20×(1-15%-20%-25%)-1=1人,
故答案为:20、2、1;
(2)补全图形如下:
(3)因为A类的3人中,女生有2人,
所以所选的同学恰好是一位女同学的概率为.
点睛:此题考查了概率公式的应用以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.2 简单事件的概率(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.小明做了 6 次掷质地均匀硬币的试验,在前 5 次试验中,有 2 次正面朝上,3 次正面朝下, 那么第 6 次试验,硬币正面朝上的概率是()
A. 1 B. 0 C. 0.5 D. 不稳定
2.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
A. B. C. D.
3.一个不透明的盒子里有9个黄球和若干个红球,红球和黄球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中红球的个数为( )
A. 11 B. 15 C. 19 D. 21
4.在一个不透明的袋子里装着9个完全相同的乒乓球,把它们分别标记上数字1,2,3,4,5,6,7,
8,9,从中随机摸出一个小球,标号为奇数的概率为
A. B. C. D.
5.在一个暗箱内放有a个除颜色外其余完全相同的小球,其中红球只有3个且摸到红球的概率为15%,则a的值是( )
A. 20 B. 15 C. 12 D. 9
6.四张相同的卡片,每张的正面分别写着,,,,将卡片正面朝下扣在桌上,随机抽出一张,这张卡片上写的不是最简二次根式的概率是( )
A. B. C. D.
7.小明向图中的格盘中随意掷一棋子,使之落在三角形内的概率是( )
A. B. C. D.
8.一个不透明的盒子中,放着编号为1到10的10张卡片(编号均为正整数),这些卡片除了编号以外没有任何其他区别.盒中卡片已经搅匀,从中随机的抽出一张卡片,则“该卡片上的数字大于”的概率是( )
A. B. C. D.
9.笔筒中有10支型号、颜色完全相同的铅笔,将它们逐一标上1﹣10的号码,若从笔筒中任意抽出一支铅笔,则抽到编号是3的倍数的概率是( )
A. B. C. D.
10.掷一枚均匀的骰子,骰子的6个面上分别刻有1、2、3、4、5、6点,则点数为奇数的概率是( )
A. B. C. D.
二、填空题
11.张华讲义夹里放了大小相同的试卷共12张,其中语文4张、数学2张、英语3张、物理3张,他随机地从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率为_______.
12.在一张边长为4cm的正方形纸上做扎针随机试验,纸上有一个半径为1cm的圆形阴影区域,则针头扎在阴影区域内的概率为__________;
13.袋子里有6只红球,4只白球,每只球除颜色以外都相同,从中任意摸出1只球,是红的可能性___________ 选填“大于”“小于”或“等于”)是白球的可能性.
14.有四张看上去无差别的卡片,正面分别写有“兴城首山”、“龙回头”、“觉华岛”、“葫芦山庄”四个景区的名称,将它们背面朝上,从中随机一张卡片正面写有“葫芦山庄”的概率是__.
15.已知函数y=(2k﹣1)x+4(k为常数),若从﹣3≤k≤3中任取k值,则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为_____.
16.如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
17.如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是__.
三、解答题
18.“十一”黄金周期间,某购物广场举办迎国庆有奖销售活动,每购物满100元,就会有一次转动大转盘的机会,请你根据大转盘(如图)来计算:
(1)享受七折优惠的概率;
(2)得20元的概率;
(3)得10元的概率;
(4)中奖得钱的概率是多少?
19.有7张卡片,分别写有数字 -1,0,1,2,3,4,5,这七个数字,从中任意抽取一张,
(1)求抽到的数字为正数的概率
(2)求抽到数字的绝对值小于2的概率.
20.米奇家住宅面积为90平方米,其中客厅30平方米,大卧室18平方米,小卧室15平方米,厨房14平方米,大卫生间9平方米,小卫生间4平方米.如果一只小猫在该住宅内地面上任意跑.求:
(1)P(在客厅捉到小猫);
(2)P(在小卧室捉到小猫);
(3)P(在卫生间捉到小猫);
(4)P(不在卧室捉到小猫).
21.6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 A B AB O
人数 10 5
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?
22.杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.
请根据统计图解答下列问题:
(1)本次调查中,杨老师一共调查了 名学生,其中C类女生有 名,D类男生有 名;
(2)补全上面的条形统计图和扇形统计图;
(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.
参考答案
1.C
【解析】分析:本题是一道列举法求概率的问题,属于基础题,可以直接用概率的公式求解.
详解:因为一枚质地均匀的硬币只有正反两面,所以不管抛多少次,硬币正面朝上的概率都是.
故选C.
点睛:本题考查了概率的意义,一般地,在大量重复实验中,如果事件A发生的频率 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P( A) =p.明确概率的意义是解答的关键,用到的知识点为:概率=所求情况数与总情况数之比.
2.B
【解析】分析:根据题意可知所有的方块有15块,阴影方块有5块,根据概率的计算法则得出答案.
详解:P(停在阴影方砖)=,故选B.
点睛:本题主要考查的是概率的计算法则,属于基础题型.明确计算法则是解决这个问题的关键.
3.D
【解析】分析:
设盒子中红球的个数为x,根据题意列出方程,解方程即可求得红球的个数.
详解:
设盒子中红球的个数为x,根据题意得:
,
解得:,
经检验,是所列方程的解,
即盒子中红球大约有21个.
故选D.
点睛:知道在这一试验中:“摸到黄球的概率=袋子中黄球的个数:袋子中球的总数”是解答本题的关键.
4.C
【解析】分析:
由题意可知,从袋子中随机摸出一个球,共有9种等可能结果,其中标号为奇数的有1、3、5、7、9,共5种,由此即可得到所求概率.
详解:
∵从袋子中随机摸出一个球,其上的标号共有9种等可能结果,其中属于奇数的有1、3、5、7、9,共5种,
∴P(随机摸出一个球,标号刚好是奇数)=.
故选C.
点睛:读懂题意,知道随机从袋子中摸出一个球,其上的标号有9种等可能结果,其中属于奇数的有5种,是正确解答本题的关键.
5.A
【解析】分析:由在一个暗箱内放有a个除颜色外其余完全相同的小球,其中红球只有3个且摸到红球的概率为15%,根据概率公式即可得方程:=15%,解此方程即可求得答案.
详解:根据题意得: =15%,
解得:a=20.
故选A.
点睛:本题考查了概率公式.
6.A
【解析】分析:由,,,中,不是最简二次根式的只有,再用概率公式计算可得.
详解:
∵,,,中,不是最简二次根式的只有,
∴所以卡片上写的不是最简二次根式的概率是,
故选A.
点睛:考查了概率公式,掌握概率=所求情况数与总情况数之比和最简二次根式的定义是解题的关键.
7.C
【解析】【分析】先设小正方形的边长为1,求正方形和三角形的面积分别为9和3,再用面积比求概率.
【详解】设小正方形的边长为1,则正方形的面积为9,三角形的面积为,所以,棋子落在三角形内的概率是.
故选:C.
【点睛】本题考核知识点:几何概率. 解题关键点:本题将概率的求解设置于两种图形中,考查学生对简单几何概念的掌握情况,用到的知识点为:概率=相应的面积与总面积之比.
8.A
【解析】∵1到10的10张卡片中,大于的数有:6,7,8,9,10,
∴“该卡片上的数字大于”的概率是.
故选A.
9.C
【解析】【分析】由标有1﹣10的号码的10支铅笔中,标号为3的倍数的有3、6、9这3种情况,利用概率公式计算可得.
【详解】∵在标有1﹣10的号码的10支铅笔中,
标号为3的倍数的有3、6、9这3种情况,
∴抽到编号是3的倍数的概率是,
故选C.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
10.C
【解析】分析:根据题意和题目中的数据可以求得点数为奇数的概率.
详解:由题意可得,
点数为奇数的概率是:,
故选:C.
点睛:本题考查概率公式,解答本题的关键是明确题意,利用概率的知识解答.
11.
【解析】分析: 根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
详解: : ∵小明的讲义夹里放了大小相同的试卷共12张,其中数学2张,
∴他随机地从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率为 .
故答案为: .
点睛: 本题考查概率公式,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率.
12.
【解析】分析:
根据“所求概率=圆形阴影区域的面积和正方形纸片的面积之比”结合题中所给数据进行计算即可.
详解:
由题意可得:
P(针头扎在阴影区域)=.
故答案为:.
点睛:知道“针头扎在阴影区域内的概率=圆形阴影区域的面积和正方形纸片的面积之比”是解答本题的关键.
13.大于
【解析】试题分析:摸出红球的概率=6÷(6+4)=0.6,摸出是白球的概率=4÷(6+4)=0.4,则摸出是红球的可能性大于白球的可能性.
14.
【解析】【分析】共有4种可能,符合条件的有1种,利用概率公式进行计算即可得.
【详解】∵在这4张无差别的卡片上,只有1张写有“葫芦山庄”,
∴从中随机一张卡片正面写有“葫芦山庄”的概率是,
故答案为:.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
15.
【解析】【分析】直接利用一次函数增减性结合k的取值范围进而得出答案.
【详解】当2k﹣1>0时,
解得:k>,则<k≤3时,y随x增加而增加,
故﹣3≤k<时,y随x增加而减小,
则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为:,
故答案为:.
【点睛】本题考查了概率公式以及一次函数的性质,熟练掌握概率的计算方法以及一次函数的性质是解题的关键.
16.
【解析】【分析】根据几何概型概率的求法,飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比,根据题意,可得小正方形的面积与大正方形的面积,进而可得答案.
【详解】根据题意,AB2=AE2+BE2=13,
∴S正方形ABCD=13,
∵△ABE≌△BCF,
∴AE=BF=3,∵BE=2,
∴EF=1,
∴S正方形EFGH=1,
,故飞镖扎在小正方形内的概率为,
故答案为:.
【点睛】本题考查了几何概率的计算,求出小正方形的面积与大正方形的面积是解题的关键.
17.
【解析】分析:根据图形分析可得求图中阴影部分面积实为求扇形部分面积,而扇形面积是圆面积的,可得结论.
详解:如图所示:连接OA,
∵正六边形内接于⊙O,
∴△OAB,△OBC都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OC∥AB,
∴S△ABC=S△OBC,
∴S阴=S扇形OBC,
则飞镖落在阴影部分的概率是;
故答案为:.
点睛:此题主要考查了正多边形和圆、几何概率以及扇形面积求法,得出阴影部分面积=S扇形OBC是解题关键.
18.(1) (2) (3) (4)
【解析】【分析】从圆心角的度数可以算出每个扇形的面积与圆面积的比,这个比就是对应的奖项的概率.
【详解】解:(1)享受七折优惠的概率为;
(2)得20元的概率为;
(3)得10元的概率为;
(4) 中奖得钱的概率是.
【点睛】本题考核知识点:几何概率. 解题关键点:把事件的概率转化为扇形面积和圆的面积的比. 用到的知识点为:概率=相应的面积与总面积之比.
19.(1)抽到的数字为正数的概率为: ;(2)抽到的数字的绝对值小于2的概率为:
【解析】分析:根据概率公式解答即可.
详解:(1)-1,0,1,2,3,4,5中,正数为1,2,3,4,5,抽到数字为正数的概率为:P(正数)=;
(2)-1,0,1,2,3,4,5中,绝对值小于2的数有±1,0,抽到绝对值小于2的数的概率为:P(绝对值小于2)=.
点睛:本题考查了概率公式,熟悉古典概率是解题的关键.
20.(1) (2) (3) (4)
【解析】分析:
根据题意,由相应房间的面积比上总面积90进行计算即可.
详解:
由题意可得:
(1)P(在客厅捉到小猫)=;
(2)P(在小卧室捉到小猫)=;
(3)P(在卫生间捉到小猫)=;
(4)P(不在卧室捉到小猫)=.
点睛:知道:“在某个房间捉到小猫的概率=该房间的面积:米奇家住宅的总面积”是解答本题的关键.
21.(1)50,20;(2)12,23;见图;(3)大约有720人是A型血.
【解析】【分析】(1)用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数,然后用B型的人数除以抽取的总人数即可求得m的值;
(2)先计算出O型的人数,再计算出A型人数,从而可补全上表中的数据;
(3)用样本中A型的人数除以50得到血型是A型的概率,然后用3000乘以此概率可估计这3000人中是A型血的人数.
【详解】(1)这次随机抽取的献血者人数为5÷10%=50(人),
所以m=×100=20,
故答案为50,20;
(2)O型献血的人数为46%×50=23(人),
A型献血的人数为50﹣10﹣5﹣23=12(人),
补全表格中的数据如下:
血型 A B AB O
人数 12 10 5 23
故答案为12,23;
(3)从献血者人群中任抽取一人,其血型是A型的概率=,
3000×=720,
估计这3000人中大约有720人是A型血.
【点睛】本题考查了扇形统计图、统计表、概率公式、用样本估计总体等,读懂统计图、统计表,从中找到必要的信息是解题的关键;随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.
22.(1)20、2、1;(2)补图见解析;(3)
【解析】分析:(1)由A类别人数及其所占百分比可得总人数,用总人数乘以C类别百分比,再减去其中男生人数可得女生人数,同理求得D类别男生人数;
(2)根据(1)中所求结果可补全图形;
(3)根据概率公式计算可得.
详解:(1)杨老师调查的学生总人数为(1+2)÷15%=20人,
C类女生人数为20×25%-3=2人,D类男生人数为20×(1-15%-20%-25%)-1=1人,
故答案为:20、2、1;
(2)补全图形如下:
(3)因为A类的3人中,女生有2人,
所以所选的同学恰好是一位女同学的概率为.
点睛:此题考查了概率公式的应用以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
