1.5 全等三角形的判定(1)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 1.5 全等三角形的判定(1)(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | doc | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-05 21:17:51 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
浙江版八年级数学上册第一章1.5全等三角形的判定
第1课时 全等三角形的判定(1)
【知识清单】
1.全等三角形判定1:三边对应相等的两个三角形全等(简称“边边边”或“SSS”) ;
2.三角形的稳定性:当三角形的三条边确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
3.证明两个三角形全等的过程的一般格式:(1)准备条件:把题中没有直接给出的相等条件证明出来,一般由线段的中点、两条线段的和或差、等量代换获得;(2)确定范围:在哪两个三角形中;(3)摆齐条件:把要证明的两个三角形全等的所需的三组条件按顺序摆好,并用大括号括在一起,注意对应元素放在对应位置上,依据写在每一步后面的括号内(如下图);(4)得出结论:得出三角形全等的结论.
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
4.方法技巧:(1)证明两条线段相等和两个角相等可以通过两个三角形全等来实现;
(2)要充分挖掘隐含条件,如公共边、边的中点等;
(3)要抓住图形特征,有时需要运用等式的性质找出证明三角形全等缺少的相等的条件,从而实现两个三角形全等;
(4)巧妙作出辅助线,沟通图形的关系,为证明打开通道.
5.考点:证明三角形全等,以及在三角形全等的基础之上进一步证明线段、角度之间的数量关系.
【经典例题】
例题1,如图,若点B、F、C、E在同一条直线上,AB=DE,BF=EC,AC=DF,∠B=62°, ∠DFE=31°,求∠A的度数.
【解析】先证明BC=EF,再运用“SSS”证明△ABC≌△DEF,进而可得∠ACB=∠DFE=31°,在△ABC中根据三角形内角和定理可求∠A的度数,从而可得结论.
【详解】∵BF=EC(已知),
∴BC=BF+FC,EF=EC+CF(等式的性质),
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠ACB=∠DFE=31°(全等三角形对应角相等).
∵∠B=62°(已知),
∴∠A=180°-(∠B+∠ACB)=180°-(62°+31°)=87°(三角形内角和定理).
【点评】本题考查三角形全等的判定方法“SSS”公理和三角形内角和定理,证明BC=EF是解决问题的关键.
例题2,如图所示,BC=ED,BD=EC,求证:BC∥DE. 请你给下面的每一步填上依据.
【分析】因为四边形BCED中没有三角形,所以应该先构造三角形,就需要作辅助线,连接CD或BE皆可,再运用“SSS” 证明△BCD≌△EDC,从而得出∠B=∠E.
【详解】连接CD,
在△BCD和△EDC中,
∴△BCD≌△EDC(SSS).
∴∠BCD=∠EDC(全等三角形的对应角相等).
∴BC∥DE(内错角相等两直线平行).
【点评】本题考查三角形全等的判定方法“SSS”公理和平行线的判定.作辅助线构造全等三角形是解决问题的关键.
【夯实基础】
1.不是利用三角形稳定性的是( )
A.自行车的三角形车架 B.三角形房架 C.照相机的三角架 D.矩形门框的斜拉条
2.如图,点E是BD的中点,AB=AD,BC=DC,图中全等三角形有( )
A.4对 B.3对 C.2对 D.1对
3.如图,点E,D分别在AB,AC上,若AB=AC,BE=CD,BD=EC,∠B=32°,∠A=41°,
则∠BOC度数是( )
A.135° B.125° C.115° D.105°
4.在△ABC中,已知AB=AC,AD是BC边上的中线,则∠ADC是( )
A. 直角 B. 锐角 C. 钝角 D.不能确定
5.如图,有一个简易平分角的仪器,其中AB=AD,BC=DC,将A点放在角的顶点处,AB和AD沿着角的两边张开,沿对角线AC画射线AE,AE就是∠BAD的平分线,这个平分角的仪器能平分角的原理是 .
6.如图,AB=AD,根据“SSS”判定△ABC≌△ADC,则需要补充的一个条件是 .
7.如图,点C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
【提优特训】
8.如图,木工师傅用4根木条钉成一个四边形木架ABCD,要使这个木架不变形,木工师傅至少要再钉上木条( )
A.4根 B.3根 C.2根 D.1根
9.如图,AB=AC,AD=AE,BE=CD,则△ABE≌ ,△ABD≌ .
10.如图,已知AB=DC,AC=DB,要想证明∠A=∠D,根据现有的知识你能添加的辅助线是,连接 .
11. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是_.
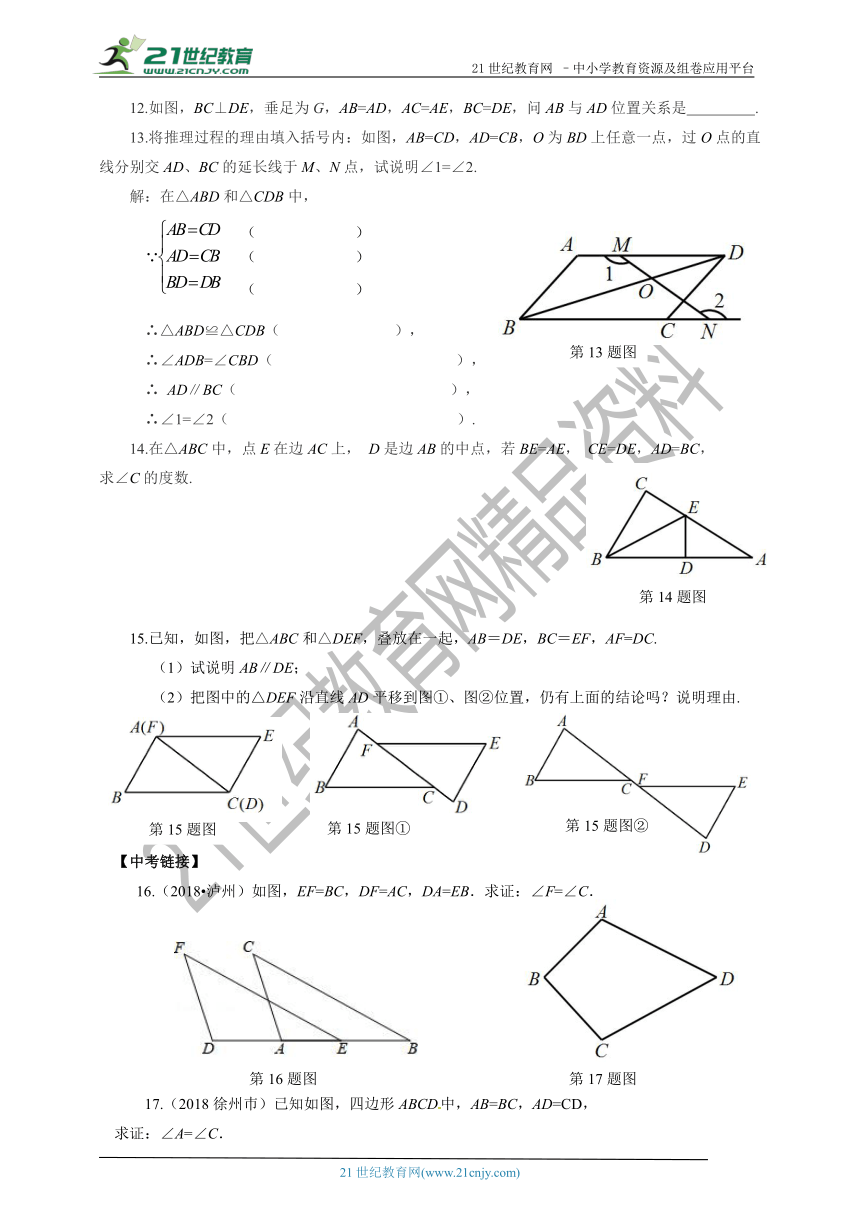
12.如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问AB与AD位置关系是 .
13.将推理过程的理由填入括号内:如图,AB=CD,AD=CB,O为BD上任意一点,过O点的直线分别交AD、BC的延长线于M、N点,试说明∠1=∠2.
解:在△ABD和△CDB中,
∴△ABD≌△CDB( ),
∴∠ADB=∠CBD( ),
∴ AD∥BC( ),
∴∠1=∠2( ).
14.在△ABC中,点E在边AC上, D是边AB的中点,若BE=AE, CE=DE,AD=BC,
求∠C的度数.
15.已知,如图,把△ABC和△DEF,叠放在一起,AB=DE,BC=EF,AF=DC.
(1)试说明AB∥DE;
(2)把图中的△DEF沿直线AD平移到图①、图②位置,仍有上面的结论吗?说明理由.
【中考链接】
16.(2018 泸州)如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
17.(2018徐州巿)已知如图,四边形ABCD中,AB=BC,AD=CD,
求证:∠A=∠C.
18.(2018桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌ΔDEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.C 2.B 3.D 4.A 5.SSS 6.BC=DC 8.D 9. ΔACD 、ΔACE 10.BC 11. SSS
12.AB⊥AD.
7.证明:∵点C是AE的中点(已知),
∴AC=CE(中点定义).
在△ABC和△CDE中,
∵
∴△ABC≌△CDE(SSS),
∴∠A=∠ECD(全等三角形对应角相等).
∴ AB∥CD( 同位角相等两直线平行).
13.解:在△ABD和△CDB中,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD(全等三角形对应角相等),
∴ AD∥BC(内错角相等两直线平行 ),
∴∠1=∠2( 两直线平行内错角相等).
14.【答案】∠C=90°
【分析】由D是边AB的中点,可得BD=AD,运用“SSS”公理证明△BED≌△AED,从而得出∠BDE=90°,再运用“SSS”公理证明△BCE≌△BED,便可得出∠C=∠BDE =90°的结论.
【详解】 ∵D是边AB的中点(已知),
∴BD=AD(中点定义).
在△BED和△AED中,
∴△BED≌△AED(SSS).
∴∠BDE=∠ADE(全等三角形对应角相等).
∵∠BDE+∠ADE=180°(平角定义),
∴∠BDE=∠ADE=90°.
∵BD=AD(已证),AD=BC(已知)
∴BD=BC(等量代换)
在△BED和△BEC中,
∴△BED≌△BEC(SSS).
∴∠C=∠BDE =90°(等量代换).
【点评】本题考查三角形全等的判定方法“SSS”公理,并且是两次使用“SSS”公理.中点定义和公共边的使用是解决问题的关键.
15.证明:(1)如图,在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠BAC=∠EDF(全等三角形对应角相等).
∴AB∥DE(内错角相等两直线平行).
(2)上面的结论仍成立,图①、图②中,由AF=DC,可得AC=DF,以下证明过程同(1).
16.【考点】全等三角形的判定与性质.
【专题】三角形.
【分析】欲证明∠F=∠C,只要证明△ABC≌△DEF(SSS)即可;
【解答】证明:∵DA=EB,
∴DE=DA+AE,AB=AE+EB.
即DE=AB,
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠C=∠F.
【点评】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定方法,属于中考基础题目.
17.【分析】(A类)连接BD,由AB=AC、AD=CD、BD=BD知ΔABD≌ΔCBD,∠A=∠C.
【解答】证明:连接BD,
在△ABD和△CBD中,
∴△ABD和△CBD(SSS)
∴∠A=∠C(全等三角形对应角相等).
【点评】本题主要考查等腰三角形的判定与性质,解题的关键是掌握等角对等边、等边对等角的性质.
18.【答案】(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
【详解】(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
【点评】本题考查三角形全等的判定方法SSS公理,证明AC=DF是解决问题的关键.
例题1图
例题2图
例题2图
第2题图
第3题图
第5题图
第7题图
第6题图
第9题图
第8题图
第10题图
第12题图
第11题图
第13题图
( )
( )
( )
第14题图
第15题图②
第15题图①
第15题图
第17题图
第16题图
第18题图
第7题图
第13题图
第14题图
第15题图
第15题图①
第15题图②
第16题图
第17题图
第18题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江版八年级数学上册第一章1.5全等三角形的判定
第1课时 全等三角形的判定(1)
【知识清单】
1.全等三角形判定1:三边对应相等的两个三角形全等(简称“边边边”或“SSS”) ;
2.三角形的稳定性:当三角形的三条边确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
3.证明两个三角形全等的过程的一般格式:(1)准备条件:把题中没有直接给出的相等条件证明出来,一般由线段的中点、两条线段的和或差、等量代换获得;(2)确定范围:在哪两个三角形中;(3)摆齐条件:把要证明的两个三角形全等的所需的三组条件按顺序摆好,并用大括号括在一起,注意对应元素放在对应位置上,依据写在每一步后面的括号内(如下图);(4)得出结论:得出三角形全等的结论.
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
4.方法技巧:(1)证明两条线段相等和两个角相等可以通过两个三角形全等来实现;
(2)要充分挖掘隐含条件,如公共边、边的中点等;
(3)要抓住图形特征,有时需要运用等式的性质找出证明三角形全等缺少的相等的条件,从而实现两个三角形全等;
(4)巧妙作出辅助线,沟通图形的关系,为证明打开通道.
5.考点:证明三角形全等,以及在三角形全等的基础之上进一步证明线段、角度之间的数量关系.
【经典例题】
例题1,如图,若点B、F、C、E在同一条直线上,AB=DE,BF=EC,AC=DF,∠B=62°, ∠DFE=31°,求∠A的度数.
【解析】先证明BC=EF,再运用“SSS”证明△ABC≌△DEF,进而可得∠ACB=∠DFE=31°,在△ABC中根据三角形内角和定理可求∠A的度数,从而可得结论.
【详解】∵BF=EC(已知),
∴BC=BF+FC,EF=EC+CF(等式的性质),
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠ACB=∠DFE=31°(全等三角形对应角相等).
∵∠B=62°(已知),
∴∠A=180°-(∠B+∠ACB)=180°-(62°+31°)=87°(三角形内角和定理).
【点评】本题考查三角形全等的判定方法“SSS”公理和三角形内角和定理,证明BC=EF是解决问题的关键.
例题2,如图所示,BC=ED,BD=EC,求证:BC∥DE. 请你给下面的每一步填上依据.
【分析】因为四边形BCED中没有三角形,所以应该先构造三角形,就需要作辅助线,连接CD或BE皆可,再运用“SSS” 证明△BCD≌△EDC,从而得出∠B=∠E.
【详解】连接CD,
在△BCD和△EDC中,
∴△BCD≌△EDC(SSS).
∴∠BCD=∠EDC(全等三角形的对应角相等).
∴BC∥DE(内错角相等两直线平行).
【点评】本题考查三角形全等的判定方法“SSS”公理和平行线的判定.作辅助线构造全等三角形是解决问题的关键.
【夯实基础】
1.不是利用三角形稳定性的是( )
A.自行车的三角形车架 B.三角形房架 C.照相机的三角架 D.矩形门框的斜拉条
2.如图,点E是BD的中点,AB=AD,BC=DC,图中全等三角形有( )
A.4对 B.3对 C.2对 D.1对
3.如图,点E,D分别在AB,AC上,若AB=AC,BE=CD,BD=EC,∠B=32°,∠A=41°,
则∠BOC度数是( )
A.135° B.125° C.115° D.105°
4.在△ABC中,已知AB=AC,AD是BC边上的中线,则∠ADC是( )
A. 直角 B. 锐角 C. 钝角 D.不能确定
5.如图,有一个简易平分角的仪器,其中AB=AD,BC=DC,将A点放在角的顶点处,AB和AD沿着角的两边张开,沿对角线AC画射线AE,AE就是∠BAD的平分线,这个平分角的仪器能平分角的原理是 .
6.如图,AB=AD,根据“SSS”判定△ABC≌△ADC,则需要补充的一个条件是 .
7.如图,点C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
【提优特训】
8.如图,木工师傅用4根木条钉成一个四边形木架ABCD,要使这个木架不变形,木工师傅至少要再钉上木条( )
A.4根 B.3根 C.2根 D.1根
9.如图,AB=AC,AD=AE,BE=CD,则△ABE≌ ,△ABD≌ .
10.如图,已知AB=DC,AC=DB,要想证明∠A=∠D,根据现有的知识你能添加的辅助线是,连接 .
11. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是_.
12.如图,BC⊥DE,垂足为G,AB=AD,AC=AE,BC=DE,问AB与AD位置关系是 .
13.将推理过程的理由填入括号内:如图,AB=CD,AD=CB,O为BD上任意一点,过O点的直线分别交AD、BC的延长线于M、N点,试说明∠1=∠2.
解:在△ABD和△CDB中,
∴△ABD≌△CDB( ),
∴∠ADB=∠CBD( ),
∴ AD∥BC( ),
∴∠1=∠2( ).
14.在△ABC中,点E在边AC上, D是边AB的中点,若BE=AE, CE=DE,AD=BC,
求∠C的度数.
15.已知,如图,把△ABC和△DEF,叠放在一起,AB=DE,BC=EF,AF=DC.
(1)试说明AB∥DE;
(2)把图中的△DEF沿直线AD平移到图①、图②位置,仍有上面的结论吗?说明理由.
【中考链接】
16.(2018 泸州)如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
17.(2018徐州巿)已知如图,四边形ABCD中,AB=BC,AD=CD,
求证:∠A=∠C.
18.(2018桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌ΔDEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.C 2.B 3.D 4.A 5.SSS 6.BC=DC 8.D 9. ΔACD 、ΔACE 10.BC 11. SSS
12.AB⊥AD.
7.证明:∵点C是AE的中点(已知),
∴AC=CE(中点定义).
在△ABC和△CDE中,
∵
∴△ABC≌△CDE(SSS),
∴∠A=∠ECD(全等三角形对应角相等).
∴ AB∥CD( 同位角相等两直线平行).
13.解:在△ABD和△CDB中,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD(全等三角形对应角相等),
∴ AD∥BC(内错角相等两直线平行 ),
∴∠1=∠2( 两直线平行内错角相等).
14.【答案】∠C=90°
【分析】由D是边AB的中点,可得BD=AD,运用“SSS”公理证明△BED≌△AED,从而得出∠BDE=90°,再运用“SSS”公理证明△BCE≌△BED,便可得出∠C=∠BDE =90°的结论.
【详解】 ∵D是边AB的中点(已知),
∴BD=AD(中点定义).
在△BED和△AED中,
∴△BED≌△AED(SSS).
∴∠BDE=∠ADE(全等三角形对应角相等).
∵∠BDE+∠ADE=180°(平角定义),
∴∠BDE=∠ADE=90°.
∵BD=AD(已证),AD=BC(已知)
∴BD=BC(等量代换)
在△BED和△BEC中,
∴△BED≌△BEC(SSS).
∴∠C=∠BDE =90°(等量代换).
【点评】本题考查三角形全等的判定方法“SSS”公理,并且是两次使用“SSS”公理.中点定义和公共边的使用是解决问题的关键.
15.证明:(1)如图,在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠BAC=∠EDF(全等三角形对应角相等).
∴AB∥DE(内错角相等两直线平行).
(2)上面的结论仍成立,图①、图②中,由AF=DC,可得AC=DF,以下证明过程同(1).
16.【考点】全等三角形的判定与性质.
【专题】三角形.
【分析】欲证明∠F=∠C,只要证明△ABC≌△DEF(SSS)即可;
【解答】证明:∵DA=EB,
∴DE=DA+AE,AB=AE+EB.
即DE=AB,
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠C=∠F.
【点评】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定方法,属于中考基础题目.
17.【分析】(A类)连接BD,由AB=AC、AD=CD、BD=BD知ΔABD≌ΔCBD,∠A=∠C.
【解答】证明:连接BD,
在△ABD和△CBD中,
∴△ABD和△CBD(SSS)
∴∠A=∠C(全等三角形对应角相等).
【点评】本题主要考查等腰三角形的判定与性质,解题的关键是掌握等角对等边、等边对等角的性质.
18.【答案】(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
【详解】(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
【点评】本题考查三角形全等的判定方法SSS公理,证明AC=DF是解决问题的关键.
例题1图
例题2图
例题2图
第2题图
第3题图
第5题图
第7题图
第6题图
第9题图
第8题图
第10题图
第12题图
第11题图
第13题图
( )
( )
( )
第14题图
第15题图②
第15题图①
第15题图
第17题图
第16题图
第18题图
第7题图
第13题图
第14题图
第15题图
第15题图①
第15题图②
第16题图
第17题图
第18题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
