第4章 代数式单元测试卷（含答案）

21世纪教育网 –中小学教育资源及组卷应用平台
第四章代数式单元测试卷
　
一．选择题（共10小题，满分30分，每小题3分）
1．代数式a2﹣的正确解释是（　　）
A．a与b的倒数的差的平方 B．a的平方与b的差的倒数
C．a的平方与b的倒数的差 D．a与b的差的平方的倒数
2．下列语句中错误的是（　　）
A．数字0也是单项式
B．单项式﹣a的系数与次数都是1
C．xy是二次单项式
D．﹣的系数是﹣
3．已知﹣2m6n与5m2xny是同类项，则（　　）
A．x=2，y=1 B．x=3，y=1 C． D．x=3，y=0
4．3x2y﹣5yx2=（　　）
A．不能运算 B．﹣2 C．﹣2yx2 D．﹣2xy
5．下列各式由等号左边变到右边变错的有（　　）
①a﹣（b﹣c）=a﹣b﹣c
②（x2+y）﹣2（x﹣y2）=x2+y﹣2x+y2
③﹣（a+b）﹣（﹣x+y）=﹣a+b+x﹣y
④﹣3（x﹣y）+（a﹣b）=﹣3x﹣3y+a﹣b．
A．1个 B．2个 C．3个 D．4个
6．代数式a+b2的意义是（　　）
A．a与b的和的平方 B．a与b两数的平方和
C．a与b的平方的和 D．a与b的平方
7．已知a＜b，那么a﹣b和它的相反数的差的绝对值是（　　）
A．b﹣a B．2b﹣2a C．﹣2a D．2b
8．下列定义一种关于n的运算：①当n是奇数时，结果为3n+5 ②n为偶数时结果是（其中k是使是奇数的正整数），并且运算重复进行．例如：取n=26，则…，若n=449，则第449次运算结果是（　　）
A．1 B．2 C．7 D．8
9．用一个正方形在四月份的日历上，圈出4个数，这四个数的和不可能是（　　）
A．104 B．108 C．24 D．28
10．如果x﹣y=5，y﹣z=5，那么z﹣x的值是（　　）
A．5 B．10 C．﹣5 D．﹣10　
二．填空题（共10小题，满分30分，每小题3分）
11．0.4xy3的系数是　 　，次数为　 　．
12．观察下面的一列单项式：x，﹣2x2，4x3，﹣8x4，…根据你发现的规律，第7个单项式为　 　；第n个单项式为　 　．
13．记x=（1+2）（1+22）（1+24）（1+28）…（1+2n），且x+1=2128，则n=　 　．
14．已知关于x的多项式（m﹣2）x2﹣mx+3中的x的一次项系数为﹣2，则这个多项式是　 　次　 　项式．
15．已知2axbn﹣1与同3a2b2m（m为正整数）是同类项，那么（2m﹣n）x=　 　．
16．若单项式﹣xm﹣2y3与xny2m﹣3n的和仍是单项式，则m﹣n=　 　．
17．学校决定修建一块长方形草坪，长为a米，宽为b米，并在草坪上修建如图所示的十字路，已知十字路宽x米，则草坪的面积是　 　平方米．
18．若4x+3y+5=0，则3（8y﹣x）﹣5（x+6y﹣2）的值等于　 　．
19．已知圆环内直径为acm，外直径为bcm，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为　 　cm．
20．观察等式：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…猜想：（1）1+3+5+7…+99=　 　；（2）1+3+5+7+…+（2n﹣1）=　 　．结果用含n的式子表示，其中n=1，2，3，…）．
三．解答题（共6小题，满分40分）
21．（6分）已知：M=3x2+2x﹣1，N=﹣x2﹣2+3x，求M﹣2N．
22．（6分）若（2x2+ax﹣y+b）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，试求a，b的值．
23．（6分）先化简，再求值：2（a2b+ab2）﹣2（a2b﹣1）﹣ab2﹣2．其中a=1，b=﹣3．
24．（6分）先化简再求值
2（a2b+ab2）﹣2（a2b﹣1）﹣ab2﹣2，其中a=2，b=﹣1．
25．（8分）某公司派出甲车前往某地完成任务，此时，有一辆流动加油车与他同时出发，且在同一条公路上匀速行驶（速度保持不变）．为了确定汽车的位置，我们用OX表示这条公路，原点O为零千米路标，并作如下约定：速度为正，表示汽车向数轴的正方向行驶；速度为负，表示汽车向数轴的负方向行驶；速度为零，表示汽车静止．行程为正，表示汽车位于零千米的右侧；行程为负，表示汽车位于零千米的左侧；行程为零，表示汽车位于零千米处．两车行程记录如表：
时间（h） 0 5 7 x
甲车位置（km） 190 ﹣10
流动加油车位置（km） 170 270
由上面表格中的数据，解决下列问题：
（1）甲车开出7小时时的位置为　 　km，流动加油车出发位置为　 　km；
（2）当两车同时开出x小时时，甲车位置为　 　km，流动加油车位置为　 　 km （用x的代数式表示）；
（3）甲车出发前由于未加油，汽车启动后司机才发现油箱内汽油仅够行驶3小时，问：甲车连续行驶3小时后，能否立刻获得流动加油车的帮助？请说明理由．
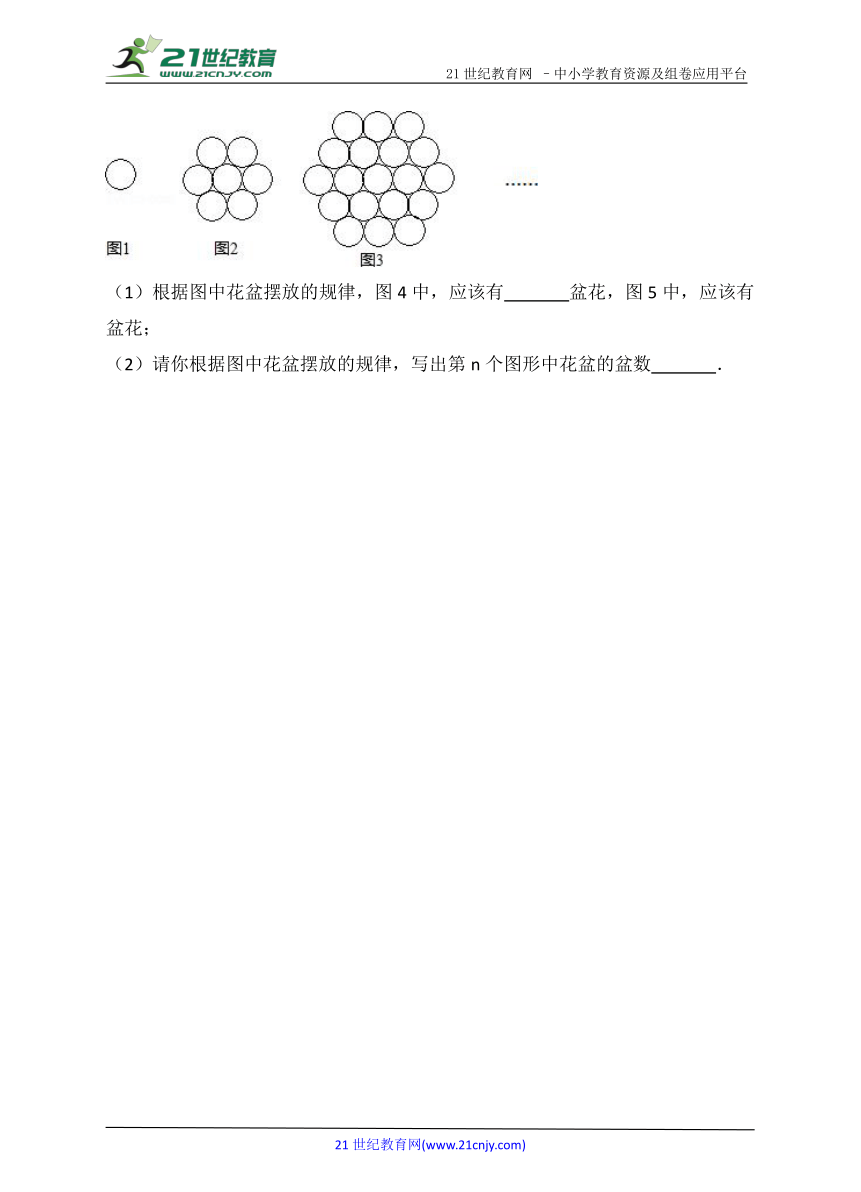
26．（8分）如图1，2，3，…是由花盆摆成的图案，图1中有1盆花，图2中有7盆花，图3中有19盆花，…
（1）根据图中花盆摆放的规律，图4中，应该有　 　盆花，图5中，应该有　 　盆花；
（2）请你根据图中花盆摆放的规律，写出第n个图形中花盆的盆数　 　．
　
参考答案与试题解析
　
一．选择题（共10小题，满分30分，每小题3分）
1．解：代数式a2﹣表示a的平方与b的倒数的差，
故选：C．
2．解：单独的一个数字也是单项式，故A正确；
单项式﹣a的系数应是﹣1，次数是1，故B错误；
xy的次数是2，符合单项式的定义，故C正确；
﹣的系数是﹣，故D正确．
故选：B．
3．解：由同类项的定义可知
2x=6，x=3；y=1．
故选：B．
4．解：3x2y﹣5yx2=﹣2yx2
故选：C．
5．解：根据去括号的法则：
①应为a﹣（b﹣c）=a﹣b+c，错误；
②应为（x2+y）﹣2（x﹣y2）=x2+y﹣2x+2y2，错误；
③应为﹣（a+b）﹣（﹣x+y）=﹣a﹣b+x﹣y，错误；
④﹣3（x﹣y）+（a﹣b）=﹣3x+3y+a﹣b，错误．
故选：D．
6．解：代数式a+b2的意义是a与b的平方的和．
故选：C．
7．解：依题意可得：|（a﹣b）﹣（b﹣a）|=2b﹣2a．故选B．
8．解：第一次：3×449+5=1352，
第二次：，根据题意k=3时结果为169；
第三次：3×169+5=512，
第四次：因为512是2的9次方，所以k=9，计算结果是1；
第五次：1×3+5=8；
第六次：，因为8是2的3次方，所以k=3，计算结果是1，此后计算结果8和1循环．
因为449是奇数，所以第449次运算结果是8．
故选：D．
9．解：设最小的代数式是x，则其它三个数分别是x+1，x+7，x+8，
四数之和=x+x+1+x+7+x+8=4x+16．
A、根据题意得4x+16=104，解得x=22，正确；
B、根据题意得4x+16=108，解得x=23，而x+8=31，因为四月份只有30天，不合实际意义，故不正确；
C、根据题意得4x+16=24，解得x=2，正确；
D、根据题意得4x+16=28，解得x=3，正确．
故选：B．
10．解：∵x﹣y=5，y﹣z=5，
∴（x﹣y）+（y﹣z）=x﹣z=10，
∴z﹣x=﹣10．
故选：D．
二．填空题（共10小题，满分30分，每小题3分）
11．解：∵单项式0.4xy3的数字因数是0.4，所有字母指数的和=1+3=4，
∴此单项式的系数是0.4，次数是4．
故答案为：0.4，4．
12．解：由题意可知第n个单项式是（﹣1）n﹣12n﹣1xn，即（﹣2）n﹣1xn，第7个单项式为（﹣1）7﹣127﹣1x7，即64x7．
故答案为：64x7；（﹣2）n﹣1xn．
13．解：（1+2）（1+22）（1+24）（1+28）…（1+2n），
=（2﹣1）（1+2）（1+22）（1+24）（1+28）…（1+2n），
=（22﹣1）（1+22）（1+24）（1+28）…（1+2n），
=（2n﹣1）（1+2n），
=22n﹣1，
∴x+1=22n﹣1+1=22n，
2n=128，
∴n=64．
故填64．
14．解：∵多项式（m﹣2）x2﹣mx+3中的x的一次项系数为﹣2，∴﹣m=﹣2，m=2，
把m=2代入多项式（m﹣2）x2﹣mx+3中，m﹣2=0，∴二次项系数为0，多项式为一次二项式．
15．解：由同类项的定义可知x=2，
2m=n﹣1，即2m﹣n=﹣1，
所以（2m﹣n）x=（﹣1）2=1．
16．解：∵单项式﹣xm﹣2y3与xny2m﹣3n的和仍是单项式，
∴m﹣2=n，2m﹣3n=3，
解得：m=3，n=1，
∴m﹣n=3﹣1=；
故答案为：．
17．解：如图所示，将四块草坪平移到一块儿整体计算；
草坪的面积S=（a﹣x）（b﹣x）=ab﹣（a+b）x+x2．
18．解：3（8y﹣x）﹣5（x+6y﹣2）=24y﹣3x﹣5x﹣30y+10=﹣8x﹣6y+10=﹣2（4x+3y）+10=﹣2×（﹣5）+10=20．
19．解：如图，当圆环为3个时，链长为3a+×2=2a+b（cm），
∴当圆环为50个时，链长为50a+2×=49a+b（cm），故答案为（49a+b）．
20．解：通过找规律可知，每项的结果为等式左边项数的平方，即n2，而1+3+5+7…+99共有50项，所以结果是502=2500．
三．解答题（共6小题，满分40分）
21．解：M﹣2N=（3x2+2x﹣1）﹣2（﹣x2﹣2+3x）
=3x2+2x﹣1+2x2+4﹣6x
=5x2﹣4x+3．
22．解：∵（2x2+ax﹣y+b）﹣（2bx2﹣3x+5y﹣1）=（2﹣2b）x2+（a+3）x﹣6y+b+1，
又∵（2x2+ax﹣y+b）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，
∴2﹣2b=0，a+3=0，
∴a=﹣3，b=1．
23．解：原式=2a2b+2ab2﹣2a2b+2﹣ab2﹣2
=ab2，
当a=1，b=﹣3时，原式=1×（﹣3）2=9．
24．解：原式=2a2b+2ab2﹣2a2b+2﹣ab2﹣2
=ab2，
当a=2，b=﹣1时，原式=2×（﹣1）2=2．
25．解：（1）根据题意得：
甲车开出7小时时的位置为：190﹣7×（200÷5）=﹣90（km），
流动加油车出发位置为：270﹣（270﹣170）÷2×7=﹣80（km）；
故答案为：﹣90，﹣80；
（2）根据题意得：
当两车同时开出x小时时，甲车位置为：190﹣40x，
流动加油车位置为：﹣80+50x；
（3）当x=3时，甲车开出的位置是：190﹣40x=70（km），
流动加油车的位置是：﹣80+50x=70（km），
则甲车能立刻获得流动加油车的帮助．
26．解：（1）∵图1中有1盆花，
图2中有1+6=7盆花，
图3中有1+6+6×2=19盆花，
…
∴第n个图中有1+6×（1+2+3+…+n﹣1）=3n（n﹣1）+1盆花；
∴图4中，应该有12×（4﹣1）+1=37盆花，图5中，应该有15×（5﹣1）+1=61盆花；
（2）第n个图形中花盆的盆数为3n（n﹣1）+1．
故答案为：37，61；3n（n﹣1）+1．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)