1.5 全等三角形的判定(3)(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 1.5 全等三角形的判定(3)(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | doc | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-10 18:08:47 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
浙江版八年级数学上册第一章1.5全等三角形的判定
第3课时 三角形全等的判定(3)
【知识清单】
1. 全等三角形判定3: 两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);
2.注意书写格式:角边角中的边是指两对应角的夹边,在证明过程中边一定要放在两组对应角的中间.
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
3.灵活运用三角形全等判定(SSS、SAS、ASA):在证明两个三角形全等时要灵活运用所给的条件,选择不同的判断方法,尤其一个题目需要多次全等才能完成的,所以在证明过程中一定要保持清醒的头脑,清晰的思路,规范的书写格式.
4.考点:证明三角形全等,以及在三角形全等的基础之上进一步证明线段、角度之间的数量关系.
【经典例题】
例题1,下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【解答】解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
图丙的三角形中第三个角为61°,与△ABC满足三角形全等的判定方法:ASA,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选:B.
【点评】本题考查了三角形全等的判定方法,属于最基本题型.
例题2,如图,BE是∠MBN的平分线,点A是BN上的任意一点,过点A作AE⊥BE于点E,过A作AC⊥BM于C,AC与BE相交于点H,若AC=BC,试猜想AE与BH的数量关系,并说明理由.
【答案】:BH=2AE. 理由如下:
【分析】:要想得出AE与BH的关系,根据现有的知识只能用三角形全等来解决,而图中没有全等三角形可以利用,因此需要添加辅助线构造全等三角形.延长AE交BM于点G.便可得出△HBC≌△GAC(ASA),得到AG=BH;再由BE平分∠MBN,可得∠ABE=∠GBE;由AE⊥BE,可得∠AEB=∠GEB=90°,从而推出△BAE≌△BGE(ASA),得出AG=2AE,所以BH=2AE.
【详解】:延长AE交BM于点G.
∵AC⊥BM(已知),
∴∠HCB=∠GCA=90°(垂直定义)
∵∠HBC+∠BHC=90°,∠AHE+∠EAH=90°(直角三角形两锐角互余)
∵∠BHC=∠AHE(对顶角相等).
∴∠HBC=∠EAH(等量代换)
在△HBC和△GAC中,
∴△HBC≌△GAC(ASA).
∴BH=AG(全等三角形对应边相等).
∵AE⊥BE(已知),
∴∠BEA=∠BEG=90°.
在△BAE和△BGE中,
∴△BAE≌△BGE(ASA).
∴AE=EG(全等三角形对应边相等).
∴
【点评】:主要考查三角形全等的判定,寻找三角形全等的条件是解决问题的关键.
【夯实基础】
1.如图,∠1=∠2, ∠3=∠4,下列结论错误的是( )
A. △ABC≌△DCB B. △AOB≌△DOC C. △ABD≌△DCA D. △AOD≌△BOC
2. 如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,所示某人将一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.④
4.如图∠1=∠2=∠3,AB=AD,AE=5,则AC的长度为 .
5.如图FB∥DE,AE=CF,要使△ABF≌△CDE,,(1)若以“SAS”为依据,需添加的条件
是______;(2)若以“ASA”为依据,需添加的条件是______.
6.如图,△ABC的两条高AD , BE相交于点F , 请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是________.
7.如图,在△ABC中,∠BAC=90°,AB=AC,BD是AC边上的中线,过点A作AE⊥BD于H,过点C作EC⊥AC,交AE于E,求证:
【提优特训】
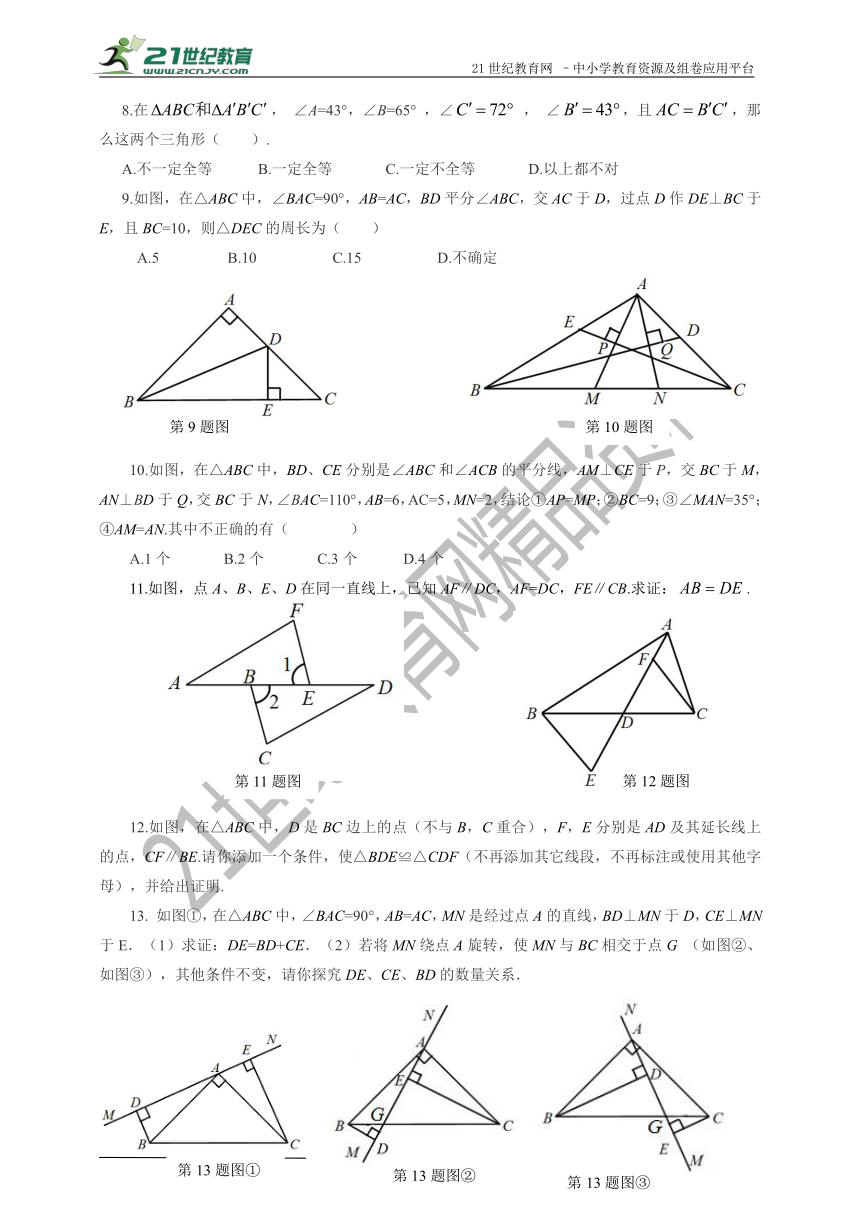
8.在, ∠A=43°,∠B=65° ,∠ , ∠,且,那么这两个三角形( ).
A.不一定全等 B.一定全等 C.一定不全等 D.以上都不对
9.如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,过点D作DE⊥BC于E,且BC=10,则△DEC的周长为( )
A.5 B.10 C.15 D.不确定
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,点A、B、E、D在同一直线上,已知AF∥DC,AF=DC,FE∥CB.求证:.
12.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF(不再添加其它线段,不再标注或使用其他字母),并给出证明.
13. 如图①,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E.(1)求证:DE=BD+CE.(2)若将MN绕点A旋转,使MN与BC相交于点G (如图②、如图③),其他条件不变,请你探究DE、CE、BD的数量关系.
【中考链接】
14.2018年四川乐山19.如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.
15.2018广西柳州(6.00分)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
16.2018莆田19.在△ABC中,D是AB的中点,E是CD的中点.过的C作CF∥AB交AE的延长线于点F,连接BF.求证:DB=CF.
17.2018年湖南省怀化19.(10.00分)已知:如图,点A、F、E、C在同一直线上,AB∥DC,AB=CD,∠B=∠D.求证:△ABE≌△CDF;
参考答案
1.D 2.C 3.D 4.AC=5 5.(1)FB=ED,(2)∠A=∠C. 6.DC=EC或AC=BC或AD=BC.
8.B 9.B 10.C
7.证明:∵∠BAC=90°(已知),
∴∠BAH+∠EAC=90°(直角定义),
∵AE⊥BD(已知),
∴∠AHB=90°(垂直定义),
∴∠ABH+∠BAH=90°(直角三角形两锐角互余).
∴∠ABH=∠CAE(等量代换)
∵EC⊥AC(已知)
∴∠ACE=90°(垂直定义)
∴∠BAC=∠ACE(等量代换)
在△ABD和△CAE,
∴△ABD≌△CAE(ASA),
∴AD=CE(全等三角形对应边相等).
∵D为AC的中点(已知),
∴(中点定义).
∴(等量代换).
11.证明:∵AF∥DC(已知),
∴ ∠A=∠D(两直线平行内错角相等).
∵FE∥CB(已知),
∴∠1=∠2(两直线平行内错角相等)
∵∠F=180-(∠A+∠1),∠C=180-(∠D+∠2)(三角形内角和定理)
∴∠F=∠C(等量代换)
在△AFE和△DCB中,
∴△AFE≌△DCB(ASA)
∴AE=DB(全等三角形对应边相等).
∴AE-BE=DB-EB(等量减等量差相等).
即AB=DE.
12.解:(1)你添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
13.证明:如图①,(1)∵BD⊥MN,CE⊥MN(已知),
∴∠BDA=∠AEC=90°(直角定义)
∴∠DBA+∠DAB=90°,∠CAE+∠ECA=90°(直角三角形两锐角互余).
∵∠BAC=90°(已知),
∴∠DAB+∠CAE=90°(平角定义).
∴∠DBA=∠EAC,∠DAB=∠ECA(等式性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(ASA),
∴BD=AE,AD=CE(全等三角形对应边相等),
DE=AD+AE=BD+CE(等量代换).
解答:(2)如图②∵BD⊥MN,CE⊥MN(已知),
∴∠BDA=∠AEC=90°(直角定义)
∴∠DBA+∠DAB=90°,∠CAE+∠ECA=90°(直角三角形两锐角互余).
∵∠BAC=90°(已知),
∴∠DAB+∠CAE=90°.
∴∠DBA=∠EAC,∠DAB=∠ECA(等式性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(ASA),
∴BD=AE,AD=CE(全等三角形对应边相等),
∴DE=AD-AE= CE -BD(等量代换).
(2)如图③的证明过程与(2)如图②相同,
DE= AE-AD = BD -CE(等量代换).
14.【分析】根据ASA证明△ADB≌△ACB,可得结论.
【解答】证明:∵∠ABD+∠3=180°∠ABC+∠4=180°,且∠3=∠4,
∴∠ABD=∠ABC
在△ADB和△ACB中,
∴△ADB≌△ACB(ASA),
∴BD=CD.
【点评】本题考查了三角形外角的性质、三角形全等的性质和判定,熟练掌握三角形全等的判定是关键.
15.【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.
【解答】证明:∵在△ABC和△EDC中,
∴△ABC≌△EDC(ASA).
【点评】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.
16.【考点】全等三角形的判定与性质、平行线的性质.
【专题】三角形
【分析】根据E为CD的中点,得CE=DE,∠AED和∠CEF
是对顶角,CF∥AB,可得∠EDA=∠ECF,利用ASA
证明△ADE≌△FCE,可得AD=FC,因为D为AB的中点,
可得AD=BD即可得出结论.
【解答】证明:∵E为CD的中点,∴CE=DE,
∵∠AED和∠CEF是对顶角,∴∠AED=∠CEF.
∵CF∥AB,
∴∠EDA=∠ECF.
在△EDA和△ECF中,
∴AD=FC
∵D为AB的中点,
∴AD=BD.∴DB=CF.
【点评】本题考查了平行四边形的判定和性质、全等三角形的判定和性质,属于简单题型.
17.【分析】(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;
(2)利用全等三角形的性质和中点的性质解答即可.
【解答】证明:(1)∵AB∥DC,∴∠A=∠C,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA).
例题1图
例题2图
例题2图
第2题图
第1题图
第4题图
第3题图
第6题图
第5题图
第7题图
第10题图
第9题图
第11题图
第12题图
第13题图③
第13题图②
第13题图①
第15题图
第14题图
第16题图
第17题图
第7题图
第11题图
第12题图
第13题图①
第13题图②
第13题图③
第14题图
第15题图
第16题图
第17题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江版八年级数学上册第一章1.5全等三角形的判定
第3课时 三角形全等的判定(3)
【知识清单】
1. 全等三角形判定3: 两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);
2.注意书写格式:角边角中的边是指两对应角的夹边,在证明过程中边一定要放在两组对应角的中间.
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
3.灵活运用三角形全等判定(SSS、SAS、ASA):在证明两个三角形全等时要灵活运用所给的条件,选择不同的判断方法,尤其一个题目需要多次全等才能完成的,所以在证明过程中一定要保持清醒的头脑,清晰的思路,规范的书写格式.
4.考点:证明三角形全等,以及在三角形全等的基础之上进一步证明线段、角度之间的数量关系.
【经典例题】
例题1,下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【解答】解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
图丙的三角形中第三个角为61°,与△ABC满足三角形全等的判定方法:ASA,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选:B.
【点评】本题考查了三角形全等的判定方法,属于最基本题型.
例题2,如图,BE是∠MBN的平分线,点A是BN上的任意一点,过点A作AE⊥BE于点E,过A作AC⊥BM于C,AC与BE相交于点H,若AC=BC,试猜想AE与BH的数量关系,并说明理由.
【答案】:BH=2AE. 理由如下:
【分析】:要想得出AE与BH的关系,根据现有的知识只能用三角形全等来解决,而图中没有全等三角形可以利用,因此需要添加辅助线构造全等三角形.延长AE交BM于点G.便可得出△HBC≌△GAC(ASA),得到AG=BH;再由BE平分∠MBN,可得∠ABE=∠GBE;由AE⊥BE,可得∠AEB=∠GEB=90°,从而推出△BAE≌△BGE(ASA),得出AG=2AE,所以BH=2AE.
【详解】:延长AE交BM于点G.
∵AC⊥BM(已知),
∴∠HCB=∠GCA=90°(垂直定义)
∵∠HBC+∠BHC=90°,∠AHE+∠EAH=90°(直角三角形两锐角互余)
∵∠BHC=∠AHE(对顶角相等).
∴∠HBC=∠EAH(等量代换)
在△HBC和△GAC中,
∴△HBC≌△GAC(ASA).
∴BH=AG(全等三角形对应边相等).
∵AE⊥BE(已知),
∴∠BEA=∠BEG=90°.
在△BAE和△BGE中,
∴△BAE≌△BGE(ASA).
∴AE=EG(全等三角形对应边相等).
∴
【点评】:主要考查三角形全等的判定,寻找三角形全等的条件是解决问题的关键.
【夯实基础】
1.如图,∠1=∠2, ∠3=∠4,下列结论错误的是( )
A. △ABC≌△DCB B. △AOB≌△DOC C. △ABD≌△DCA D. △AOD≌△BOC
2. 如图,AE=AD,∠1=∠2,∠E=∠D,结论①BF=CG;②OF=OG;③EF=DG;④AG=GC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,所示某人将一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.④
4.如图∠1=∠2=∠3,AB=AD,AE=5,则AC的长度为 .
5.如图FB∥DE,AE=CF,要使△ABF≌△CDE,,(1)若以“SAS”为依据,需添加的条件
是______;(2)若以“ASA”为依据,需添加的条件是______.
6.如图,△ABC的两条高AD , BE相交于点F , 请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是________.
7.如图,在△ABC中,∠BAC=90°,AB=AC,BD是AC边上的中线,过点A作AE⊥BD于H,过点C作EC⊥AC,交AE于E,求证:
【提优特训】
8.在, ∠A=43°,∠B=65° ,∠ , ∠,且,那么这两个三角形( ).
A.不一定全等 B.一定全等 C.一定不全等 D.以上都不对
9.如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,过点D作DE⊥BC于E,且BC=10,则△DEC的周长为( )
A.5 B.10 C.15 D.不确定
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,点A、B、E、D在同一直线上,已知AF∥DC,AF=DC,FE∥CB.求证:.
12.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF(不再添加其它线段,不再标注或使用其他字母),并给出证明.
13. 如图①,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E.(1)求证:DE=BD+CE.(2)若将MN绕点A旋转,使MN与BC相交于点G (如图②、如图③),其他条件不变,请你探究DE、CE、BD的数量关系.
【中考链接】
14.2018年四川乐山19.如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.
15.2018广西柳州(6.00分)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
16.2018莆田19.在△ABC中,D是AB的中点,E是CD的中点.过的C作CF∥AB交AE的延长线于点F,连接BF.求证:DB=CF.
17.2018年湖南省怀化19.(10.00分)已知:如图,点A、F、E、C在同一直线上,AB∥DC,AB=CD,∠B=∠D.求证:△ABE≌△CDF;
参考答案
1.D 2.C 3.D 4.AC=5 5.(1)FB=ED,(2)∠A=∠C. 6.DC=EC或AC=BC或AD=BC.
8.B 9.B 10.C
7.证明:∵∠BAC=90°(已知),
∴∠BAH+∠EAC=90°(直角定义),
∵AE⊥BD(已知),
∴∠AHB=90°(垂直定义),
∴∠ABH+∠BAH=90°(直角三角形两锐角互余).
∴∠ABH=∠CAE(等量代换)
∵EC⊥AC(已知)
∴∠ACE=90°(垂直定义)
∴∠BAC=∠ACE(等量代换)
在△ABD和△CAE,
∴△ABD≌△CAE(ASA),
∴AD=CE(全等三角形对应边相等).
∵D为AC的中点(已知),
∴(中点定义).
∴(等量代换).
11.证明:∵AF∥DC(已知),
∴ ∠A=∠D(两直线平行内错角相等).
∵FE∥CB(已知),
∴∠1=∠2(两直线平行内错角相等)
∵∠F=180-(∠A+∠1),∠C=180-(∠D+∠2)(三角形内角和定理)
∴∠F=∠C(等量代换)
在△AFE和△DCB中,
∴△AFE≌△DCB(ASA)
∴AE=DB(全等三角形对应边相等).
∴AE-BE=DB-EB(等量减等量差相等).
即AB=DE.
12.解:(1)你添加的条件是: BD=CD ;
(2)证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行内错角相等),
在△BDE和△CDF中,
∴△BDE≌△CDF(ASA)
13.证明:如图①,(1)∵BD⊥MN,CE⊥MN(已知),
∴∠BDA=∠AEC=90°(直角定义)
∴∠DBA+∠DAB=90°,∠CAE+∠ECA=90°(直角三角形两锐角互余).
∵∠BAC=90°(已知),
∴∠DAB+∠CAE=90°(平角定义).
∴∠DBA=∠EAC,∠DAB=∠ECA(等式性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(ASA),
∴BD=AE,AD=CE(全等三角形对应边相等),
DE=AD+AE=BD+CE(等量代换).
解答:(2)如图②∵BD⊥MN,CE⊥MN(已知),
∴∠BDA=∠AEC=90°(直角定义)
∴∠DBA+∠DAB=90°,∠CAE+∠ECA=90°(直角三角形两锐角互余).
∵∠BAC=90°(已知),
∴∠DAB+∠CAE=90°.
∴∠DBA=∠EAC,∠DAB=∠ECA(等式性质).
在△ADB和△CEA中,
∴△ADB≌△CEA(ASA),
∴BD=AE,AD=CE(全等三角形对应边相等),
∴DE=AD-AE= CE -BD(等量代换).
(2)如图③的证明过程与(2)如图②相同,
DE= AE-AD = BD -CE(等量代换).
14.【分析】根据ASA证明△ADB≌△ACB,可得结论.
【解答】证明:∵∠ABD+∠3=180°∠ABC+∠4=180°,且∠3=∠4,
∴∠ABD=∠ABC
在△ADB和△ACB中,
∴△ADB≌△ACB(ASA),
∴BD=CD.
【点评】本题考查了三角形外角的性质、三角形全等的性质和判定,熟练掌握三角形全等的判定是关键.
15.【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.
【解答】证明:∵在△ABC和△EDC中,
∴△ABC≌△EDC(ASA).
【点评】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.
16.【考点】全等三角形的判定与性质、平行线的性质.
【专题】三角形
【分析】根据E为CD的中点,得CE=DE,∠AED和∠CEF
是对顶角,CF∥AB,可得∠EDA=∠ECF,利用ASA
证明△ADE≌△FCE,可得AD=FC,因为D为AB的中点,
可得AD=BD即可得出结论.
【解答】证明:∵E为CD的中点,∴CE=DE,
∵∠AED和∠CEF是对顶角,∴∠AED=∠CEF.
∵CF∥AB,
∴∠EDA=∠ECF.
在△EDA和△ECF中,
∴AD=FC
∵D为AB的中点,
∴AD=BD.∴DB=CF.
【点评】本题考查了平行四边形的判定和性质、全等三角形的判定和性质,属于简单题型.
17.【分析】(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;
(2)利用全等三角形的性质和中点的性质解答即可.
【解答】证明:(1)∵AB∥DC,∴∠A=∠C,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA).
例题1图
例题2图
例题2图
第2题图
第1题图
第4题图
第3题图
第6题图
第5题图
第7题图
第10题图
第9题图
第11题图
第12题图
第13题图③
第13题图②
第13题图①
第15题图
第14题图
第16题图
第17题图
第7题图
第11题图
第12题图
第13题图①
第13题图②
第13题图③
第14题图
第15题图
第16题图
第17题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
