2.3 等腰三角形的性质定理 第1课时(知识清单+经典例题+夯实基础+提优训练+中考链接)
文档属性
| 名称 | 2.3 等腰三角形的性质定理 第1课时(知识清单+经典例题+夯实基础+提优训练+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-25 16:40:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江版八年级数学上册第2章特殊三角形2.3等腰三角形的性质定理
第1课时 等腰三角形的性质定理(1)
【知识清单】
1.等腰三角形的性质:
等腰三角形的两底角相等(即在同一个三角形中,等边对等角).
如图1,几何语言:在△ABC中,
∵AB=AC,
∴∠B=∠C.
2.推论:
等边三角形的各内角都等于60°.
3.轴对称性:
等腰三角形是轴对称图形,它的对称轴有1条或3条.
4.考点:等腰三角形的性质定理以及与之的边、角计算.
【经典例题】
例题1 ,如图,在△ABC中,
(1)用尺规作图方法作出BC边上的中线;
(2)若,试问∠BAC的度数?说明理由.
【分析】由尺规作图求出BC的中点,连接AD即为BC边上的中线,利用等腰三角形的性质定理可得两个角相等,∠B=∠1,∠2=∠C,再由三角形的内角和定理问题得到解决.
【解答】(1)如图,作法:①作线段BC的垂直平分线MN,交BC于D,则点D为BC的中点,
②连接AD,AD就是所求的中线.
(2)∠BAC=90°,理由如下:
∵AD是BC边的中线(由作图可知),
∴点D为中点(中线定义),
∴(中线定义).
∵(已知),
∴AD=BD=CD(等量代换),
∴∠B=∠1,∠2=∠C(等边对等角),
∴∠B+∠1+∠2+∠C=180°(三角形内角和定理),
∴2(∠1+∠2)=180°(等量代换),
∴∠1+∠2=90°.
∴∠BAC=90°.
【点评】此题考查了尺规作图和等腰三角形的性质定理,熟练掌握等腰三角形的性质定理和三角形内角和定理是解决问题的关键.
例题2,已知等腰三角形两角的差为30°,求等腰三角形顶角的度数.
【分析】等腰三角形两底角相等,两角的差为30°,即顶角与底角的差为30°或底角与顶角的差为30°.分组讨论做到不遗不漏.
【解答】设等腰三角形的顶角为x°,底角为y°,
根据题意,得和
解方程组,得和
所以等腰三角形的顶角为80°或40°.
【点评】此题考查等腰三角形定义和性质定理,分组讨论和三角形内角和定理是解决问题的关键.
【夯实基础】
1、在△ABC中,AB=AC,∠A=50°则∠C的度数为( )
A.50° B.65° C.50°或65° D.67.5°
2、如图,△ABC是等腰三角形,AC=BC,△BCD是等边三角形,则∠A的度数为( )
A.30° B. 45° C. 50° D. 55°
3、如图,BD是△ABC的角平分线,交AC于D,BC的中垂线,交BC于F,交BD于E,连接EC,若∠A=85°,∠1=20°,则∠4的度数为( )
A.25° B.35° C. 45° D.55°
4、如图,点D是△ABC内一点,AD=BD=CD,若∠BAC=50°则∠DBC度数是( )
A. 55° B.50° C.45° D. 40°
5、已知等腰三角形的一个内角为75°,则另两个角的度数是 .
6、等腰三角形的一个内角与顶角的外角之和为132°,则这个等腰三角形的顶角等于 ,底角等于 .
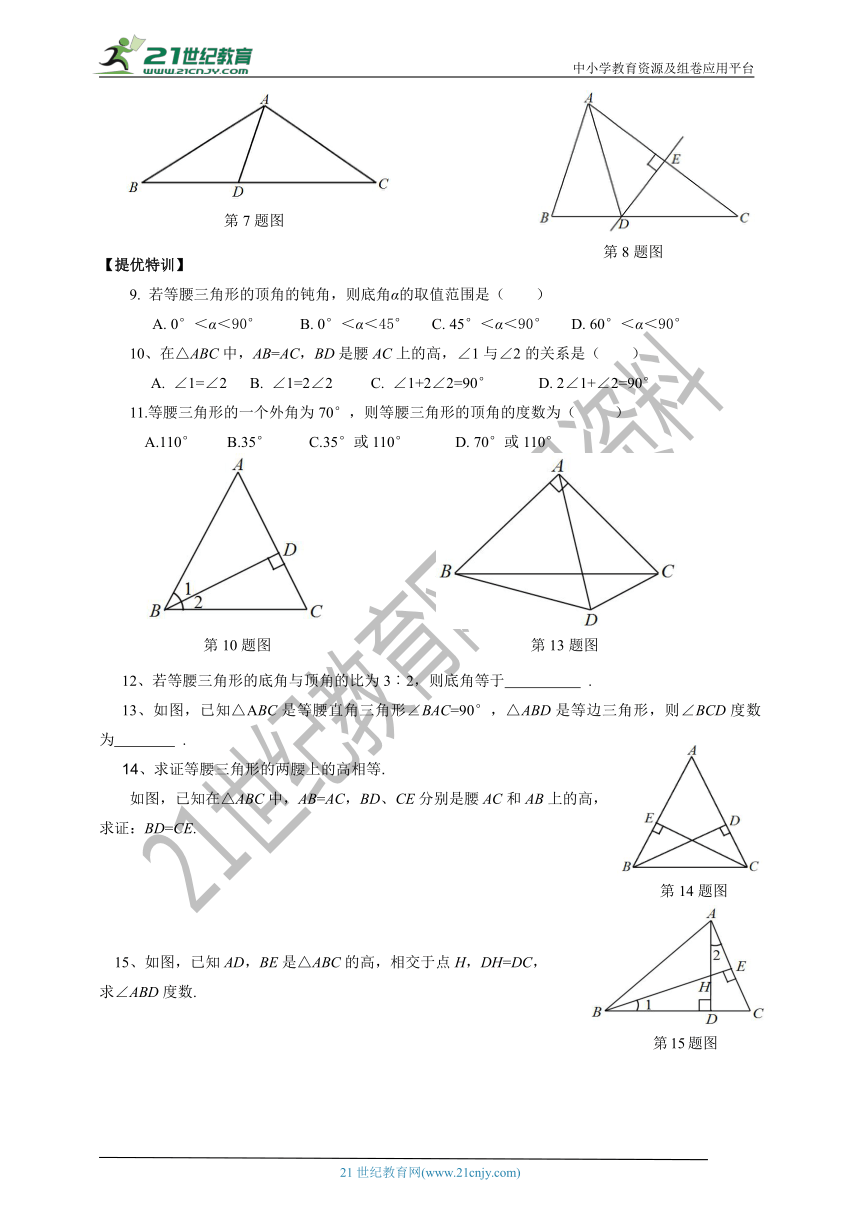
7、如图,在△ABC中,AB=AC=CD, AD=BD,则∠BAC的度数为 .
8、如图,在△ABC中,AB=AD,∠BAD=28°,直线DE垂直平分AC,求∠B和∠C的度数.
【提优特训】
9. 若等腰三角形的顶角的钝角,则底角α的取值范围是( )
A. 0°<α<90° B. 0°<α<45° C. 45°<α<90° D. 60°<α<90°
10、在△ABC中,AB=AC,BD是腰AC上的高,∠1与∠2的关系是( )
A. ∠1=∠2 B. ∠1=2∠2 C. ∠1+2∠2=90° D. 2∠1+∠2=90°
11.等腰三角形的一个外角为70°,则等腰三角形的顶角的度数为( )
A.110° B.35° C.35°或110° D. 70°或110°
12、若等腰三角形的底角与顶角的比为3︰2,则底角等于 .
13、如图,已知△ABC是等腰直角三角形∠BAC=90°,△ABD是等边三角形,则∠BCD度数为 .
14、求证等腰三角形的两腰上的高相等.
如图,已知在△ABC中,AB=AC,BD、CE分别是腰AC和AB上的高,
求证:BD=CE.
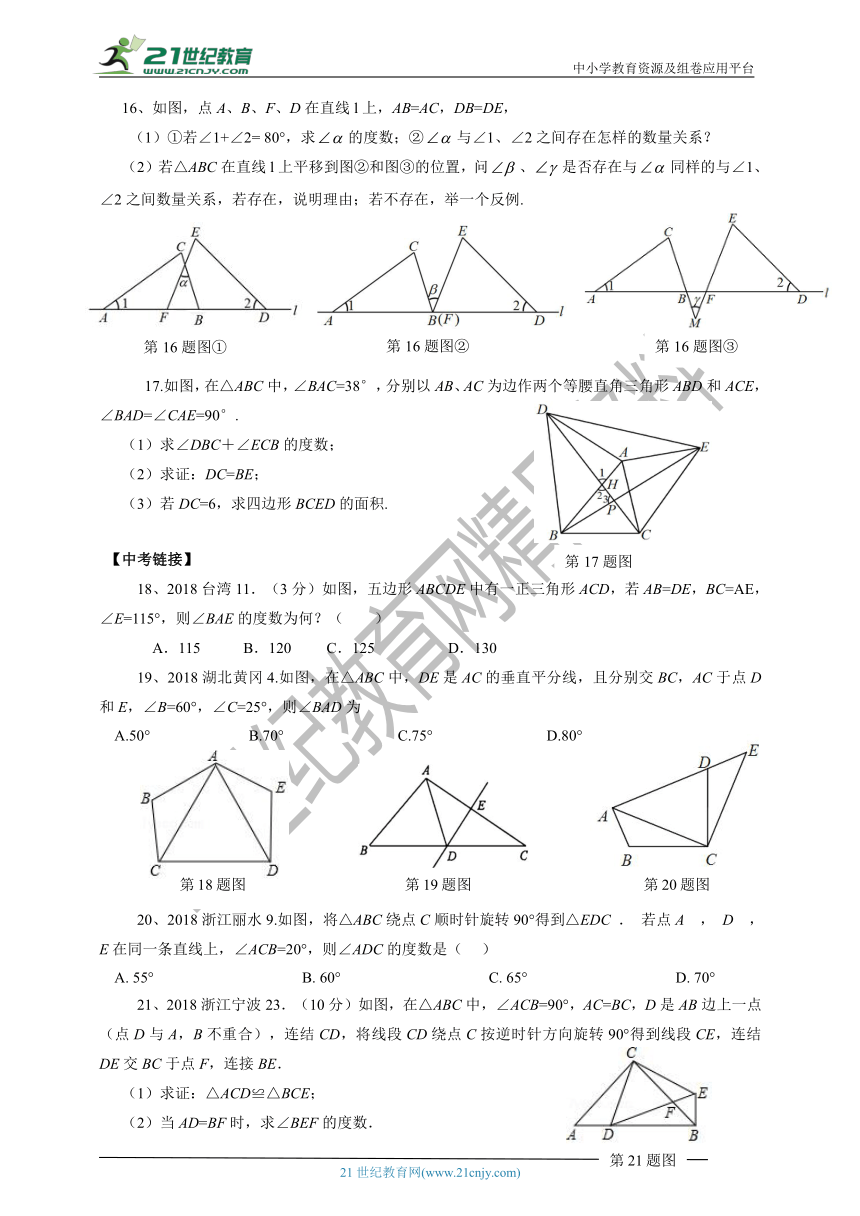
15、如图,已知AD,BE是△ABC的高,相交于点H,DH=DC,
求∠ABD度数.
16、如图,点A、B、F、D在直线l上,AB=AC,DB=DE,
(1)①若∠1+∠2= 80°,求的度数;②与∠1、∠2之间存在怎样的数量关系?
(2)若△ABC在直线l上平移到图②和图③的位置,问、是否存在与同样的与∠1、∠2之间数量关系,若存在,说明理由;若不存在,举一个反例.
17.如图,在△ABC中,∠BAC=38°,分别以AB、AC为边作两个等腰直角三角形ABD和ACE,∠BAD=∠CAE=90°.
(1)求∠DBC+∠ECB的度数;
(2)求证:DC=BE;
(3)若DC=6,求四边形BCED的面积.
【中考链接】
18、2018台湾11.(3分)如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )
A.115 B.120 C.125 D.130
19、2018湖北黄冈4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为
A.50° B.70° C.75° D.80°
20、2018浙江丽水9.如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A. 55° B. 60° C. 65° D. 70°
21、2018浙江宁波23.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
参考答案
1、B 2、A 3、B 4、D 5、52.5°,52.5°或75°,30° 6、92°,44° 7、108°
9、B 10、C 11、A 12、67.5° 13、30 18、C 19、B 20、C.
8、解:∵AB=AD(已知),
∴∠B=∠ADB=(三角形内角和定理).
∵DE垂直平分AC(已知),
∴DA=DC(线段平分线上的到线段两个端点的距离相等).
∴∠C=∠DAC(等边对等角).
∵∠ADB=∠C+∠DAC(三角形的一个外角等于和
它不相邻两个内角的和)
∴∠C=∠DAC=
14、证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是腰AC和AB上的高,
∴∠BEC=∠CDB=90°(垂直定义).
在△BEC和△CDB中,
∵
∴△BEC≌△CDB(AAS)
∴CE=BD(全等三角形对应边相等).
15、解:∵AD,BE是△ABC的高,
∴∠ADB=∠ADC=∠BEC=90°(垂直定义)
∴∠1+∠C=90°,∠2+∠C=90°(直角三角形两个锐角互余)
∴∠1=∠2
在△BHD和△ACD中,
∵
∴△BHD≌△ACD(AAS)
∴BD=AD(全等三角形对应边相等).
∴∠ABD=∠DAB(等边对等角).
∵∠ABD+∠DAB=90°(直角三角形两锐角互余),
∴∠ABD=∠DAB =45°.
16、解:(1)①∵AF=AC,DB=DE,
∴△ABC和△DEF都是等腰三角形,
∴
,
同理
∵
∴
②由①可知
(2)、与存在同样的与∠1、∠2之间数量关系.
即
理由:所求的、、均与两个等腰三角形的两个底角之和为180°.
17、解答:(1)∵△ABD和△ACE均为等腰直角三角形,且∠BAD=∠CAE=90°,
∴∠ ABD=∠ACE=45°
∵∠BAC=38°,
∴∠ABC+∠ACB=180°-∠BAC =180°-38°=142°.
∴∠DBC+∠ECB=∠ABD+∠ABC+∠ACB+∠ACE
=45°+142°+45°=232°.
(2)∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC =∠CAE+∠BAC
即∠DAC=∠BAE.
在△DAC和△BAE中,
∵
∴△DAC≌△BAE(SAS).
∴DC=BE(全等三角形对应边相等).
(3)由(2)知△DAC≌△BAE,
∴∠ADC=∠ABE
∵∠1=∠2(对顶角相等)
∴∠3=∠BAD=90°.
∴DC⊥BE
∵DC=6,
∴BE =DC=6.
∴四边形BCED的面积=
21、【分析】(1)由题意可知:CD=CE,∠DCE=90°,由于∠ACB=90°,所以∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,所以∠ACD=∠BCE,从而可证明△ACD≌△BCE(SAS)
(2)由△ACD≌△BCE(SAS)可知:∠A=∠CBE=45°,BE=BF,从而可求出∠BEF的度数.
【解答】解:(1)由题意可知:CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB,
∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
∵
∴△ACD≌△BCE(SAS)
(2)∵∠ACB=90°,AC=BC,
∴∠A=45°,
由(1)可知:∠A=∠CBE=45°,
∵AD=BF,
∴BE=BF,
∴∠BEF=67.5°
【点评】本题考查全等三角形的判定与性质,解题的关键是熟练运用旋转的性质以及全等三角形的判定与性质,本题属于中等题型.
图1
例题1图
例题1图
第3题图
第4题图
第2题图
第7题图
第8题图
第13题图
第10题图
第14题图
第15题图
第16题图③
第16题图①
第16题图②
第17题图
第18题图
第20题图
第19题图
第21题图
第8题图
第14题图
第15题图
第16题图①
第16题图③
第16题图②
第17题图
第21题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江版八年级数学上册第2章特殊三角形2.3等腰三角形的性质定理
第1课时 等腰三角形的性质定理(1)
【知识清单】
1.等腰三角形的性质:
等腰三角形的两底角相等(即在同一个三角形中,等边对等角).
如图1,几何语言:在△ABC中,
∵AB=AC,
∴∠B=∠C.
2.推论:
等边三角形的各内角都等于60°.
3.轴对称性:
等腰三角形是轴对称图形,它的对称轴有1条或3条.
4.考点:等腰三角形的性质定理以及与之的边、角计算.
【经典例题】
例题1 ,如图,在△ABC中,
(1)用尺规作图方法作出BC边上的中线;
(2)若,试问∠BAC的度数?说明理由.
【分析】由尺规作图求出BC的中点,连接AD即为BC边上的中线,利用等腰三角形的性质定理可得两个角相等,∠B=∠1,∠2=∠C,再由三角形的内角和定理问题得到解决.
【解答】(1)如图,作法:①作线段BC的垂直平分线MN,交BC于D,则点D为BC的中点,
②连接AD,AD就是所求的中线.
(2)∠BAC=90°,理由如下:
∵AD是BC边的中线(由作图可知),
∴点D为中点(中线定义),
∴(中线定义).
∵(已知),
∴AD=BD=CD(等量代换),
∴∠B=∠1,∠2=∠C(等边对等角),
∴∠B+∠1+∠2+∠C=180°(三角形内角和定理),
∴2(∠1+∠2)=180°(等量代换),
∴∠1+∠2=90°.
∴∠BAC=90°.
【点评】此题考查了尺规作图和等腰三角形的性质定理,熟练掌握等腰三角形的性质定理和三角形内角和定理是解决问题的关键.
例题2,已知等腰三角形两角的差为30°,求等腰三角形顶角的度数.
【分析】等腰三角形两底角相等,两角的差为30°,即顶角与底角的差为30°或底角与顶角的差为30°.分组讨论做到不遗不漏.
【解答】设等腰三角形的顶角为x°,底角为y°,
根据题意,得和
解方程组,得和
所以等腰三角形的顶角为80°或40°.
【点评】此题考查等腰三角形定义和性质定理,分组讨论和三角形内角和定理是解决问题的关键.
【夯实基础】
1、在△ABC中,AB=AC,∠A=50°则∠C的度数为( )
A.50° B.65° C.50°或65° D.67.5°
2、如图,△ABC是等腰三角形,AC=BC,△BCD是等边三角形,则∠A的度数为( )
A.30° B. 45° C. 50° D. 55°
3、如图,BD是△ABC的角平分线,交AC于D,BC的中垂线,交BC于F,交BD于E,连接EC,若∠A=85°,∠1=20°,则∠4的度数为( )
A.25° B.35° C. 45° D.55°
4、如图,点D是△ABC内一点,AD=BD=CD,若∠BAC=50°则∠DBC度数是( )
A. 55° B.50° C.45° D. 40°
5、已知等腰三角形的一个内角为75°,则另两个角的度数是 .
6、等腰三角形的一个内角与顶角的外角之和为132°,则这个等腰三角形的顶角等于 ,底角等于 .
7、如图,在△ABC中,AB=AC=CD, AD=BD,则∠BAC的度数为 .
8、如图,在△ABC中,AB=AD,∠BAD=28°,直线DE垂直平分AC,求∠B和∠C的度数.
【提优特训】
9. 若等腰三角形的顶角的钝角,则底角α的取值范围是( )
A. 0°<α<90° B. 0°<α<45° C. 45°<α<90° D. 60°<α<90°
10、在△ABC中,AB=AC,BD是腰AC上的高,∠1与∠2的关系是( )
A. ∠1=∠2 B. ∠1=2∠2 C. ∠1+2∠2=90° D. 2∠1+∠2=90°
11.等腰三角形的一个外角为70°,则等腰三角形的顶角的度数为( )
A.110° B.35° C.35°或110° D. 70°或110°
12、若等腰三角形的底角与顶角的比为3︰2,则底角等于 .
13、如图,已知△ABC是等腰直角三角形∠BAC=90°,△ABD是等边三角形,则∠BCD度数为 .
14、求证等腰三角形的两腰上的高相等.
如图,已知在△ABC中,AB=AC,BD、CE分别是腰AC和AB上的高,
求证:BD=CE.
15、如图,已知AD,BE是△ABC的高,相交于点H,DH=DC,
求∠ABD度数.
16、如图,点A、B、F、D在直线l上,AB=AC,DB=DE,
(1)①若∠1+∠2= 80°,求的度数;②与∠1、∠2之间存在怎样的数量关系?
(2)若△ABC在直线l上平移到图②和图③的位置,问、是否存在与同样的与∠1、∠2之间数量关系,若存在,说明理由;若不存在,举一个反例.
17.如图,在△ABC中,∠BAC=38°,分别以AB、AC为边作两个等腰直角三角形ABD和ACE,∠BAD=∠CAE=90°.
(1)求∠DBC+∠ECB的度数;
(2)求证:DC=BE;
(3)若DC=6,求四边形BCED的面积.
【中考链接】
18、2018台湾11.(3分)如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )
A.115 B.120 C.125 D.130
19、2018湖北黄冈4.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为
A.50° B.70° C.75° D.80°
20、2018浙江丽水9.如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A. 55° B. 60° C. 65° D. 70°
21、2018浙江宁波23.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
参考答案
1、B 2、A 3、B 4、D 5、52.5°,52.5°或75°,30° 6、92°,44° 7、108°
9、B 10、C 11、A 12、67.5° 13、30 18、C 19、B 20、C.
8、解:∵AB=AD(已知),
∴∠B=∠ADB=(三角形内角和定理).
∵DE垂直平分AC(已知),
∴DA=DC(线段平分线上的到线段两个端点的距离相等).
∴∠C=∠DAC(等边对等角).
∵∠ADB=∠C+∠DAC(三角形的一个外角等于和
它不相邻两个内角的和)
∴∠C=∠DAC=
14、证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是腰AC和AB上的高,
∴∠BEC=∠CDB=90°(垂直定义).
在△BEC和△CDB中,
∵
∴△BEC≌△CDB(AAS)
∴CE=BD(全等三角形对应边相等).
15、解:∵AD,BE是△ABC的高,
∴∠ADB=∠ADC=∠BEC=90°(垂直定义)
∴∠1+∠C=90°,∠2+∠C=90°(直角三角形两个锐角互余)
∴∠1=∠2
在△BHD和△ACD中,
∵
∴△BHD≌△ACD(AAS)
∴BD=AD(全等三角形对应边相等).
∴∠ABD=∠DAB(等边对等角).
∵∠ABD+∠DAB=90°(直角三角形两锐角互余),
∴∠ABD=∠DAB =45°.
16、解:(1)①∵AF=AC,DB=DE,
∴△ABC和△DEF都是等腰三角形,
∴
,
同理
∵
∴
②由①可知
(2)、与存在同样的与∠1、∠2之间数量关系.
即
理由:所求的、、均与两个等腰三角形的两个底角之和为180°.
17、解答:(1)∵△ABD和△ACE均为等腰直角三角形,且∠BAD=∠CAE=90°,
∴∠ ABD=∠ACE=45°
∵∠BAC=38°,
∴∠ABC+∠ACB=180°-∠BAC =180°-38°=142°.
∴∠DBC+∠ECB=∠ABD+∠ABC+∠ACB+∠ACE
=45°+142°+45°=232°.
(2)∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC =∠CAE+∠BAC
即∠DAC=∠BAE.
在△DAC和△BAE中,
∵
∴△DAC≌△BAE(SAS).
∴DC=BE(全等三角形对应边相等).
(3)由(2)知△DAC≌△BAE,
∴∠ADC=∠ABE
∵∠1=∠2(对顶角相等)
∴∠3=∠BAD=90°.
∴DC⊥BE
∵DC=6,
∴BE =DC=6.
∴四边形BCED的面积=
21、【分析】(1)由题意可知:CD=CE,∠DCE=90°,由于∠ACB=90°,所以∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,所以∠ACD=∠BCE,从而可证明△ACD≌△BCE(SAS)
(2)由△ACD≌△BCE(SAS)可知:∠A=∠CBE=45°,BE=BF,从而可求出∠BEF的度数.
【解答】解:(1)由题意可知:CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB,
∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
∵
∴△ACD≌△BCE(SAS)
(2)∵∠ACB=90°,AC=BC,
∴∠A=45°,
由(1)可知:∠A=∠CBE=45°,
∵AD=BF,
∴BE=BF,
∴∠BEF=67.5°
【点评】本题考查全等三角形的判定与性质,解题的关键是熟练运用旋转的性质以及全等三角形的判定与性质,本题属于中等题型.
图1
例题1图
例题1图
第3题图
第4题图
第2题图
第7题图
第8题图
第13题图
第10题图
第14题图
第15题图
第16题图③
第16题图①
第16题图②
第17题图
第18题图
第20题图
第19题图
第21题图
第8题图
第14题图
第15题图
第16题图①
第16题图③
第16题图②
第17题图
第21题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
